转炉吹炼后期碳含量预报的改进指数模型

林文辉，焦树强，孙建坤，周凯啸，刘 敏，苏 醒，刘 青

1) 北京科技大学钢铁冶金新技术国家重点实验室，北京 100083 2) 江西新余钢铁集团有限公司技术中心，新余 338001 3) 江西新余钢铁集团有限公司第一炼钢厂，新余 338001

转炉炼钢作为当今世界最主要的炼钢方式，其产量占全球钢产量的70%以上，实现转炉自动炼钢控制也显得尤为重要.当前主流的转炉自动炼钢控制技术，根据检测手段的不同主要分为副枪技术和烟气分析技术等[1−10].由于烟气分析属于间接式测量，受到的干扰因素较多，其控制精度相对较低，国内外的转炉自动炼钢控制技术在很长一段时间内都是以副枪系统为主.但是，烟气分析具有连续测量的优点，更有利于实现转炉吹炼全过程的动态控制.近年来，随着烟气监测、网络通信、人工智能等技术的迅猛发展，转炉烟气分析吹炼控制误差大幅缩小，许多钢厂开始采用该项技术，逐步取代现有的副枪动态控制系统[11].意大利ILVA Taranto 公司[12]、加拿大 Dofasco 公司[13]，以及我国河钢唐钢公司[14]等国内外多家钢厂通过应用烟气分析技术，取得了较好的转炉终点控制效果.

烟气分析技术最早由法国钢铁工业研究院（IRSID）研发成功并申请专利[15]，常见的基于烟气分析技术的碳含量预报模型主要有碳积分模型、三次方模型和指数衰减模型.Dumont-Fillon等[16]和Meyer等[17]根据碳的质量守恒，采用对脱碳速率进行积分的方法推算熔池的总脱碳量，进而实现对熔池碳含量变化的连续预报.张贵玉等[18]通过分析转炉吹炼终点熔池碳含量与脱碳速率的对应关系，得到了终点碳含量对于脱碳速率的三次方拟合函数，从而提出用于预报终点碳含量的三次方模型.Glasgow等[19]研究了大量实际生产炉次的脱碳曲线，提出了基于脱碳氧效率的吹炼后期碳含量预报指数衰减模型，并引入了单点校正算法对预测结果进行修正；Uemura等[20]在此基础上将单点校正算法改进为多点校正算法；刘锟等[21]则通过对最大脱碳氧效率数值进行归一化处理，提高了不同炉次脱碳曲线的可比性.屠海[22]使用基于脱碳速率的指数衰减模型对吹炼后期碳含量进行预报，李南等[23]在此基础上引入了熔池混匀度[24]对烟气定碳模型参数进行了修正.

与积分模型和三次方模型相比，指数衰减模型能够更好地表征转炉吹炼后期熔池碳含量变化的一般性规律.但由于实际生产中每炉次的脱碳曲线都具有独特性，对于历史炉次脱碳曲线和当前炉次脱碳曲线特征的精准提取和有效利用，是决定指数衰减模型预报准确率的关键.本文利用国内某钢厂转炉冶炼数据对上述模型预测效果进行了对比，并对前人所建指数衰减模型进行了改进，提出了一种具有更好适应性和更高准确率的吹炼后期碳含量预报的改进指数模型.

1 转炉烟气曲线特点及定碳机理

转炉吹炼过程中，由氧枪喷出的高速氧气射流与炉内的高温液态铁水发生激烈的脱碳、燃烧等复杂的化学反应，最终得到液态的钢水、炉渣和气态的烟气等产物.其中，CO和CO2是转炉烟气最主要的组成部分，转炉吹炼过程典型的烟气曲线如图1所示.

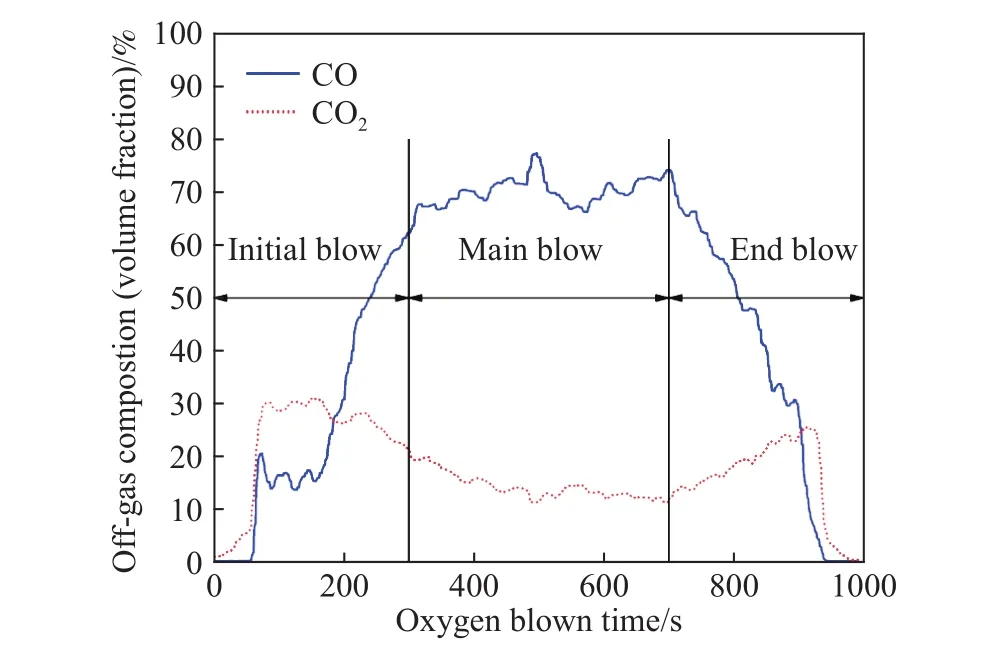
图1 转炉吹炼过程典型的烟气成分变化曲线Fig.1 Typical variation curve of BOF off-gas composition

根据经典脱碳三阶段理论，一般将转炉吹炼过程分为三个阶段，即吹炼初期、吹炼中期和吹炼后期.转炉吹炼初期（图中 300 s前），由于铁水中的Si、Mn元素优先被氧化，供入的氧气仅有一部分用于碳的氧化反应，烟气中的CO和CO2含量较低并呈逐渐升高趋势；随着Si、Mn含量的降低及熔池温度的升高，吹炼进入中期（图中300～700 s），碳氧反应剧烈发生，并在较长一段时间内保持相对稳定且较高的脱碳速率，该时期的脱碳速率主要受供氧强度控制；吹炼到后期（图中700 s以后）碳含量降低至临界含量后，熔池内碳的传质成为碳氧反应的限制性环节，导致脱碳速率迅速降低，烟气中的CO和CO2含量也随之降低.

根据转炉的烟气成分、烟气流量和吹氧流量等信息，运用式（1）、（2）计算出熔池的脱碳速率[16]和脱碳氧效率[19]：

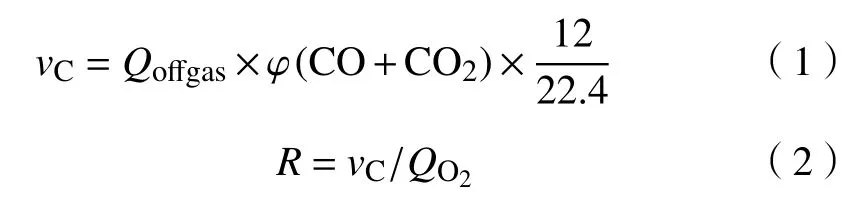
式中，vC为脱碳速率，kg·s−1；φ(CO+CO2)为烟气中CO和CO2的体积分数之和，%；Qoffgas为烟气流量，m3·s−1；R为脱碳氧效率，kg·m−3；QO2为即时氧气流量，m3·s−1.

其中，脱碳速率vC的定义是单位时间的熔池脱碳质量，受供氧强度的影响较大；而脱碳氧效率R的定义是单位体积氧气吹入量的熔池脱碳量，反映的是氧气的脱碳效率，受供氧强度的影响较小.

在转炉吹炼过程中，若能连续检测烟气的成分和流量，经过换算得到脱碳速率和脱碳氧效率，然后，建立相应的脱碳模型就能预报吹炼过程的熔池碳含量.而研究脱碳速率或脱碳氧效率与碳含量的对应关系，是建立精准的转炉碳含量预报模型的关键.

2 现有指数衰减模型算法分析

研究认为，转炉吹炼中期为高速脱碳期，碳氧反应主要受供氧强度影响，整个吹炼过程中脱碳氧效率的最大值出现在该时期内；进入转炉吹炼后期，当熔池碳含量降低至临界值以后，脱碳速率由熔池中碳的传质决定[25].此时，熔池碳含量与脱碳速率和脱碳氧效率均呈现较强的对应关系.根据前文所述，脱碳氧效率R与脱碳速率vC相比，其受供氧流量变化的影响更小，建模效果也更稳定，因此，基于脱碳氧效率R的指数衰减模型得到了更为普遍地研究和应用.

Glasgow等[19]研究了大量炉次的转炉吹炼后期脱碳曲线，发现脱碳氧效率与碳含量的关系可以用指数函数表示为：

式中，α为转炉的最大脱碳氧效率，kg·m−3； β 、γ为与脱碳氧效率相关的系数；R为实时脱碳氧效率，kg·m−3；C为熔池实时碳含量，%.

从式（3）和图2中可以看出，转炉吹炼后期的脱碳氧效率随熔池碳含量的降低呈指数衰减趋势.Glasgow等[19]提出的指数衰减模型具体算法为：首先，对历史炉次的脱碳数据进行处理，得到一条“历史脱碳曲线”；然后，使用当前炉次吹炼中期的最大脱碳氧效率对“历史脱碳曲线”中的参数进行替换，从而得到当前炉次吹炼后期的“参考脱碳曲线”；最后，计算脱碳氧效率从起始点0.95α到达校正点0.70α时“参考脱碳曲线”的脱碳量，并根据计算脱碳量与转炉实际脱碳量之间的偏差，对模型预报碳含量进行校正，进而得到当前炉次的“计算脱碳曲线”.Glasgow算法存在的问题主要有两个方面：一是由于采用单点校正的方法，如果校正点附近烟气曲线出现异常波动，会导致“计算脱碳曲线”的校正结果出现较大偏差；二是如果当前炉次的最大脱碳氧效率与“历史脱碳曲线”的偏差较大，会使“参考脱碳曲线”产生较大的偏离，同样会导致计算结果出现较大偏差.Uemura等[20]在Glasgow研究的基础上，将单点校正算法改进为多点校正算法，有效避免了单一校正点异常波动的影响；刘锟等[21]则进一步通过对脱碳氧效率进行归一化处理，将“历史脱碳曲线”和“参考脱碳曲线”的纵坐标统一到[0,1]之间，从而解决当前炉次与历史炉次偏差的问题.图3为这三种指数模型校正算法的示意图.

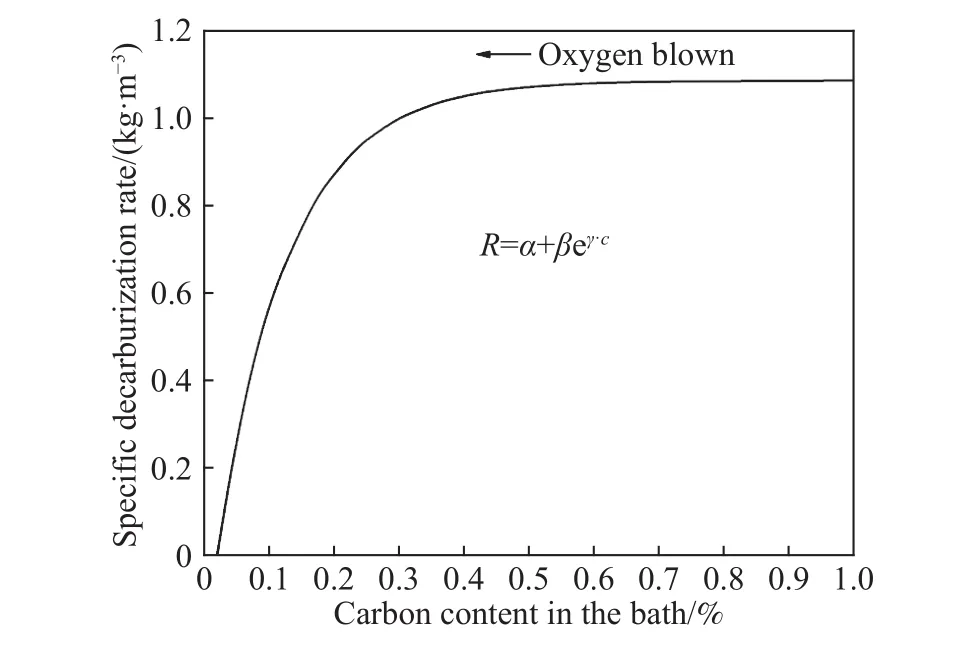
图2 转炉吹炼后期典型脱碳曲线Fig.2 Typical decarburization curve in the end-blowing stage of BOF

上述算法虽然取得了一定的改进效果，但是仍存在如下共同问题：（1）工业转炉的实际脱碳曲线并非严格意义上的标准指数衰减曲线，因此使用常规方法得到的“历史脱碳曲线”来表征吹炼后期的脱碳特性，仍然可能使模型预测结果存在较大的整体偏差；（2）每个炉次的“参考脱碳曲线”一旦确定后即不再变化，以此为基准通过校正算法得到的“计算脱碳曲线”，与“实际脱碳曲线”之间的偏差仍有待改进.因此，在实际应用中，得到更为合理的指数模型基准参数和对过程计算曲线进行动态校正是提高模型预测准确率的关键.

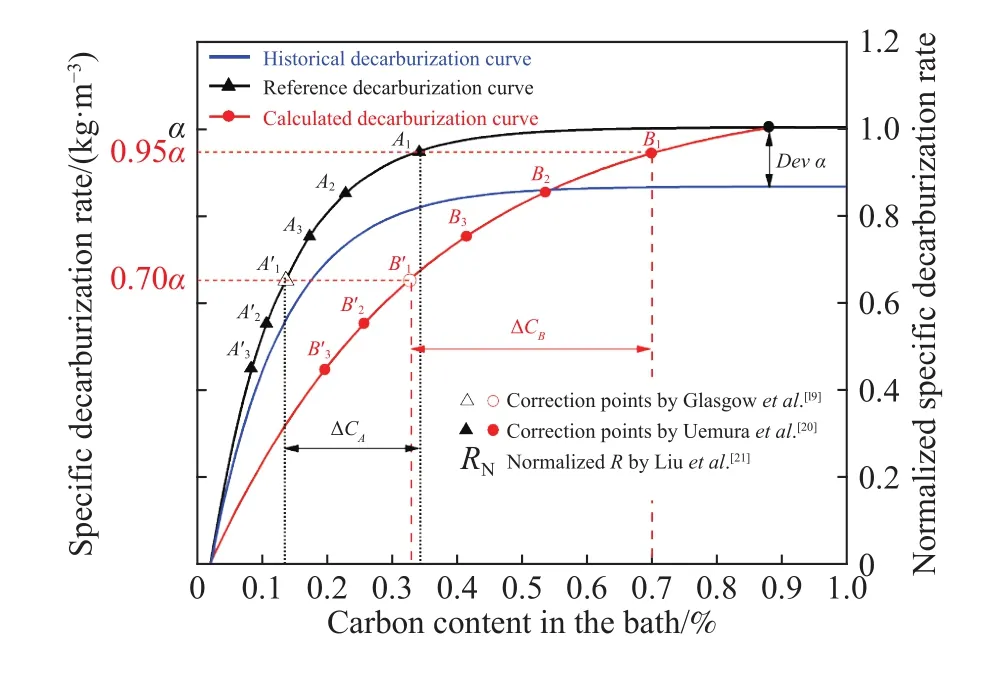
图3 三种指数衰减模型校正算法示意图Fig.3 Correction algorithm schematic of three exponential decay models

3 基于极限碳含量拟合与曲线同步更新的改进指数模型

3.1 极限碳含量拟合算法

当转炉吹氧脱碳量达到极限时，脱碳氧效率为零，即：

则：

式中，C0为熔池的极限碳含量，常规计算方法中通常取经验值0.02%，或通过热力学平衡计算获得.

由于实际转炉的工况条件与实验室完全不同，一般不可能达到完全的热力学平衡态[26]，因此，极限含量C0无论是取经验值或是取热力学平衡值，与实际情况相比都会存在一定的偏差，而且此偏差并不可控.文献[23]中，某钢种在平均工况下终点的极限碳含量平衡值为0.033%，采样炉次终点碳含量的实测值在0.035%～0.095%之间不等，平均终点碳含量为0.06%左右.本研究从最小化系统误差的角度出发，将C0也作为指数拟合参数之一，而非直接设定为某一固定值，从而有效控制由于C0设定方法导致的模型预测偏差.这样，根据大量历史炉次的实际脱碳氧效率和碳含量数据，通过指数拟合可以得到 α、、γ和C0的值，代入式（3）中就可得到比以往的研究法方法结果更贴近实际的“历史脱碳曲线”.

3.2 曲线同步更新算法

在得到上述“历史脱碳曲线”后，使用历史炉次最大脱碳氧效率的实际值 αH，对模型参数进行归一化处理，即RN=R/αH，βN= β/αH，γN=γ，代入式（3）可得：

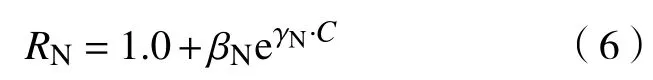
由此得到“归一化”的“历史脱碳曲线”.同理，使用当前炉的最大脱碳氧效率 αRef对“参考脱碳曲线”的模型参数进行归一化，得到“归一化”的“参考脱碳曲线”，然后，再根据吹炼至各等距离校正点时转炉的实际脱碳量与根据“参考脱碳曲线”计算得到的脱碳量之间的偏差，对该过程的计算脱碳曲线进行多点连续校正，如图4所示.

图4 等距离多点连续校正算法Fig.4 Algorithm of isometric multi-point correction

由图4可知，假设“参考脱碳曲线”（曲线A）和“计算脱碳曲线”（曲线B）分别经过点A1、A2、A3、A4···和点B1、B2、B3、B4···，其中A1点坐标为A2点坐标为B1点坐标为，B2点坐标为，代入式（6）可得：

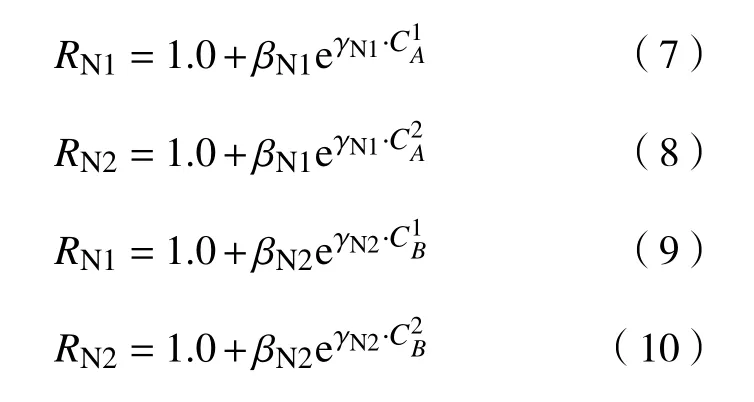
由于两条曲线都经过极限碳含量点(C0,0)，则有：

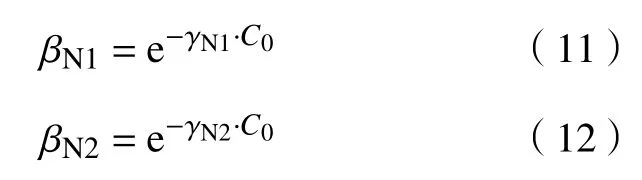
联立上式，可得：

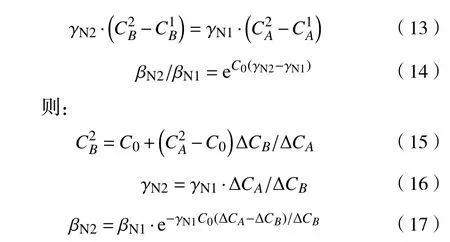
其中，∆CA为参考曲线脱碳量，可由已知条件求解、得出； ∆CB为实际脱碳量，根据实际的烟气成分和流量计算得出.

由此得到参数βN2、γN2和B1、B2点的碳含量、的值，将βN2、γN2代入式（6），得到经过校正的“计算脱碳曲线”，并将其作为下一次校正计算的“参考脱碳曲线”，每次计算都得到新的“计算脱碳曲线”参数和“参考脱碳曲线”参数，即“计算脱碳曲线”（曲线A）和“参考脱碳曲线”（曲线B）同步更新.

按上述方法取等距离的∆RN类推至点、A4···和B3、B4·，逐次计算得到点B3、B4···的碳含量、···，从而实现转炉熔池碳含量的连续预报，直至达到目标终点碳含量为止.

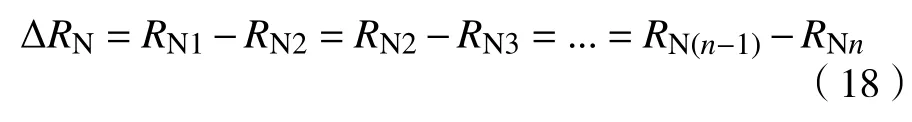
3.3 结果与讨论

本文建立的改进指数模型算法与之前的算法相比，主要有两点改进：（1）将熔池极限碳含量C0也作为指数拟合的参数之一，而非按以往研究方法直接将其设定为经验值或热力学平衡值等固定值，从而得到了更贴近实际的“历史脱碳曲线”及相应的模型参数，拟合效果如图5所示；（2）在“归一化+多点校正”方法的基础上，进一步提出了“参考脱碳曲线”与“计算脱碳曲线”同步更新的改进算法，既有效发挥了历史炉次曲线的参考作用，又充分利用了当前炉次的实际脱碳特征对指数模型的关键计算参数进行逐次修正，并同步更新“参考脱碳曲线”和“计算脱碳曲线”，从而有效减少了碳含量的计算偏差，改进算法的逐次计算曲线如图6所示.

由图5可以看出，采用本文方法拟合得到的“历史脱碳曲线”拟合优度更高，能够更好地表征转炉吹炼后期脱碳氧效率与熔池碳含量对应关系的共性规律，更充分地发挥了历史炉次数据的参考价值，从而得到更为合理的指数模型基准参数.从图6中可以看出，采用“曲线同步更新”算法，则更好地利用了当前炉次实际脱碳曲线的参考价值，使碳含量计算值与实际值的偏差随着曲线的逐次计算更新而逐次减小，模型的准确率进一步提高.

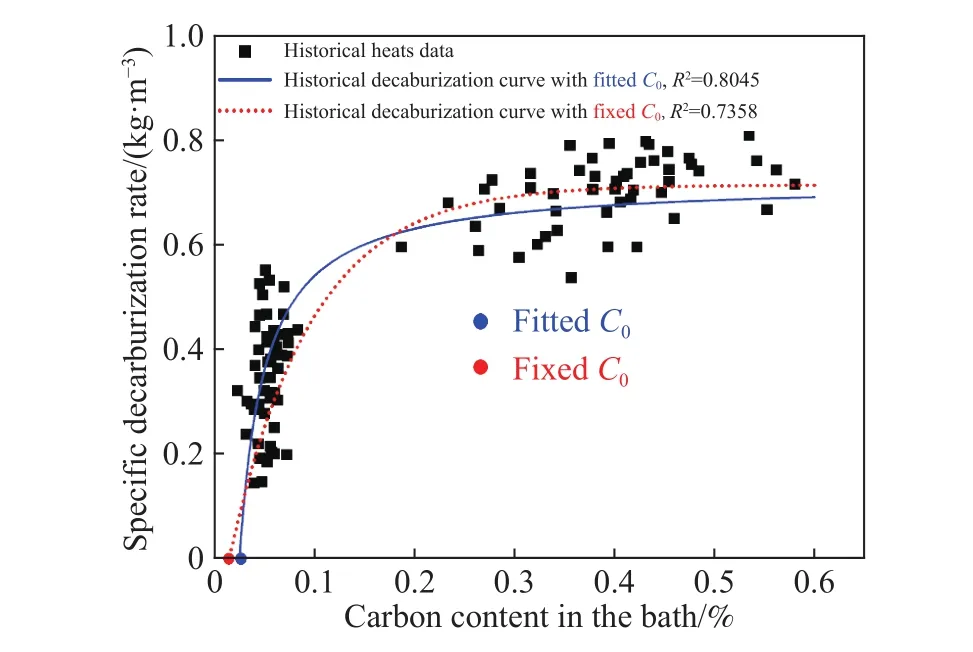
图5 采用不同 C0 设定方法得到的历史脱碳曲线Fig.5 Historical decarburization curves with different C0 values

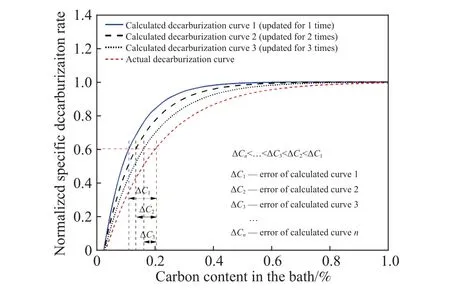
图6 改进算法的计算脱碳曲线Fig.6 Calculated decarburization curves using the improved algorithm

采用某转炉炼钢厂实际生产数据对本文建立的改进指数模型进行验证，其中10炉详细数据见表1，从表1中可以看出采用本文提出的改进算法得到的结果整体上符合误差逐次减小的规律.

采用某钢厂80炉同一钢种的生产数据对前文所述几类模型的预测效果进行了验证，其中表2为终点碳含量预测误差ΔC≤±0.02%的命中率指标，预测误差的具体分布情况见图7.从表2和图7可以看出：“极限碳含量拟合”、“曲线同步更新”两种修正方法均能使预测模型命中率提高2%～3%左右；“极限碳含量拟合”算法对模型预测值相对于实际值的整体偏移有较明显的修正效果，“曲线同步更新”算法则更有利于提高模型在较小误差范围内的命中率；与其他模型相比，本文提出的两种修正方法综合的改进指数模型命中率更高，达到了90%.

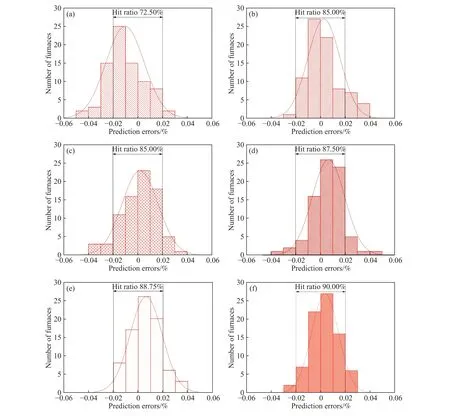
图7 不同模型预测误差分布.（a）积分模型；（b）三次方模型；（c）固定 C0 且曲线不更新的指数模型；（d）固定 C0 且曲线更新的指数模型；（e）拟合C0且曲线不更新的指数模型；（f）拟合C0且曲线更新的指数模型Fig.7 Prediction error distribution of the different models: (a) integral model; (b) cubic model; (c) exponential model with fixed C0 but without updated curve; (d) exponential model with fixed C0 and updated curve; (e) exponential model with fitted C0 but without updated curve; (f) exponential model with fitted C0 and updated curve

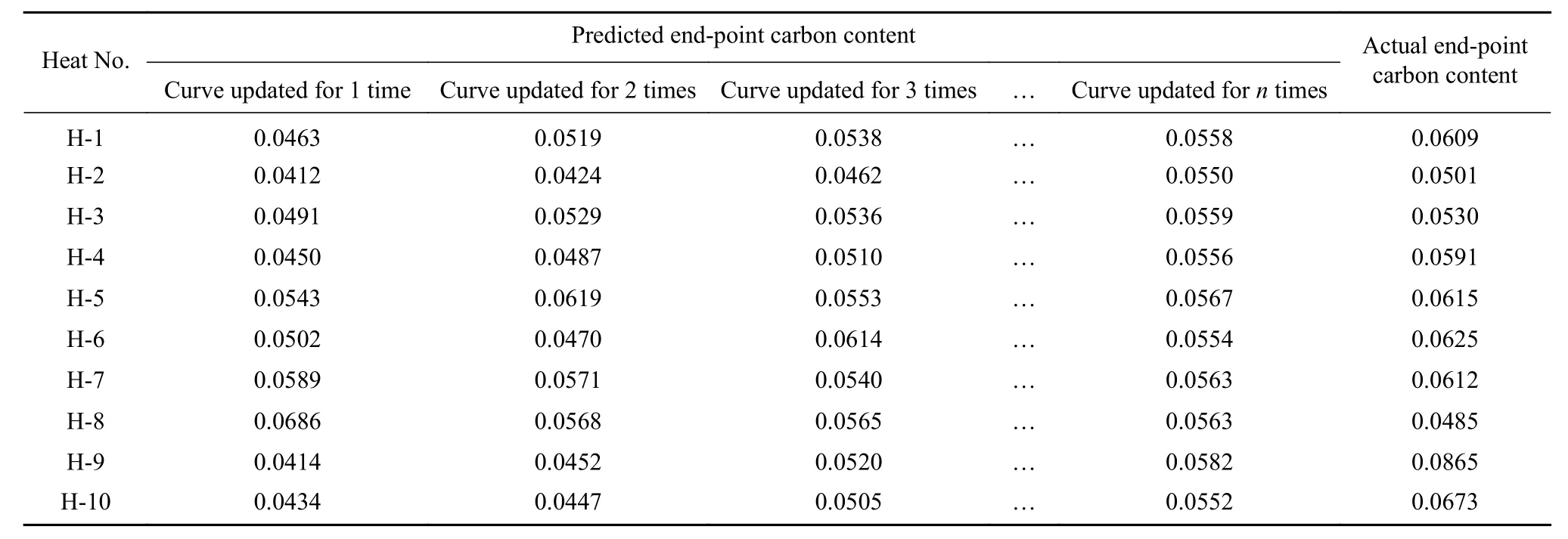
表1 “极限碳含量拟合+曲线同步更新”算法改进模型验证数据Table 1 Validation of proposed model based on improved algorithm %

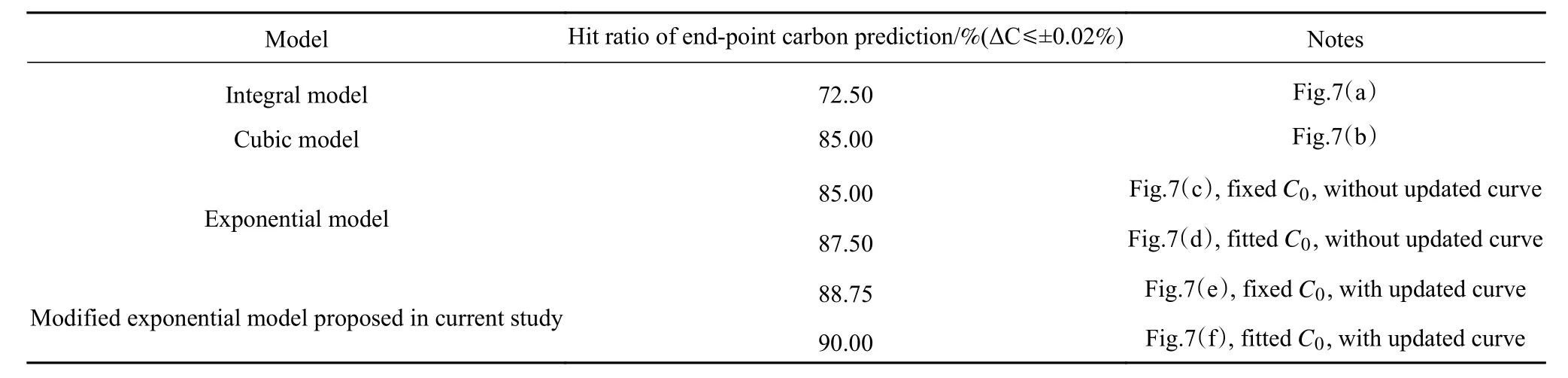
表2 几种模型终点碳含量预测命中率Table 2 Hit ratios of the different models

4 结论

（1）综合分析了转炉碳含量预测常用的碳积分模型、指数模型和三次方模型的特点，指数模型更适合用于表征转炉吹炼后期熔池碳含量变化的共性规律，采用实际生产数据对各模型算法进行了验证，结果表明指数模型具有更好的适应性和准确性.

（2）考虑实际工况的影响，将熔池极限碳含量C0也作为指数模型的拟合参数之一，而非直接设定为经验值或由热力学平衡计算得到的固定值，可以获得更贴近实际的“历史脱碳曲线”及对应的指数模型特征参数.

（3）采用“参考脱碳曲线”与“计算脱碳曲线”同步更新的改进算法，既有效发挥了历史炉次脱碳曲线的参考价值，又充分利用了当前炉次实际脱碳曲线的特征，从而获得更高的计算准确度，本文提出的改进指数模型终点碳预测误差在±0.02%范围内的命中率达到90%.