采用三角形原理改善拱桥的动力特性

谢肖礼, 徐 红, 邓俨峰, 戴纳新

(1.广西大学 土木建筑工程学院,广西 南宁 530004; 2.南华大学 土木工程学院,湖南 衡阳 421001)

拱梁固结拱桥属于梁拱组合体系桥梁结构形式[1],具有结构轻巧、跨度大、外部无水平推力等特点,广泛适用于大跨度公路桥梁和铁路桥梁[2-5]。但随着结构形式的多样化以及车辆荷载不断增大,车辆荷载引起的桥梁振动问题逐渐突出[6-8]。对于传统的拱梁固结拱桥[9-12],虽然可以做到无推力和约束梁端竖向转角,但随着跨度和桥宽的增加,传统的拱梁固结拱桥在荷载作用下很容易产生剪切和弯曲变形,从而导致其力学性能(刚度、动力、稳定、强度承载力、疲劳)快速下降,其结构的刚度和动力性能远不能满足大跨度公路桥梁、重载铁路桥梁的行车要求[13]。实际工程设计中,一般通过优化横撑布置、增加横撑数量、增大拱肋内倾角等方法来增加拱的横向整体刚度[13],也可采用斜向吊杆提高结构的面内刚度,但其对于结构的面外刚度贡献不大[14]。为解决上述问题,本文引入三角形稳定性理念,将传统拱桥改造成具有更优力学性能的新型拱桥,来改善拱梁固结拱桥的动力特性。本文介绍了其结构形式以及力学原理,利用有限元软件分析了新型拱桥结构形式的自振频率与振型特征,与传统的拱梁固结拱桥作对比,并研究了不同宽跨比对新型拱桥结构自振频率的影响。

1 采用三角形原理改善拱桥动力特性

为改善拱梁固结拱桥的动力特性,本文提出一种新的结构形式对传统的拱梁固结拱桥(以下简称“对比拱桥”)进行改造,其主要由拱肋、主梁、V型撑、柔性吊杆及横撑组成,以下简称“本文拱桥”,具体布置如图1所示。

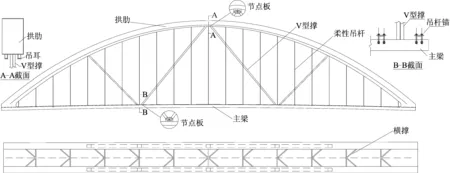
图1 本文拱桥整体及局部构造图

(1) 引入三角形理念约束拱肋及主梁。三角形结构受节点力的作用,因而处于轴向变形的状态,三角形稳定性也基于此原理。桥梁结构主要承受移动荷载作用,这样就会使以上所形成的三角形受非节点力作用,导致三角形的稳定性有所下降。为了增加对主梁的弹性约束,提高主梁的线刚度以减少弯曲变形,需在拱肋和主梁之间设置足够密的柔性吊杆,使多个三角形均能保证有良好的稳定性。根据以上原理,本文拱桥在主梁与每条拱肋间增设2个V型撑,全桥共设置4个V型撑,使其与拱和梁段构成若干个三角形结构,从而对主梁与拱肋进行有效约束,提高结构的整体刚度。与传统拱梁固结拱桥不同的是,本文拱桥的拱肋与主梁得到更好的相互约束,整体刚度大幅度提高。

(2) 结合位移包络图合理布置三角形角点。拱肋和主梁的截面在移动荷载以及恒载作用下的位移包络图反映了位移的极限值,由此可知结构的薄弱处,从而可以合理布置三角形角点。

主梁和拱肋的位移包络图形态分别如图2、图3所示。

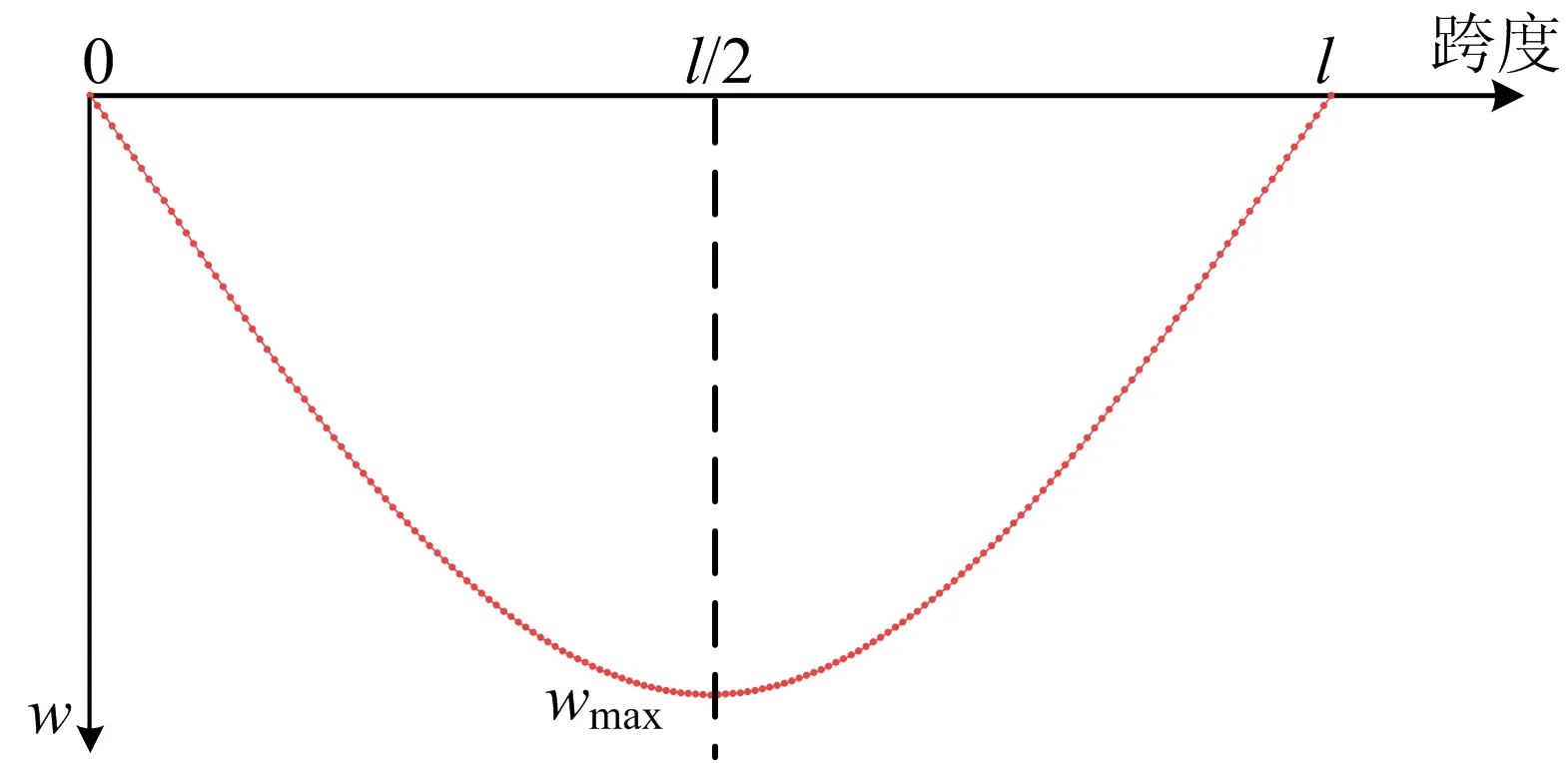
图2 恒载下主梁位移包络图

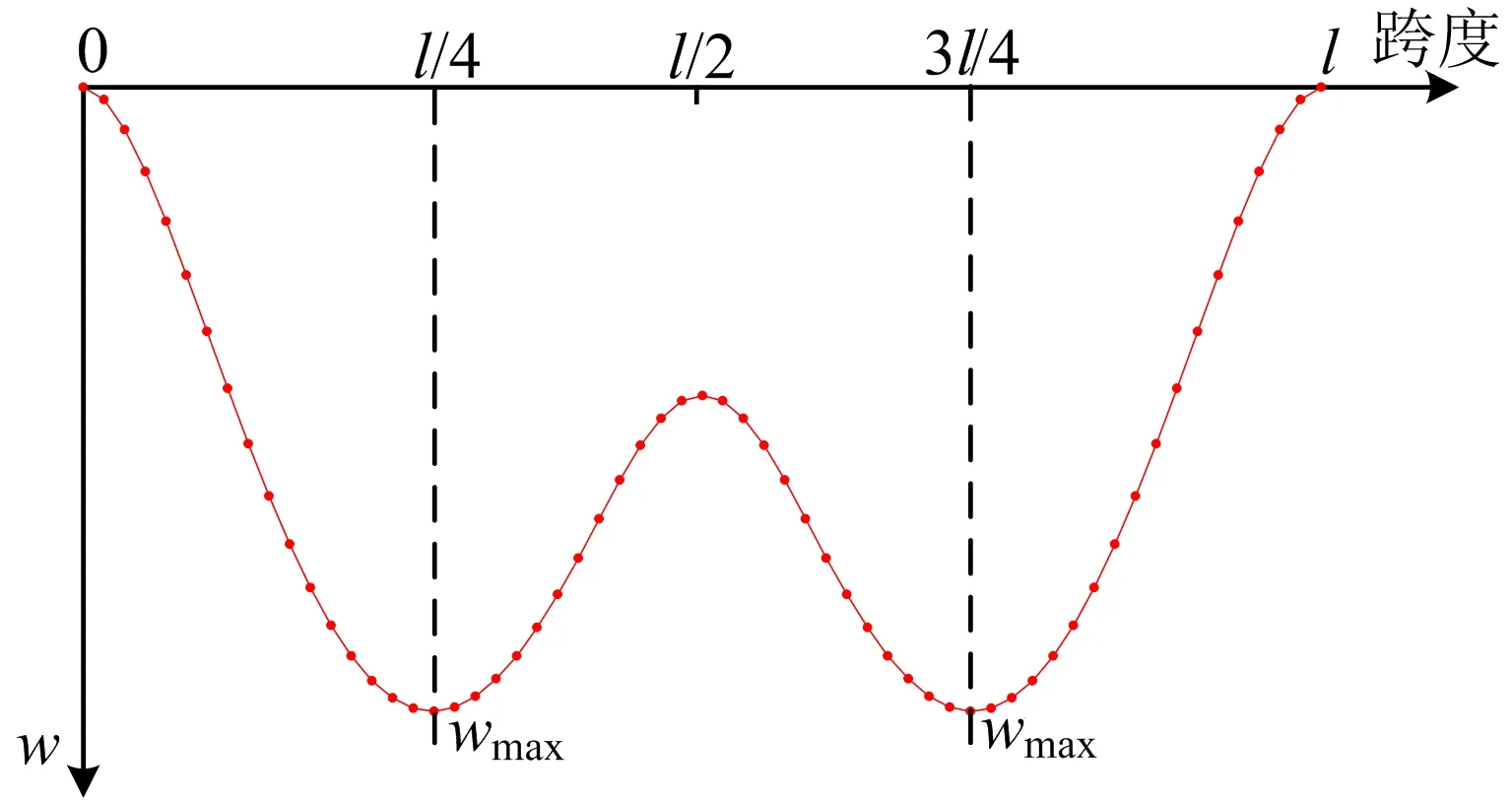
图3 移动荷载下拱肋位移包络图

图2、图3中w为竖向挠度,l为桥梁跨径。由图2、图3可知,位移极值出现在4分点附近及2分点处。结合位移包络图,三角形角点布置的方式有:① 尽可能通过角点分别对拱肋和主梁进行均匀约束,从而达到既提高它们的线刚度又使其受力均匀的目的;② 保证有约束点落在拱肋或主梁位移包络图的极值点附近,使得主梁或拱肋的薄弱点处得到加强,改善结构的力学性能。

(3) 控制V型撑个数平衡刚度与温度响应。增加的V型撑并非受节点力作用,增设的数量过多会使结构超静定次数增加。由于温度变化引起拱轴线的伸长或收缩,这使得拱肋任意截面产生附加内力,由温度变化作用下n次超静定结构的力法方程可知,第i个方程的一般形式为:

(1)

其中,Xj为第j个约束力;δij为单位力Xj=1引起的沿Xi方向的位移,称为柔度系数;Δit为结构在温度变化作用下沿Xi方向的位移;Δi为原结构沿Xi方向的位移。从(1)式可以看出,n次超静定结构有n个多余约束,每个多余约束对应一个未知的约束力X。温度变化使拱肋任意截面产生的附加弯矩为:

(2)

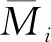
拱肋截面的剪力和轴力也同理计算。

由(1)式、(2)式可知,增加的超静定次数越多,在温度变化下,引起结构的附加内力就越大,而当增加的V型撑较少时,若未能约束拱肋的4分点和2分点的薄弱处,则会造成结构刚度的改善效果不明显。因此,控制好V型撑的个数可以让刚度与温度达到较为合理的状态。根据上述分析,本文拱桥设置2个V型撑。

(4) V型结构与主梁的夹角要适中。本文拱桥的V型撑与主梁的夹角不宜过大或过小。为了保持三角形的良好受力特性并且保证三角形底边有合适的线刚度,同时考虑V型撑与主梁的构造连接,经过有限元计算可知,该夹角在30°～60°范围较为合理。

(5) 连续布置三角形提高体系抗变形能力。本文拱桥增设连续三角形可以大幅提高结构的抗变形能力。这是由于连续三角结构每边所承受的力以轴力为主,主要产生轴向变形;若布置不连续的三角形结构,则会使主梁在剪力作用下发生较大的弯曲变形。三角形结构不连续布置示意图如图4所示。

从图4中三角形结构分离出梁段BB′,由节点B平衡可知,在BB′段产生了剪力,于是在BB′梁段就会产生弯曲变形,因此,所布置的三角形必须保证连续以减少结构的变形。

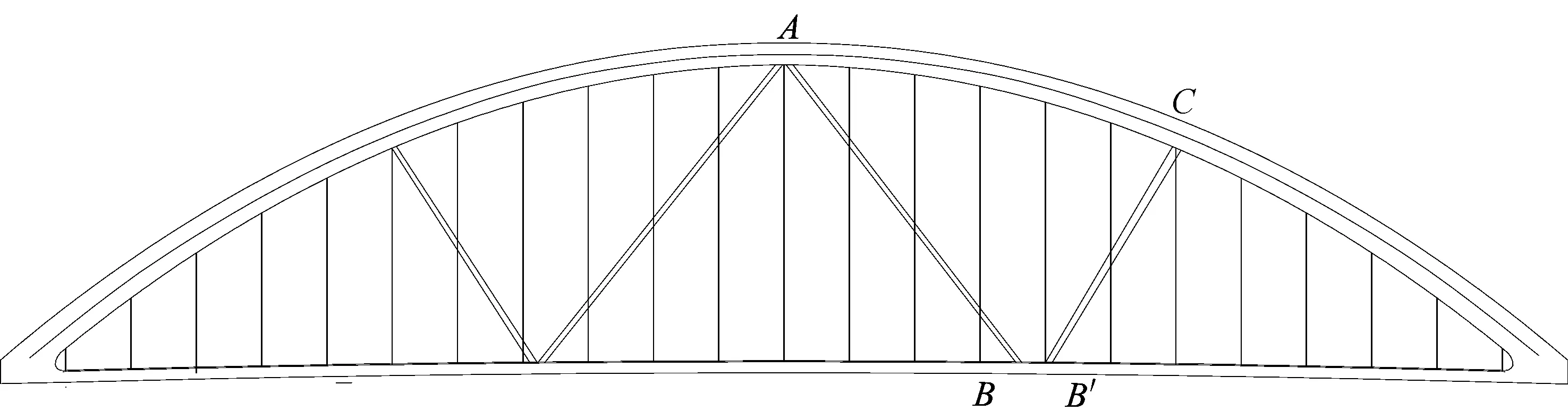
图4 三角形结构不连续布置示意图

(6) 体系适时转换以保持拱结构的优越性。本文拱桥按普通拱桥成桥后(即上完一期、二期恒载),再安装V型撑,此时保留了普通体系的拱肋在恒载状态下的优点。以完成的普通拱桥作为施工平台,安装V型撑较为容易,等体系转换完成后,V型撑与拱肋及主梁节段所构成的三角形结构参与抵抗移动荷载及其他荷载,从而达到减少结构在移动荷载作用下变形的目的。

2 有限元模型

本文以288 m跨径为例,荷载等级为公路Ⅰ级。本文拱桥和对比拱桥矢跨比均为1/4.8,拱轴系数为1.28,拱肋采用钢箱结构,拱顶到拱脚变截面高4～6 m,等截面宽为2 m;拱肋钢箱顶板厚32 mm,底板厚28 mm,腹板厚18 mm。桥面宽为14 m，两片拱肋间距为14 m,拱肋之间设置多道K型撑以提高侧向稳定性[15-16]。本文拱桥设计图如图5所示(单位为mm)。为保证结构用钢量相同,从对比拱桥拱肋中减少500 t用钢量作为V型撑材料用量,其余结构用钢量相同。本算例中,本文拱桥和对比拱桥用钢量均约为4 855 t,各构件的详细参数和材料用量见表1所列。本文拱桥的拱肋、主梁、横撑、V型撑采用钢结构,吊杆采用钢绞线,钢与钢丝弹性模量均为210 GPa,泊松比均为0.3,密度均为7 850 kg/m3。本文拱桥的拱肋和V型撑的截面参数分别如图6、图7所示(单位为mm)。边界条件处理为:拱梁固接,下设弹性支座,整桥简支在桥台上。为保证构件的局部稳定性,本文依据文献[17]给拱肋设置纵向加劲肋、横隔板。

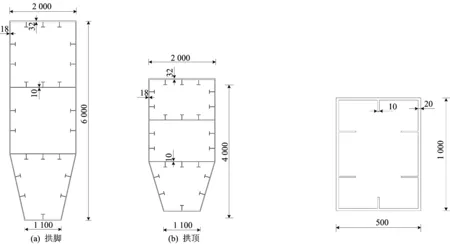
图6 本文拱桥拱肋截面 图7 V型撑截面

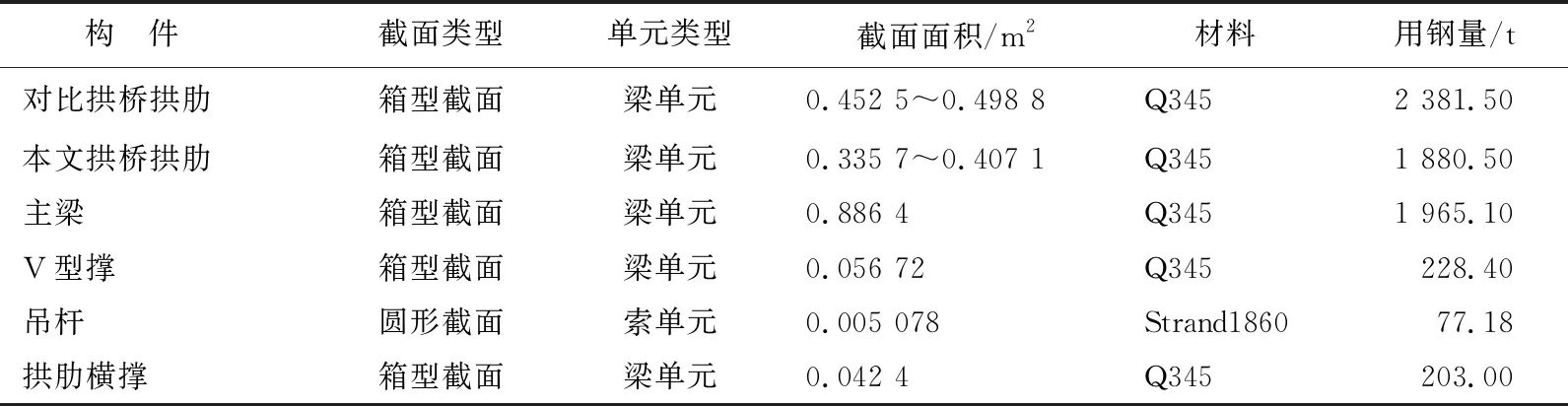
表1 本文拱桥与对比拱桥构件设计截面参数

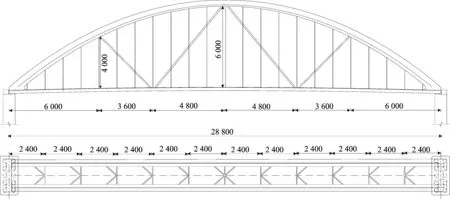
图5 本文拱桥设计图

本文拱桥和对比拱桥的成桥状态有限元计算模型如图8、图9所示。

图8 本文拱桥有限元模型 图9 对比拱桥有限元模型

3 自振特性分析

3.1 本文拱桥自振频率分析

利用有限元软件Midas/Civil,分别对本文拱桥和对比拱桥进行自振频率分析。采用Lanczos法计算本文拱桥和对比拱桥的前10阶自振频率和自振振型,探讨本文拱桥的自振频率变化规律,并与同等条件下的对比拱桥进行对比分析。

本文拱桥和对比拱桥前10阶自振频率计算结果见表2所列,前5阶自振振型如图10所示。

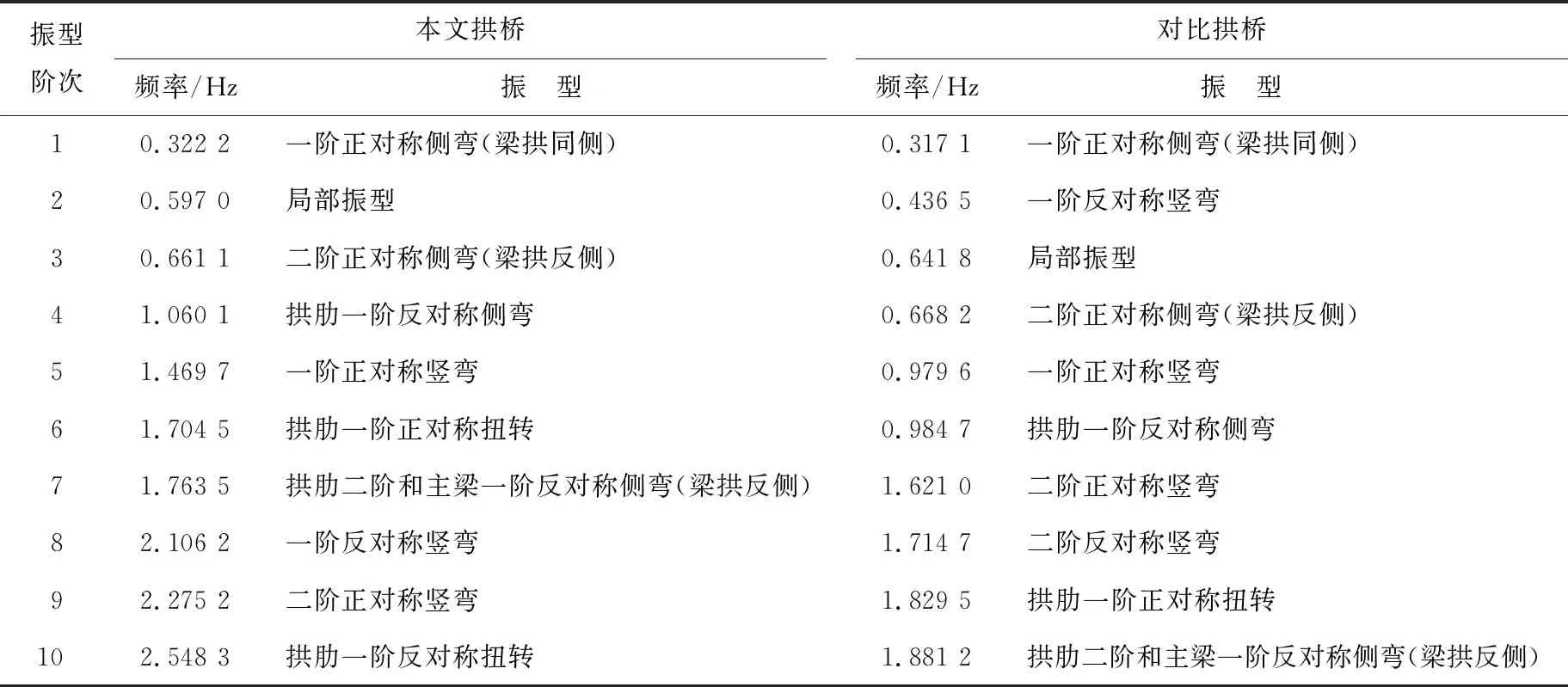
表2 本文拱桥和对比拱桥前1阶自振频率计算结果

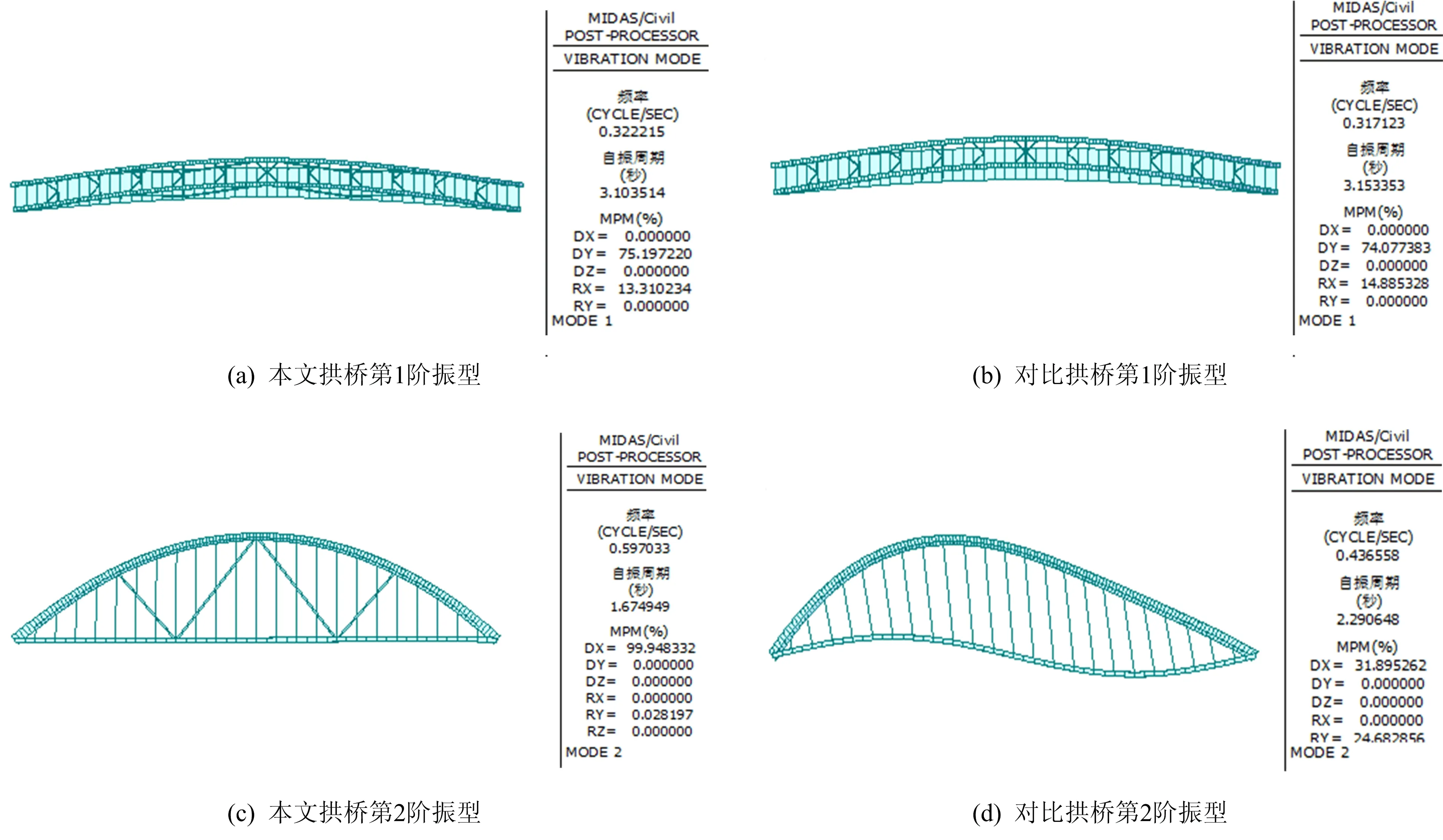
图10 本文拱桥和对比拱桥前5阶振型图

由表2可知,本文拱桥一阶面外自振频率为0.322 2,而对比拱桥的面外自振频率为0.317 1。由此可见,在用钢量相同的情况下本文拱桥的一阶面外自振频率比对比拱桥提高了1.5%,说明加V型撑后本文拱桥并未降低面外基频,保持了传统拱梁固结拱桥的特性。本文拱桥一阶面内的自振频率为1.469 7,而对比拱桥的一阶面内自振频率为0.436 5,与对比拱桥相比提高3.3倍,说明加V型撑能够显著提高拱桥的面内刚度,大幅提高面内基频。

从图10可以看出,本文拱桥和对比拱桥首次发生面外振动均在第1阶,随着自振频率阶数增加,本文拱桥首次发生面内振动在第5阶,而对比拱桥首次发生面内振动在第2阶,因而V型撑能够大幅提高拱梁固结拱桥的面内刚度,延迟面内振动发生的阶数。

另外,有限元分析表明,本文拱桥的拱肋在恒载+活载下的组合应力小于对比拱桥,说明加V型撑后,本文拱桥不仅受力性能得到改善,并且动力特性也得到大幅提升。

3.2 宽跨比对本文拱桥自振频率的影响

(1) 不同桥面宽下宽跨比对自振频率的影响。以288 m跨径为例,建立5种宽跨比下的有限元动力模型,其桥面宽为8、14、20、26、32 m,对应的宽跨比分别为0.03、0.05、0.07、0.09、0.11,其他参数保持一致;并在相同用钢量的情况下与相同宽跨比下的对比拱桥进行对比分析。

本文拱桥5种桥面宽下前5阶自振频率计算结果见表3所列。

宽跨比对本文拱桥和对比拱桥面内和面外基频的影响趋势分别如图11、图12所示。

由表3、图11、图12可知,本文拱桥在同一跨径不同桥面宽下均表现良好的动力性能,其面内和面外的基频均高于对比拱桥。

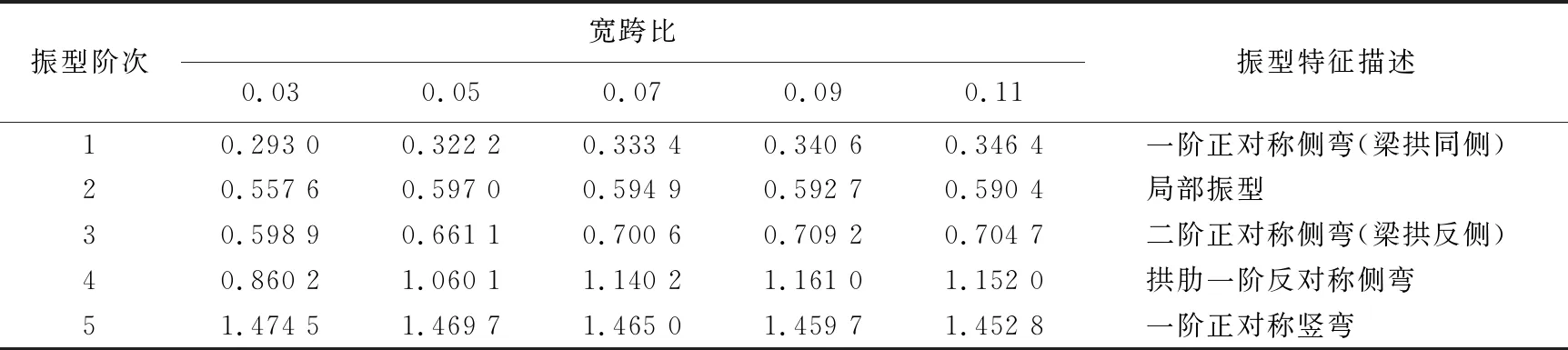
表3 本文拱桥不同桥面宽下前5阶自振频率 Hz

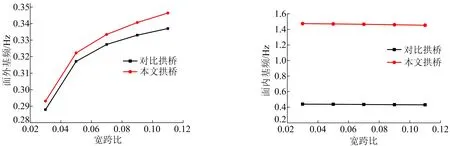
图11 不同桥面宽下宽跨比对面外基频的影响 图12 不同桥面宽下宽跨比对面内基频的影响

从图11可以看出,随着宽跨比增大,本文拱桥和对比拱桥的面外基频曲线增长,说明V型撑的设置并未改变宽跨比对传统拱桥面外基频的影响趋势,并且宽跨比增大时,本文拱桥面外基频比对比拱桥提高的幅度更大。从图12可以看出,随着宽跨比增大,本文拱桥和对比拱桥的面内基频曲线下降,面内基频下降的幅度较小,但本文拱桥的面内基频是对比拱桥面内基频的2～3倍趋势保持不变。

(2) 不同跨径下宽跨比对自振频率的影响。以桥面宽为14 m为例,建立5种宽跨比下的有限元动力模型,其计算跨径为80、100、120、140、160 m,对应的宽跨比分别为0.17、0.14、0.12、0.10、0.08,其他参数保持一致;并在相同用钢量的情况下与相同宽跨比下的对比拱桥进行对比分析。本文拱桥5种跨径下前5阶自振频率计算结果见表4所列,宽跨比对本文拱桥和对比拱桥面内和面外基频的影响趋势分别如图13、图14所示。

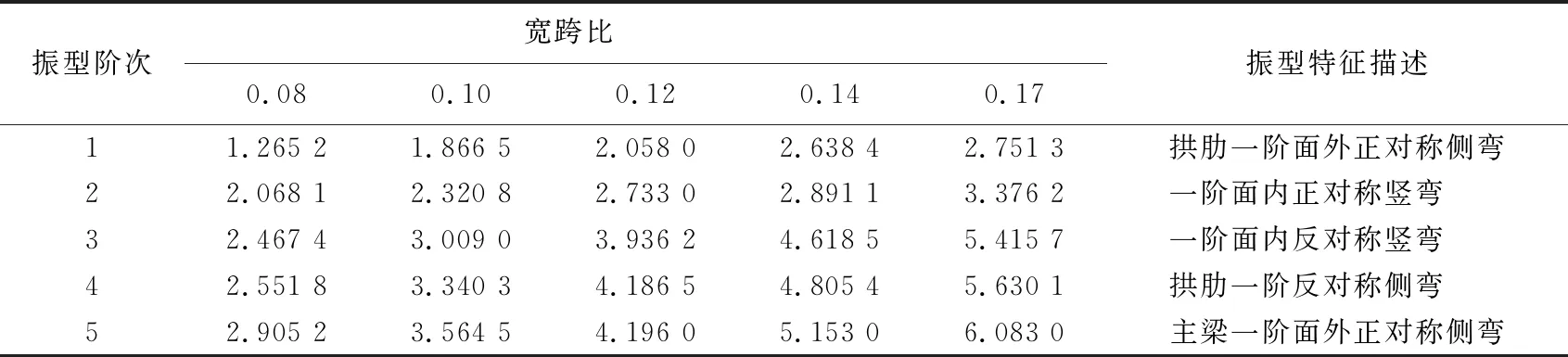
表4 本文拱桥不同跨径下前5阶自振频率Hz

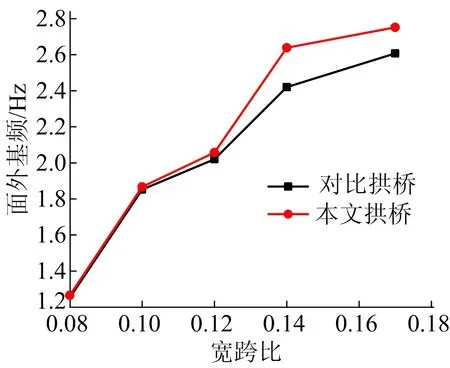
图13 不同跨径下宽跨比对面外基频的影响

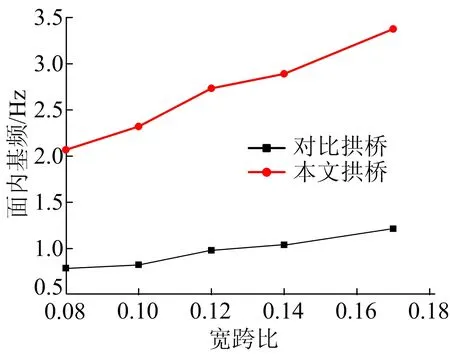
图14 不同跨径下宽跨比对面内基频的影响

由表4、图13、图14可知,在同一桥面宽不同跨径下本文拱桥和对比拱桥的面内和面外基频变化趋势相同。从图13可以看出,在大跨径下即宽跨比较小时,本文拱桥和对比拱桥的面外基频大致相同,随着宽跨比增大,本文拱桥面外基频增长率大于对比拱桥。

从图14可以看出,随着宽跨比增大,本文拱桥和对比拱桥的面内基频曲线递增,但本文拱桥的面内基频曲线一直位于对比拱桥的上方,并且面内基频是对比拱桥的2～3倍。由图13、图14可知,随着宽跨比增大,本文拱桥面外基频的增长幅度大于面内基频的增长幅度。

4 结 论

(1) 本文采用三角形原理来改善拱梁固结拱桥的动力特性,即在传统的拱肋和主梁间加入2个V型撑,使其与拱肋和主梁构成若干个三角形结构,从而对主梁与拱肋进行有效约束,提高结构的整体刚度。

(2) 对本文拱桥的自振特性分析可知,在结构用钢量相同的情况下,V型撑能够大幅提高结构面内刚度,与传统的拱梁固结拱桥相比,本文拱桥面内自振频率得到提高,面内基频提升至传统拱桥的3倍左右,面外自振频率并未降低,因而V型撑能够改善结构的刚度和自振频率。

(3) 对本文拱桥在不同宽跨比下的自振频率分析可知,本文拱桥仍然表现良好的动力性能,其性能远优于传统的拱梁固结拱桥。宽跨比较小时,本文拱桥和传统拱桥面外基频相差较小,当宽跨比较大时,本文拱桥面外基频增长的幅度较大,说明V型撑在大宽跨比下可以显著提高结构的面外基频;并且在各宽跨比下本文拱桥的面内基频均远高于对比拱桥,V型撑可以大幅提高结构的面内基频。

因此本文提出的这种新结构形式对于改善传统拱梁固结拱桥动力特性是显著和有效的。