糙条消能工对弯道水流动能调整试验研究

张红红，牧振伟，李凡琦，贾萍阳

(新疆农业大学 水利与土木工程学院，新疆 乌鲁木齐 830052)

1 研究背景

弯道溢洪道可充分利用地形并节省工程量，但由于带有转角，当水流进入弯道时，会出现一些不同于直段河道水流的水力现象，弯道的存在，会导致弯道环流、横向水面高差、横向流速分布不均等问题[1]。本文所采用的糙条消能工基于已有的工程实例新疆“635”工程进行研究说明，新疆“635”工程的溢洪道弯道处正是采用糙条进行消能导流。对于弯段溢洪道所存在的问题，杨飞等[2]、王青等[3]、严培等[4]分别通过采用垂向基于谱方法的简化三维模型、基于Flow-3D方法、MIKE3软件等对弯道水流进行了数值模拟，并进行模型验证；董玉莲[5]介绍了水面横比降、弯道环流、急流冲击波的计算公式，并提出了削减弯道急流冲击波的措施；王田田等[6]、昌子多等[7]、赵经华等[8]、魏祖涛等[9]、孙一等[10]对弯道水流进行了水流特性试验，提出了改善弯道水流流态的工程措施，认为糙条作为一种新型消能工有着重要的研究意义；李锦艳等[11-12]、孙德旭等[13]研究了糙条对多弯段溢洪道的消能导流作用并加设导流墩与糙条联合消能，验证了糙条是有效的消能措施；高学平等[14]、李凡琦等[15-16]提出并细化了影响弯道水流的因素，这为本文试验分析指标提供了重要依据；张红红等[17]等基于量纲分析方法，提出了一种糙条高度的计算方法，这也是本文设计试验的重要依据。

针对弯段溢洪道所存在的问题，本文着重研究对弯道水流的动能调整，通过在弯段溢洪道布置不同型式的糙条，借助物理模型试验的研究方法，来解决弯道段溢洪道断面动能分布不均的问题，以达到较快使水流动能在横断面上重新均匀分配、缩短纵向流速分布调整的距离、改善水流流态的效果。

2 模型试验概况

2.1 模型装置

试验采用自循环式供水系统，主要由上游水池区、模型试验区、量水堰区、下游水池区、水泵区和供水管道区组成。上游水池区含稳流前池装置；模型试验区用于放置溢洪道模型，是试验的核心区域；量水堰区用于放置模型量水堰，可进行流量校核，对流量有调整和控制的作用；水泵区用于装置水泵，可将下游水池中的水抽送至上游水池中；供水管道区用于安装供水管，以形成完整的自循环式供水系统。试验的模型装置系统平面结构如图1所示。

图1 模型装置系统平面结构示意图

试验的核心部分为模型试验区，该试验区模型主体即溢洪道由亚克力有机玻璃板制成，断面全程为矩形，溢洪道模型宽度为等宽0.5 m，坡度i=0.025。模型主体由进口直段、弯道段(布置糙条区)、出口调整段3部分组成。进口直段长0.6 m，经试验验证，能够使水流在进入弯段前保持平稳状态，便于试验研究和数据测量，满足试验要求。弯道段转角为60°，曲率半径采用0.85 m，主要用于布置糙条，糙条的布置参数不同，对水流的消能作用则不同。出口直段长1.4 m，经试验验证，满足弯道水流流出弯道后的调整距离。模型主体结构平面布置如图2所示。

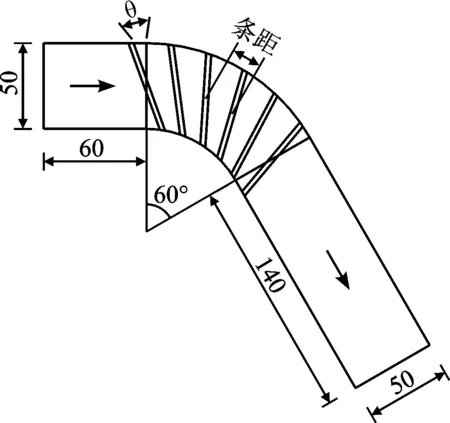
图2 模型主体结构平面布置示意图(单位：cm)

2.2 试验工况设计

试验采用同一流量和糙条宽度，将糙条的高度和条距设为变量参数。流量Q设置为22.5 L/s，糙条宽度b设置为2.7 cm。在选取糙条高度hz时，采用凹凸面高度比值为2∶1的3种不同高度，分别为1.6～0.8、2.0～1.0、2.4～1.2 cm；条距采用14.0、18.0、22.0 cm。糙条纵断面图如图3所示。

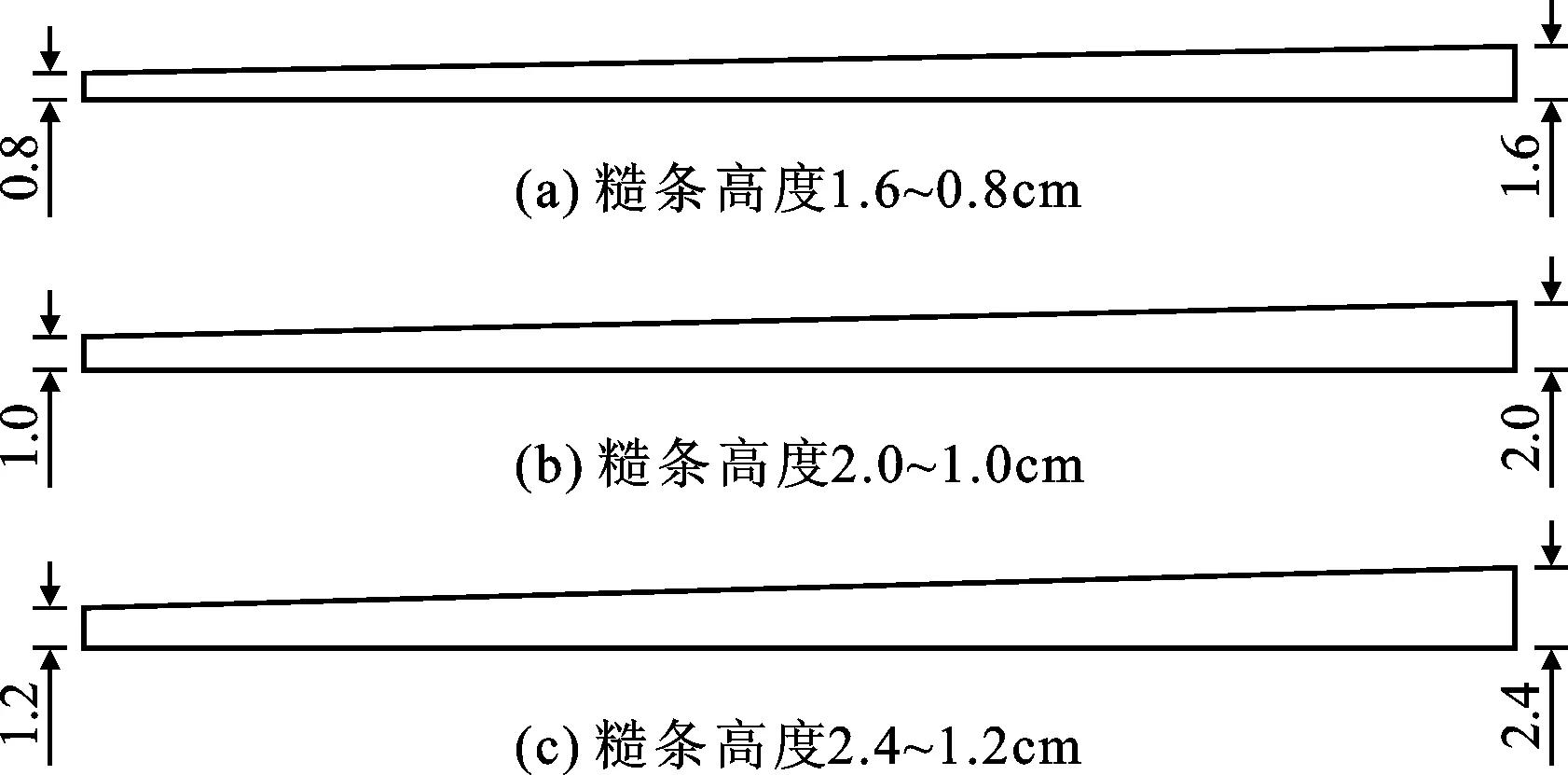
图3 3种高度糙条的纵断面图

试验先进行1组无糙条工况下的数据量测，以便于与有糙条的试验工况进行对比。其次，进行5组有糙条工况的试验：先保持糙条的高度为1.6～0.8 cm不变，改变条距，进行3组试验，由该3组试验得出的最佳条距为18.0 cm，将其设置为定值，改变糙条高度，进行2组试验。具体的试验工况及其设定参数如表1所示。

表1 试验工况及其设定参数

2.3 数据量测

试验数据量测断面根据模型的3个主要组成部分进行布置，共分为50个断面。进口直段每6cm取1个断面，共10个断面。弯道段每3°取1个断面，共20个断面。出口调整段每7 cm取1个断面，共20个断面。模型量测断面布置图如图4所示。

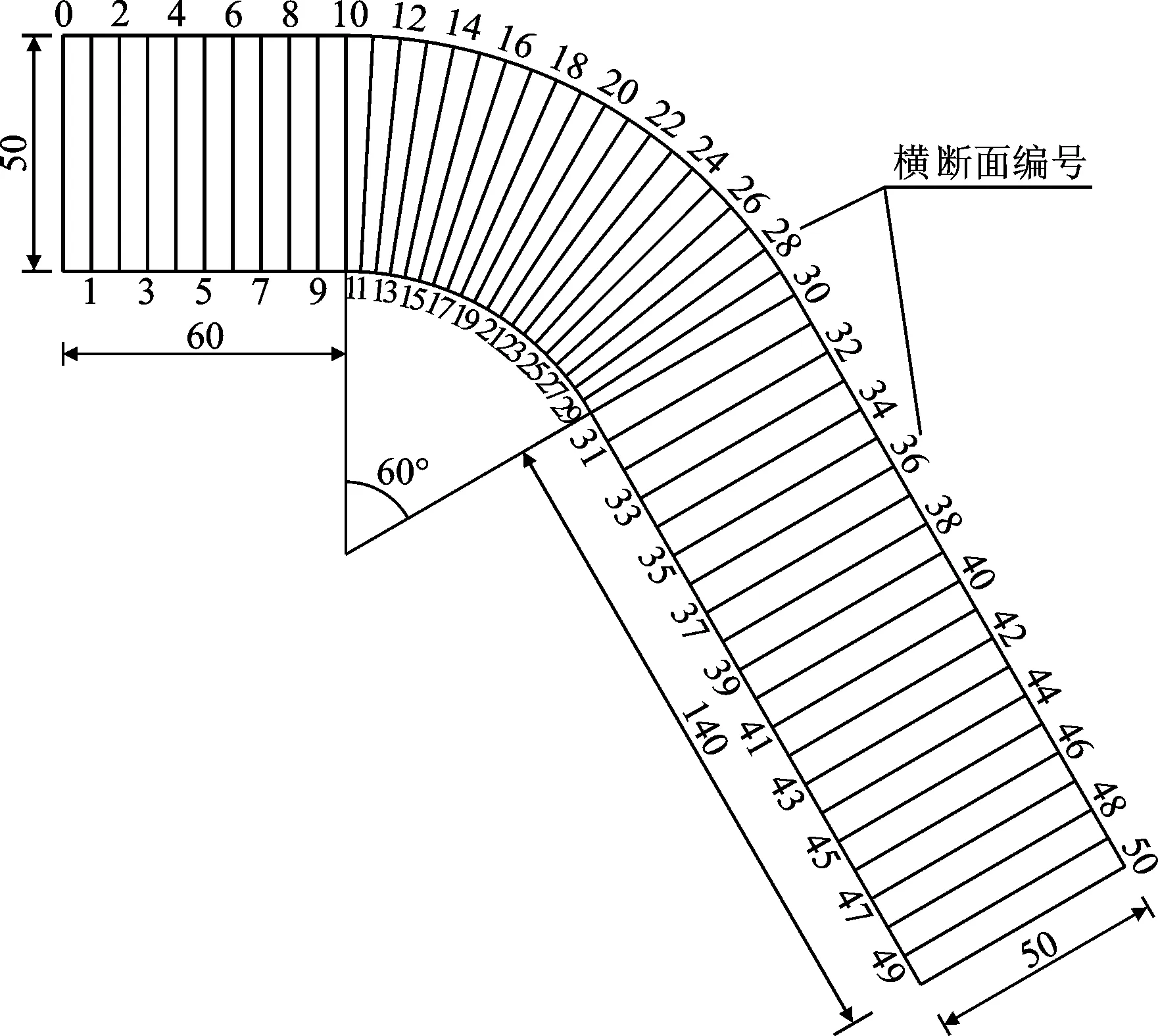
图4 模型量测断面布置图(单位：cm)

试验流量量测采用直角三角形薄壁堰。

试验水深量测采用水位测针，精度为0.1 mm。水位量测共分50个断面，每个断面从左至右每隔5.0 cm布置一个测点，共11个测点；试验流速量测采用毕托管，量测过程中将毕托管置于在1/3水深处，测得时均流速。流速量测共分17个断面，断面编号分别为0#、3#、6#、9#、12#、15#、18#、21#、24#、27#、30#、33#、36#、39#、42#、45#、48#，每个断面从左至右均匀选取6个测点。具体的水深及流速量测测点布置如图5所示。

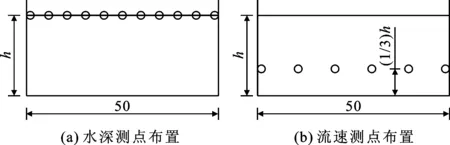
图5 水深及流速量测横断面测点图(单位：cm)

3 试验结果与分析

3.1 弯道水流各评价指标的测试结果与分析

3.1.1 加糙水位变化率 水流进入弯道时，由于离心力较大，使得弯道段凹岸水位明显高于凸岸。试验设置不同工况的糙条，以改变凹凸岸水位差，使其趋于同一水位。无糙条工况与有糙条工况下模型弯道段水流流态对比如图6所示。

图6 无糙条工况与有糙条工况下弯道段水流流态对比

为量化比较加糙与无糙条工况的水位变化，引入加糙水位变化率，定义为：

(1)

α0=0

(2)

式中：αZ为断面水位变化率；Z0为i测点处无糙条工况的水位，cm；Zi为i测点处加糙条工况的水位，cm；α0为无糙条工况下的加糙水位变化率。αZ越大，说明糙条消减动能效果越明显，使得水流紊动强度减小，水面结构调稳幅度较大，动能分配较均匀。

根据弯道段壅水程度，选择横断面15#和横断面20#作为弯道段典型断面，不同工况下典型断面加糙水位变化率如图7所示。由图7可看出，设置糙条可明显增大加糙水位变化率，15#横断面加糙水位变化率基本呈横“S”型变化，且在5#和6#测点处的平均加糙水位变化率较大，而5#和6#测点恰好处于流道中心轴线处；20#横断面为弯顶断面，加糙水位变化率基本呈下降趋势，凸岸加糙水位变化率大于凹岸，这恰好使得无糙条工况相差较大的凸凹岸水深趋于相同，可有效解决弯道凸岸水深小于凹岸水深的不利流态。

图7 不同工况下弯道段典型断面的加糙水位变化率

3.1.2 水面线 水面线可作为描述不同工况下水面变化的重要指标。本文简化水面线的传统做法，可更直观表现出不同工况下沿程水深变化。图8为不同工况下水面线沿程变化规律。由图8可知，对于加设糙条的工况，0#～10#横断面(进口直段)水深均变大，这是由于糙条使得流入弯道的水流壅高，对进入弯道前的水流也产生了影响，这也是试验设计进口直段的意义所在；11#～30#断面(弯段)水深变化较为均匀，可见糙条对水面结构有重分布的作用，使得水流横断面分布较为均匀(可参考图7)；31#～50#断面(出口直段)水深变化较小，但均呈现出水深减小的情况，这说明弯道糙条对水流有消减作用，使得一部分能量在弯段耗散，导致下游出口水流水深减小；随着糙条高度的增大，水面线越趋于平稳，水流流态改善效果越好。

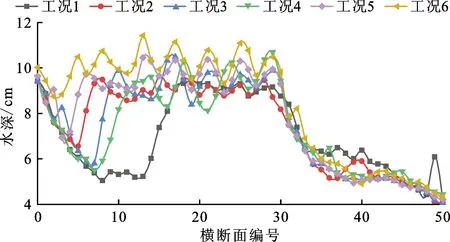
图8 不同工况下溢洪道模型水面线沿程变化规律

3.1.3 横断面均匀度 横断面均匀度可作为衡量水面结构的指标。选取典型断面15#、18#、21#、42#分析横断面水深变化，更直观表现出加设糙条后横断面均匀度的变化，图9为6种不同工况下各典型横断面水深变化。由图9可见，加设糙条后的工况相比无糙条工况(工况1)而言，横断面的水深均有良好改善，趋于均匀化，凹凸岸水位差明显减小，且水位在弯道轴线附近的变化较大，尤其在6#测点处，说明加设糙条对弯道水流流态有很大的影响，使其流态重分布。从图9也可看出，相对于其他工况，工况6横断面均匀度较好，水深变化平稳，改善效果较好，说明糙条高度2.4～1.2 cm与条距18 cm的组合参数较优。

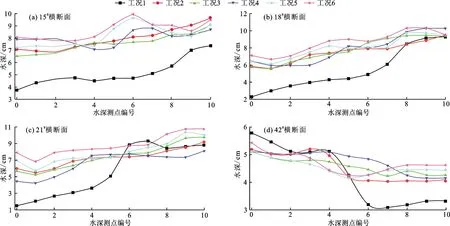
图9 不同工况下典型横断面均匀度变化规律

3.1.4 水面横比降 水面横向比降的计算公式[10]如下：

(3)

式中：Z凹为凹岸水深，cm；Z凸为凸岸水深，cm；B为弯段溢洪道宽度，取50 cm。

图10为6种工况下水面横向比降沿程变化情况。从图10可知，相比无糙条工况1，设置糙条可明显减小水面横比降的变化幅度，从而降低凹凸岸的水位差。糙条高度一定的情况下，随着条距的增大，水面横比降变化幅度增大；条距一定的情况下，随着糙条高度的增大，水面横比降变化幅度减小。说明糙条条距的减小和糙条高度的增大均可使水面横比降减小。

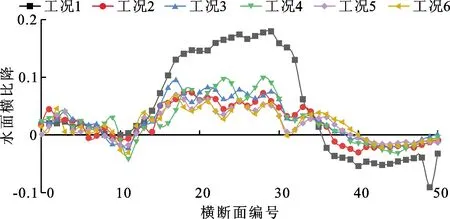
图10 各工况下水面横比降沿程变化

3.1.5 断面流速分布 断面流速分布是弯道水流分析评价的重要指标。为说明试验沿程横断面流速分布情况，分别在进口直段、弯道段、出口调整段选取典型断面，各典型断面编号为6#、15#、21#、42#。各典型断面在不同工况下的流速分布如图11所示。由图11可知，相比无糙条工况1，弯道段在布置糙条后流速明显大幅度减小，6#、15#、21#断面为弯道水流出弯前的断面，可见布置糙条可使流速进行重分布，断面流速分布尽量均匀，这也可较快使动能在横断面上重分配，缩短下游水流调整长度，使冲击波范围减小。42#断面为下游出口调整段的断面，布置糙条可使其流速明显降低。

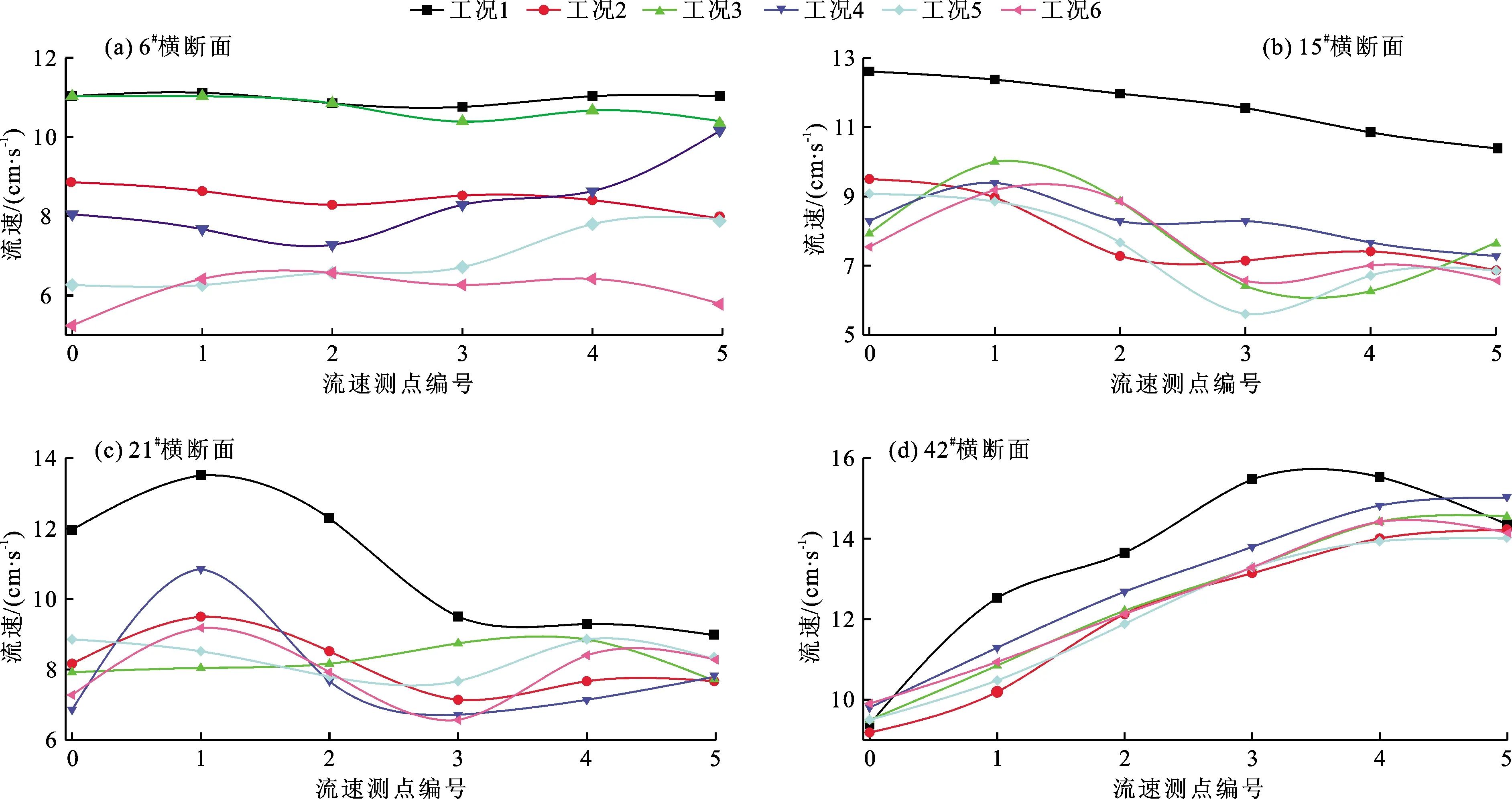
图11 不同工况下各典型断面的流速分布

3.1.6 下游水流恢复长度 水流流出弯道后，边墙偏转变化较大，并受到水流边界和离心力的影响，形成折冲波。无糙条工况与有糙条工况下的模型下游水流流态对比如图12所示。由图12可见，无糙条工况下，下游凹岸水深明显高于凸岸，断面流速分布不均，折冲波的波峰和波谷相互交替出现在两岸，水面出现明显超高现象，导致水流流态恶化，下游水流恢复长度较长。有糙条工况下，由于弯道段布置糙条后，先对弯道段水流进行流态调整，当水流流出弯道段后，由于在弯道段已经调整了水流流态，使得下游水流调整段的长度缩短，能够快速达到了平稳状态。试验中观察到，随着糙条高度的增大，下游水流恢复长度逐渐减小，能更快地使得下游横断面水深趋于均匀化。

图12 无糙条工况与有糙条工况下的模型下游水流流态对比

3.2 糙条对弯道水流动能调整作用

3.2.1 动能计算 水流流入弯道后，凹凸岸水深相差较大，断面流速分布不均，水流流态紊乱，这些均为影响断面动能分布均匀度的重要因素。试验设置糙条后，水流与糙条的撞击过程消耗了水流的部分动能，考虑到弯道段凹凸岸水深不同，凹岸水深远大于凸岸水深，糙条体型选择为梯形断面，这种糙条能改善弯道水流原流态并使其进行动能重新分布。单位重量水体具有的动能公式为：

(4)

式中：αi为动能修正系数，其值取决于过水断面的流速分布，对于渐变流，工程中常取αi=1.0；vi为断面平均流速，cm/s。g为重力加速度，取9.81 m/s2。为比较无糙条工况和有糙条工况的动能分布差异，利用公式(4)计算出不同工况下弯道段典型横断面动能分布，结果如表2所示。

由表2可知，布置糙条的工况2～6与无糙条工况1相比，弯道段动能总和均有所减小，最大动能消减率可达到50%以上。试验表明，布置糙条后，弯道段的水流流态被打乱，各断面流速及动能进行重分布，且弯道段的动能重分配直接影响到了下游出口调整段的流态，使流态恢复平稳，下游水流恢复长度缩短。

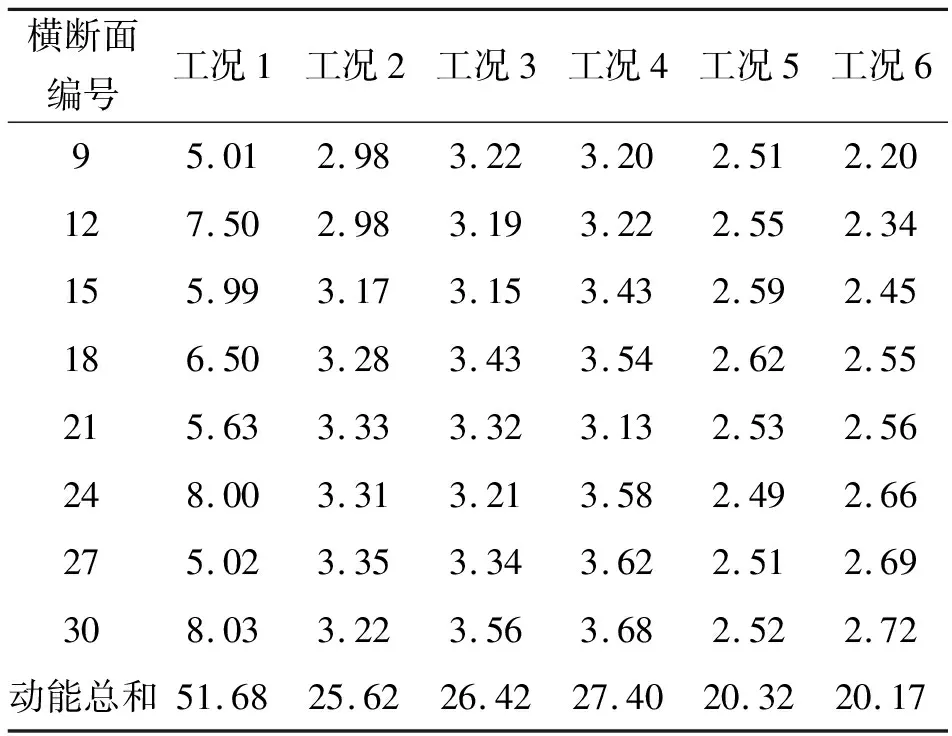
表2 不同工况弯道段典型横断面动能分布计算结果 cm

3.2.2 动能调整系数 为量化糙条对断面动能调整的程度，引入动能调整系数：

(5)

式中：σ为动能调整系数；Ei为第i个断面的动能，cm；∑Ei为弯道段的动能总和，cm。

利用公式(5)计算不同工况下弯道段典型断面的动能调整系数，计算结果如表3所示。

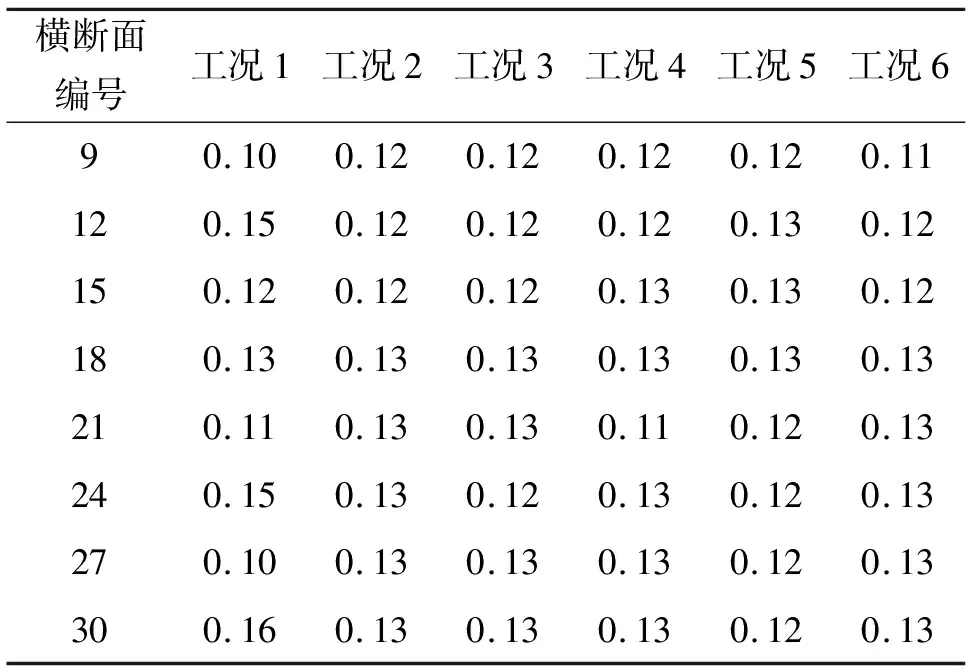
表3 不同工况弯道段典型横断面动能调整系数σ计算结果

由表3可知，工况1(无糙条)弯道段凸岸和凹岸的动能调整系数相差6%，各典型断面动能分布不均匀，也反映出无糙条布置的工况下凹凸岸水位差相差较大，流态不稳定，流速分布不均匀。布置糙条的工况2～6，弯道段各典型断面动能调整系数有明显的变化，使得动能分布较为均匀，每种工况的各典型断面的动能调整系数均逐渐趋近于同一个值，反映出布置糙条后流态得到显著改善。

4 结 论

本文针对糙条消能工对弯道水流动能调整进行了模型试验和分析研究，得出以下结论：

(1)通过6种工况的模型试验和研究发现，不同布置型式的糙条消能工均可有效对弯道水流进行动能调整，使得动能进行重分配，可明显削减弯道段水流的动能，降低流速，缩短下游水流恢复长度。

(2)通过对有糙条工况下加糙水位变化率的计算和分析，得到布置糙条可明显加大加糙水位变化率。弯顶段断面凸岸的加糙水位变化率大于凹岸的加糙水位变化率，有效降低了弯顶段严重的水面超高现象和凹凸岸的水位差。弯顶之前的弯道段加糙水位变化率基本呈横“S”型趋势变化，在流道中心轴线处加糙水位变化率较大。

(3)通过对水面线、横断面均匀度、水面横比降等评价指标的分析，糙条凹凸岸高度不同且在糙条高度增大和条距减小时，水深沿程变化较为规律，横断面均匀度趋于平稳，水面横比降变化幅度明显减小，但糙条凹凸岸最高高度小于2.0 cm且条距较大时，将出现负面影响，水流流态改善效果不佳。

(4)通过计算弯道各典型断面动能调整系数发现，糙条的布置可使弯道段的最高动能消减率达到50%以上，不同工况下各典型断面动能调整系数得到均匀分布，逐渐趋近于同一个值，动能调整效果明显。因此，相比其他消能工，糙条消能工布置型式简单，其作用及效果十分显著，施工简便，可为实际工程设计等提供参考依据。