基于短期数据推算宣城市的设计风速
向佳颖,庄峻淇,项何婷,陈奕名 (合肥工业大学宣城校区,安徽 宣城 242000)
1 引言
我国幅员辽阔,地形、地貌复杂多变,尤其是近海地区、平原和山区,风速、风向的变化差异较大。即使建立了许多气象风速、风向观测站,但对于局部复杂的地形环境还不能较准确地反映该地的风速、风向特征,有些地方观测资料少,缺乏多年连续观测资料。在工程应用中,确定设计风速是一个基本问题,资料短缺会给设计的准确性与建筑工程的安全性带来影响。因此,合理正确利用短期数据来推算设计风速是一个重要的研究方向[1][2]。
目前建设的风电场大多位于偏远地区,缺少长期测风资料,丘海珊、曹秋会、孔静[3]利用短期实测资料推算出该处50年一遇10m高10min平均最大风速,并对比常规风速推求方法,证实了短期资料系列推算方法的合理性。胡金宝[4]等依据气象站与测风塔的位置建立关系,用最小一乘法将不同频率设计风速移用到测风塔处;在风速观测数据不足时,于舰涵、李明水、李少鹏、廖海黎[5]等采用极值Ⅰ型分布获得了风速的月极值分布和年极值分布的关系,并应用风速风向联合分布函数推算出设计风速。刘聪[6]等采用极值频率分布拟合方法,分析计算得到大桥建设所需的设计基本风速和基准风速。风速过程作为平稳高斯随机过程,风速母体服从指数型分布。所以,可以基于时段最大取样和跨阈取样法,研究极值风速理论分布的特征,利用极值Ⅰ型分布、威布尔分布和广义Pareto分布等分析概型的尾部特性,研究对于极值风速的估计精度[7]。推算设计风速时,可以使用基于实测风速数据的区组模型和超阈值模型,以及基于选址处观测站和附近气象站同期数据相关性的方法和虚拟气象站法[8]。
基于短期实测风速数据,本文采用区组模型和超阈值模型分析风速分布情况,推算出了选址处的设计风速,并将两种模型在重现期为10年、30年、50年、100年下的风速作出了比较。
2 实测风速分析
小组利用了学校观测站在2016年8月至11月以及2017年4月至7月共计8个月的风速数据。宣城市季风气候现象比较明显,图1、图2为观测期内日最大平均风速分布图。
从图1中的实测数据可以看出:观测期内较大风速主要出现在4月、7月、8月和9月,其它月份出现大风的概率较小。各月的最大平均风速情况如表1。据统计,观测期内日最大瞬时风速的均值为7.32m/s,标准差为2.07m/s,观测期内所有日最大瞬时风速的最大值为16.35m/s,出现在2017年7月13日。观测期内日最大平均风速的均值为2.26m/s,标准差为0.66m/s,观测期内所有日最大平均风速的最大值,出现在2017年7月13日。可以发现宣城市7月份的风资源较为丰富,利用空间很大。
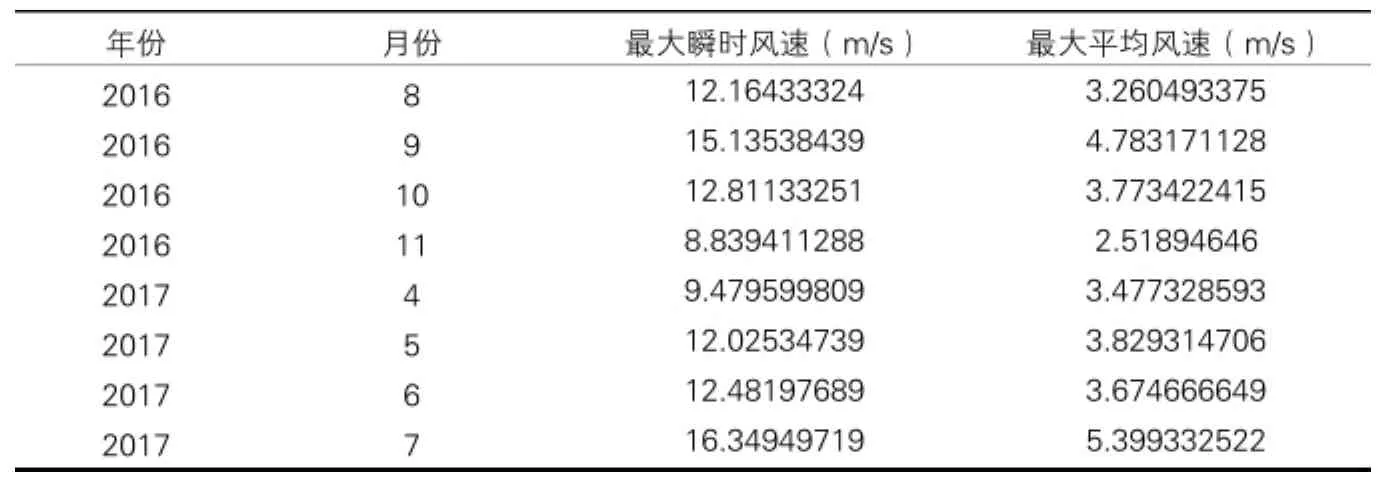
月最大风速 表1
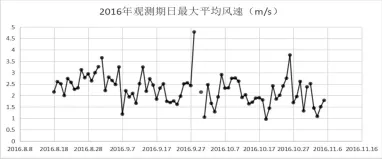
图1 2016年观测期内日最大平均风速图式
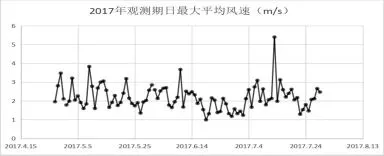
图2 2017年观测期内日最大平均风速图式
3 设计风速的计算
3.1 区组模型
经典极值理论认为,不论随机变量服从何种形式的分布,它的极值分布都可以统一于广义极值(GEV)分布,其形式如下:

其中μ、σ和ξ分别为位置参数、尺度参数和形状参数。
当利用区组模型拟合风速的年最大分布时,一般是将每年的风速数据作为一个区组,以年最大风速值作为样本。但是由于我们仅有观测期内8个月的风速数据,没有丰富的年最大风速的样本。Grigoriu认为,对于短期数据,可采用月最大风速来推算年最大风速分布[9]。这里假定各月的月最大风速满足独立同分布的条件,将每个月的风速数据作为一个区组,以月最大风速值为样本进行拟合。
此时,风速的年最大分布和月最大分布满足:Fa(x)=[Fm(x)]12其中Fa和Fm分别为风速年最大和月最大分布[2]。基于GEV分布,我们有

式中:μm、σm和ξm分别表示Fm的位置、尺度和形状参数。
我们将上表表1的数据作为样本,根据得到的样本,利用MATLAB算得GEV的位置参数、形状参数和尺度参数:μm=3.4979,σm=0.7462,ξm=-0.1443。
同时我们也可以将(2)式转化为标准的GEV分布,其中满足:
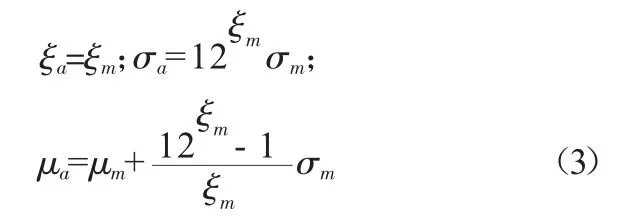
其中μa、σa和ξa分别表示Fa的位置、尺度和形状参数。
当ξ趋于0时,式(3)可转化成Gumbel分布,此时年最大分布和月最大分布的参数关系为:
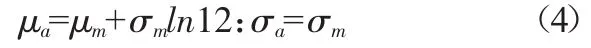
根据上述式子计算出相应参数,可求出不同重现期下的设计风速,见表2。
3.2 超阈值模型
区组模型方法只提取每个区组中的最大值作为样本点,这样的选取造成了数据的严重损失,且无法有效利用更多的极值信息。尤其是在只使用短期数据的情况下,这些问题将更加显著。为了充分利用数据中的极值信息,可以选定一个阈值,将超过该阈值的所有数据集中建立超阈值模型。广义Pareto分布(GPD)是描述超阈值分布函数的合理模型[10],如下:

式中:是选取的阈值;ξ*是形状参数;σ*是尺度参数。
若ξ*=0,此时得到的极值分布可转变成Gumbel分布,上述的(5)式可转变为:

在此之前,要对阈值进行选取,参考均值加上1.4倍数据的标准差可以得到经验阈值。最终选取的阈值为x0=1.9247m/s,并从中挑出112个超过当年阈值风速的风速数据。
根据2016年和2017年观测期内的所有超阈值风速数据,可以观察得出,大风天气可能会连续出现。通过对所有超阈值样本的分析发现,超过阈值风速的的时间基本能维持2~4天,有时甚至能维持一周。因此,在计算设计风速时应避免如此类相关性较大的风速数据,所以必须从其中挑选独立的数据。Simiu和Heckert[11]的做法是将日最大风速数据分为4 d或者8 d作为一个周期,选取每个周期的最大值,且相邻的最大值的间距不能小于半个周期,进而从超阈值数据中获得37个超阈值样本。
根据得到的样本,利用MATLAB中的相应函数,计算出相应的GPD参数:形状参数ξ*=-0.6784以及尺度参数σ*=3.6912。
再根据上述(5)、(6)两个式子分别计算出设计风速,如表3。

不同重现期下的设计风速(区组模型) 表2

不同重现期下的设计风速(超阈值模型) 表3
4 结论
①从GEV分布和Gumbel分布算得的设计风速可以看出,GEV分布推算得到的设计风速总体偏小且不同重现期下风速差异小,所以采用Gumbel分布更为合理。利用广义Pareto分布(GPD)计算设计风速时,当形状系数不为0时得到的数值较小,且在不同重现期下风速差异也较小,所以对于短期数据,建议采用形状系数为0的情况。
②基于区组模型和超阈值模型算出宣城地区的设计风速分别为7.7357m/s和22.2816m/s。本文只是利用现有气象观测站短期资料进行的设计风速初步估算,由于风速分布并不均匀,所以两种模型得出的设计风速不同。
③宣城地区风速修正系数有一定差异,还应根据具体情况做进一步修正。

