基于相关向量机的发动机剩余寿命预测

彭鸿博, 蒋雄伟

(中国民航大学航空工程学院，天津300300)

民航发动机的维修与保障对于飞机的安全运行至关重要，基于发动机剩余寿命(remaining useful life, RUL)预测来确定下发期限能够为发动机工程师制定科学合理的维修方案提供依据。由于民航发动机使用可靠性高、运行周期长，因此利用传统的统计方法收集失效数据建立统计模型进行寿命预测比较困难[1-2]。并且航空发动机是囊括了机、电、液的复杂系统，失效模式较多，基于失效机理建立物理模型准确预测剩余寿命的方法只能针对发动机的某个部件，不适用于整机[3-4]。

民航发动机在运行过程中必须进行状态监控，监测参数的变化情况能够反映发动机的健康状态，利用性能退化数据挖掘发动机的性能衰退规律，通过统计推断和机器学习等方法预测剩余寿命是目前研究的热点。基于状态监控的剩余寿命预测通常采用的思路是选取单个或多个监测参数作为发动机性能衰退的退化量，通过预测退化量达到失效阈值的时间来实现发动机剩余寿命的预测。马小骏等[5]采用排气温度裕度(exhaust gas temperature margin, EGTM)作为性能衰退的指标，通过分析发动机EGTM的发展趋势，采用最小二乘支持向量机(least squares-support vector machine, LS-SVM)建立性能可靠性模型来预测发动机的在翼寿命；黄亮等[6]根据发动机的历史性能监测数据，在考虑发动机性能退化过程非线性和多阶段特点的基础上，建立Wiener退化模型并采用贝叶斯方法更新模型参数，通过预测排气温度(exhaust gas temperature, EGT)超过失效阈值的时间来预测剩余寿命。

与使用单性能参数的预测方法相比，基于多个性能参数预测发动机剩余寿命的方法能够更有效地利用监测数据，预测的准确性也更高。张颉健[7]根据发动机采集的监测参数为多维离散型数据的特点，通过改进过程神经网络使其能够满足离散输入与多个参数融合的要求，建立了发动机性能状态预测模型；Nieto等[8]采用支持向量机(support vector machine, SVM)挖掘性能参数与发动机剩余寿命之间的对应关系，建立了直接预测模型，并针对SVM需要优化的模型参数较多的问题采用粒子群算法进行了参数寻优；Babu等[9]将深度卷积神经网络引入到复杂设备剩余寿命预测领域中，分析其可行性并使用发动机性能退化仿真数据集进行了验证；Ordóez等[10]利用自回归滑动平均模型(autoregressive integrated moving average model, ARIMA)对发动机各监测参数分别进行预测，再以多维参数的预测值作为SVM的输入，以发动机剩余寿命为输出，建立了预测模型；宋亚等[11]将自编码神经网络(autoencoder)和双向长短期记忆(bidirectional long short-term memory, BLSTM)神经网络进行整合，结合两者的优势提出了一种混合健康状态预测模型，并将其用于涡扇发动机的剩余寿命预测。

前人研究中主要依靠机器学习算法较强的非线性映射能力直接建立发动机性能参数与剩余寿命的关系，然而预测过程中监测参数的选取对预测结果的影响较大，监测参数筛除较多容易导致信息遗漏，保留过多的监测参数又会使模型误差累积过大，预测精度降低。为此，在发动机所有监测参数的基础上，应用核主元分析(kernel principle component analysis, KPCA)算法提取出包含发动机性能衰退信息的低维特征，并进行非线性融合得到描述发动机退化轨迹的健康指数(health index,H)序列，再利用相关向量机(relevance vector machine，RVM)建立回归模型，通过外推预测H超过失效阈值的时间，间接获取发动机剩余寿命的预测值。

1 退化特征信息融合

民航发动机在不考虑维修的情况下，其性能衰退过程可近似地视为不可逆的单调退化过程，退化趋势通过监测的性能参数变化情况表现，但不同参数对发动机退化程度的敏感程度不同，并且各参数之间存在一定的相关性，因此需要对原始监测数据进行处理，将其融合成能够反映发动机退化趋势的健康指数。

1.1 基于KPCA的退化特征提取

核主元分析是一种将核函数与主元分析(principle component analysis, PCA)结合的数据处理方法，主要针对信息融合中的非线性问题，其基本原理是通过非线性映射将原始数据投影到高维特征空间，然后在高维空间中执行主元分析，消除原始数据中的冗余信息，提取出能够描述原始数据变化趋势的主元序列[12]。民航发动机运行过程中监测的性能参数较多，且各参数之间存在一定的非线性关系，为此采用KPCA对监测数据进行处理。

假设采集到的发动机性能监测数据为X=[x1,x2,…，xN]∈RM×N，其中N为性能参数的个数，xi=[x1,x2,…,xM]T表示第i个监测参数的时间序列，对其进行核主元分析的步骤如下。

(1)首先对监测数据进行标准化预处理，处理后得到矩阵X*，其均值为0，方差为1。

(2)选择核函数，并求核函数矩阵K。根据监测数据的特点，采用的核函数为高斯径向基核函数：

K(xi,xj)=exp(-‖xi-xj‖2/σ)

(1)

式(1)中：σ为核函数宽度。采用交叉验证的方法选取最佳的核函数宽度值。

K′=K-INK-KIN+INKIN

(2)

式(2)中：IN为N维单位矩阵。

(4)求协方差矩阵的特征向量ν和特征值λi，将主对角线上为特征值的对角阵变换成特征值列向量，特征值按降序排列：λ1≥λ2≥…≥λN。

(5)以主元贡献率为依据提取前p(p≤N)个主元，对应的特征向量可组成特征向量矩阵V=[ν1,ν2,…,νp]。为保证最大程度保留原有信息量的同时又实现特征空间的降维，设定累计主元贡献率rCS必须大于85%，计算公式为

(3)

式(3)中：λi为前p个主元的特征值；λj为全部特征值。

(6)计算原始数据在特征向量矩阵V上的投影，输入样本x在第k个主元νk上的投影为

2,…,p

(4)

式(4)中：Φ(·)为映射函数；αi为特征向量的系数。

得到发动机性能监测数据的核主元特征为X′=[t1,t2,…,tp]，其中tp=[t1,t2,…,tM]T表示第p个主元的时间序列。

1.2 健康指数的计算方法

经过核主元分析处理后得到的主元序列，既保留了原始数据的特征信息，又在维度上实现了约简，但其不能够直接反映发动机性能衰退的趋势，因此在发动机性能监测数据核主元特征的基础上，将主元序列融合成健康指数来表征系统的健康程度，其衰减的过程对应发动机性能退化的过程[13]。根据发动机性能衰退的特点，采用非线性模型：

y=aeX′BT+c

(5)

式(5)中：a、B=[b1,b2,…,bp]为非线性融合模型的系数；c为常数项；y为发动机的健康指数序列。

该模型可建立核主元特征X′与健康指数y之间的关系，利用该模型来融合多维主元序列可得到一维的发动机健康指数(health index,H)序列。为了求解模型系数，需要构造训练样本集，令发动机刚开始使用时前5个飞行循环H=1，因性能衰退需要下发时后5个飞行循环H=0，得到训练样本集：

(6)

式(6)中:X′M为原始数据第M个样本在特征空间上的投影，使用训练样本集Ω来训练模型，可获得模型系数a、b1，b2，…，bp和常数项c的值。通过非线性模型融合得到的发动机H序列，不仅保留了发动机性能衰退的信息，而且能够直接反映发动机的性能衰退过程。

2 基于RVM的发动机RUL预测

基于RVM的发动机剩余寿命预测主要包括训练过程和测试过程两个阶段。训练阶段从发动机历史失效数据中获取完整H序列作为输入，建立RVM模型；测试阶段利用训练获得的RVM模型对发动机当前的H序列进行外推预测，获取H预测值，比较H超过失效阈值的时间和预测起始时刻，计算发动机的剩余寿命，预测方法的框架如图1所示。

图1 RUL预测框架Fig.1 RUL prediction frame diagram

2.1 RVM模型

相关向量机是一种将Bayesian理论与SVM结合的机器学习算法。相比SVM，RVM的核函数没有特殊限制，稀疏性更好，较少的超参数降低了核函数的计算量，且具有概率形式的输出，可用于时间序列的分析与预测[14]。因此，将RVM用于民航发动机RUL预测。

(7)

式(7)中：n为样本数；ω=(ω0,ω1,…,ωn)T为模型参数；K(x,xi)为非线性核函数。

RVM模型的预测过程如下。

(1)设定超参数α和噪声方差σ2的初始值。α为由N+1个超参数αi组成的向量，α=[α0,α1,…,αN]T，其中αi为权值ω对应的超参数。

(2)采用高斯核函数，根据当前的α和σ2计算模型参数ω的后验分布：

p(ω|y,α,σ2)=N(μ,Σ)

(8)

式(8)中：y=(y1,y2,…,yn)T；α=(α1,α2,…,αn)；N(·)为多变量高斯分布；μ=σ-2ΣΦTy为均值；Σ=(σ-2ΦTΦ+A)-1为协方差，其中A=diag(α1,α2,…,αn)，Φ为n(n+1)维的设计矩阵，Φ=[φ(x1),φ(xn),…,φ(xn)]T，其中φ(xi)=[1,K(xi,x1),…,K(xi,xn)]T；均值μ作为发动机H的预测值；协方差Σ表示模型预测的不确定性。

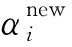
(9)

(10)

式中：γi=1-αiΣii，Σii为协方差矩阵中第i项对角元素；μi为第i个后验期望值。

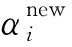
μtest=μTφ(xtest)

(11)

(12)

(5)根据预测均值和方差可以计算预测值的概率密度p(ytest)和分布函数F(ytest)，得到预测值的置信区间。

(6)设定失效阈值作为预测终止条件，截取待测样本预测起始时到H序列超过失效阈值时的飞行循环数作为发动机的剩余寿命预测值。

2.2 模型评价指标

任何方法应用到实际工程中都需要具备一定的实用价值，使用本文方法对待测发动机进行剩余寿命预测后，可用一个或多个评价指标来显示该方法的预测效果。通常采用的评价方法是对多个设备进行寿命预测，选择平均百分比误差(mean absolute percentage error, MAPE)作为评价预测准确性的指标，其计算公式为

(13)

式(13)中：K为待测样本数量，Rpre,d、Ract,d分别表示第d个待测样本剩余寿命的预测值和真实值，Rpre,d-Ract,d表示预测误差，通常MAPE越低代表模型的预测准确度越高。

采用文献[15]中定义的准确预测数量，对于多个样本的预测结果，预测值在真实值周围±α区域[Ract-αLTTF,Ract+αLTTF]内时可视为准确预测，其中Ract为发动机真实剩余寿命值，LTTF为发动机整个寿命长度，α可根据情况设定，取α=0.05。

3 方法验证

采用NASA Ames研究中心提供的发动机退化仿真数据集来验证本文方法，该数据集是基于CMAPSS仿真软件通过一系列航空涡扇发动机从初始状态运行至失效的仿真实验获得。该数据集分为4组，每组数据由独立的仿真实验生成，包括训练数据集、测试数据集和RUL真实值三个部分，同组数据集中的发动机可视为完全相似的发动机，其中训练数据和测试数据的格式为26维时间序列，分别记录了发动机编号、工作循环数、3个发动机工作环境参数(飞行高度、马赫数和油门杆角度)和21个传感器测量值，如表1所示。

表1 传感器数据集描述Table 1 Description of sensor data sets

每台发动机记录数据结束时的Cycle值代表该发动机的寿命。采用数据集1来开展实例研究和方法验证，以其中的#7号发动机为例，训练数据和测试数据分别如表2、表3所示。

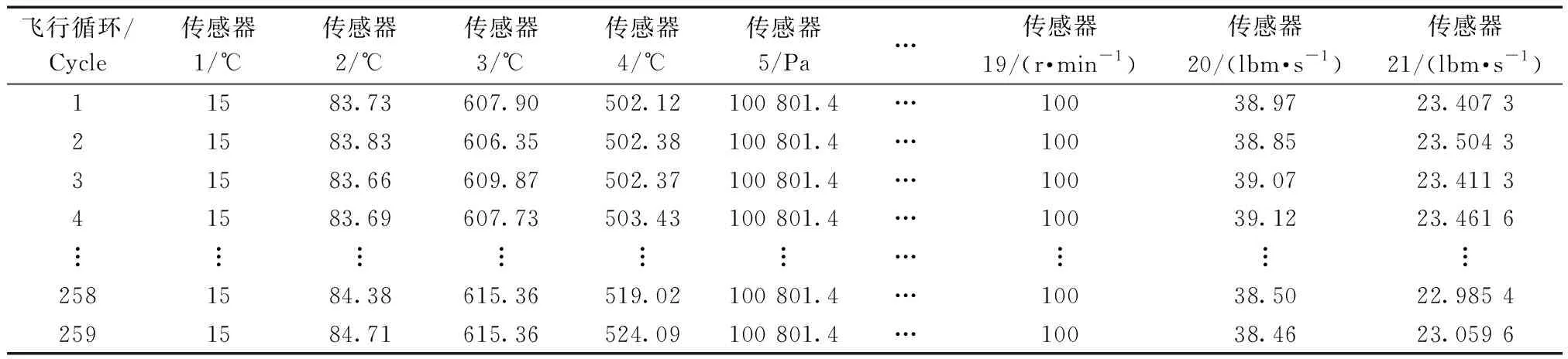
表2 #7号发动机训练数据Table 2 Training data from seventh engine

观察21个传感器测量值序列，发现某些参数为常值，如参数1、5、6、10、16、18、19，在数据集中将这几个序列删除，把剩下的序列作为初始数据进行核主元分析，根据交叉验证的方法确定最佳核函数宽度为3.0，设定最大迭代次数为 1 000，当累计贡献率达到86.7%时得到前3个主元，其时间序列如图2 所示。

图2 #7号发动机的核主元特征Fig.2 KPCA trajectories of seventh engine

选取最初5个飞行循环(令H=1)，以及最后5个飞行循环(令H=0)，将构造的矩阵作为非线性融合模型的训练样本，经计算后可得到模型的系数为[a,b1,b2,b3]=[-196.9,0.023 65,-0.011 02,-0.030 3]，常数项c为197.7。

使用上述的非线性模型对训练数据的3个主元序列进行变换，得到#7号发动机完整的健康指数序列，如图3所示。

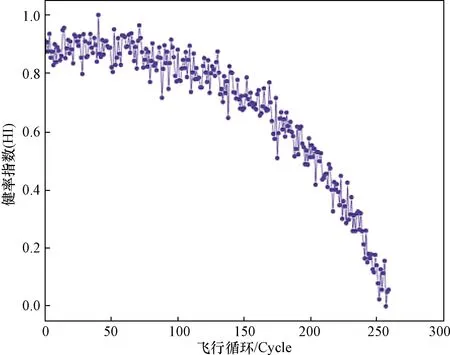
图3 #7号发动机健康指数序列Fig.3 H series of seventh engine

将由训练数据集得到的发动机完整H序列作为RVM模型的训练样本，经训练后可得到模型参数。再将由测试数据集得到的H序列作为测试样本，使用训练后得到的RVM模型对测试样本进行外推预测，设定失效阈值为H=0，超过失效阈值时预测结束，截取预测过程的飞行循环数作为RUL预测值，得到的预测结果和RUL的概率分布分别如图4、图5所示。

图5 #7号发动机RUL概率分布Fig.5 Probability distribution of seventh engine’s RUL

图4 #7号发动机RUL预测结果Fig.4 RUL prediction result of seventh engine

#7号发动机的剩余寿命预测期望ERUL=92，接近其真实寿命(91)。使用本文方法对数据集1中的100个发动机分别进行剩余寿命预测，将预测结果与真实值进行对比，如图6所示。

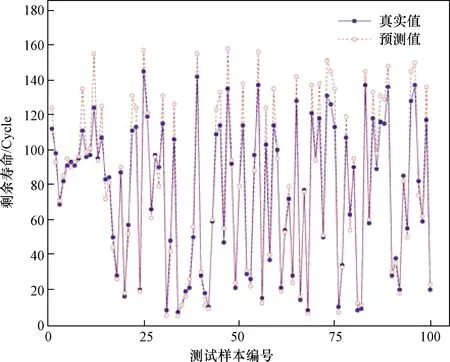
图6 数据集1所有发动机RUL预测结果Fig.6 RUL prediction results of all engines from flight data1

经过对比发现，预测起始时如果发动机H较低，得到的剩余寿命预测值更接近于真实值，预测准确度更高，分析其原因，可能是由于发动机H较高时，现有的H序列反映的发动机退化趋势不明显，导致预测的失效时间存在一定程度的滞后，这与发动机投入使用早期难以预测寿命的实际情况符合。

根据预测结果，按照相关指标与SVM模型和过程神经网络模型的预测结果进行对比。在SVM模型中，选用高斯核函数，通过网格搜索方法优化模型参数，惩罚因子C、核函数参数γ、不敏感损失函数参数ε分别设置为12、0.002、1； 在过程神经网络模型中，神经网络层数设置为3，神经元激励函数选择Sigmoid函数，各层神经元个数为{10、14、1}。通过相关性分析，选择2、3、4、7、11、12、14号传感器数据作为特征参数进行剩余寿命预测。三种方法的预测结果对比如表4所示。

表4 三种预测方法结果对比Table 4 Comparison of the results of three prediction methods

由表4可知，本文方法在各项指标上都明显优于SVM模型和过程神经网络模型。传统的机器学习方法直接使用原始数据来预测发动机剩余寿命，实现多维输入到一维输出的直接映射，由于发动机监测数据维数较多，并且各性能参数之间存在一定的相关性，因此预测误差相对较大。而本文方法利用KPCA对原始数据进行特征提取，有效地消除了冗余信息和参数相关性的干扰，并且特征信息的融合使得RVM模型对发动机剩余寿命的预测更易于实现、预测精度更高。

4 结论

提出了一种基于信息融合与RVM的民航发动机剩余寿命预测方法。该方法是一种间接的RUL预测方法，以发动机失效数据为支撑，能够融合多维退化特征属性为一维健康指数，根据健康指数的发展来预测剩余寿命，预测的准确度较高，符合实际应用要求。相比于通过非线性映射能力比较强的机器学习算法(如SVM和神经网络等)建立监测数据到剩余寿命的关系来实现直接预测的方法，本文方法的预测性能更好，说明其更适用于性能退化情况较为复杂的民航发动机。不过当发动机退化轨迹处于较早时期时，该方法的预测精度会有一定程度的降低，未来需要进一步研究提高预测精度的方法。