高次模碳纤维微波加热装置的设计与实验

张俊杰, 单家芳, 朱 梁, 刘成周, 陈龙威, 马文东

(1.中国科学院等离子体物理研究所，合肥 230031； 2.中国科学技术大学研究生院科学岛分院，合肥 230026)

碳纤维石墨化所需温度一般为2 500～3 000 ℃，经过微波石墨化处理后，其拉伸强度和拉伸模量可以提高10%左右。目前，中国T300碳纤维材料主要应用于体育休闲产品，而应用于航空航天、汽车等领域的高强度、高模量石墨化碳纤维尚处于研发中，且需求量巨大[1]。常用的碳纤维石墨化加热装置主要包括电阻炉和高频感应炉。电阻炉需要先将炉膛加热至石墨化反应温度，再以热辐射的形式将热量传递至碳纤维表面，缺点为加热效率低、加热不均匀以及炉膛寿命较短；高频感应炉是在加热区域产生高频交变磁场，碳纤维在交变磁场感应下产生电涡流进行加热，这种加热方式升温速度快，缺点为碳纤维自身的电导率各不相同，导致加热不均匀[2-3]。微波加热是材料在电磁场中由于自身的介质损耗而引起的整体加热。微波加热具有加热速度快、加热均匀及选择性加热等优势[4-5]，可用于加热碳纤维。在腔体表面积相同的情况下，圆柱腔的品质因数(Q)高于矩形腔，Q越高，储能特性越好故微波加热一般采用圆柱形谐振腔[6]。Metaxas[7]将介质加载到工作频率为896 MHz的TM010横磁波模式圆柱腔轴向电场Ez最大的位置，通过实验研究了各种液体食品的加热效率；Bhartia等[8]通过实验验证了工作于TM115模的圆柱腔处理表面材料和加热液体的可行性，圆柱腔的可用功率主要集中在被处理材料所占据的区域。

目前，中外少有公开发表的有关碳纤维微波加热技术的研究文献，为了实现碳纤维的微波石墨化，有必要对碳纤维微波加热装置进行研究。为此，设计一种基于TM110模的圆柱谐振腔，建立多物理场耦合的三维仿真模型，利用该模型研究了圆柱腔的谐振特性和微波加热效果，并通过实验验证碳纤维微波加热的可行性和装置的有效性。以期为后续的碳纤维微波石墨化研究提供理论和实验指导。

1 圆柱谐振腔的设计

1.1 理论分析

圆柱腔TEnml横电波模式的谐振频率f0与腔体尺寸的关系为

(1)

圆柱腔TMnml横磁波模式的谐振频率f0与腔体尺寸的关系为

(2)

由式(2)得出TM110模的谐振频率f0与腔体直径的关系为

(3)

相较于2.45 GHz的圆柱腔，915 MHz的圆柱腔能够处理直径较大的介质[7]，这有利于在腔体两侧轴向电场最大区域同时加载多束碳纤维进行加热，提高加热效率。当f0=915 MHz时，D=400 mm，根据式(1)、式(2)绘制出无量纲的圆柱腔谐振模式，如图1所示。

图1 圆柱腔的谐振模式图Fig.1 Resonant mode diagram of cylindrical cavity

由图1可知，为尽可能避免TM011和TE111等杂模的产生，应满足(D/h)2>4.58，即h<187 mm。同时，为了保证碳纤维石墨化连续加工的效率，腔体高度应尽可能大。综合考虑上述因素，初步确定D=400 mm，h=180 mm。

1.2 耦合方式的选择

圆柱谐振腔与外电路的耦合方式主要包括电场耦合、磁场耦合以及电磁耦合[6]。完整的可以连续加工的碳纤维微波石墨化装置，除了微波加热腔体以外，还包括用于收放丝的牵伸装置、调速电机、惰性气体密封装置、气冷和水冷装置等[10]，体积庞大、结构复杂，所以应尽可能简化微波加热部分的结构，便于今后工业化应用。传统的圆柱谐振腔是由工作于TE10模的矩形波导，通过耦合孔将微波耦合到腔体中，这种方式体积较大、成本较高，也不便于调谐。采用特性阻抗为50 Ω的同轴线电磁耦合的方式将微波馈入腔体，通过调整旋转刻度板，改变同轴线内导体与腔体的相对位置，使加入碳纤维后的腔体输入阻抗发生变化，实现阻抗匹配和调谐的目的[11]。同轴线由直径D2=10 mm，长度l2=5 mm 的圆柱体聚四氟乙烯和直径D3=3 mm，长度l3=205 mm的内导体铜组成，内导体一端穿入聚四氟乙烯，另一端穿入上侧端盖，保证耦合的稳定性。

2 圆柱谐振腔的仿真与实验

2.1 腔体尺寸的仿真与实验

实验采用中心频率为915 MHz的固态微波源，为了提高微波的利用率，腔体的谐振频率应尽可能接近915 MHz。但通过仿真和实验发现D=400 mm，H=180 mm的TM110单模腔在加入碳纤维后难以同时满足谐振频率和阻抗匹配的要求。结合仿真和实验结果，确定腔体的仿真和加工尺寸为D=410 mm，h=200 mm，耦合点的调节范围d=120～150 mm。图2、图3分别为d=150 mm时空腔的TM110模电场和磁场分布。由图2、图3可以看出该尺寸下TM110模为腔体的主模，TM011和TE111等少量杂模对微波加热的影响可以忽略不计。

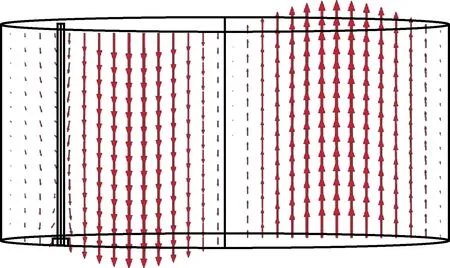
图2 空腔的电场分布Fig.2 Electric field distribution of the empty cavity

图3 空腔的磁场分布Fig.3 Magnetic field distribution of the empty cavity

图4(a)为输入功率1 W时，腔体的xz纵截面不同高度处沿x方向的电场强度分布图，图4(b)为输入功率1 W时，腔体的yz纵截面不同高度处沿y方向的电场强度分布图。由图4可以看出，耦合点与腔体中心连线的xz纵截面电场强度比yz纵截面电场强度高一个数量级，且xz纵截面上腔体两侧电场集中区的直径均大于15 mm。因此取石英玻璃管内径D1=15 mm，在腔体xz纵截面两侧电场最大的位置各打一个直径20 mm的通孔，穿入玻璃管，然后加入碳纤维，两端由内含陶瓷的金属塞固定和密封，通孔圆心到腔体中心的距离分别为x1=81 mm，x2=102 mm。

图4 空腔的纵截面电场分布Fig.4 Electric field distribution of longitudinal section in the empty cavity

图5为两侧各加入4束(12×103根)碳纤维负载后的圆柱腔模型图，碳纤维外部为石英玻璃管，用于通入氮气，防止碳纤维高温氧化，内径D1=15 mm，厚度d1=1 mm，长度l1=390 mm；玻璃管外部为金属铝屏蔽套筒，用于固定碳纤维和玻璃管，防止微波泄漏。表1为圆柱谐振腔的主要尺寸参数。

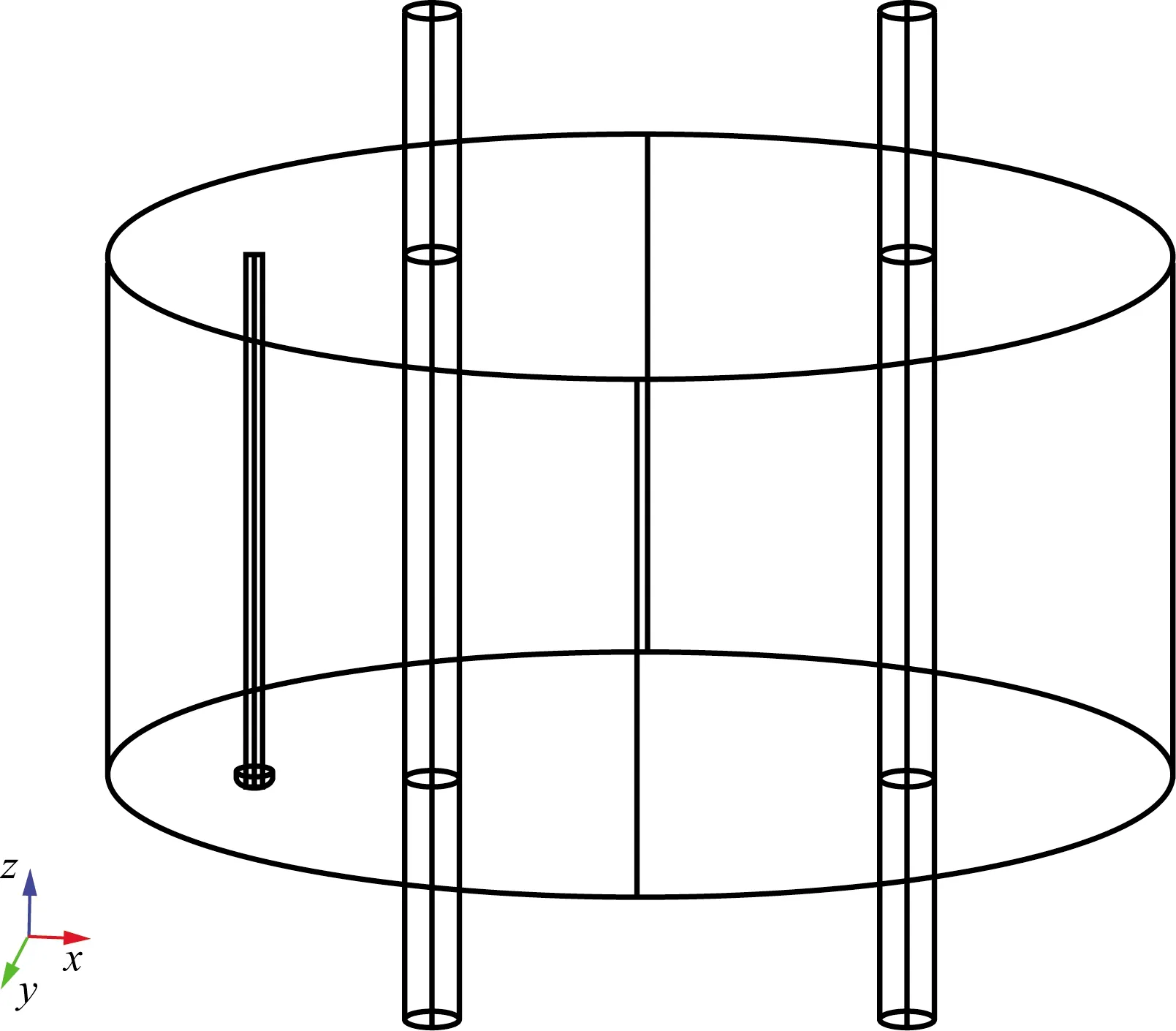
图5 圆柱腔的模型图Fig.5 Model diagram of cylindrical cavity

表1 腔体的主要尺寸参数Table 1 The main dimensional parameters of the cavity

真实的单根碳纤维表面存在许多大小各异、深浅不一的凹槽，其横截面可以近似看作圆形，为了降低仿真计算难度，可以将12×103根碳纤维等效为直径2 mm的圆柱体，假设碳纤维表面光滑，各向同性。图6为腔体两侧加载碳纤维、玻璃管和屏蔽套筒后，不同耦合点对应的圆柱腔谐振频率f0和反射系数S11的仿真值，当d=125 mm时，f0=951 MHz，S11=-45 dB，Zin=50.42+j0.12(Ω)。当微波频率等于圆柱腔谐振频率时，圆柱腔产生谐振现象，输入阻抗虚部可以忽略不计，加入碳纤维后的圆柱腔可以等效为纯电阻[9]。实验结果表明：加入碳纤维后调节耦合点，d=150 mm为最佳耦合点，此时S11=-11.7 dB，f0=920 MHz，输入阻抗实部为87 Ω。

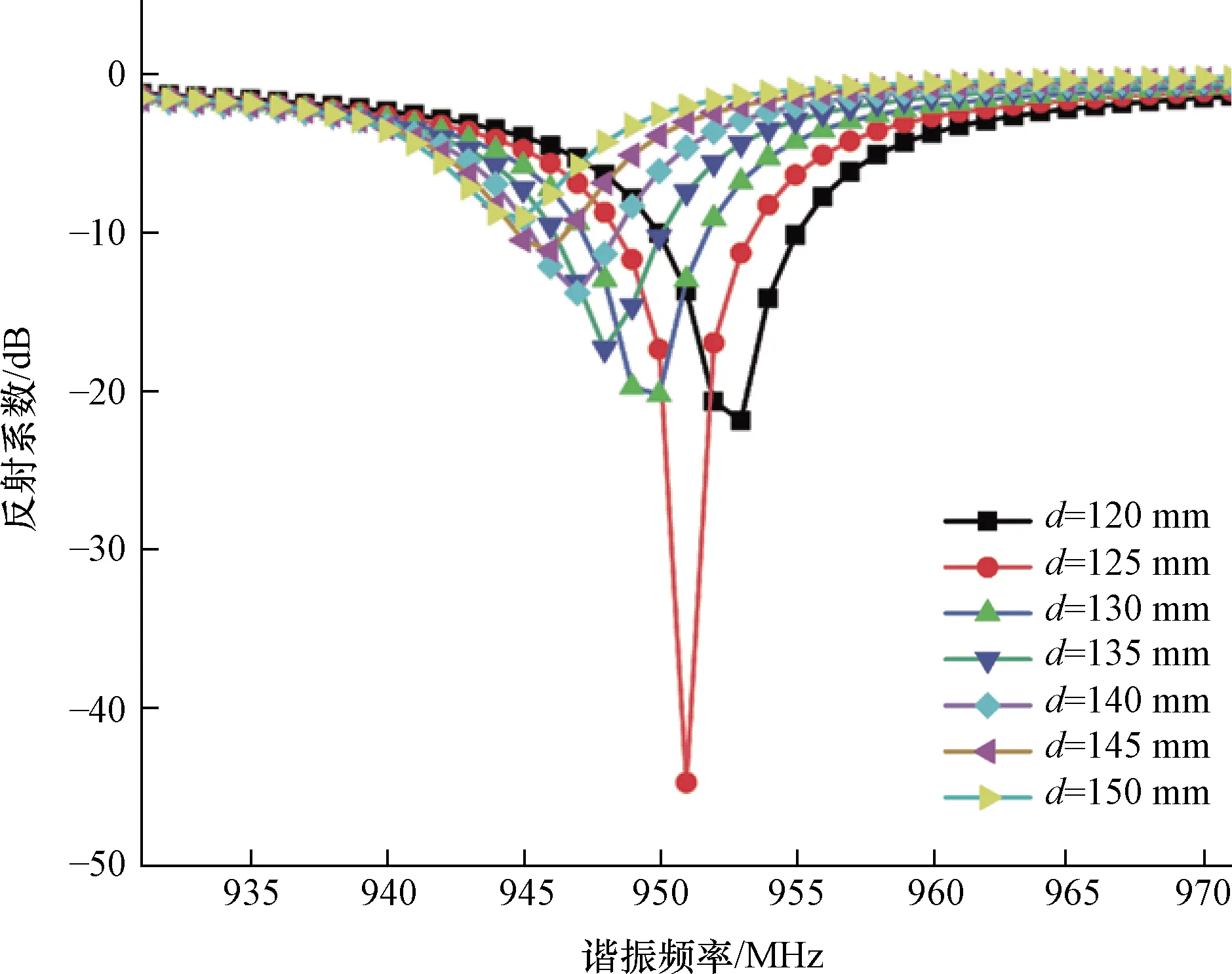
图6 不同耦合点对应的f0和S11Fig.6 Corresponding f0 and S11 at different coupling points

2.2 多物理场的控制方程

将碳纤维等效为各向同性介质，推导麦克斯韦方程组，可以得到介电损耗为各向同性的介质中电磁场的标量传输方程[12-13]。

(4)

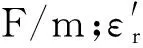
碳纤维在电磁场中由于自身的介电损耗而产生整体加热，这些损耗包含于等效介电损耗因子当中。

(5)

式(5)中：ε″为介电损耗因子，表示碳纤维材料中由于电偶极子振动产生的热损耗；σ为电导率，S/m；ω为角频率；σ/ε0表示传导损耗。

微波加热方程可以由碳纤维的电磁损耗热方程来表示：

Qe=Qrh+Qml

(6)

(7)

(8)

式中：Qe为电磁损耗产生的热量,W/m3;Qrh为电损耗产生的热量，W/m3；Qml为磁损耗产生的热量，W/m3；real表示取复数的实部；J为传导电流密度矢量，A/m2；E*为电场强度矢量的共轭值，V/m；j为虚数；ω为角频率，s-1；B为磁感应强度矢量，T；H*为磁场强度矢量的共轭值，A/m。

碳纤维吸收微波后将其转化为热能，质量为M的碳纤维温度上升率为[3]

(9)

(10)

式中：Qh为碳纤维吸收微波后产生的热量，J；M为碳纤维质量，kg；Cp为恒压热容，J/(kg·K)；T为t时间内碳纤维吸收微波后的温度，K；T0为初始温度，K；Erms为有效电场强度，可以使用量热学法确定，V/m；ρ为碳纤维的密度，kg/m3。

碳纤维中的热传导平衡方程可以表示为

(11)

式(11)中：u为速度场，m/s；λ为导热系数，W/(m·K)。

碳纤维的辐射传热平衡方程可以表示为[14]

(12)

q0=J0-G0

(13)

式中：Q为辐射热源，W；k为波尔兹曼常数，J/K；Acf为碳纤维有效辐射面积，m2；q0为空腔内任意微元面dA的热辐射强度，W/m2；J0为碳纤维表面发出的热辐射强度，W/m2；G0为玻璃管或腔体内壁反射的热辐射强度，W/m2。

2.3 多物理场的耦合仿真与实验

使用COMSOL Multiphysics仿真软件对加入碳纤维负载后的微波加热腔体进行电磁热、非等温层流、固体传热和辐射传热等多物理场的耦合仿真。图7为输入功率387 W时，圆柱腔xz平面的温度场分布，靠近耦合点的左侧碳纤维温度高于右侧，这是由于左侧的碳纤维更靠近耦合点，吸收了更多的微波。

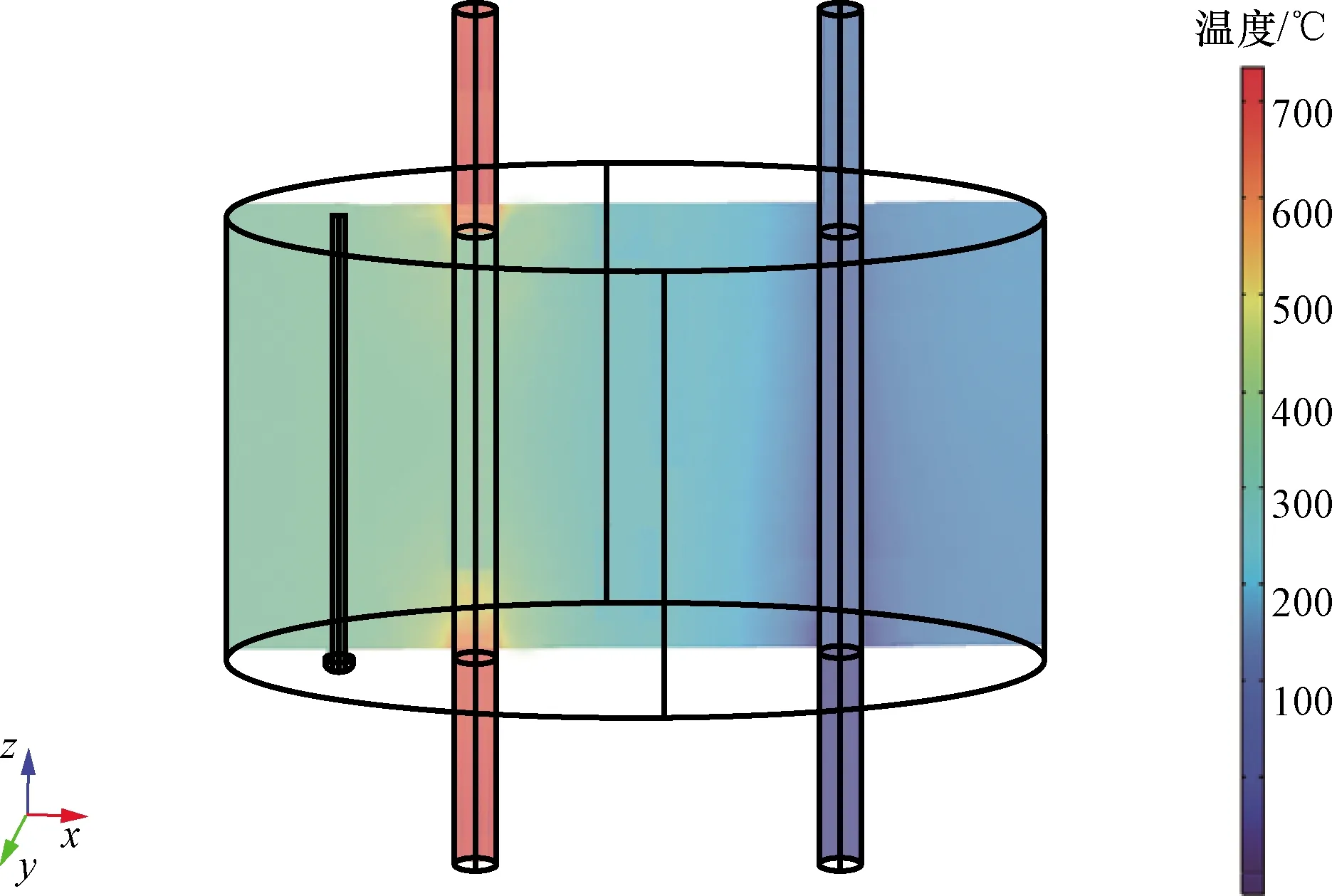
图7 xz平面的温度场分布Fig.7 Temperature field distribution diagram of xz plane

实验采用国产T300碳纤维，温度25 ℃,压强105Pa时，其部分性能参数如表2所示[15-16]。实验中，为了避免碳纤维的高温氧化以及排出石英玻璃管内的空气，需要在玻璃管的入口处通入高纯氮气。通入氮气气流量为5～10 L/min，每次实验改变输入功率后的稳定时间为5 min。在出口的适当位置打孔，使用校准过的红外测温仪透过玻璃管测量碳纤维的表面温度，精度可达1%。

表2 碳纤维的部分性能参数Table 2 The partial performance parameters of carbon fiber

当腔体的入射波功率P>387 W时，测温点附近产生气体击穿现象，导致温度测量结果不准确。图8为输入功率P=387 W时，仿真计算得出的碳纤维表面温度沿长度l方向的一维线性分布图，可以看出在出口处碳纤维的表面温度最高，实验测量出口处碳纤维的表面温度具有一定的实际意义。

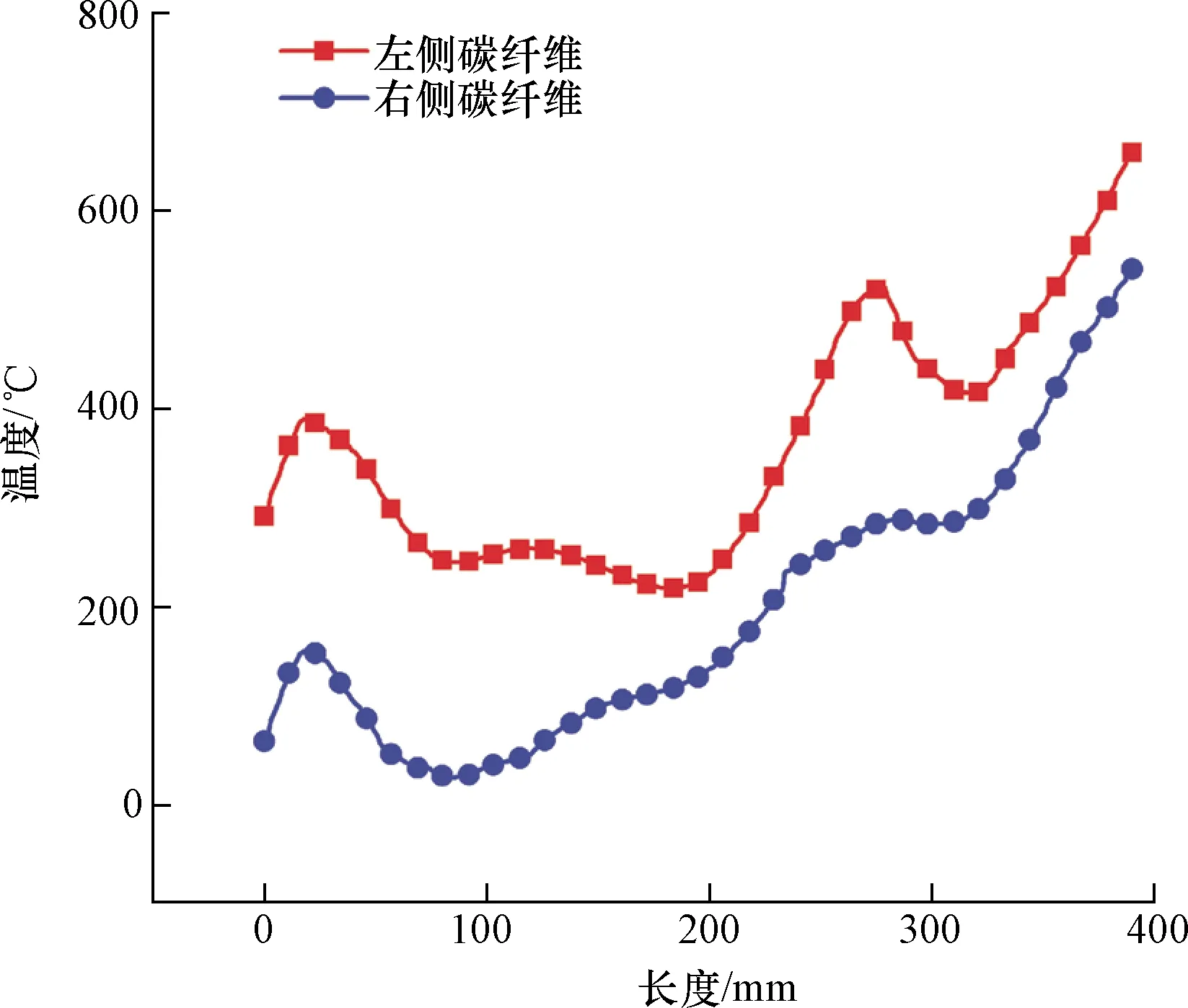
图8 碳纤维表面的线性温度分布Fig.8 Linear distribution diagram of carbon fiber surface temperature

利用中心频率为915 MHz的固态微波源、频谱仪、微波功率计以及加工好的圆柱腔体等设备搭建了一套微波测控系统，测试了不同耦合点对应的腔体谐振频率、反射功率以及出口处碳纤维的表面温度。由于圆柱腔体属于单端口器件，故可用端口的S11参数来表示腔体的反射功率与入射功率之比。腔体的谐振频率以及S11参数测试方法如下：在入射功率一定时，调整腔体的入射波频率，找到最小的反射功率，此时腔体的入射波频率即为腔体的谐振频率，同时记录反射功率和入射功率；出口处碳纤维的表面温度使用非接触式红外测温仪测量，测温范围为300～1 400 ℃。

通过实验测得：耦合点位置d=150 mm时，f0=920 MHz，S11=-11.7 dB，即碳纤维的微波吸收率大于90%。改变入射功率大小，S11总是小于-10 dB，各项参数满足实验要求。

记录入射功率和出口处碳纤维的表面温度，多次重复实验取平均值，结合仿真结果，绘制出图9所示的不同入射功率对应的碳纤维实测和仿真温度曲线。由图9可以看出，靠近耦合点的左侧碳纤维温度的实测值高于右侧碳纤维，与仿真结果一致，这是由于靠近耦合点的左侧碳纤维吸收了更多的微波；随着入射功率的增加，两侧碳纤维温度的实测值和仿真值都以近似线性变化的趋势逐渐升高；微波入射功率387 W时，反射功率27 W，出口处的两侧碳纤维表面温度分别为658、502 ℃；氮气气流量在5～10 L/min变化时气流量对碳纤维温度的影响可以忽略不计，温度越高影响越小。图10为圆柱腔的实物图。

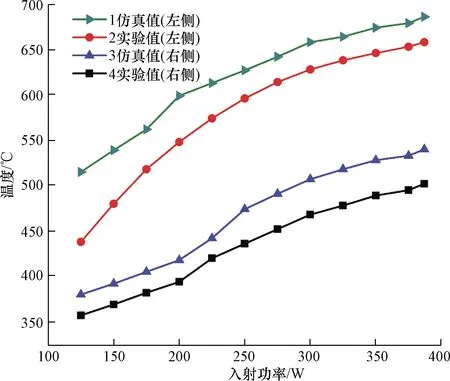
图9 不同入射功率对应的碳纤维实测温度和仿真温度Fig.9 Measured and simulated temperatures of carbon fiber with different incident power

图10 圆柱腔的实物图Fig.10 Physical diagram of cylindrical cavity

3 结论

建立了基于TM110模圆柱腔的三维仿真模型，对其尺寸、耦合点位置、电磁场和温度场分布等进行了仿真分析和优化设计。根据仿真和实验结果，得到以下结论。

(1)空腔内的电磁场分布满足TM110模式，与圆柱腔的理论计算结果一致。

(2)出口处碳纤维的表面温度最高，且靠近耦合点的左侧碳纤维温度高于右侧，随着入射功率的增加，碳纤维表面温度的实验值与仿真值较为吻合，验证了仿真模型的准确性。

(3)当T>394 ℃时，曲线的斜率变大，这是由于装置的气密性不够好，碳纤维与氮气中掺杂的空气发生了氧化反应，加剧了碳纤维的热效应[14]。由式(9)可知，图9中曲线的斜率正比于1/(CpM)，随着温度继续升高，碳纤维的比热容逐渐增大[15]，曲线4的后半段和曲线2的斜率逐渐减小。

(4)当腔体的入射功率P>387 W时，测温点附近产生气体击穿现象，导致测温结果不准确。

为了防止碳纤维的高温氧化，可以采用非接触式迷宫密封装置改善密封性，或在碳纤维中加入少量的硼或磷等措施；微波的气体击穿电场主要与气体压强、气体种类及微波频率等有关，提高微波击穿电场的具体措施有待进一步研究。