基于单值中智VIKOR法的供应商优选模型
刘 庆, 化小会
(1.新乡学院数学与统计学院, 新乡 453003; 2.河南师范大学数学与信息科学学院, 新乡 453007)
随着经济全球化的不断深入,供应链管理(SCM)已经成为在高度竞争的全球经济中提高企业国际竞争力的一个重要因素。在SCM信息系统中关键的问题之一是供应商选择,根据成本、服务、风险等准则,从备选方案中寻找最佳供应商,这是一个复杂的多属性决策(multi-attribute decision making, MADM)问题。近年来,很多学者[1-4]提出了供应商选择的MADM方法类型,但是这些方法都是假设属性信息精确已知,且可以准确评估。然而,因为评估对象的复杂性不断增加,使得决策者在选择过程中很难准确地评估关于其属性的偏好信息。因此,在实际的MADM问题中往往会出现不精确和不确定的评价。在这种情况下,如何有效地处理不确定性或不完整性的信息,已经成为MADM分析中的一个关键问题。目前描述不确定性信息最完备的工具是Smarandache[5]提出的中智集(neutrosophic sets, NS),它具有独立的真值隶属度、不确定隶属度和谬误隶属度,所以可以更准确的描述不完整、不精确、不一致等模糊信息,是对模糊集[6]、直觉模糊集[7]和区间值直觉模糊集[8]概念的一种扩展。但是NS是从哲学观点提出的概念,尽管可以完备的描述性不确定信息,然而一个重要特性是定义在标准或非标准的单位子区间,在实际的工程和科学计算上应用不方便,为了解决这个问题,Wang等[9]引入单值中智集(single-value neutrosophic sets, SVNS),它是NS的子类,其特征是真值隶属度、不确定性隶属度和谬误隶属度定义在标准的单位子区间,可以很方便地应用于实际。近年来,NS与经典的TOPSIS法[10]相结合,在多属性决策问题方面应用很广泛[11-14]。
VIKOR法是Opricovic[15]在1998年首次提出的,它是一种基于理想解的折中排序方法,通过最大化群体效用和最小化个体遗憾来实现有限备选决策方案的最优排序。它的基本思想是先确定正理想解和负理想解,然后根据每个备选方案的取值,选择最接近理想解的方案。虽然VIKOR法与经典TOPSIS方法相似,但Opricovic通过比较两种方法,指出TOPSIS的最优解不一定是最接近理想点解的[16],但是VIKOR法可以克服这种现象。
文献[17]对扩展的VIKOR法与超序方法进行了比较,文献[18]提出了一种基于模糊集理论和VIKOR法的MADM模型来处理供应链系统中的供应商选择问题,文献[19]提出了一种扩展的VIKOR方和TOPSIS法的来解决模糊集信息不确定的MADM问题,文献[20]提出了一种基于VIKOR的犹豫模糊多准则决策方法,但是在单值中智环境下的VIKOR法尚鲜见报道。
为解决上述问题,将VIKOR法推广到单值中智集(NS)环境下,并且用它处理供应商选择问题。首先回顾中智集的相关概念和运算,提出了广义的单值中智集距离,并且给出单值中智环境下的加权平均集结算子;给出VIKOR法的基本思想和处理过程;把VIKOR法推广到单值中智环境下,建立基于单值中智VIKOR法的供应商优选模型;通过一个供应商选择的实例,验证提出模型的有效性和实用性,并进行灵敏度分析,展示决策机制系数的不同取值对备选方案排序的影响,验证模型的灵活性。
1 预备知识
1.1 中智集及单值中智集
定义1设X是一个点(对象)空间,它的任意一个元素用x表示,X上的一个中智集A用一个真值隶属度函数TA(x)、不确定隶属度函数IA(x)和谬误隶属度函数FA(x)来表示,这里TA(x)、IA(x)、FA(x)是]0-,1+[的标准或非标准实数子集[4],即
(1)
且满足0-≤supTA(x)+supIA(x)+supFA(x)≤3+。
需要说明的是非标准有限数1+=1+ε与0-=0-ε中,1和0是标准部分,无穷小数ε>0是非标准部分,称]0-,1+[为非标准的单位子区间,一般来说,其左右边界是模糊的。另外,不确定隶属度函数IA(x)不仅能表示不确定,还可以表示不可靠、不一致、不明确、未知等模糊信息,这就使得处理不确定信息的能力进一步加强。但是在中智集的定义中,隶属度取值于]0-,1+[的标准或非标准的单位子区间,因其边界的模糊性,在科学计算中是非常不方便的,为此学者Wang等[9]改进了中智集的定义,提出了单值中智集,可以方便地应用于工程和科学中。接下来给出一些关于单值中智集的基本定义和运算。
定义2设X是一个给定的论域,X上的一个单值中智集A可以由真值隶属度函数TA(x),不确定隶属度函数IA(x)和谬误隶属度函数FA(x)[9]表示为
A={[x,TA(x),IA(x),FA(x)]x∈X}
(2)
式(2)中:TA(x):X→[0,1],IA(x):X→[0,1],FA(x):X→[0,1]。对∀x∈X,有0≤TA(x)+IA(x)+FA(x)≤3。
论域X上的单值中智集A中的元素,称为单值中值数SN,记为[TA,IA,FA]。论域X上全体单值中智集的集合记为SS。
设A为定义在论域X上的一个SS,当X连续时,A可表示为
(3)
当X离散时,A可表示为
(4)
1.2 单值中智集的相关运算
中智集和单值中智集作为模糊集、直觉模糊集的推广,有三个隶属度,也有不同于FS和IFS的运算和性质,文献[9,21-22]给出单值中智集的相关运算和性质。
定义3设A和B是论域X上的两个SS,则对∀x∈X,定义如下。
(1)A是B的子集,即:A⊆B⟺TA(x)≤TB(x),IA(x)≥IB(x),FA(x)≥FB(x)。
(2)A和B满足A=B⟺A⊆B且B⊆A。
(3)A的补集记作Ac,且满足TAc(x)=FA(x),IAc(x)=1-IA(x),FAc(x)=TA(x)。
(4)A∪B={max(TA(x),TB(x)],min[IA(x),IB(x)],min[FA(x),FB(x)]}
A∩B={min(TA(x),TB(x)],max[IA(x),IB(x)],max[FA(x),FB(x)]}
定义4设A和B是论域X上的两个SVNS,则对∀x∈X,∀λ∈R且λ>0,有:
(1)和运算:A⊕B=[TA(x)+TB(x)-TA(x)TB(x),IA(x)IB(x),FA(x)FB(x)]。
(2)积运算:A⊗B=[TA(x)TB(x),IA(x)+IB(x)-IA(x)IB(x),FA(x)+FB(x)-FA(x)FB(x)]。
(3)数乘运算:λA={1-[1-TA(x)λ)],IA(x)λ,FA(x)λ}。
定义5设A1,A2,…,An是论域X上的n个单值中智数,记Aj=[TAj,IAj,FAj]的权重为wj(j=1,2,…,n),单值中智集的加权平均集结算子定义为
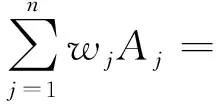
(5)
1.3 两个单值中智集的距离
文献[21]研究了单值中智集的距离、相似度量和熵,接下来推广单值中智集的距离概念,给出广义的单值中智集的距离公式。
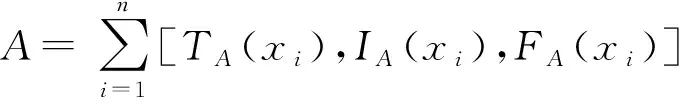
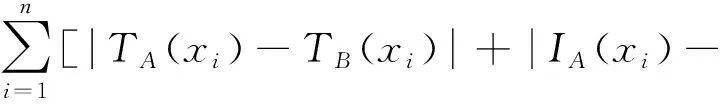
IB(xi)+FA(xi)-FB(xi)]/3n,i=1,2,…,n
(6)
其标准化的Euclidean距离为
(7)
这里的Hamming距离和Euclidean距离都考虑了真值隶属度、不确定隶属度、谬误隶属度,在此基础上推广两个SVNSs的距离公式,给出两个Ss广义的距离公式。


IA(xi)-IB(xi)p+FA(xi)-

(8)
如果取p=1,式(8)就退化为定义6中Ss的标准化Hamming距离公式[式(5)];如果取p=2,式(8)就退化为定义6中Ss的标准化的Euclidean距离公式[式(7)]。
2 经典VIKOR法
VIKOR法是学者Opricovic于1998年首次提出的一种处理MADM问题的最佳优化妥协方法,侧重于从一组备选方案中进行排序和选择,并针对属性冲突的问题确定折中的解决方案,给出一个或者多个折中的方案,从而做出最终决策。考虑具有m个备选方案Ai(i=1,2,…,m)和n个属性Cj(j=1,2,…,n)的MADM问题,有t位决策专家进行评价,从备选方案中选出最优决策方案。经典VIKOR法的处理步骤如下:
步骤1构造m行n列的决策矩阵D=[aij]m×n。
步骤2确定每个属性对应的权重wj(j=1,2,…,n)。
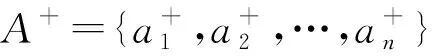
步骤4计算群体效用值Si和个体遗憾值Ri:
(9)
(10)
式中:Si为第i个备选方案的群体效用值,Ri为第i个备选方案的个体遗憾值。
步骤5计算各备选方案的利益比率(又称折中评价值)Qi:
Qi=v(Si-S*)/(S--S*)+(1-v)(Ri-R*)/(R--R*)
(11)
式(11)中:S*=miniSi;S-=maxiSi;R*=miniRi;R-=maxiRi;v∈[0,1]相当于一个权重,称为决策机制系数或最大群体效用权重。
步骤6对Si、Ri和Qi进行排序并确定最终方案。
3 基于单值中智VIKOR法的供应商优选模型
供应商选择是供应链管理中的一个重要问题,本质上是一个多准则决策问题,供应商的选择高度依赖于专家的评估。在这一过程中,由于人的主观判断能力的不足,不可避免地涉及各种类型的不完整、不全面、不精确、不一致等模糊信息等,现有的方法无法充分处理这些类型的不确定性,然而单值中智集有三个隶属度,可以较好地描述模糊信息,接下来把VIKOR法推广到单值中智环境下来处理,建立基于单值中智VIKOR法的供应商优选模型。
3.1 MADM问题的语言变量
供应商选择问题本质上是一个MADM问题,在MADM问题中,对决策专家和属性的评价一般都采用语言变量给出,它是一种变量,其值用描述性的语言表示,而不是以数字为特征。比如,可以用非常重要、重要、中等、不重要、非常不重要等语言术语来描述对专家和属性的评价。在实际中,为了保证评价的中间值接近0.5,其他值比较对称。语言术语的数量一般都取奇数,如常见的5级、7级、9级、11级语言变量。在模糊集环境、直觉模糊集环境以及Vague集环境下很多学者都给出了语言术语对应的模糊数、直觉模糊数以及Vague值的对应关系。
从定义3和文献[21]可知,单值中智数〈TA,IA,FA〉的最大值是〈1,0,0〉,最小值是〈1,0,0〉,单值中智数的大小要考虑真值隶属度TA、不确定隶属度IA和谬误隶属度FA,评价越好,则真值隶属度TA越大,不确定隶属度IA和谬误隶属度FA越小。反之真值隶属度TA越小,不确定隶属度IA和谬误隶属度FA越大,接下来给出单值中智环境下的语言术语及其对应的单值中智数,如表1所示。
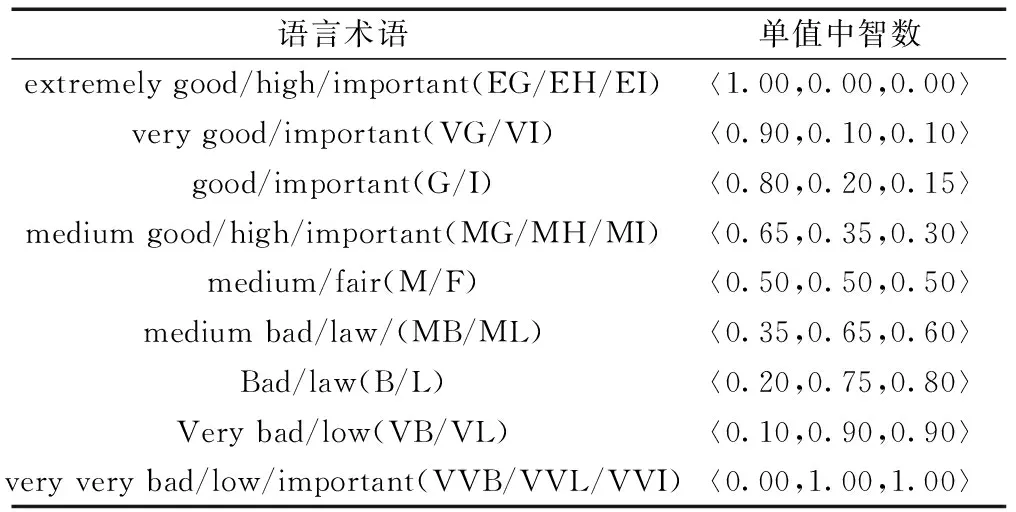
表1 用SN对决策专家和属性进行评级的语言术语Table 1 Linguistic terms for rating of decision makers and attribute index with SN
3.2 基于单值中智VIKOR法的供应商优选模型

步骤1确定每位决策专家的权重。
首先确定各位决策专家的重要程度,根据表1确定每位决策专家评级的单值中智数,假设第k位决策专家对应的单值中智数是Ek=〈Tk,Ik,Fk〉,则根据文献[21],第k位决策专家的权重为
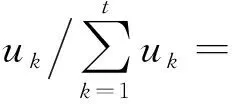
(12)

步骤2确定属性指标的权重。
确定出各位决策专家的权重以后,每位决策专家要通过语言变量对m家备选供应商Ai(i=1,2,…,m)的n个属性进行评价,并给出对应的单值中智数,组成m行n列的属性指标评价矩阵。对模糊信息不确定程度度量的常用方法是熵权法[5-6],因为语言变量的不确定性,需要用熵权法确定n个属性指标的权重,这里给出单值中智集的熵权法来确定属性权重。
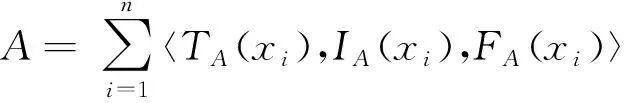

IA(xi)-IAc(xi)}/n
(13)
在对m家供应商的n个属性进行评价的过程中,每位决策专家给出的不同属性所起作用重要程度也是不一样的,如果属性Cj可以用单值中智数Aj表示,则每个属性指标的权重wj计算方法如式(14)所示:
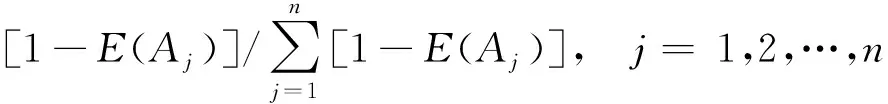
(14)
从而到属性指标的权重向量w=(w1,w2,…,wn)。
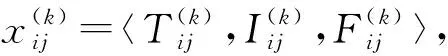
(15)
步骤4集结所有的单值中智决策矩阵D(k),构建综合中智决策矩阵D。
利用定义5中给出的式(4),对所有单值中智矩阵与每位决策专家的权重ek进行集结,构建综合中智决策矩阵如下:
(16)
步骤5确定单值中智数的正理想方案A+和负理想方案A-。
(17)

(18)
式中:i=1,2,…,m;j=1,2,…,n。

步骤6分别计算单值中智环境下每家供应商的群体效用值Si和个体遗憾值Ri:

(19)
(20)
式中:wj为步骤2中得到的属性指标Cj权重,j=1,2,…,n。
步骤7综合考虑最大化群体效用同时最小化个体遗憾,计算各家供应商的折中评价值Qi:
Qi=v(Si-S*)/(S--S*)+(1-v)(Ri-R*)/
(R--R*)
(21)
式(21)中:S*=miniSi;S-=maxiSi;R*=miniRi;R-=maxiRi;决策机制系数v∈[0,1],相当于一个权重,称为决策机制系数或最大群体效用权重,用来权衡Si和Ri之间的比例。v的不同,说明了考虑侧重点的不同,调节v的取值,可以综合调节最大群体效用和最小个体遗憾,得到的排序方式更符合实际。若v>0.5,则表示根据最大化群体效用进行评价;若v<0.5,则表示根据某一属性指标或者说是最小化个体遗憾进行决策;若v=0.5,则表示根据折中均衡的方式进行决策,也就是考虑全部属性指标的同时又照顾某一属性指标的影响。
步骤8对Si、Ri和Qi按照升序排序并确定最佳供应商。

准则1优势准则。
(22)
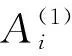
4 实例分析
4.1 基于单值中智VIKOR法的供应商优选模型算例分析
近年来,全球经济发展和公共卫生受到碳排放增加的威胁,这促使世界各地的企业和政府试图刺激和增加对低碳和绿色经济的投资。在这个决策过程中,一个关键阶段是在低碳供应链中选择合适的绿色供应商。这个过程涉及不确定信息的各种因素,所有这些因素都必须同时考虑和评估。因此,绿色供应商选择是一个非常复杂的模糊决策过程。低碳供应链管理领域的3位决策专家被邀请来评估和选择一家低碳供应商,从4家潜在供应商Ai(i=1,2,3,4)中按照低碳技术C1、成本C2、风险因素C3、和能力C4等4个属性对供应商进行评估,选出最佳供应商。3位决策专家Dt(t=1,2,3)的集合记为D={D1,D2,D3},4家潜在的供应商Ai(i=1,2,3,4)组成备选方案集A={A1,A2,A3,A4},4个属性Cj(j=1,2,3,4)组成属性集C={C1,C2,C3,C4},利用前面建立的单值中智VIKOR法的供应商优选模型,找出最佳的供应商。
步骤1确定每位决策专家的权重。根据决策专家的能力和水平,用语言变量对3名决策专家进行评价,通过表1确定对应的单值中智数,如表2所示。

表2 决策专家重要程度的SN表示Table 2 Importance of decision makers expressed with SN
然后通过式(11)和表2,计算出3位决策专家的权重向量e=0.378,0.342,0.280。
步骤2确定属性指标的权重。3名决策专家利用表1给出的语言术语分别对低碳技术(C1)、成本(C2)、风险因素(C3)、和能力(C4)等4个属性进行评级,评估的结果如表3所示。

表3 3名决策专家对属性权重的评估Table 3 Assessments of attribute weights given by four decision makers
利用式(12)、式(13)、表3可以求出各属性的权重向量w=(0.339,0.121,0.306,0.234)
步骤3每个决策专家给出单值中智决策矩阵。3位决策专家Dk(k=1,2,3)对4家潜在供应商Ai(i=1,2,3,4)的4个属性Cj(j=1,2,3,4)通过表1给出的语言变量进行评价,得到表4。

表4 3名决策专家对4家供应商的语言评价信息Table 4 Evaluation information of four suppliers by three decision experts
根据表4,可以得到3名决策专家的单值中智决策矩阵D(k)(k=1,2,3),如式(23)~式(25)所示:

(23)
(24)
(25)
步骤4集结3组单值中智决策矩阵D(k),构建综合中智决策矩阵D。
利用定义5给出的单值中智加权平均集结算子公式[式(4)],把3组单值中智决策矩阵D(1)、D(2)、D(3)与专家权重e=(0.388,0.342,0.280)进行集结,构建综合中智决策矩阵如式(26)所示:

(26)
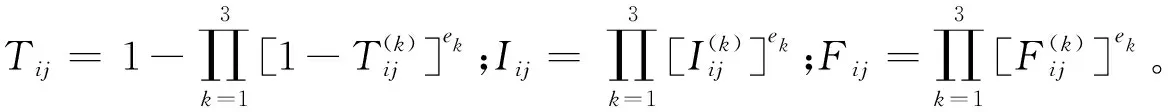
步骤5确定单值中智数的正理想方案A+和负理想方案A-根据式(17)、式(18)和综合单值中智决策矩阵,可得:

(27)
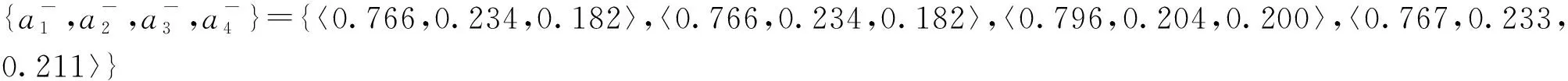
(28)
步骤6分别计算单值中智环境下每家供应商的群体效用值Si和个体遗憾值Ri。
由广义的单值中智集距离公式[式(8)]、式(20)、式(21)可以计算4家供应商的群体效用值Si和个体遗憾值Ri。距离公式采用定义7中的式(8),可以验证p的取值不影响排序的顺序,这里为了运算简便,取p=2。如表5所示。
步骤7综合考虑最大化群体效用同时最小化个体遗憾,计算各家供应商的折中评价值Qi。
由式(18)~式(20)求出各家供应商的折中评价值Qi,在本例的单值中智VIKOR法中,选取v=0.5,意味着以决策专家协商达成共识的折中方式选择最佳供应商。计算结果如表5所示。

表5 4家供应商的Si、Ri和QiTable 5 The Si,Ri and Qi of the four suppliers
步骤8对Si、Ri和Qi分别按照升序排列并确定最佳供应商。
根据Si、Ri和Qi的数值大小对备选供应商进行升序排列,得到3组排序序列Srank、Rrank和Qrank,如表5所示。根据折中评价值Qi的排序得到备选供应商优先顺序为A3>A2>A4>A1,可得最佳供应商为A3。下面验证是否满足两个可接受准则。

准则2稳定性准则。因为A3在Srank排名也是第1,说明满足稳定性准则。
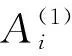
需要说明的是Qi的最大值为1,说明群体和个体都认为A1最弱供应商。
4.2 灵敏度测试
在前面的单值中智VKIOR法实例计算中,对决策机制系数v的取值按照折中办法取0.5,很多情况下,v的取值不同,折中方案的排序也不同,特别是优势准则不满足的情况下,不同的决策机制系数将会对应不同的优选方案。接下来通过对决策机制系数v设置不同的取值进行灵敏度测试(每间隔0.1取一个值),如图1、图2所示。

图1 供应商折中评价值Qi变化情况Fig.1 Changes in supplier’s tradeoff valuation Qi
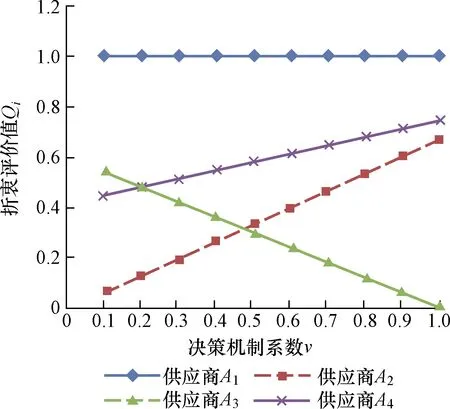
图2 供应商Ai排序变化情况Fig.2 Changes in supplier ranking
从图1、图2可以看出,当v≤0.47时A2为最佳供应商,v>0.47时,A3为最佳供应商,一直保持稳定并且满足可接受准则2,随着决策机制系数v逐步靠近最大值1,A3性能越来越好,优势性越来越明显。测试结果表明,排序结果对决策机制系数(最大群体效用权重)v的变化具有敏感性,同时在某个范围内也具有一定的稳定性。进一步说明了建立的模型具有灵活性、实用性、有效性。在实际的决策过程中,如果重视最大化群体效用同时兼顾最小化个体遗憾,决策机制系数就在0.5附近取值,如果对某一个体考虑较多,可以调节最大群体效用权重v的取值。
5 结论
针对供应商选择问题,把经典的VIKOR法应用到单值中智环境下,提出了一种基于单值中智VIKOR法的供应商优选模型,主要贡献有:①推广了两个单值中智集的距离公式,提出了广义的单值中智距离公式,并将其应用单值中智VIKOR法的模型中;②建立了单值中智环境下的VIKOR模型,并通过实例分析验证了模型的有效性;③对模型进行了灵敏度测试,通过改变决策机制系数进行灵敏度分析,进一步验证了模型的灵活性、实用性和稳定性。本文方法为多属性决策问题提供了一种新的观点,且更通用、更准确。在未来的研究中,如果可以建立计算模型,借助电算化程序,扩大备选方案的范围,这样选择的方案效果更优秀,在未来的研究中将会进一步考虑。

