混合磁悬浮隔振平台径向磁力模型研究

甘淘利，宋春生，2，丁成苗

(1.武汉理工大学 机电工程学院，湖北 武汉 430070；2.湖北省磁悬浮工程技术研究中心，湖北 武汉 430070)

空间实验站为材料科学和生物科学的研究提供了微重力的环境[1]，但空间站广泛存在的低频微扰动对精密仪器的使用及空间站科学实验结果的准确性有较大影响[2]。隔振技术对维持空间站微重力环境的稳定至关重要，传统的被动隔振技术对高频信号有较好的抑制作用，但对低频扰动的控制效果不好，甚至会加大振动的幅值，而且被动隔振平台的质量往往比较大，不适用于空间站微重力环境的条件。磁悬浮隔振是一种主动式的隔振技术，通过产生主动控制的磁场，它将被隔振对象与基座隔开而不发生接触，同时能抵消扰动力以达到隔振的目的，对低频微振动有很好的抑制效果。

文献[3]采用等效原则得到了永磁导轨与悬浮永磁体和悬浮电磁铁之间的磁力解析模型，经实验验证了模型的准确性。文献[4]基于永磁环间隙的磁能及磁导，通过虚功原理法，推导了轴向磁化的双环永磁轴承轴向磁力的数学模型，并进行了试验验证，模型计算值与实验值较为吻合。文献[5]采用磁场分割的方法，将一个典型磁路的气隙磁场分割成数个形状不同的磁通管，并计算了各磁通管的磁导，继而得出了整个磁路的磁导，最后用有限元方法验证了磁导计算模型的准确性，为磁场模型的建立提供了有效工具。文献[6]采用有限元方法建立了一种轴向混合磁悬浮轴承的磁场模型。文献[7]采用等效磁路法，基于漏磁导分析方法，建立了混合磁悬浮轴承承载力数学模型，并分别采用有限元仿真和实验方法对修正后的模型进行了验证。

综上所述，目前对建立磁场模型的研究多集中在小气隙(气隙较小，如磁悬浮飞轮电池，气隙长度为0.3～0.6 mm)范围，且大多是基于以下假设：①只考虑空气的漏磁，忽略其他的漏磁；②磁场在材料中均匀分布，不考虑磁场饱和情况[8]。而缺少对大气隙(气隙较大，如风力发电机，气隙长度为2～10 mm)情况的研究，尤其是对于建立气隙大于20 mm的磁场模型的研究几乎没有。因此，需要研究大气隙情况下磁悬浮平台的受力特性，以推广磁悬浮隔振技术在大气隙场合的应用。

笔者设计了一种混合磁悬浮隔振平台，针对平台大气隙的特点，基于气隙磁场分割原则，将气隙磁场分割为数个不同形状的磁通管，通过计算各磁通管的磁导，建立该混合磁悬浮支承结构的等效磁路模型，得到气隙磁能的表达式，并利用虚功原理法获得混合磁悬浮隔振平台悬浮结构的径向磁力解析模型。

1 混合磁悬浮隔振平台结构及工作原理

混合磁悬浮隔振平台模型如图1所示，主要由底座、定子磁环、悬浮平台、电磁铁、霍尔传感器及电控系统等组成，具体参数如表1所示。

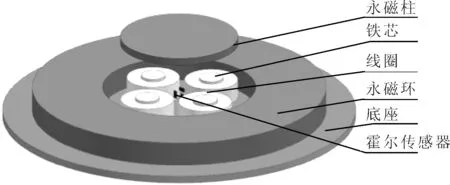
图1 混合磁悬浮隔振平台模型

表1 混合磁悬浮隔振平台结构参数

定子磁环与悬浮平台均为轴向充磁，且充磁方向相同的永磁体，定子磁环与悬浮磁柱之间的轴向斥力克服悬浮部分的重力。电磁铁与悬浮磁柱之间产生吸力平衡径向的干扰及永磁体间的径向分力。

该混合磁悬浮隔振平台的工作原理是：在定子磁环与悬浮磁柱之间的气隙中，两永磁铁各自产生封闭的磁路回路，且在两条磁路接近处磁场方向相同，轴向产生斥力，克服悬浮部分的重力；当悬浮磁柱受到水平方向的干扰时，位于下方的霍尔传感器检测到磁场强度的变化，输出电流信号给控制器，经差分放大后，控制线圈中的电流产生控制磁通，对悬浮磁柱表现为反方向的吸力并将其拉回到平衡位置，电磁铁的控制原理如图2所示。

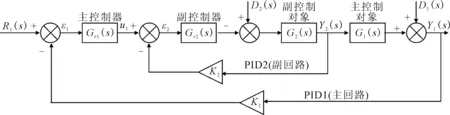
图2 串级PID控制原理框图

在电磁铁串级PID控制系统中，位置环为主回路，加速度环为副回路。当被隔振物体在平台上产生一个水平方向的加速度扰动时，加速度控制器(副控制器)根据偏差信号的变化，控制电磁铁对平台产生一个反向的吸力，抵消平台的惯性运动；被隔振物体的加速度扰动会使平台发生水平移动，位移控制器(主控制器)通过主回路传递的偏差信号调节加速度控制器的初值，而加速度控制器根据接收位移控制器的输出信号，以及加速度传感器的测量值，对副控对象进行控制，使被控对象的加速度跟踪设定值变化，并根据平台的位移及时调整，最终使隔振平台回到平衡位置。

2 悬浮平台径向磁力数学模型

混合磁悬浮隔振平台是典型的强耦合、非线性系统，建立悬浮磁柱精确的数学模型是实现平台稳定控制的关键。悬浮磁柱轴向受定子磁环的永磁斥力随轴向气隙的变化而变化，若悬浮部分的质量在系统可承受范围内，其可以由永磁铁间的轴向斥力自发抵消；水平方向同时受定子磁环和电磁铁的吸力，国内外对电磁铁与永磁柱磁力模型的研究很多，缺乏对永磁环与永磁柱之间磁力模型的研究，尤其是本文研究的隔振平台具有大气隙的特点，对其磁力模型的建立提出了较高的要求。

利用有限元仿真软件对定子磁环和浮子磁柱进行静磁场仿真分析，永磁柱与永磁环磁力线分布如图3所示。从图3中可看出，①两个小环：磁环→气隙→磁环，磁柱→气隙→磁柱，产生排斥力；②大环：磁环→气隙→磁柱→气隙→磁环，产生吸引力。

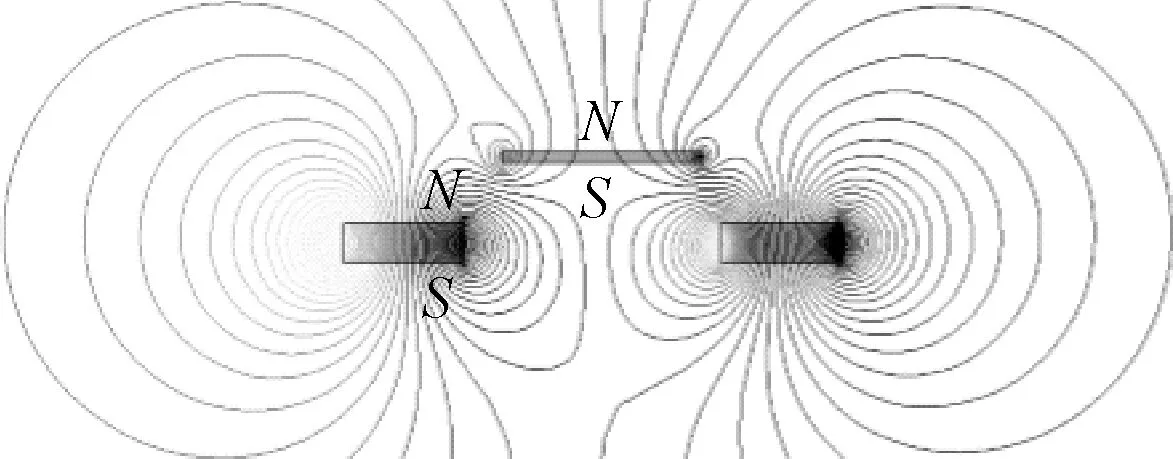
图3 永磁柱与永磁环磁力线分布

根据磁力线的分布规律，遵循磁场分割的原则[9]，将整个气隙磁场分割成多个具有简单几何形状的磁通管，分割后的磁通管模型如图4所示(以左侧磁通管模型为例)。

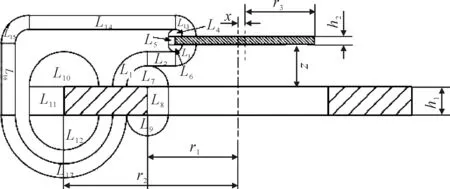
图4 左侧磁通管模型

从图4中可看出，气隙磁导部分，L1～L3、L13～L17串联，是悬浮磁柱受力的主磁通，L4～L12为漏磁通，同理可得右侧磁导的串并联关系。根据磁通管的串并联关系，建立气隙磁场的等效磁路模型，如图5所示。

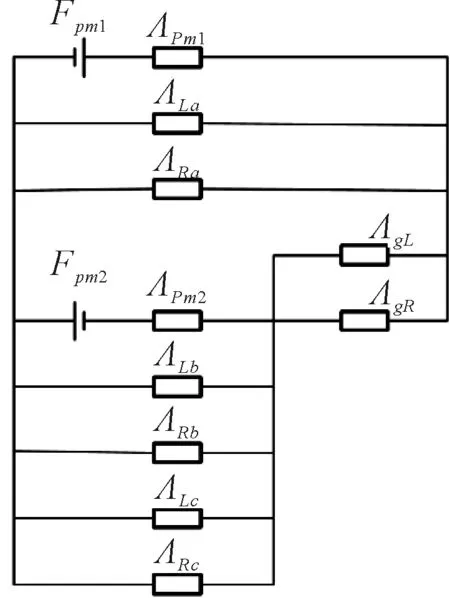
图5 等效磁路图

以左侧磁通管模型为例，计算各磁通管的磁导，由于磁通管L13～L17的磁力线较稀疏，因此在计算时不考虑外侧的磁导。图4中的L1、L4为1/4个空心圆柱体，磁力线绕轴线，L2为1/2个空心圆柱体，磁力线绕轴线，L4、L6、L7、L9、L10、L12为1/2个实心圆柱体，磁力线绕轴线，L5、L8、L11为1/2个空心圆柱体，磁力线沿轴向，根据磁导计算公式[10]得L1～L12的磁导为：

左侧气隙磁导及漏磁导为：

(2)

定子磁环和悬浮磁柱的磁势分别为：

FPm1=Hch2

(3)

FPm2=Hch1

(4)

根据有关文献[10]关于永磁体磁导计算公式知悬浮磁柱磁导及定子磁环磁导分别为：

(5)

(6)

式中：μr为永磁材料的相对磁导率，值为1.1；μ0为真空磁导率，值为4π×10-7H/m。

气隙磁能为：

(7)

其中：

(8)

由于气隙磁通φg变化很小，同时为了模型的简化，假定φg为常数。由虚功原理法得到悬浮磁柱径向磁力为：

(9)

3 径向磁力数学模型验证

为验证悬浮磁柱径向磁力数学模型的准确性，采用ANSYS Maxwell软件对该混合磁悬浮隔振平台进行了验证。使用一种常用的误差评估方法为：

(10)

其中：

E=∑((Ft(x)-Fs(x))2)

(11)

T=∑((Fs(x)-mean(Fa(x)))2)

(12)

式中：Ft(x)、Fs(x)分别为理论计算的径向磁力和仿真分析的径向磁力；mean(Fs(x))为仿真分析的径向磁力的平均值；S为两条曲线的相似度，值越接近于1，则两条曲线越相似，则说明误差越小。

图6为采用等效磁路法建立的数学模型的计算结果与ANSYS Maxwell计算结果的比较。

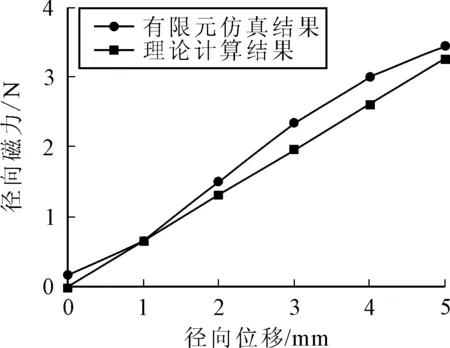
图6 径向磁力比较(z=30 mm)

从图6中可知，在大气隙情况下(z=30 mm)，利用分割磁场法计算气隙磁导，并基于虚位移法建立的悬浮磁柱径向磁力数学模型取得了较好的计算精度。

为深入研究该模型对气隙大小的适用范围，笔者对轴向间隙分别为z=(40、42、44、46)mm时理论计算结果与ANSYS Maxwell仿真结果进行对比，结果如图7和表2所示。

图7 不同气隙大小下径向磁力比较(z>30mm)

表2 不同轴向气隙下径向磁力计算误差对比(z>30 mm)

从图7和表2可知，轴向气隙大于30 mm时，理论计算的误差随气隙的增大而逐渐变大，但都在10%以内，满足工程允许的误差范围内；当轴向气隙为46 mm时，误差大于10%，但承载力接近零，而悬浮磁柱自身的重力作用使得轴向气隙小于46 mm。因气隙过大，漏磁严重，导致仿真结果中径向永磁力与径向位移没有明显的函数关系，但随位移变化的上升趋势与理论计算结果相同。因此，在正常的工作条件下，理论计算结果相较于仿真结果的误差控制在10%以内，表明所建立的径向磁力数学模型能较好地模拟悬浮磁柱在径向所受的永磁力大小。

根据ANSYS Maxwell仿真结果可知，在轴向气隙z=30 mm时，承载力达到了30 N，并随轴向气隙的减小而增大。因此，为了扩展笔者设计的混合磁悬浮隔振平台的适用范围，急需研究更大承载力(即轴向气隙小于30 mm)情况下，该数学模型的精确性。图8和表3分别表示在轴向气隙z=(20、25、26、28)mm时理论结果与ANSYS Maxwell仿真结果的数据比较和误差大小。

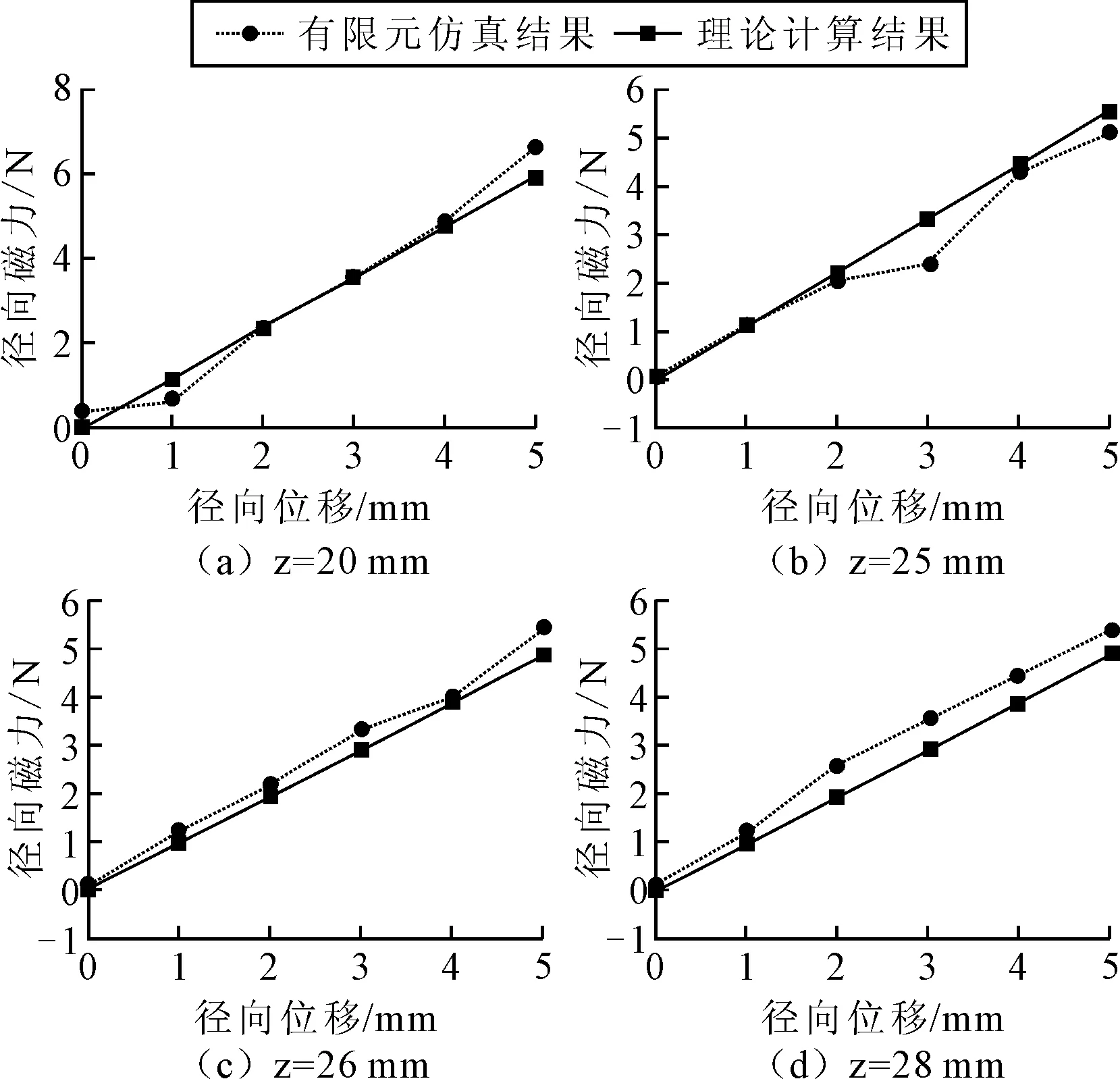
图8 不同气隙大小下径向磁力比较(z<30mm)

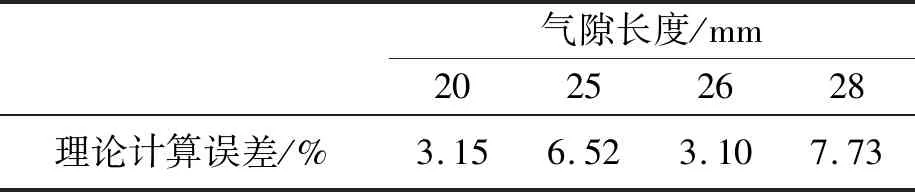
表3 不同轴向气隙下径向磁力计算误差对比(z<30 mm)

从图8和表3可知，气隙大小在20～30 mm区间时，理论计算结果与仿真结果的误差控制在10%以内，表明所建立的径向磁力数学模型在轴向气隙小于30 mm的情况下适应性较好，但模型的计算精度与悬浮磁柱的轴向气隙大小及径向位移的大小有关。

因此，所提出的基于隔振平台永磁体磁力线分布，采用分割磁场法创建等效磁路模型，利用虚位移法建立的悬浮磁柱径向磁力数学模型能满足大气隙条件下的计算要求。

4 结论

针对常规磁路法在大气隙情况下建模精度差的问题，在一种具有大气隙的混合磁悬浮隔振平台基础上，建立了平台径向磁力模型，为大气隙磁场建模提供了研究基础。结果表明：所提出的建模方法在20 mm≤z≤46 mm的轴向气隙内，误差控制在10%以内，满足工程实际要求，验证了所提出的大气隙磁场建模方法的可靠性和适用性。