基于AHP与模糊评价模型的高校创新竞赛研究

杨湘华 周大勇 洪治 龙海威

摘要：利用层次分析法（AHP）和模糊数学评价方法构建数学模型，经过数据处理和建模分析，对国内影响力较大的十项高校创新竞赛等级进行了定量排名。同时根据最大隶属度原则，以全国大学生数学建模竞赛和智能汽车竞赛为例，给出了学生参与这两项竞赛后在能力方面获益程度的定量分析，为在校大学生更好参与创新竞赛提供了参考。

Abstract： This paper adopted analytic hierarchy process （AHP） and fuzzy mathematics evaluation method to build a mathematical model. After data processing and modeling analysis， it ranked ten influential university innovation competition levels in China. At the same time， according to the principle of maximum membership， the paper obtained a quantitative analysis of the benefits of students' participation in these two competitions and provided a reference for college students to participate in innovation competitions.

关键词：创新竞赛;极差法;AHP方法;模糊数学评价

Key words： innovation competition;range method;AHP method;fuzzy mathematics evaluation

中图分类号：O141.4;G642                            文献标识码：A                                  文章编号：1006-4311（2020）17-0052-03

0  引言

随着国家对于创新创业活动的大力支持，各高校在创新创业活动方面蓬勃开展，此活动对深化高等教育综合改革，激发大学生的创造力，培养造就“大众创业、万众创新”的生力军发挥了重要作用[1]。目前国内省级以上的创新竞赛达三十多个，但通过定量分析各竞赛排名引导高校大学生选择和参与各竞赛的研究较少，为提供一种性价比最高的赛事选择方案，本文利用层次分析法（AHP）和模糊数学评价方法建立模型[2]，将评价指标分为具体和抽象两大类，分别针对竞赛本身价值和参赛选手在能力方面获益程度进行分析研究。对于具体指标，采用层次分析（AHP）赋权相应评价指标的权重。经数据处理，对主要列举的十大高校创新竞赛进行等级排名。依据调研数据，建立单因素评价矩阵，通过计算得到综合评价矩阵，根据最大隶属度原则[3]，得出学生参加某项竞赛对于个人能力提升的获益程度。在对抽象指标进行分析时，以国内极具代表性的两大比赛作为分析样本，得到学生能力提高获益程度的定量分析结论。

1  AHP方法与模糊评价方法建模

1.1 模型准备与模型假设

利用互联网搜集待评价竞赛的数据，保持数据的合理性。挑選出最能体现比赛价值的指标，最大程度规避因数据不足引起的错误。在问卷调查结果中，部分样本数据存在一定不真实性，为确保样本数据的准确性和真实性，对样本数据预处理，成为新的待分析样本数据。在此基础上对竞赛综合分析，全面且客观地评价竞赛水平和学生能力。

①假设数据舍入、截尾时产生的误差忽略不计;

②假设经过数据预处理后的数据均为准确数据;

③假设竞赛数据波动对模型求解无影响;

④假设问卷调查真实反映能力的提高情况。

1.2 符号说明

■

1.3 层次分析法（AHP）模型

1.3.1 建立层次分析模型架构

应用AHP分析问题时，首先，按问题“条理化、层次化”原则进行分析处理构造层次结构模型[2][4]。在此模型下，将复杂问题划分为若干元素，根据它们的属性与关系形成若干层次。

目标层：竞赛排名。

准则层：B={bi}={参赛人数、资金投入、竞赛天数、获奖比率、专家组人数}。

方案层：C={Ci}={全国大学生数学建模竞赛，ACM国际大学生程序设计竞赛，“互联网+”大学生创新创业竞赛，“挑战杯”全国大学生创新创业大赛，“西门子杯”中国智能制造挑战赛，全国大学生节能减排社会实践与科技竞赛，全国大学生机器人设计大赛，全国大学生电子设计竞赛，全国大学生机械设计大赛，全国大学生智能汽车竞赛}（i=1，2…，10）。

1.3.2 构建比较矩阵

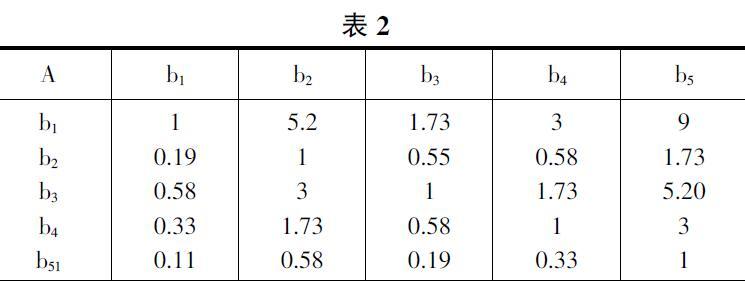
对某一竞赛，确定其准则层的评价指标集B={参赛人数b1，资金投入b2，竞赛天数b3，获奖比率b4，专家组人数b5}。对于同一竞赛，按照三度标准，构造准则层比较矩阵A=（bij）：

■

根据指标的相对重要程度和贡献不同，对竞赛指标做出排列：竞赛人数>竞赛天数>获奖比率>资金投入>专家组人数，从而构建如下的准则层和方案层比较矩阵，相对于目标层，建立准则层比较矩阵表A。相对于准则层，利用规则建立方案层比较矩阵表B1，B2（以参赛人数b1和资金投入b2为例，其它评价指标构建方法相同，后面利用极差化法处理）