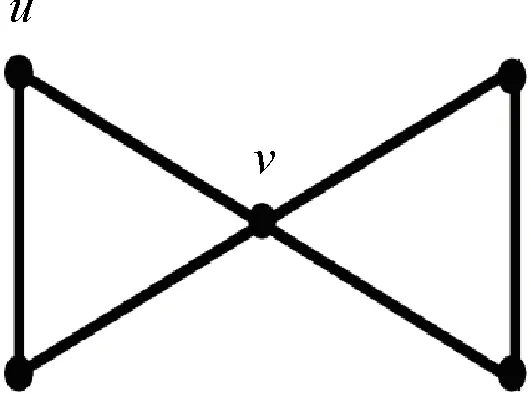
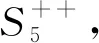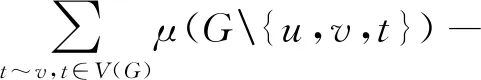一类双圈图匹配多项式的最大根
马海成, 李丹阳
(青海民族大学 数学学院, 青海 西宁 810007)
0 引 言
本文仅考虑有限无向的简单图. 设G是有n个点的图,G的一个匹配是指G的 一个生成子图,它的每个连通分支或是孤立点或是孤立边. 恰有k条边的匹配称为k-匹配. 在文献[1]中图G的匹配多项式定义为
这里p(G,k)是G中的k-匹配的数目. 为了方便, 本文将μ(G,x)简记为μ(G).
匹配多项式在数学、统计物理和化学中都有很重要的应用. 在统计物理上,它是描述一种物理系统的数学模型,首先由物理学家Heilmann等[2]为研究这种物理系统引进图的匹配多项式. 在理论化学中,匹配多项式根的绝对值的和称为该图的匹配能量,它与这个图所表示的芳香烃的活性有关[3]. 它的所有系数绝对值的和(即所有匹配的总数)就是这个图表示的碳氢化合物的Hosoya指标,它与这个化合物的沸点有关[4].匹配多项式是一种组合计数多项式,它与图的特征多项式、色多项式和其他多项式有许多联系[5-7]. 对于无圈图,它等于特征多项式;对于一般图,它是该图路树的特征多项式的一个因式[8-9]. 它有许多优美性质, 如它的根都是实数, 且关于坐标原点对称[1];它的某种形式的积分可以计算满足某些不等式条件的置换个数[1]; 它的另一种形式的积分可以计算该图的匹配能量[3]. 目前,对于匹配多项式的研究有很多[1-13],但对于匹配根取值范围的研究还很少见,本文研究了包含一个∞-图为其导出子图的一类双圈图匹配最大根的取值范围.
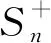
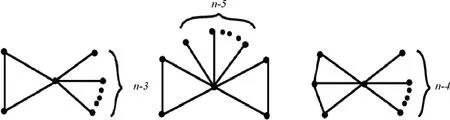
图1 图和
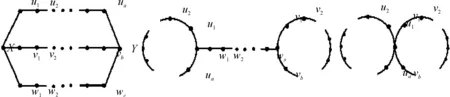
图2 图θ(a,b,c)、∞(a,s,b)和∞(a,b)Fig.2 The graphs θ(a,b,c)、∞(a,s,b) and ∞(a,b)
设G是有n个点的一个图,恰有n-1、n和n+1条边的连通图分别称为树、单圈图和双圈图. 众所周知, 双圈图有两类,包含导出子图θ(a,s,t)的双圈图的集合记为Β1,若G∈Β1, 称G是第一类双圈图. 包含导出子图∞(a,s,b)或∞(a,b)的双圈图的集合记为Β2, 若G∈Β2, 称G是第二类双圈图. 以M1(G)表示图G的匹配多项式μ(G,x)的最大根,简称为匹配最大根.本文研究了第二类双圈图的匹配最大根的取值范围,主要结论是下面的定理.
定理设G是有n个点的第二类连通双圈图,G∈Β2,则

(2)当n=5,M1(∞(2,2))≤M1(G), 仅当G≅θ(2,2)时取等号.
(3)当n≥6,M1(∞(2,n-6,2))≤M1(G),仅当两个图同构时取等号.
1 若干引理
引理1[1]设图G有k个连通分支G1,G2,…,Gk, 则
μ(G,x)=μ(G1,x)μ(G2,x)…μ(Gk,x).
引理2[1]设G是一个图,u∈V(G),e=uv∈E(G), 则
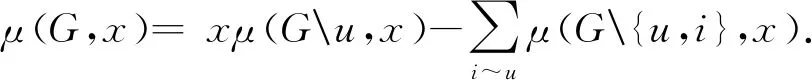
(2)μ(G,x)=μ(Ge,x)-μ(G{u,v},x).
引理3设G是一个图,u∈V(G),e=uv∈E(G), 则
(1)匹配多项式μ(G,x)的根都是实数.
(2)M1(G)≥M1(Gu), 若G连通,则M1(G)>M1(Gu).
(3)M1(G)≥M1(Ge), 若G连通,则M1(G)>M1(Ge).
证明(1)、(2)见文献[1].
(3)由于μ(G,x)=μ(Ge,x)-μ(G{u,v},x),而μ(G,x)的最大根大于等于μ(G{u,v},x)的最大根,这说明,当x≥M1(G)时,μ(G{u,v},x)≥0. 引理2(2)也隐含着μ(G,x)的最大根大于等于μ(Ge,x)的最大根. 若G连通,μ(G,x)的最大根大于μ(G{u,v},x)的最大根,这说明,当x≥M1(G)时,μ(G{u,v},x)>0.这也隐含着μ(G,x)的最大根大于μ(Ge,x)的最大根.
□
引理4[14]设P(s,t)=Ps∪Pt,k≤s≤t是整数,则
μ(P(s,t))-μ(P(s-k,t+k))=
μ(P(k-1,t-s+k-1)).
约定μ(P0)=1,μ(P-1)=0,引理4对k≥0的整数都是对的.

设G是一个连通图,e=uv∈E(G),且u和v在图G中没有公共邻点,即N(u)∩N(v)=φ. 构造一个图G(e)如下:先从图G中删除边e, 然后黏结点u和v成为一个点w, 最后在点w依附一个悬挂点z,见图3. 记e′=wz. 明显的,当e是G的一条悬挂边时,G≅G(e). 将图G变为G(e)的图变换称为第一种图变换.
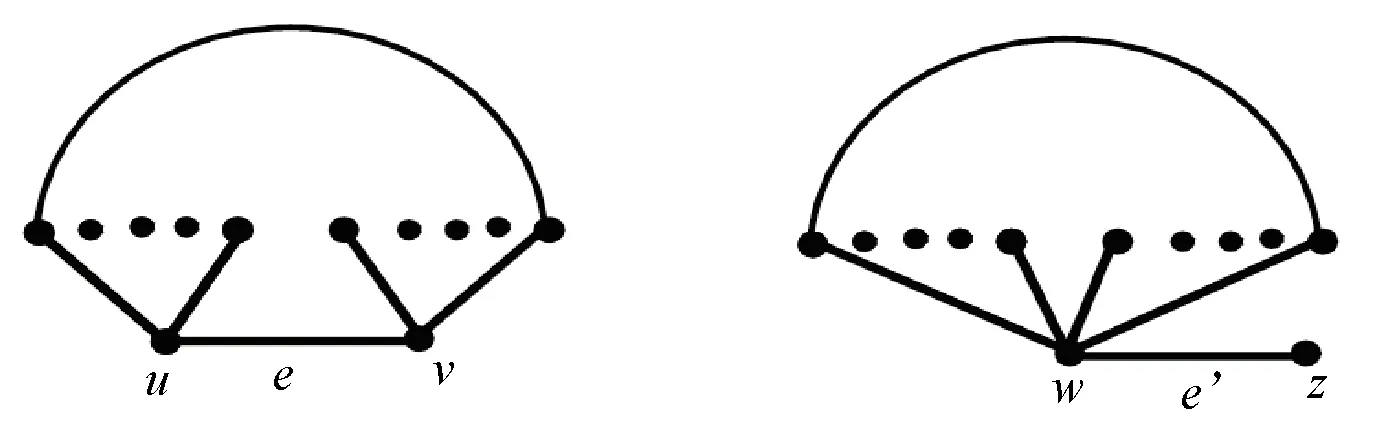
图3 图G和G(e)Fig.3 The graphs G and G(e)
引理5设d(u)≥2,d(v)≥2,N(u)∩N(v)=φ, 则
μ(G)-μ(G(e))=
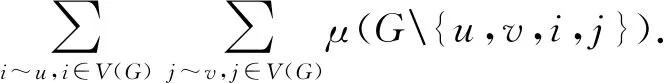
证明由引理2(1),
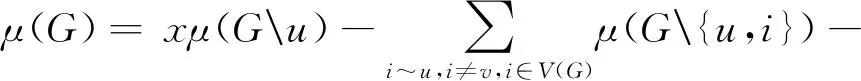
μ(G{u,v})=
x[xμ(G{u,v})-
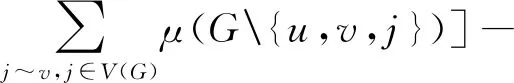

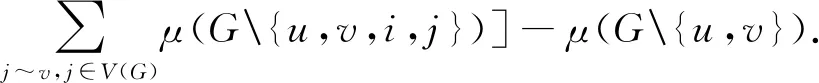
μ(G(e))=xμ(G(e)w)-
由图G(e)的构造知,
x2μ(G{u,v})=xμ(G(e)w),
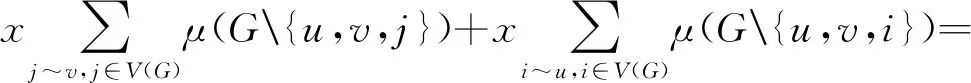
且
μ(G{u,v})=μ(G(e){w,z}),
μ(G)-μ(G(e))=
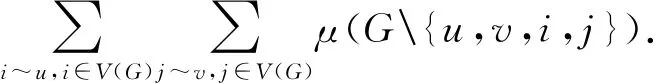
□
设G是至少有两个点的连通图,u∈V(G), 路Pn的点从一端到另一端分别标记为v1,v2,…,vn,图G的点u和路Pn的点vi黏结后得到的图记为Gu,iPn(图4). 将图Gu,iPn变为Gu,1Pn的图变换叫第二种图变换.
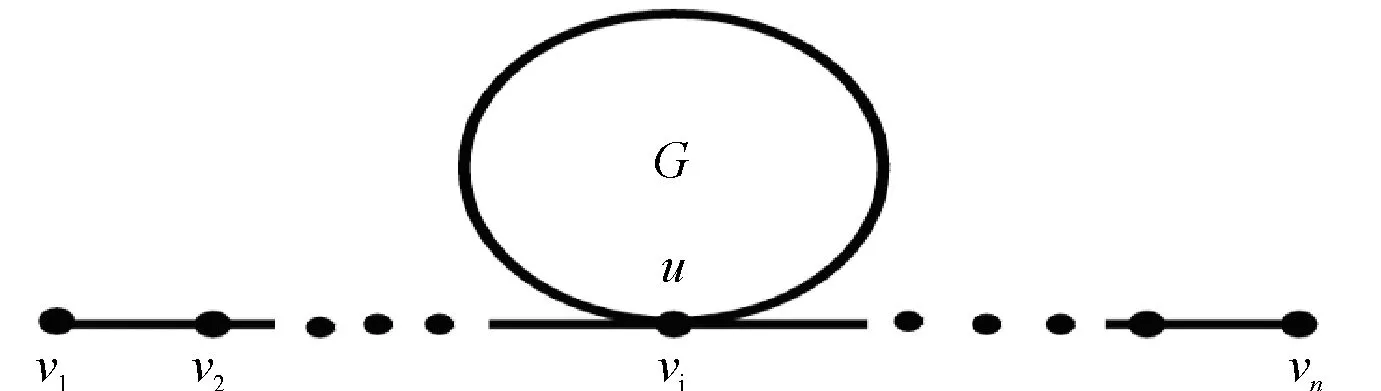
图4 图Gu,iPnFig.4 The graph Gu,iPn
引理6设G是至少有两个点的连通图,u∈V(G),n≥3,1 μ(Gu,1Pn)-μ(Gu,iPn)= 证明与引理5的证明类似,略. □ 图5 图和 引理7设G、H1和H2是三个连通图,u,v∈V(G),u′∈V(H1),u″∈V(H2), 则 证明与引理5的证明类似,略. □ 在图G的自同构群下属于同一轨道上的点称为相似点, 点u和v在图G中相似当且仅当存在G的一个自同构π, 使得π(u)=v. 推论设G、H1和H2是三个连通图,u,v∈V(G),u′∈V(H1),u″∈V(H2), 且点u和v在图G中相似, 则 证明由点u和v在图G中相似,可以得到 由引理7得证. □ 设G是一个图,e=uv∈E(G), 在边e中依次插入n个点v1,v2,…,vn后得到的图记为Ge,n(图6). 图Gu,1Pn+1的记号同引理6. 将图Gu,1Pn+1变为Ge,n的图变换叫第四种图变换. 图6 图Gv,1Pn+1和Ge,nFig.6 The graphs Gv,1Pn+1 and Ge,n 引理8设G是一个连通,e=uv∈E(G), 则 μ(Ge,n)-μ(Gv,1Pn+1)= 证明与引理5的证明类似,略. □ 引理9设G1,G2是两个n阶连通图,如果存在图G1的真子图Hi(i=1,2,…,s), 满足 则 M1(G1) 证明由引理3知,μ(G)的最大根大于μ(Hi)的最大根,说明当x≥M1(G)时, 这也隐含着μ(G2)的最大根大于μ(G1)的最大根. □ 设G是一个连通图,u∈V(G)、(T,v)是带有根点v的一棵n(≥2)阶树, 以Gu,vT表示将图G的点u和T的点v黏结后得到的图,K1,n-1为n个点的星图, 中心点记为w. 引理10设G是一个连通图,u∈V(G),(T,v)是带有根点v的一棵n(≥2)阶树, 则 M1(Gu,vT)≤M1(Gu,wK1,n-1), 仅当Gu,vT≅Gu,wK1,n-1时取等号. 证明对图Gu,vT的G与T之间的割边重复地使用第一种图变换和引理9,得证. □ 引理11设G是一个连通图,u∈V(G),(T,v)是带有根点v的一棵n(≥2)阶树, 则 M1(Gu,1Pn)≤M1(Gu,vT), 仅当Gu,vT≅Gu,1Pn时取等号. 证明对图Gu,vT的树T上的距离点v最远的分叉点(度数大于2的点)重复地使用第二种图变换和引理9,得证. □ 注意在图∞(a,s,b)中, 两边的参数a和b分别表示两个圈上的点数是a+1和b+1, 中间的参数s表示两个圈之间的轴上的点数(不包括圈上的点), 下面的引理给出在一定条件下, 将圈上的点移动到轴上后的匹配多项式之间的关系. 引理12 设3≤a,0≤s, 2≤b, 且a≤b+s+3, 则 μ(∞(a,s,b))-μ(∞(a-1,s+1,b))= 证明由引理2(2)知, μ(∞(a,s,b))=μ(Q(b,s+a+1))- μ(Q(b,s)∪Pa-1), μ(∞(a-1,s+1,b))=μ(Q(b,s+a+1)- μ(Q(b,s+1)∪Pa-2),则 μ(∞(a,s,b))-μ(∞(a-1,s+1,b))= μ(Q(b,s+1)∪Pa-2)-μ(Q(b,s)∪Pa-1)= [μ(Pb+s+2)-μ(P(b-1,s+1))]μ(Pa-2)- [μ(Pb+s+1)-μ(P(b-1,s))]μ(Pa-1)= [μ(P(b+s+2,a-2))-μ(P(b+s+1,a-1))]- μ(Pb-1)[μ(P(s+1,a-2))-μ(P(s,a-1))]. (1)当a≤s+1, 即s≥a-1, 此时必有b+s+1≥a-1,由引理4知 μ(∞(a,s,b))-μ(∞(a-1,s+1,b))= -μ(Pb+s-a+2)+μ(P(b-1,s-a+1))= -μ(Q(b,s-a+1)). (2)当a=s+2, 即s+1=a-1, 此时必有b+s+1≥a-1,由引理4知 μ(∞(a,s,b))-μ(∞(a-1,s+1,b))= -μ(Pb+s-a+2). (3)当s+3≤a≤b+s+2, 即a-2≥s+1且b+s+1≥a-1,由引理4知 μ(∞(a,s,b))-μ(∞(a-1,s+1,b))= -μ(Pb+s-a+2)-μ(P(b-1,a-s-3)). (4)当a=b+s+3, 此时必有a-2≥s+1, 由引理4知 μ(∞(a,s,b))-μ(∞(a-1,s+1,b))= -μ(P(b-1,a-s-3)). 引理13设2≤a,0≤s,2≤b, 且b+s+4≤a, 则 μ(∞(a,s,b))-μ(∞(s+2,a-2,b))= -2μ(P(a-s-3,b-1)). 证明由引理2(2)知, μ(∞(a,s,b))=μ(Q(b,s+a+1))- μ(Q(b,s)∪Pa-1), μ(∞(s+2,a-2,b))=μ(Q(b,s+a+1)- μ(Q(b,a-2)∪Ps+1),则 μ(∞(a,s,b))-μ(∞(s+2,a-2,b))= μ(Q(b,a-2)∪Ps+1)-μ(Q(b,s)∪Pa-1)= [μ(Pb+a-1)-μ(P(b-1,a-2))]μ(Ps+1)- [μ(Pb+s+1)-μ(P(b-1,s))]μ(Pa-1)= [μ(P(s+1,b+a-1))-μ(P(a-1,b+s+1))]- μ(Pb-1)[μ(P(s+1,a-2))-μ(P(s,a-1))]= -μ(P(a-s-3,b-1))- μ(P(a-s-3,b-1))= -2μ(P(a-s-3,b-1)). □ 引理14 设3≤a,2≤b, 则 μ(∞(a,b))-μ(∞(2,a-3,b))= -μ(P(b-2,a-3))-μ(P(1,b-1,a-3)). 证明由引理2(2)知, μ(∞(a,b))=μ(Q(b,a))-μ(P(b,a-1)), μ(∞(2,a-3,b))=μ(Q(b,a))-μ(P1∪ Q(b,a-3)),则 μ(∞(a,b))-μ(∞(2,a-3,b))= μ(P1∪Q(b,a-3))-μ(P(b,a-1))= [μ(P(1,b+a-2))-μ(P(b,a-1))]- μ(P(1,b-1,a-3))=-μ(P(b-2,a-3))- μ(P(1,b-1,a-3)). □ 图7 图 由于 此时引理7变为 由引理9, 得到定理的(1). 由引理11, 将依附于∞-的每棵树替换成同样点数的路, 其匹配最大根会减小. 再重复使用第四种图变换, 逐步将∞-上悬挂的路变为内部路, 最后变为一个n阶的图∞(a′,s′,b′)或∞(a′,b′), 由引理8, 其匹配最大根会减小. 5个点的∞图只有一种, 即∞(2,2), 因此, 定理的(2)成立. (3)n≥6,如果∞(a,s,b)不同构于∞(2,n-6,2). (i)当a≤b+s+3时, 由引理12和引理9知,M1(∞(2,s+a-2,b)) (ii)当a≥b+s+4时,由引理13和引理9知,M1(∞(s+2,a-2,b)) 不论是(i)还是(ii), 均得到M1(∞(2,s+a-2,b)) (iii)对图∞(a,b),由引理14及上面的(i)和(ii)知,M1(∞(2,n-6,2)) □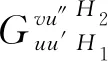
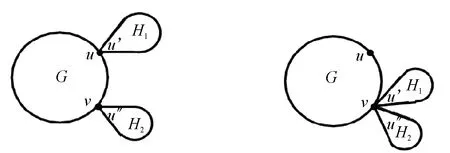
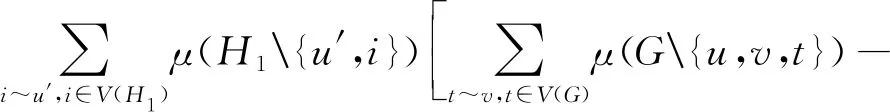
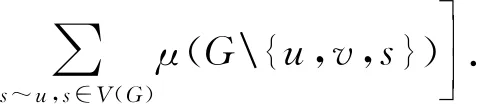
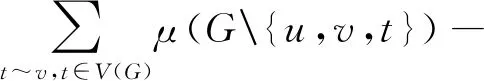

2 主要定理的证明