传感网中数据驱动的多时段控制方法优化研究

徐 琛，董德存，欧冬秀

同济大学 道路与交通工程教育部重点实验室，上海市轨道交通结构耐久与系统安全重点实验室，上海 201804

1 引言

传感网是将信息世界与物理世界融为一体的大规模具有自组织能力的感知网络，随着传感网技术的迅猛发展，交叉口周围越来越多的交通要素都可纳入传感网大数据感知体系，数据种类越来越丰富[1]。可通过对海量数据的处理与关联性精细化分析，赋予传统数据更多的属性，增加数据的维度。智慧交通控制是减小交叉口冲突、提高交通运行效率的一种有效途径。本人全程参与多个城市交通控制系统规划以及智能交通控制系统工程建设，根据目前的工程实施效果，感应控制对于易堵区域主要交叉口，特别是当交叉口高峰期间流量已经接近饱和状态时，其控制策略容易出现冲突与混乱，造成交叉口瘫痪及流量溢出甚至导致主干路或者整个区域的大面积拥堵，控制效果往往非常不理想。此时交通管理者对控制系统稳定性的追求往往远大于先进性。从控制效果和实施成本等多角度分析，多时段控制仍是大多数城市采用的最主流的控制方式。

多时段控制（Time-of-Day，TOD）是根据交叉口流量的变化把一天24 h划分为若干个时间段，针对不同的交通时段采用不同的信号控制方案，交通信号机根据预定设置的时段划分方案自动进行控制方案的切换。多时段控制对交通信息采集的依赖程度很低，并且可靠性好。

所谓常峰型交叉口其特点一般为枢纽、商圈周边等交通流集聚性强的大型交叉口，其交通流大多数时间都处于高峰附近震荡。基于高速增长的机动车保有量以及现有交叉口空间改造的种种限制，导致目前“常峰型”交叉口现象非常普遍。研究表明，与交通流高度匹配的多时段控制时段划分方案能显著提高交通通行能力，有效降低交通延误[2]。

“常峰型”交叉口多时段控制不但要关注交通流量的稳定性与有序性，更应该重点观察内部流量主方向的瞬息状态变化。所以若将交叉口高峰期间的平稳时段归为一个信号控制时段是不合理的，会产生许多不必要的由于分段点划分设计与现实交通状况严重不匹配而带来的可避免的盲目的交通延误。

综上所述，传统总流量划分方法忽略了两方面的问题。（1）单纯以交叉口总流量为主判断依据忽略更加重要的交叉口交通流内部方向转换的变化，造成分段点划分方案与交通流实际供给能力严重不匹配。（2）传统CUSUM时段划分方法虽然对交通流整体有着一定的把握，但是对于突发冲突点情况敏感性不强，亟待重构优化。

2 预备知识

根据《中国智能交通行业发展年鉴（2018）》中重点城市智能交通控制系统建设与发展内容表述，目前我国大多数城市交叉口多时段控制方案主要是人工经验划分，即交通工程技术人员根据采集的交叉口交通流量，绘制流量时间曲线图，结合曲线的控制特征人工来划分交叉口多时段控制方案。传统的多时段控制人工划分方法主要依据工程技术人员的主观判断，其划分结果具有很大的主观性和片面性，对时段划分的客观合理性存在影响，也难以满足新一代城市交通的随机性与突发性的需求。近些年，利用传感网结合大数据技术对多时段控制方法进行精细化的优化已经成为传感网与智慧交通控制结合应用研究的热点问题。国内外诸多学者为此展开了大量的卓有成效的研究工作，并取得一定丰硕成果。为解决传统人工经验划分方法的不足，文献[3]将每15 min采集一次的交叉口交通流量数据按照时间序列排序，采用交叉口交通流量分级指标的时间变量确定聚类族群数，提出消减算法结合K-means算法的方式寻找最优分段点，并且利用Synchro7仿真软件验证其有效性，但是对噪声无抗干扰能力。文献[4]以交叉口交通延误为评价指标，基于大量的交叉口交通流量历史数据通过Kohenen聚类算法与K-means算法对比分析，证明K-means算法在聚类分析中的卓越效益，但K-means算法需提前制定聚类个数以及初始聚类中心，容易导致陷入局部最优。文献[5]基于交通数据进行修补的基础上，通过混合聚类算法确定多时段控制分段点个数和相应的最佳切换时刻，利用K-means算法收敛快的优势，对历史交通流量数据进行初始聚类，以改进立方群准则作为聚类终止条件，再运用系统聚类的方法进行分析和详细聚类。为减少分段点方案频繁切换对交通状态的扰动，算法加入对交通数据时序性的考虑，并对分段点中的歧义点进行处理，具有一定效果。

单因素时段划分方法已经取得一系列的长足进步，但是仍不能满足实际需求。因而，文献[6]以交通流量与信号周期两个变量进行多因素划分应用在多个交叉口多时段协调控制。提出交通成本作为算法评价指标的重要因素。与之前的研究仅考虑分段点之间的交通成本不同，其充分考虑两个不同控制方案切换期间的过度阶段的交通成本。文献[7]提出一个先进的聚类分析方法应用在协调控制系统。此方法基于交通数据中心提供的大量实时数据，以交通流突变时间作为时段划分的主要因素，以交通延误与平均车速为评价指标，对交叉口交通流量、信号控制配时方案周期、相位差等进行时段划分多因素聚类分析，取得一定效果。文献[8]提出以交通流流量和交通流方向为主要判断依据，基于极坐标建立流量与向量的二维模型，同时结合CUSUM算法进行聚类。通过对极坐标之下向量距离的聚类分析，在总流量相似的情况下，区分各分流量的差异，提出新的时段划分方案。以苏州工业园区的107个交叉口的数据做测试与仿真，实验证明交叉口的延误和停车时间都有不同程度的改善。本文作者于文献[9]提出以交叉口交通流总流量、总流向、与下游冲突点的时间频度构建三维向量，并对相邻三维向量间距离进行递归与合并确定多时段控制方案各个分段点。以绍兴市越城区155个交叉口实际交通流量数据为测试数据，利用创新五数概括法对测试数据进行处理，将交通流的不同特征分为不同类型的交叉口，测试结果表明该方法运用在符合“驼峰型”交通流特征的交叉口时，与传统单因素总流量时段划分模型相比其控制方案能够有效降低车辆的平均延误，具有一定的工程实施效果。但是对于“常峰型”和“多峰型”交叉口，其延误反而略有上升，说明其专有性较强。

上述研究中单因素时段划分模型中仅仅单一利用一种数据是无法精准掌握交叉口交通流实际状况，而多因素时段划分方法，虽然克服了单因素提取对象单一的问题，但是过多的影响因素参与算法，不仅计算复杂，而且造成时段划分过于琐碎，严重影响控制效率。特别是随着传感网大数据理论与技术越来越成熟，构建的新模型的专有性越来越显著，其有可能只是针对于某一种特定交通特征条件下的深度应用，这种模型并不适用于大多数情况。故本文将重点研究“常峰型”交叉口的交通特性，进一步改进与优化多时段控制时段划分模型。同时将设计全新的时间序列自回归滑动平均模型对其时段划分方案进行重构与归并优化[10-18]。

3 模型构建

“常峰型”交叉口交通流三维向量时段划分模型构建：本文建立交通流三维向量时段划分模型，其中交通流三维向量包括15 min内该交叉口交通流总量、交通流的总流向、与下一个冲突点的时间长度三个要素。

目前传统主流的“常峰型”交叉口多时段控制时段划分模型是以交叉口全天交通流总流量为主要判断因素、信号配时周期以及其他因素作为辅助判断依据，同时利用聚类算法对关联度高的时段进行递归，边界点就是多时段控制分段点。本文对上述传统分段点划分模型进行深入挖掘研究，发现一些问题。以某城市交叉口交通流量数据为例进行说明。

由图1可知，实线代表交叉口总流量为四个进口方向进入该交叉口内部的流量之和；大虚线代表南北方向分流量为南进口方向流量与北进口方向流量之和；小虚线代表东西方向分流量为东进口方向流量与西进口方向流量之和；数据采集频率为每15 min采集一次，全天共96条数据。处于在序号37至73之间的交通流量总体平稳，如果按照传统交叉口总流量划分方法，此交通流量区间段应该划分为一个控制时段。然而在对其总流量下东西方向和南北方向流量进行数据分析与挖掘，会发现在此区间东西方向与南北方向发生多次剪刀式交叉产生多个交叉点，本文定义为冲突点，如图1黑色圆点表示。此冲突点的产生说明在交叉口总流量稳定的条件下，其南北方向与东西方向流量在大方向上发生交错，总流向产生根本性转变，前半段是南北方向流量较大，后半段是东西方向流量较大，内部交通流量方向转变差异性明显。

图1 某市交叉口交通总流量与分流量分布图

3.1 模型变量定义

根据交叉口交通流进出流量平衡原理，将交叉口总流量分为交叉口四个方向的进口交通流量，定义变量Xe、Xw、Xs、Xn表示交叉口东、西、南、北四个进口方向的分流量，其中Xe、Xw、Xs、Xn均为正值。数据每15 min采集一次，故单交叉口全天交通流量数据为96条，如图2所示。

图2 变量定义示意图

Ti表示第i个时间段，i=1,2,…,96。

Xni表示该时间段Ti内的北进口交通流向量。

Xsi表示该时间段Ti内的南进口交通流向量。

Xei表示该时间段Ti内的东进口交通流向量。

Xwi表示该时间段Ti内的西进口交通流向量。

3.2 交通流总量与总流向计算

由图2可知，交通流总量Hi表示该时间段Ti内四个进口方向的流量之和。

交通流总流向定义：该时间段Ti内交叉口四个进口方向交通分流量最终拟合的总向量Oi与原点右侧横坐标轴相交的交叉的角度θi。

步骤1东西向进口交通流量拟合向量Yi计算（横坐标）：该时间段Ti内东进口交通流向量Xei−西进口交通流向量Xwi，即Yi=(0,Xei-Xwi)。

步骤2南北向进口交通流量拟合向量Zi计算（纵坐标）：该时间段Ti内北进口交通流向量Xni−南进口交通流向量Xsi，即Zi=(Xni-Xsi,0)。

步骤3该时间段Ti内交叉口四个进口方向交通分流量最终拟合的总向量Oi计算。

步骤4最终拟合的总向量Oi与原点右侧横坐标轴相交的交叉的角度θi计算，如图3所示。

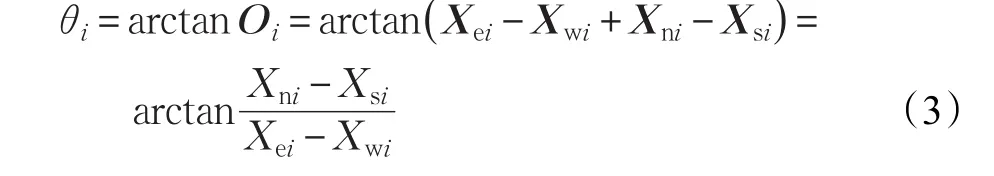
图3 交通流总流向θi定义示意图

3.3 平均时间距离计算

Tk表示第k个时间段，k=2,3,…,95。

满足公式（4）中两种条件下的一种，那么判定Tk为下游冲突点时间。同理，则定义Ti为当前时间段，Tj为当前时间段Ti前一个冲突点时间。那么当前时间段Ti与上下游冲突点的平均时间距离计算Si：

3.4 三维向量坐标体系构建

三维向量βi定义：以三维向量的形式表示在某一交叉口某一段时间内的交通总流量的大小、方向、当前时间段与上下游冲突点的平均时间距离。三维向量βi包括三个要素：（1）时间段Ti内交通总流量大小Hi；（2）时间段Ti内交通流总流向θi；（3）当前时间段与上下游冲突点的平均时间距离Si，具体表示如下：

Hi可由公式（1）计算，θi可由公式（2）、（3）得出，Si可由上述公式（4）、（5）推算归纳。

（1）相邻三维向量之间的距离计算

本文定义三维坐标下相邻三维向量之间的距离为mi。因为所有三维向量的起点都是坐标轴原点，所以计算相邻向量间距离就是计算三维空间两个向量终点间距离即可，如公式（7）所示：

公式（7）中相邻交通流三维向量之间的距离mi不仅将传统模型中的交通流量数值大小考虑在内，还将交通流总流量的方向性以及内部冲突点的分布情况也充分囊括。

4 ARMA算法实现

4.1 ARMA算法基本原理

自回归滑动平均模型（Autoregressive Moving Average model，ARMA）是研究时间序列型数据的重要方法，本文ARMA模型输入数据源为上述的相邻三维向量距离mi（其本身基于自然时间数据前后排序，非常适合ARMA预测），同时AMRA算法与CUSUM算法相比，其优势在于通过前后预测值与真实值之间的误差，可挖掘交叉口交通流冲突点的真实分布情况，对交叉口内部交通流冲突点的捕捉更为敏感。ARMA模型由自回归模型（简称AR模型）与移动平均模型（简称MA模型）为基础“混合”构成。

AR模型称为自回归模型，它的预测方式是通过过去的观测值和现在的干扰值的线性组合预测。自回归模型的数学公式如公式（8）所示：

p为自回归模型的阶数；ϕt(i=1,2,…,p)为模型的待定系数；εt为误差；为相邻三维向量距离mi经过差分平稳化后的平稳序列值。

MA模型称为滑动平均模型，它的预测方式是通过过去的干扰值和现在的干扰值的线性组合预测。滑动平均模型的数学公式如公式（9）所示：

q为模型的阶数；θj(j=1,2,…,q)为模型的待定系数；εt为误差。

ARMA模型为自回归模型和滑动平均模型的组合。其数学公式如公式（10）所示：

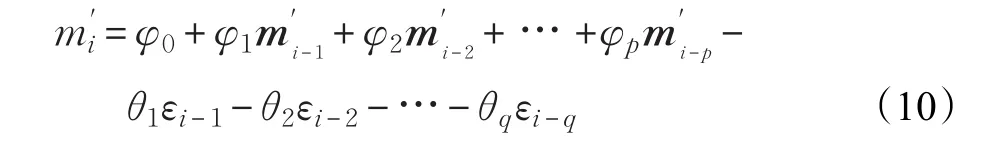
p为自回归阶数，q为移动平均阶数。φ、θ是不为零的待定系数，εi是独立的误差项。

4.2 ARMA算法流程

ARMA模型预测的逻辑框架主要包括几个方面：（1）数据处理；（2）模型识别；（3）模型定阶；（4）参数估计；（5）数据预测；（6）评价对比；（7）分段点确定，如图4所示。

步骤1对mi进行逐阶段差分（差分次数最多不超过两次），利用自相关函数和偏相关函数进行计算，判断新序列是否平稳，将数据转换成一个均值为0的平稳化序列。

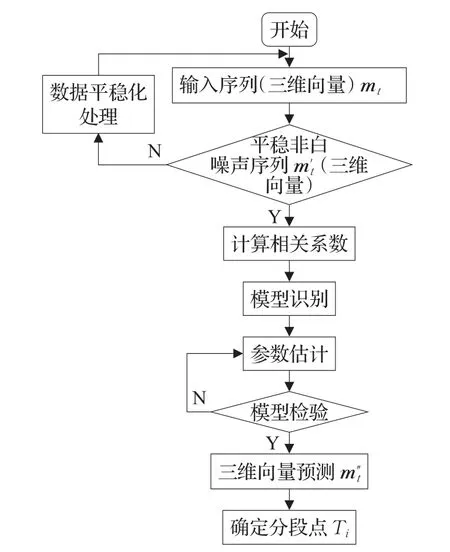
图4 ARMA算法流程图

步骤2利用AIC（Akaike Information Theoretic Criterion）最小信息准则函数对上述p和q进行定阶确定。用模型参数的估计方法计算ARMA(p,q)的模型参数和残差的方差及准侧函数值AIC(p,q)，选取AIC(p,q)最小值相应的阶数和参数为最终确定的理想模型的阶数和参数。

步骤3对步骤2中确定p和q值的ARMA(p,q)模型进行参数估计，求解公式（8）中φ和θ，使得残差平方和达到最小，得到的ARMA(p,q)的预测函数。

步骤4利用上述确定的ARMA(p,q)预测函数算出预测值，利用预测值与真实值的差值来确定时段划分的分段点。若存在时间段宽度小于等于ti=30 min，则转步骤5；否则，终止。

步骤5分析该时间段的相邻时间段的宽度，若存在时间段宽度小于等于tj=30 min，则与相邻处较短的时间段合并（若该时间段处于整个时间序列首尾边界处，则直接与相邻的时间段合并），转步骤4；否则，转步骤6。

步骤6分析该时间段交通流总流量均值和总流向均值，与相邻处时间段总流量均值和角度均值作比较，如果<σ且<μ，则将两个时间段Ti+1，Ti合并，否则转步骤5（若分割的时间段中存在时间宽度小于等于ti=30 min，则考虑合并）。

5 体系评估

5.1 测试数据分析

某城市19个交叉口；数据采集时间：2016全年366天；数据量：667 584条（96条/天/个×19个×366天）。单条数据格式：15 min内单个交叉口交通流总量（单位：pcu/h）（单个交叉口一天共96条数据）。

本文利用上述3章中的模型推算出该交叉口在三维坐标下的全天各个时间段内的交叉口交通流三维向量，并基于Matlab软件三维散点展示，如图5所示。一个数据点表示该时间段Ti内交通流三维向量的终点，起点是原点。数据点对应在X轴的数值表示该时间段Ti内交通总流量大小Hi（pcu/h）；对应Y轴的数值表示该时间段Ti内交通流总流向θi（rad）；对应Z轴的数值表示与冲突点的平均时间距离Si。每一个数据点上的序号则表示数据采集时间段Ti的先后顺序(i=1,2,…,96)。并利用公式（7）求出相邻三维向量之间的距离，如图6所示。

图5 某市交叉口全天交通流三维向量分布图

图6 某市交叉口相邻三维向量间距分布图

5.2 评估算法分析

上述相邻交叉口交通流三维向量间距借助MATLAB软件mi经过差分平稳化后处理转换成平稳序列值借助MATLAB软件利用AIC最小信息准则函数对模型参数p和q进行定阶确定。通过计算得出，p=3,q=2时AIC(p,q)值最低。确定模型阶数后，对ARMA(3,2)模型进行参数估计。通过求解，使ARMA(3,2)残差平方和达到最小，模型参数估计如公式（11）所示：

通过仿真得到结果如图7、表1、表2所示。

由图7可知，传统总流量CUSUM时段划分模型将交叉口多时段控制方案分为四个时间段，而本文创新三维向量时段划分模型分为五个时间段。以上两种方法其时间段大致分布基本上保持一致。唯一的区别就是本文创新方法将传统方法下的时序号40至序号64区间段（换算成时间为10点至16点）分为两个时间段（序号56是分段点），更加精细，不但考虑到总流量的交叉口供给匹配能力，同时也充分考虑到期间交通流方向的根本性转换。

由表1、表2对比可知，传统总流量CUSUM方法全天总延误时间为87.7 h，而本文创新时段划分方法全天总延误时间为82.4 h。本文创新时段划分方法与传统总流量CUSUM时段划分方法相比，在全天总延误时间上减少了5.3 h，下降约6.04%。特别是在临近高峰的缓冲期间10：00至16：00这一时间段，本文创新方法下总延误时间为9.75+11.4=21.15 h，而传统总流量方法为26.45 h，与传统方法相比，本文创新方法在延误时间上减少了5.3 h，相当于在此区间段延误降低约20.04%，优化效果明显。

图7 本文创新方法与传统总流量方法对比图

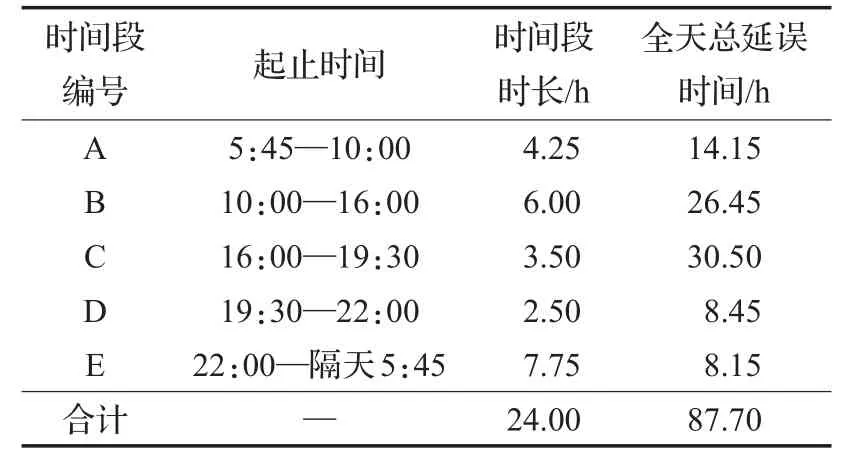
表1 某交叉口在传统总流量方法下的方案

表2 某交叉口在本文创新方法下的方案

6 结束语

常峰型交叉口特点大多数时间总体流量较大，低峰几乎不存在或者时间较短。以绍兴市平江路与人民东路交叉口为例，在这种类型交叉口中，内部冲突点几乎存在于整个平稳期内，期间发生多起冲突点跃迁现象。根据此交叉口特点利用传感网感知技术本文创新构建道路交叉口多时段控制分段点划分双阶优化模型，并对传统经典模型进行逐阶深度优化。一阶优化（模型输入数据深度优化），利用数据驱动方法赋予交通流量的方向性，增加传统交通流量数据的维度并对传统经典模型进行重构与优化。以三维向量的形式表示在某一交叉口某一段时间内的交通总流量的大小、方向以及内部冲突点分布情况。二阶优化（算法设计深度优化）运用ARMA自回归滑动平均算法对相邻三维向量间距离进行递归与合并确定多时段控制方案各个分段点。最后以某城市19个常峰型交叉口实际交通流量数据为测试数据，基于Synchro7仿真软件以本文创新时段划分模型与传统总流量CUSUM时段划分模型进行评价对比分析。结果表明，基于传感网感知技术本文创新时段划分模型运用在符合“常峰型”交通流特征的交叉口时，与传统单因素总流量时段划分模型相比其控制方案能够有效降低车辆的平均延误，具有一定的工程实施效果。