电驱移动机器人多变量固定时间连续编队控制

李艳东，朱 玲，郭 媛，于 颖，赵丽娜

1.齐齐哈尔大学 计算机与控制工程学院，黑龙江 齐齐哈尔 161006

2.齐齐哈尔大学 机电工程学院，黑龙江 齐齐哈尔 161006

1 引言

由于保持编队的一组移动机器人在很多领域的有用性，世界上很多研究者关注这一领域，并提出了多种不同的编队控制策略，如基于行为的控制[1]、虚拟结构法[2]及领航者-跟随者法[3-4]等，其中领航者-跟随者法是最常用的机器人编队控制方法。传统的编队控制[5-7]通过设计一个运动学控制器来保持编队，需满足“完美的速度跟踪”假设，其缺乏对扰动等不确定性的鲁棒性。为克服不确定性的影响，就必须考虑机器人的动力学，文献[8-10]已经包含了跟随机器人的动力学模型，以驱动器力矩作为控制输入，但实际应用中，机器人以直流电机作为驱动器，以驱动器电压作为输入更合理[11]，因此本文编队控制的研究将考虑含驱动器动力学的模型作为研究对象。

在一些实际应用中，比如军事、灾后救援、运载等领域，要求一组机器人在一定时间内达成期望的编队，而文献[12-13]等设计的有限时间控制器收敛速度受初始条件限制，初始条件变化将直接影响控制器镇定时间，无法实现这一愿望。Polyakov[14]开创的固定时间问题的研究，为解决这一问题带来了希望，释放了初始条件，通过控制器常数参数的人为设计就能决定机器人编队的达成时间，这就涉及到了固定时间编队控制问题。文献[15-17]将针对一阶、二阶标量系统的固定时间设计框架用到了多智能体系统一致控制上，然而，这些文献都是采用将多变量系统解耦成包含单输入通道的控制问题，然后再通过标量系统的固定时间设计框架进行设计，直到现在针对多变量多输入系统的固定时间控制问题进行设计的文献也不多见[18]；此外，针对非完整移动机器人，并考虑以驱动器电压作为控制输入且克服外部干扰的情况，因变量之间的耦合，增加了设计的困难性，采用多变量固定时间设计框架进行编队控制设计将更有意义。

针对多变量系统抗干扰固定时间控制设计可以采用开关控制，但因为输入的频繁动作，存在抖振现象，不利于系统实际应用，文献[19-20]提出的多变量连续类超螺旋固定时间算法很好地解决了开关控制输入抖振的问题，受此启发，本文将采用连续类超螺旋固定时间算法用到受外部干扰的移动机器人编队控制中。综合上面的分析，本文将研究一队受外部干扰作用的电驱动非完整移动机器人的多变量固定时间连续编队控制问题。

2 原理

2.1 非完整移动机器人模型

电驱动非完整移动机器人的数学模型如下[11]：

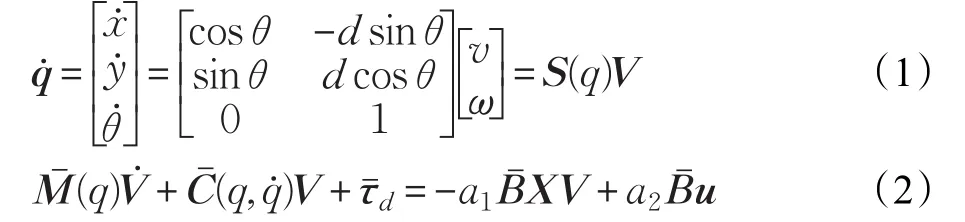
其中q=(x,y,θ)T为机器人的姿态向量，(x,y)表示后轴中点c在笛卡尔坐标系中的坐标，θ为机器人的导向角。两驱动轮的间距为2R，驱动轮的半径为r。v和ω分别为移动机器人的线速度和角速度，Mˉ(q)为系统惯性矩阵，是与位置和速度有关的向心力和哥氏力矩阵，是仅与轮距R和轮半径r有关的非奇异矩阵，为外部扰动，，ur与ul是加在右轮和左轮电机的输入电压，d是机器人后轴到前部的距离。其中矩阵：

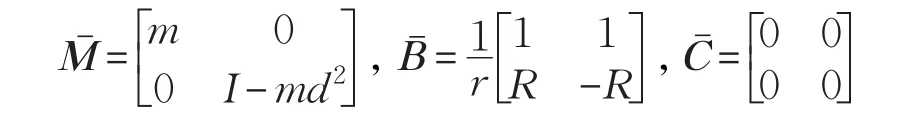
其中，m是移动机器人平台质量，I为机器人平台绕轮轴的转动惯量，为速度与左右驱动轮速度的关系矩阵，a1=N2KTKb/Ra与a2=NKT/Ra为参数；N为电机齿轮与机器人驱动轮上齿轮的齿轮比，KT为电机转矩常数，Ra为电阻，Kb是反电动势系数。

2.2 领航者跟随者编队动力学模型

考虑如图1所示相对距离为lij，相对方位角为ψij的两个受非完整约束的领航者-跟随者机器人系统。

图1 领航者-跟随者机器人系统

由图1可以得到：

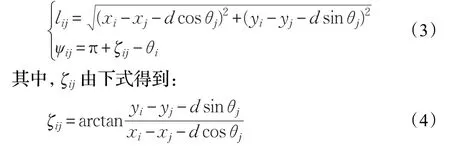
则编队系统的运动学如下[21]：

其中，γj=ψij+θij，θij=θi-θj。

注1如无特殊说明，下标i代表领航者参数，下标j代表跟随者参数，本文中j取1，2，即两台跟随者。

由式（2）、（5）可以得到考虑驱动器动力学的领航者跟随者编队状态空间动力学方程如下：

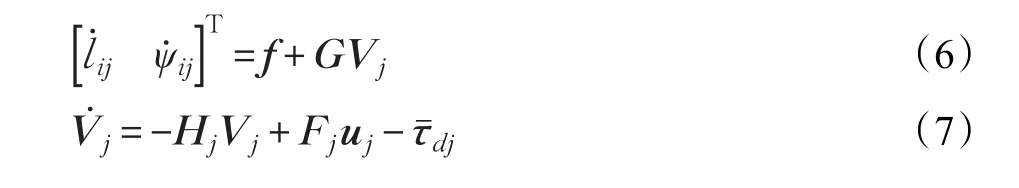
2.3 固定时间控制

在编队控制器设计之前，先介绍几个需要用到的引理和定义。

定义1[17-18]对于系统：

定义2[17-18]如果系统（8）是全局有限时间稳定，而且设定时间函数T(x0)是有界的，即>0，T(x0)≤Tmax，那么系统（8）在原点固定时间稳定。

引理1[18]如果存在一个Lyapunov函数，且对于参数α,β>0，p>1>q>0，其解满足不等式：

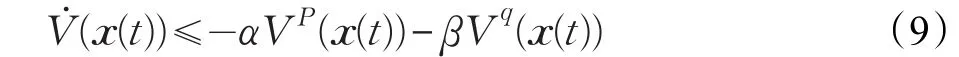
那么原点是固定时间稳定的，其设定时间函数有可以由设定常数计算出的界，即：

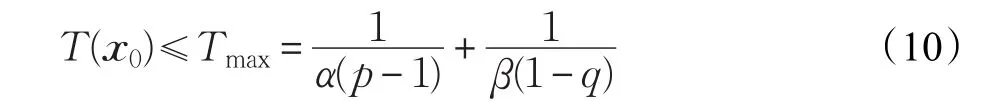
引理2[18]对于一个一阶多变量系统：

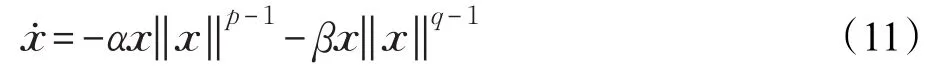
其中，x∈ℝn，α,β>0，p>1>q>0，那么，系统（11）在原点是全局固定时间稳定的，且设定时间估计由式（10）给出。

3 控制器设计

控制器设计分两部分，第一部分进行编队跟踪部分的设计，采用固定时间编队控制算法，使跟随者在不依赖初始条件的情况下，通过设计参数的选择在固定时间内达到指定的编队队形；第二部分针对跟随者机器人所受有界不确定干扰情况，依据机器人电驱动动力学模型进行抗干扰的固定时间动力学电压控制器设计。

3.1 固定时间编队控制问题

电驱动非完整移动机器人领航者-跟随者法固定时间控制的目标就是通过设计编队控制器、动力学电压控制器使：

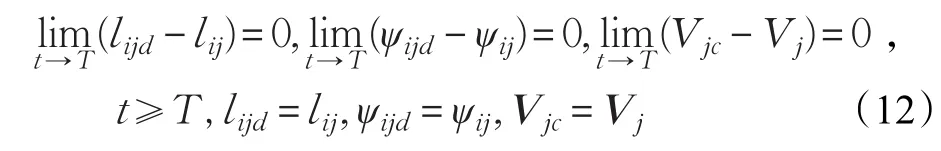
其中，lijd与ψijd分别为跟随机器人与领航机器人的相隔距离与相对方位角的期望值，Vjc为跟随者机器人的期望速度。本文主要关注跟随者机器人，给出如下假设。

假设1作用在跟随者机器人上的扰动有界，即≤ρj，ρj为正常数，其导数存在且有界，即L，L为正常数。

假设2领航者机器人跟踪一个提前定义的时变轨迹。

假设3跟随者机器人可以获得所有自身的状态和领航者机器人的速度。

3.2 固定时间运动学领航者-跟随者编队控制器

对于编队运动学系统（6），控制输入Vj=[vjωj]T，既然detG=d/lij≠0，G-1存在，假定期望的距离lijd和方位角ψijd是时不变的，使用状态反馈技术可以得到多变量固定时间运动学编队控制器（MFTFC）如下：

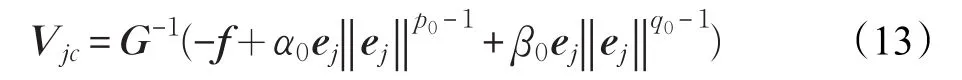
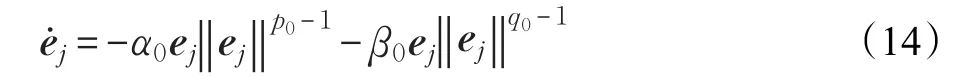
定理1对于多变量一阶系统（6），设计编队运动学控制器（13），那么编队跟踪偏差ej在设定时间函数T0内收敛到0，跟随者在通过控制器参数设计的设定时间T0内实现编队跟踪，时间T0与系统状态无关。

令 y0=≥0 ，有，式（17）则变为，则由引理1，式（17）在固定时间式（15）所示时间T0内收敛到原点，即系统（6）中的lij、ψij在固定时间内达到lijd、ψijd，实现指定编队，或者依据引理2，由运动学编队跟踪偏差微分方程（14）直接得到上述结论。证毕。

3.3 超螺旋固定时间动力学连续电压控制器

前面设计解决了编队运动学层面的固定时间编队控制问题，以设计速度控制器作为输入，可以实现跟随者在固定时间与领航者达到指定编队，但实际使用中，跟随者机器人必然受到外部干扰的影响，因此，在干扰存在的情况下，应考虑机器人动力学模型，这里，将编队控制得到的速度作为动力学（7）的期望速度输入，进行抗干扰的超螺旋固定时间动力学连续电压控制器设计，定义速度跟踪误差：

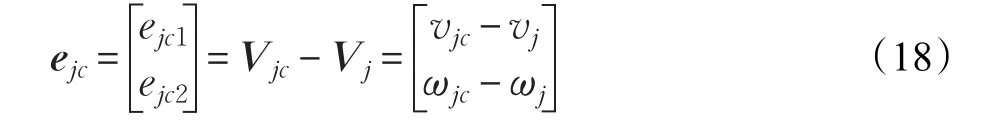
结合式（7）和（18）可以得到速度跟踪误差微分方程如下：

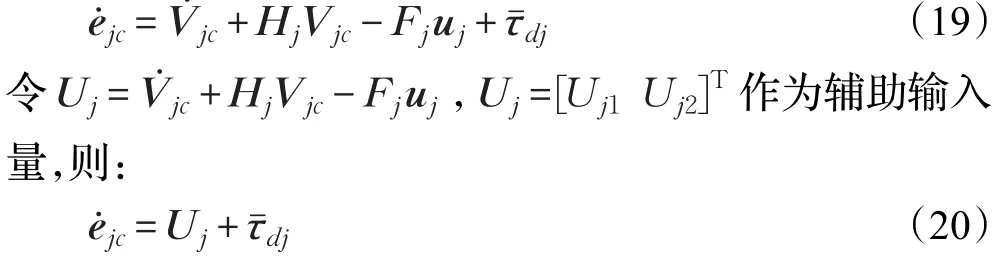
对于输入量Uj，基于文献[20]的多变量类超螺旋固定时间控制方法进行的固定时间控制器设计如下：

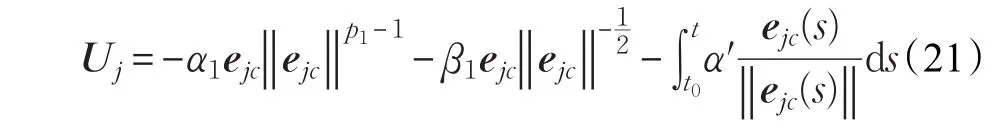
其中，p1>1，那么，闭环系统动力学有如下形式：

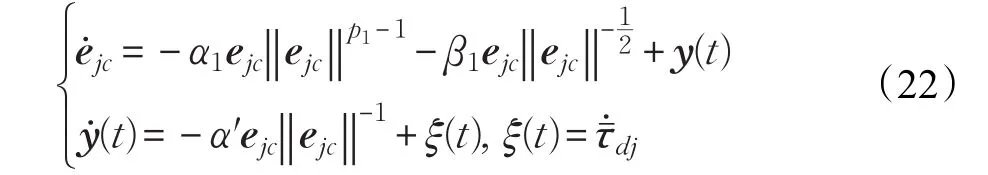
定理2对于存在干扰ξ(t)的动力学系统（22），≤L，那么，ejc和y在固定时间T1内收敛于原点，即跟随者机器人实现速度跟踪并克服外部干扰τˉdj。

定理2证明见文献[20]。

通过变量替换可以得到基于多变量超螺旋固定时间算法的跟随者机器人动力学固定时间连续电压控制器（MSTFTC）如下：

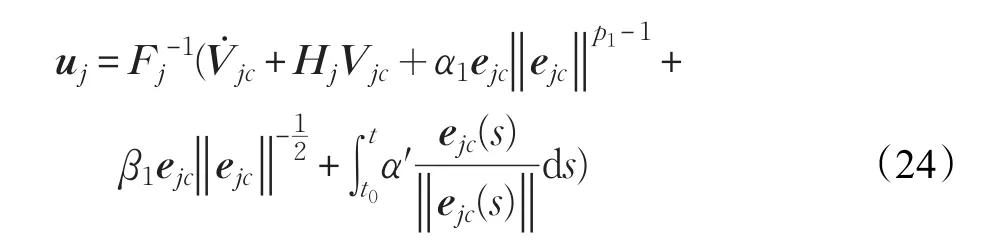
定理3对形如动力学方程（7）的电驱动跟随者机器人j，假设1～3同时满足，设计跟随者机器人驱动器电压控制器（24），那么跟随者机器人速度跟踪偏差ejc在设定时间T1（式（23））内收敛到0，跟随者在通过控制器参数设计的设定时间T1内实现动力学速度跟踪，时间T1与系统状态无关。

证明由定理2，很显然定理3成立。

为了进行对比，这里给出跟随者机器人多变量固定时间鲁棒控制器（MFTRC）如下：

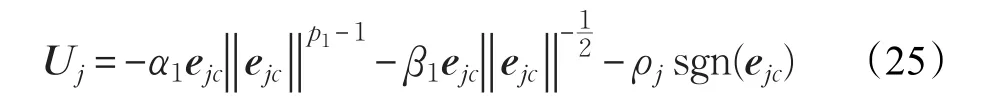
其中，α1，β1，p1为设计常数，同式（24），sgn(⋅)为符号函数，显然式（25）采用开关控制项来克服干扰，为非连续控制。

进一步，通过变量替换得到跟随者机器人多变量固定时间鲁棒电压控制器（MFTRUC）如下：

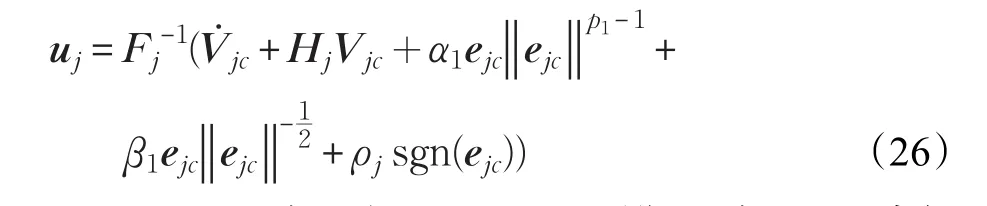
注2机器人编队在T0max内达到期望编队，跟随者在T1max内实现速度跟踪，取T=max(T0max,T1max)，则通过设计控制参数可以实现存在扰动情况下机器人编队在T内达到期望编队。

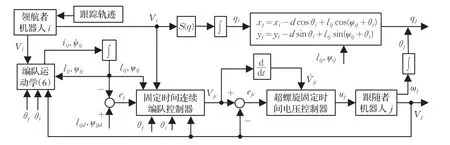
图2 电驱动移动机器人多变量固定时间连续编队控制结构图

4 仿真与结果分析

文中所设计的电驱动移动机器人多变量固定时间连续编队控制算法（MFTFC+MSTFTC）框图如图2所示，通过MATLAB/SIMULINK对所提出算法进行仿真分析，三台非完整移动机器人组成三角编队（lijd=1，ψijd=±120°）作为研究对象，取编队机器人模型物理参数完全相同如表1所示。

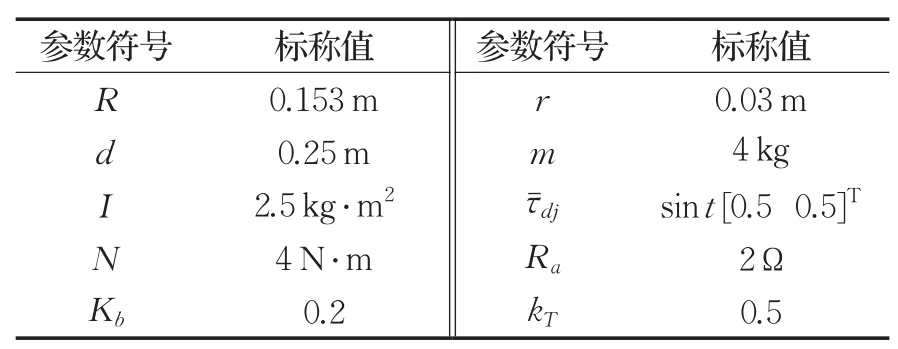
表1 机器人系统模型物理参数

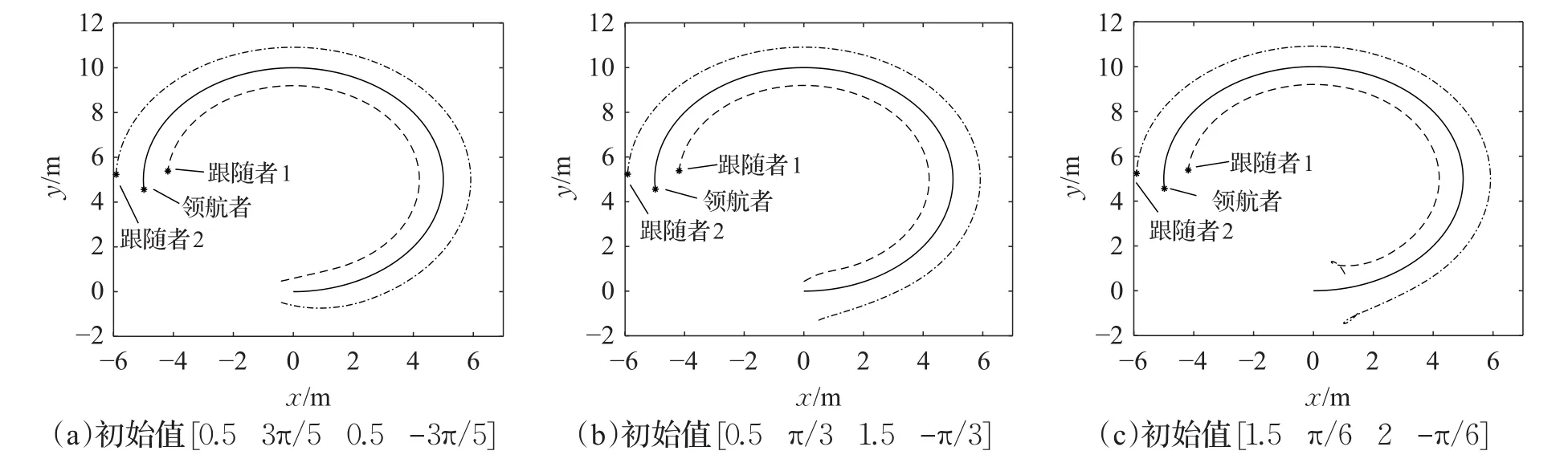
图3 三角编队圆形轨迹跟踪

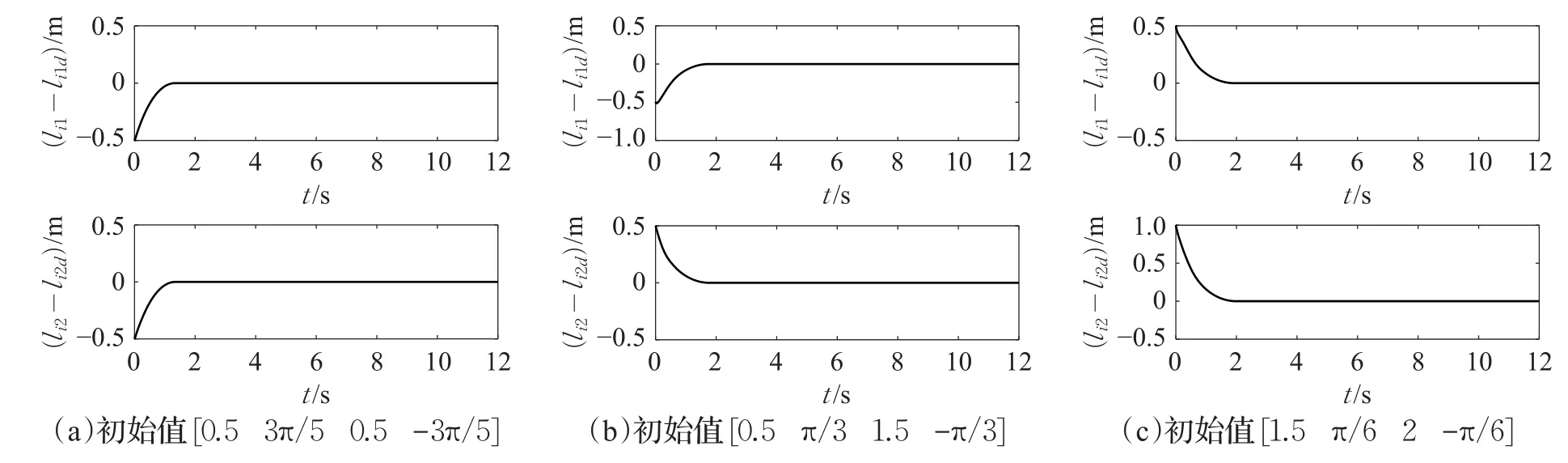
图4 跟随者与领航者相对距离跟踪偏差

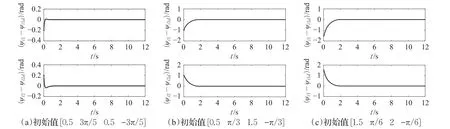
图5 跟随者与领航者方位角跟踪偏差

图6 跟随者速度跟踪偏差

图7 跟随者角速度跟踪偏差

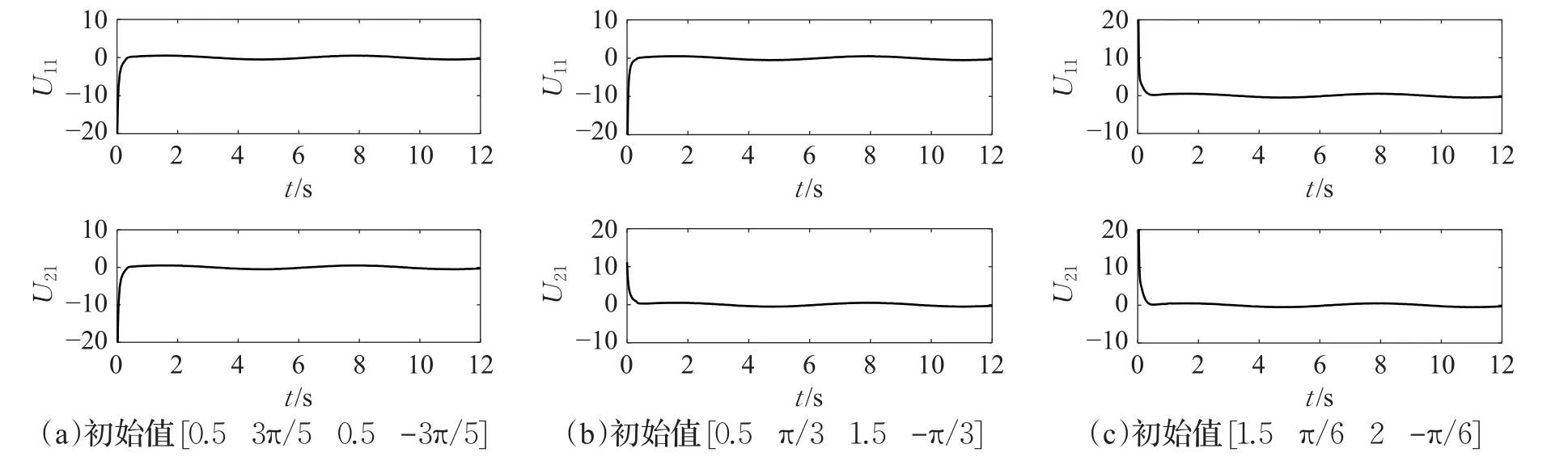
图8 跟随者输入Uj1（MFTFC+MSTFTC算法）

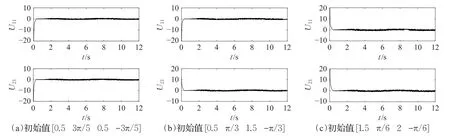
图9 跟随者辅助输入Uj1（MFTRC+MFTRUC算法）

（1）领航者与跟随者相对编队初始位姿差[0.5 3π/5 0.5-3π/5]，采用MFTFC+MSTFTC算法的仿真结果如图3～图8的（a）图所示，采用MFTRC+MFTRUC算法的仿真结果如图9（a）所示（限于篇幅，此算法只给出辅助输入Uj1用于比较研究）。

（2）领航者与跟随者相对编队初始位姿差[0.5 π/3 1.5-π/3]，采用MFTFC+MSTFTC算法的仿真结果如图3～图8的（b）图所示，采用MFTRC+MFTRUC算法的仿真结果如图9（b）所示。

（3）领航者与跟随者相对编队初始位姿差[1.5 π/6 2-π/6]，采用MFTFC+MSTFTC算法的仿真结果3～图8的（c）图所示，采用MFTRC+MFTRUC算法的仿真结果如图9（c）所示。

在参数的选取上，可以看出三种轨迹跟踪情况参数一致，领航者与跟随者相对编队初始位姿差不同，即初始条件不同，从仿真结果图3～图7（MFTFC+MSTFTC算法）中的（a）～（c）图可以看出，三种情况都实现了较好的跟踪，克服了满足假设条件干扰的影响，且几乎在相同的时间（通过控制器参数设计的设定时间）跟随者机器人达到了期望编队位置，跟随者机器人实现了对期望速度的跟踪，说明控制效果与初始条件无关，实现了固定时间控制。

在公共参数相同的情况下，三种轨迹跟踪情况，采用 MFTFC+MSTFTC 算法的图 8的（a）～（c）和采用MFTFC+MFTRUC算法的图9的（a）～（c）跟随者辅助输入Uj1的对比可以看出，连续控制的超螺旋固定时间算法（MFTFC+MSTFTC）消除了输入抖振现象，开关控制的固定时间鲁棒控制算法（MFTFC+MFTRUC）则存在明显的抖振现象，不利用实际应用。

5 结束语

文章研究了多机器人的编队控制问题，基于l-ψ领航者-跟随者控制结构提出了电驱动非完整移动机器人固定时间连续编队控制算法。依据领航者-跟随者编队动力学状态空间模型设计的多变量固定时间编队控制，以及在动力学层面，以驱动器电压作为控制量设计的多变量超螺旋固定时间连续电压控制。通过调整设计常数参数，而无需关注机器人初始状态就能够使跟随者机器人在固定时间内与领航者机器人保持期望编队，且在克服有界干扰的情况下，实现了固定时间内对理想速度的跟踪。在跟随者机器人存在干扰情况下，对三台机器人组成的三角编队以多种初始条件情况跟踪圆形轨迹进行了仿真实验，并与开关控制的鲁棒固定时间控制算法进行了对比。仿真实例及分析较好地说明了所提算法的有效性及连续控制消除输入抖振的优越性，从而增加了编队机器人在干扰存在情况下对达成编队有时间要求场合的实用性。对于机器人编队同时存在负载变化、摩擦及外部干扰等多不确定性的情况，将是进一步研究的内容。