基于穿越角度的船舶航道间隙计算方法

张 赫， 秦鲁莹， 邢江豪

(大连海事大学交通运输工程学院，大连 116026)

国际贸易的迅猛发展，航运业逐渐复苏，水路运输交通流量的快速增长，船舶航行的安全性降低，导致了诸多船舶航行的安全问题。当前船舶在穿越航道的时候，大多数采用驾驶员的主观判断与无线电相互沟通，这种方法的主观性太强，缺乏定量判断，容易引发与其他船舶的交通事故。如何在现有情况下，提高港口区域以及航道内船舶纵向穿越时的安全性变得越来越重要。

程志友等[1]以长江江苏段为例，分析了海船纵向穿越主航道时经过船舶流的避碰情形条件、操纵过程及控制要点。程志友等[2]提出交通冲突技术测量单船穿越船舶流的碰撞风险大小。李颖宏等[3]、王进展等[4]综合考虑了车辆制动过程和车辆本身尺寸对交通冲突判别的影响，建立了一种基于车型的临界冲突区域模型。Debnath等[5]提出利用交通冲突技术测量港口水域船舶碰撞危险。Ma等[6-7]提出在机器速度障碍算法基础上通过确认碰撞危险和避碰路径的方法预报客渡线水域船舶碰撞危险。程志友等[8-9]提出客渡船以合适的发船频率营运和有利的穿越间隙、穿越时机、穿越航速横越河道，能有效降低客渡船与航道船舶流的碰撞风险。

为了防控船舶横越港口以及航道时候的船舶碰撞风险，希望设计一种预测精度高、能安全穿越航道的船舶穿插间隙的计算方法，使得船舶能够以有利的穿越时机、穿越间隙、穿越角度穿越港口与航道，来有效降低船舶的碰撞风险[10]。

1 穿插模型

一种考虑船舶船体大小和角度穿越间隙计算方法，包括以下步骤。

1.1 采集航道环境资料

所述的航道交通环境资料包括航道交通环境资料和船舶大小资料以及航行速度资料。航道大致情况如图1所示。

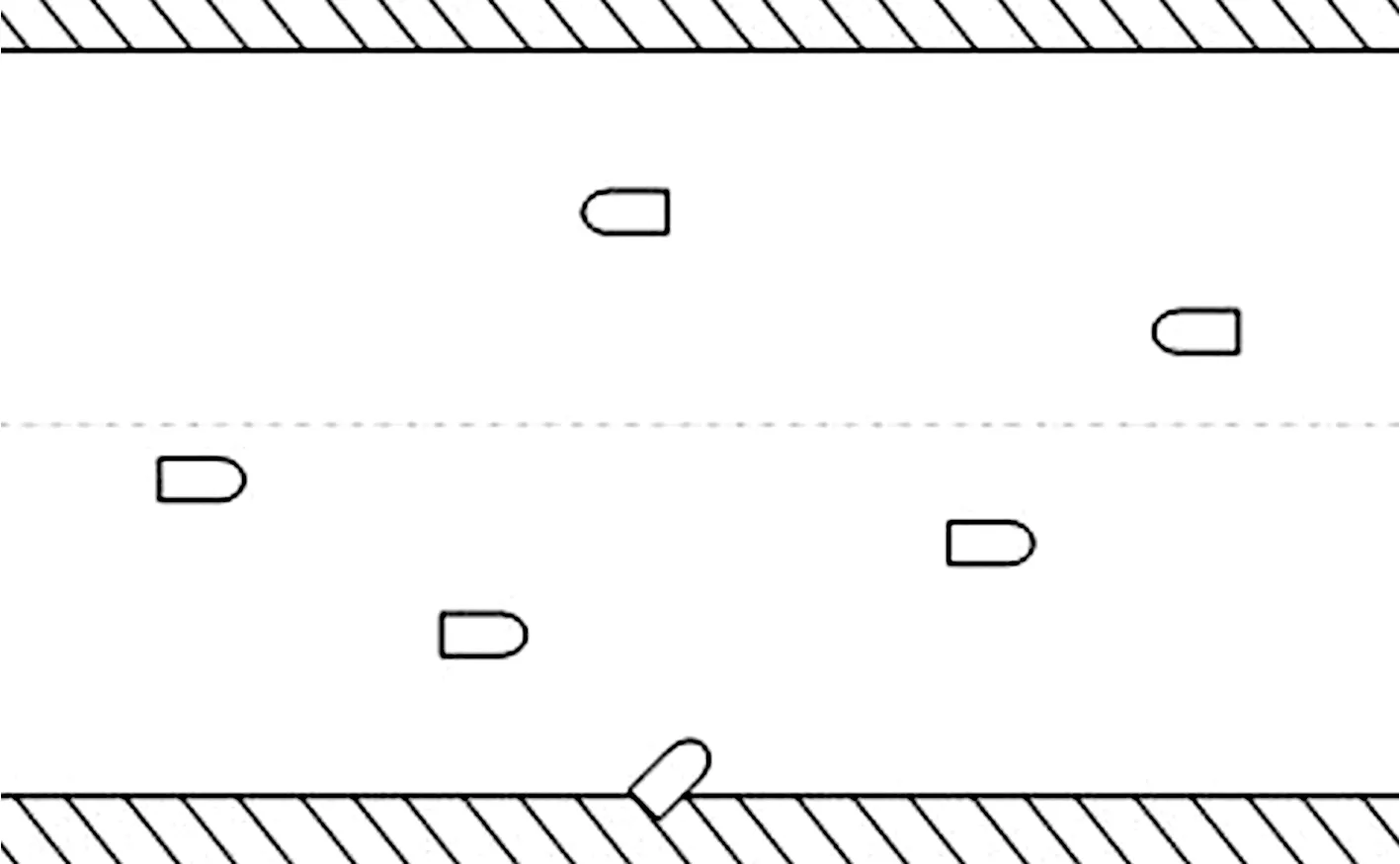
图1 航道示意图Fig.1 Waterway schematic

1.2 计算航道船舶航行时间

航道中船舶的航行方向为两个相反的方向，即上水方向和下水方向。当前定义穿越船舶处于一个准备穿越的位置时，下水方向的运输船舶为第i艘船舶，依次对下水方向的船舶进行编号；同理，上水方向的运输船舶为第j艘船舶，依次对上水方向的船舶进行编号，如图2所示。

图2 航道船舶编号示意图Fig.2 Schematic diagram of ship number in waterway

定义：vi为第i艘船的航速，方向与坐标保持一致，m/s；νj为第j艘船的航速，方向与坐标保持一致，m/s；L为航行距离；t为航行时间。则有：

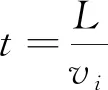
(1)

同理，对于第j艘船同样适用式(1)。

1.3 计算相关坐标位置

假设t0表示穿越船舶开始准备穿越航道的时刻，船舶o代表穿越船舶，则在t0时刻船舶i、j、o的坐标分别为i(xi,yi)、j(xj,yj)、o(xo,yo)。工程船舶准备穿越航道示意图和工程船舶准备穿越航道示意图，分别如图3和图4所示。

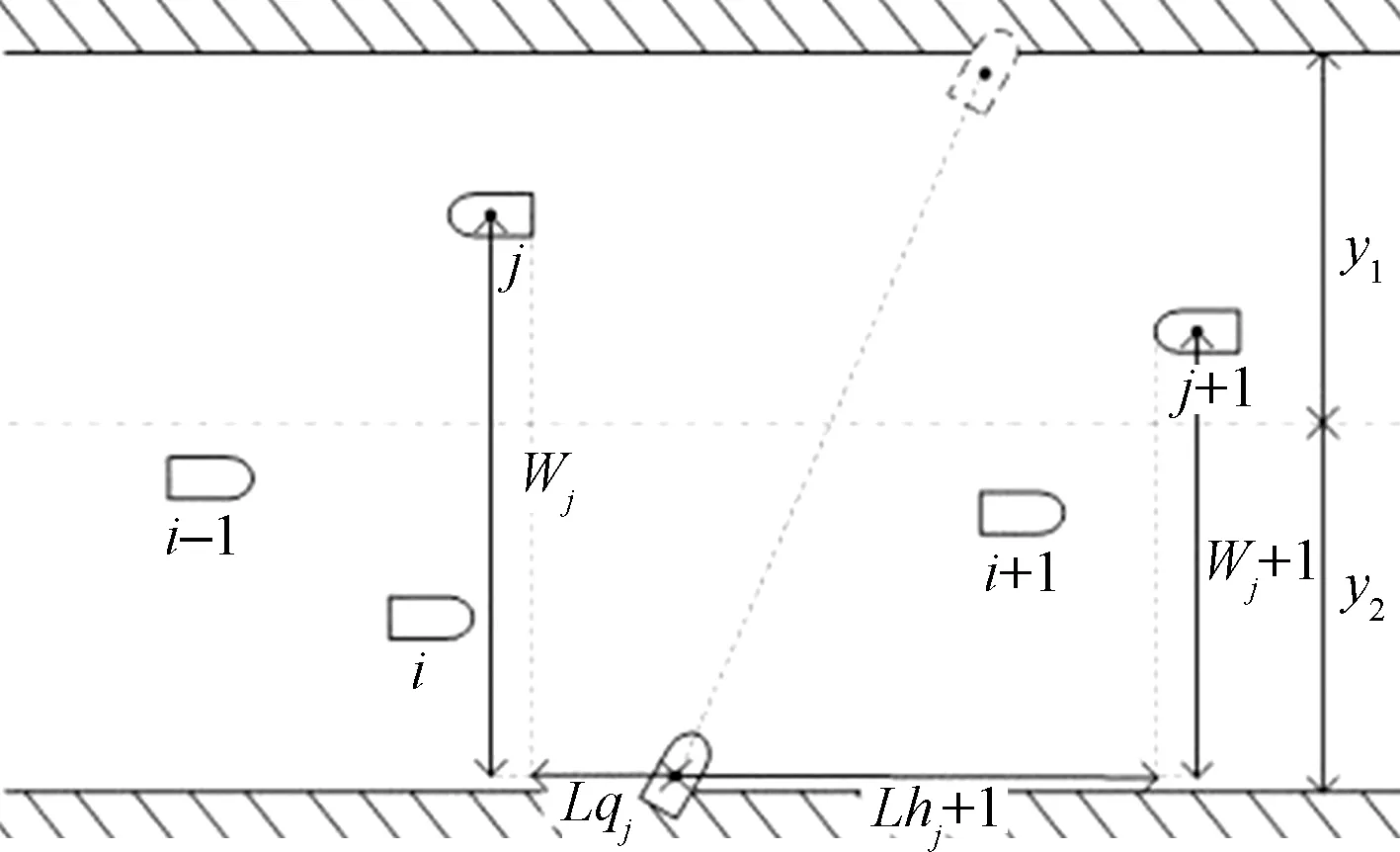
图4 工程船舶准备穿越航道示意图Fig.4 Schematic diagram of engineering ship preparing to cross the channel

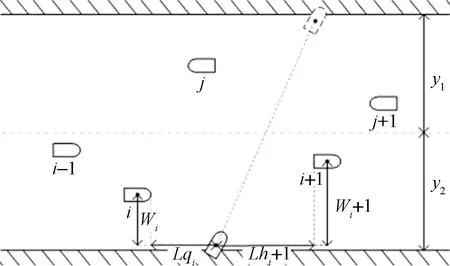
图3 工程船舶准备穿越航道示意图Fig.3 Schematic diagram of engineering ship preparing to cross the channel

定义：bi表示第i艘船的船宽，m；bo表示穿越船舶的船宽，m；bj表示第j船的船宽，m；li表示第i艘船的长度，m；lo表示穿越船舶的长度，m；lj表示第j艘船的长度，m；Wi表示穿越船舶至第i艘船之间的纵向距离，m；Wj表示穿越船舶至第j艘船之间的纵向距离，m。

则有：

Wi=yi-yo

(2)

Wj=yj-yo

(3)

1.4 计算穿越船舶以γk角度穿越时有效长度

设：vok为穿越船舶航速；γk为穿越船舶的角度。若取γk=0或π，则穿越船舶将沿着航道方向航行，即无法穿越航道，所以，γk则不可能取0或π。

穿越船舶以γk角度进行穿越，则穿越船舶是属于倾斜状态，在平行航道方向及垂直航道方向有效长度均与γk角度有关，假设：A1A3表示穿越船舶以γk角度穿越时，垂直航道方向有效长度为

A1A3=|losinγk|+|bocosγk|

(4)

A1A2表示穿越船舶以γk角度穿越时，垂直航道方向有效长度的一半：

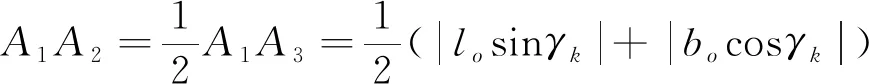
(5)

A5A7及A3A5表示穿越船舶以γk角度穿越时，平行航道方向有效长度的一半：

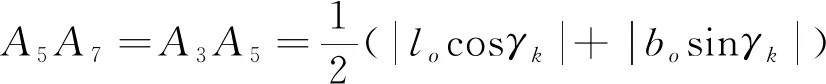
(6)

工程船以γk角度航行示意图如图5所示。

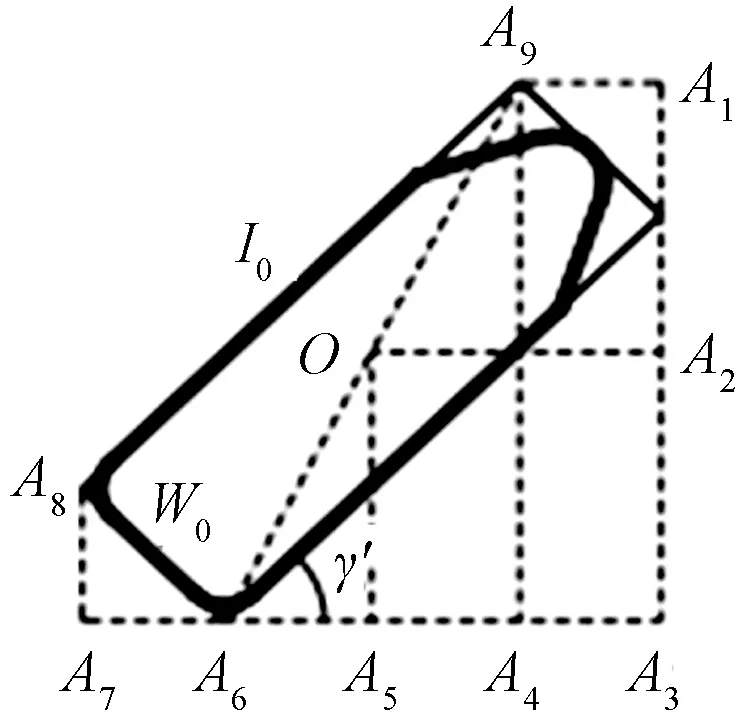
图5 工程船以γk角度航行示意图Fig.5 Engineering ship sailing at γk angles

1.5 计算穿越船舶穿越航道参数

穿越船舶在穿越航道过程中，会遇到在航道区域内航行的船舶…i-1,i,i+1…j-1,j,j+1…，在判断穿越船舶是否能安全穿越时，只要判断穿越船舶在航行过程中与其他船舶是否保持安全距离即可。若穿越船舶与其他船舶皆能保持安全距离，这说明t0时刻允许穿越，若穿越船舶与其他任意一个船舶在航行过程中小于安全距离，则说明t0时刻禁止穿越。

1.5.1 穿越船舶从第i艘船船尾穿越

如图6所示为穿越船舶从第i艘船船尾穿越。

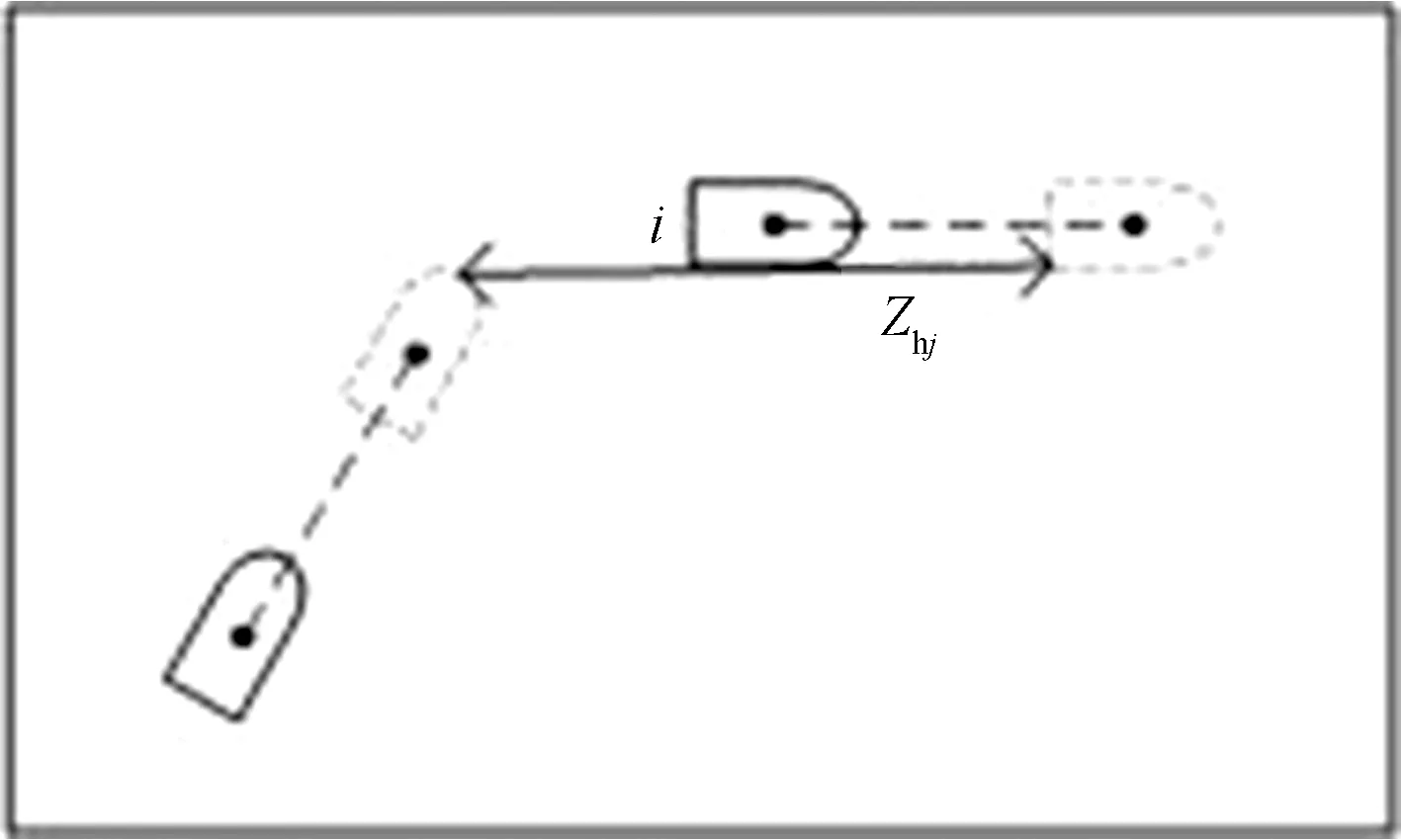
图6 穿越船舶从第i艘船船尾穿越Fig.6 Cross the ship from the stern of the i-th ship

设：thi为穿越船舶从待穿越位置航行至穿越船舶船首到达与第i艘船尾航道垂直方向的位置时，所需要的时间，s；zhi为穿越船舶航行至穿越船舶船首到达与第i艘船尾航道垂直方向的位置时，与第i艘船尾的距离，m。

由于穿越船舶在穿越过程中，使用不同航行角度，所航行距离和航行时间是不相同的，下面对航行角度进行划分，并确定各个角度范围内的航行距离和航行时间。

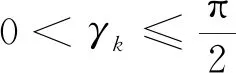
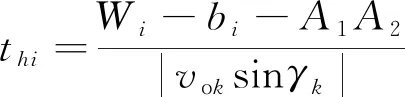
(7)

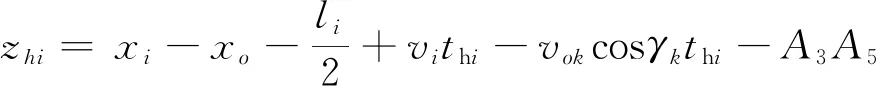
(8)

(9)

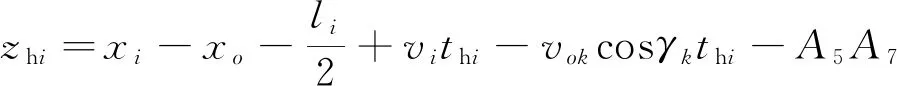
(10)

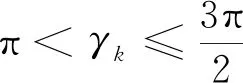
(11)

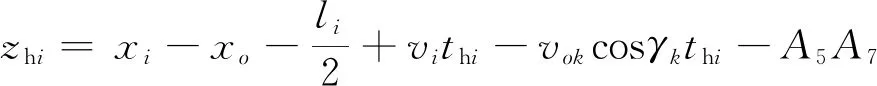
(12)

(13)

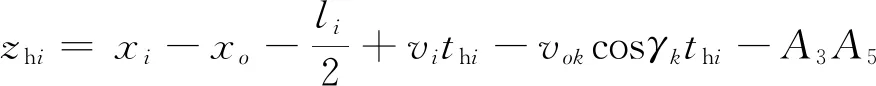
(14)

A1A2、A3A5、A5A7按式(9)、式(10)进行计算。

将上述四种情况统一如下：

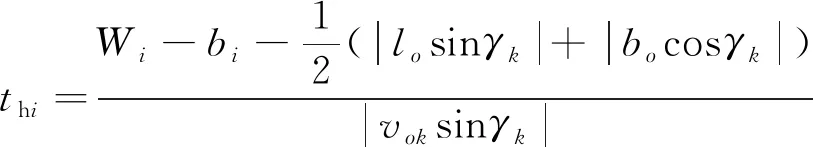
(15)

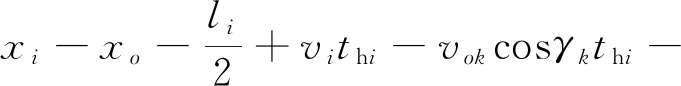
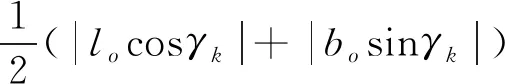
(16)

1.5.2 穿越船舶从第i艘船船首穿越

穿越船舶从第i艘船船首穿越与穿越船舶从第i艘船尾穿越类似，也为四种情况，并将其统一如下。

设：tqi为穿越船舶从待穿越位置航行至船尾刚刚离开第i艘船航道垂直方向位置时，所需要的时间，s；zqi为穿越船舶从待穿越位置航行至船尾刚刚离开第i艘船纵向位置时，与第i艘船首的距离，m。

则：

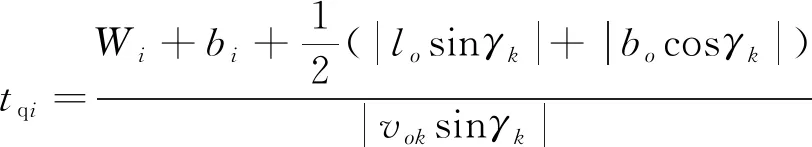
(17)

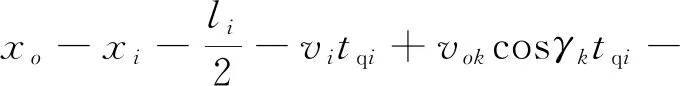
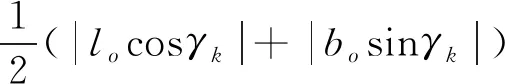
(18)

穿越船舶从第i艘船船首穿越如图7所示。

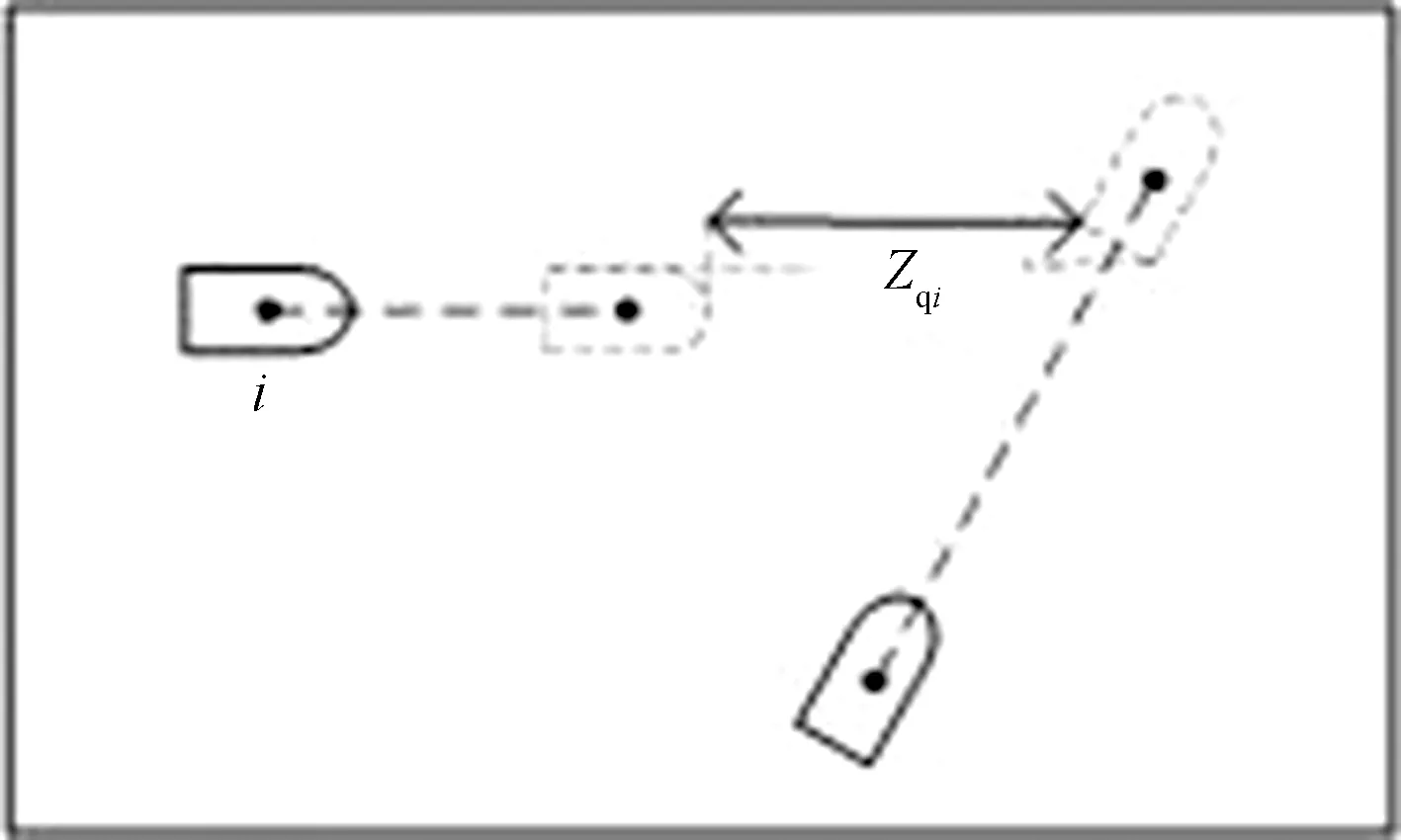
图7 穿越船舶从第i艘船船首穿越Fig.7 Cross the ship from the bow of the i-th ship

1.5.3 穿越船舶从第j艘船船首穿越

设：tqj为穿越船舶从待穿越位置航行至船尾刚刚离开第j艘船纵向(航道垂直方向)位置时刻，所需要的时间，s；zqj为穿越船舶从待穿越位置航行至船尾刚刚离开第j艘船纵向(航道垂直方向)位置时刻，与第j艘船首的距离，m。

则：

(19)

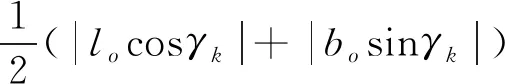
(20)

穿越船舶从第j艘船船首穿越如图8所示。

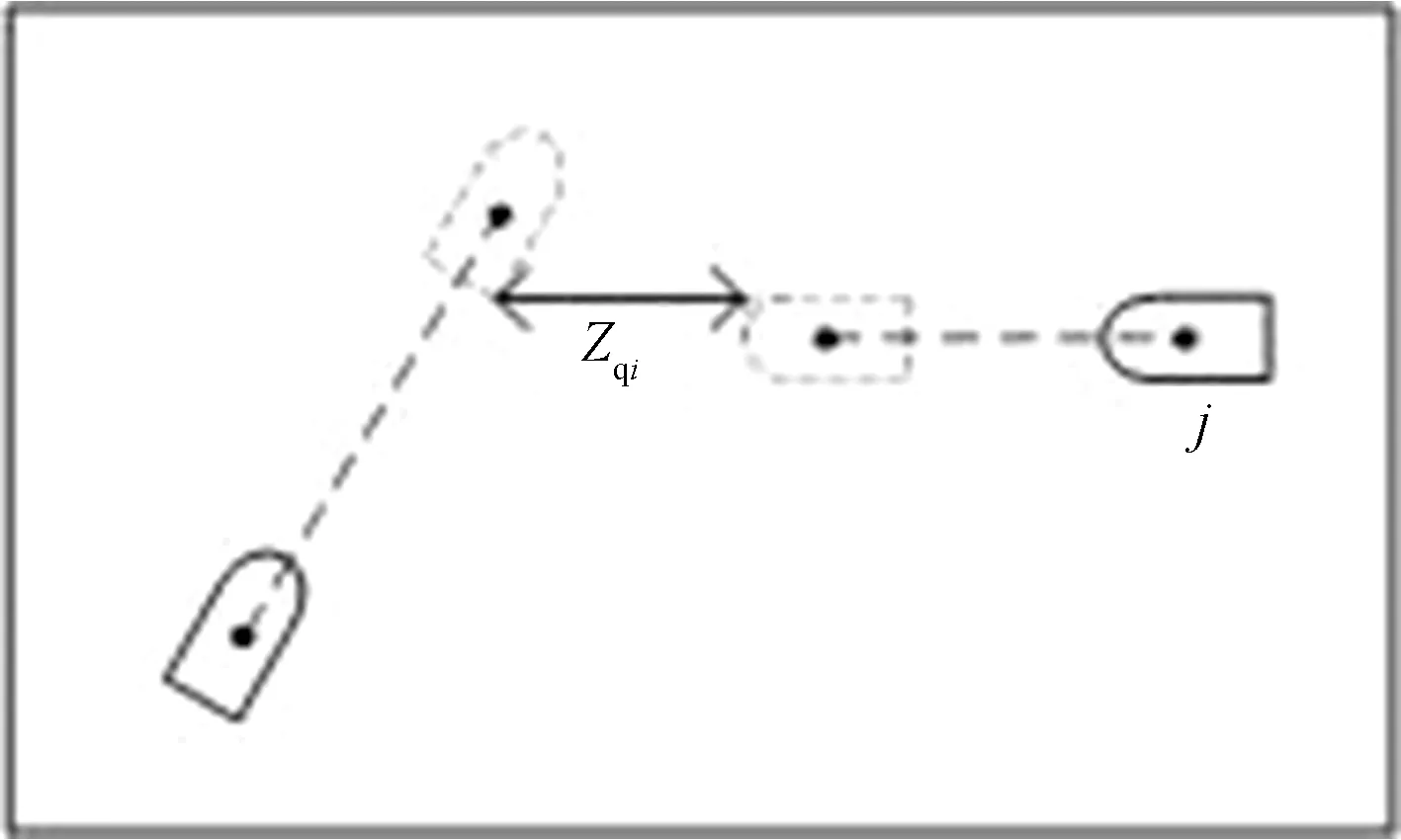
图8 穿越船舶从第j艘船船首穿越Fig.8 Crossing from the bow of j-th ship

1.5.4 穿越船舶从第j艘船船尾穿越

设：thj为穿越船舶从待穿越位置航行至船首刚刚到第j艘船纵向(航道垂直方向)位置时刻所需要的时间，s；zhj为穿越船舶从待穿越位置航行至船首刚刚到抵达第j艘船纵向(航道垂直方向)位置时刻，与第艘j船尾的距离，m。

则：

(21)

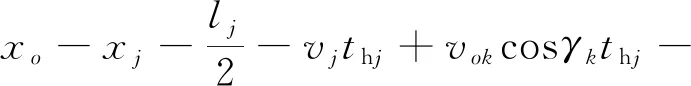
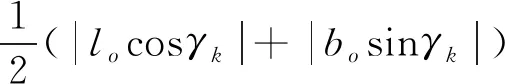
(22)

穿越船舶从第j艘船船尾穿越如图9所示。

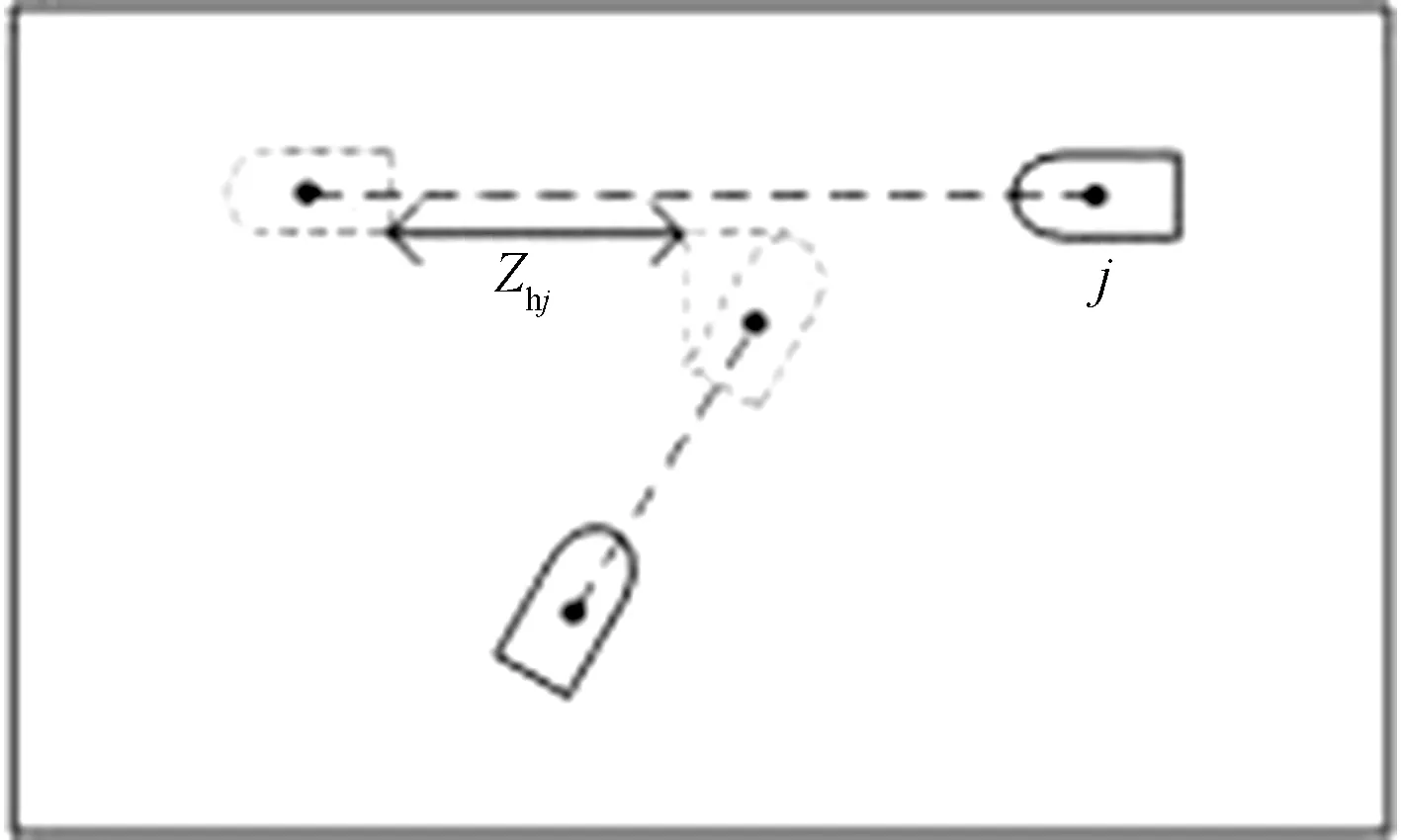
图9 穿越船舶从第j艘船船尾穿越Fig.9 Cross the ship from the stern of the j-th ship

2 判断穿越船舶是否允许穿越

2.1 判断穿越船舶某一时刻是否允许穿越

通过以上的仔细分析，发现可以将i船与j船汇总成两种情况来进行安全距离的判断：①穿越船舶从第i艘船船首穿越；②与穿越船舶从第i艘船船尾穿越。因而利用之前的计算针对i船情况的公式即可计算所有船舶。

设：hhi为穿越船舶从第i艘船船船尾处穿越，与该船的横向安全距离，m；hqi为穿越船舶从第i艘船船船首处穿越，与该船的横向安全距离，m；zi为穿越船舶从第i艘船船首或船尾穿越时，除去安全距离外，能保持的最大距离，m；Zt0为穿越船舶在t0时刻是否允许穿越，是所有船舶zi的最小值，m。

则，zqi-hqi表示穿越船舶从第i艘船船首穿越时，除去安全距离外，能保持的最大距离；zhi-hhi表示穿越船舶从第i艘船船尾穿越时，除去安全距离外，能保持的最大距离。

zi=max(zqi-hqi,zhi-hhi)

(23)

若zi<0，则表示针对i船，穿越船舶禁止穿越。

Zt0=minzi

(24)

若Zt0≥0则穿越船舶在t0时刻允许穿越，否则，禁止穿越。

2.2 判断穿越船舶在t0～tn时间内是否允许穿越

设任意时刻tn用t0+nt表示，则：计算t0的方法，就是判断穿越船舶与航道正常航行船舶是否保持安全距离的方法。

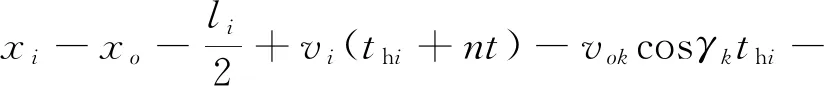
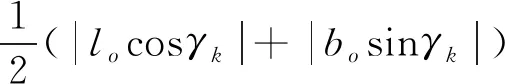
(25)

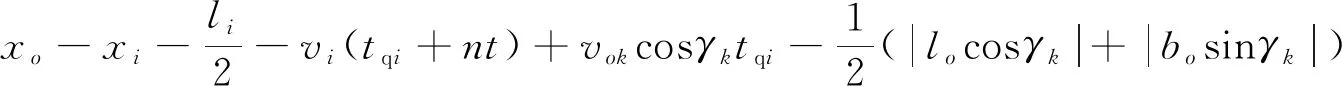
(26)

zi=max(zqi-hqi,zhi-hhi)

(27)

Ztn=min(zi)

(28)

若Ztn≥0，则穿越船舶在tn时刻允许穿越。在t0～tn时间内，若Ztn≥0，n=0～n。

Zt=max(Zt0，Zt1，…，Ztn)

(29)

则t0～tn时间内，Zt是该时间段内最适合穿越的。

3 实例验证

通过MATLAB进行对穿插模型的仿真实验。

前期通过船讯网分时段采集一段时期内的某个港口航道内的船舶数据，包括船舶的船型、船长、船宽、航行方向、船速和位置等具体信息。进行分类整理与处理，获得时段内航道内船舶的各项平均数据，作为对穿插模型的仿真的实验数据。

使用MATLAB建立一个模拟仿真航道并且随机生成船舶位置。设水道宽度为1 500 m，分为上下两个水道，上水道宽度为700 m，分为五条小航道，下水道宽度为800 m，分为六条小航道。取6 000 m长度的水道作为当前水道的计算区域。航道内船舶的数据来自于之前的船讯网统计的各项的平均数据，见表1。

表1 航道船舶数据

设穿越船舶的初始位置坐标为(0,0)，船长50 m，船宽10 m，正常船舶的航行速度为5.14 m/s，那么设穿越船舶的航速为0.514 m/s。水道中的通行船舶的船型，在长110 m、宽16 m与长59 m、宽12 m这两种常见船型之间随机选择。通行船舶的坐标则通过MATLAB程序来随机生成。

首先通过MATLAB编程随机生成所需要求的船舶数据。之后，取Δt=60 s，即1 min，取γk=90°，双向安全距离均取400 m，通过MATLAB编程计算1 h以内穿越船舶距离航道内通行船舶除去安全距离以外的最近距离。得到的计算结果如图10所示。

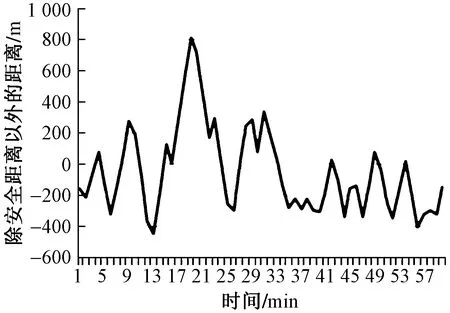
图10 安全距离以外的最近距离Fig.10 Closest distance beyond safety distance

从图10中可以得出，该情况下，穿越船舶与通行船舶保持距离最远的时刻是第21 min时，此时除去安全距离距通行船舶最近可达894.45 m。若从时间成本考虑，船舶首次可以穿越的时刻为第4 min，此时除去安全距离距通行船舶最近可达79.68 m，但是安全距离大于0的时间间隔较短，因此第8 min第二次到达安全距离且时间间隔更久，可以安全与时间更加兼顾。

若穿越船舶以不同的角度穿越，以上数据将会发生变化。分别将穿越船舶的角度向左、右偏移20°，即在穿越船舶角度γk=110°与70°的情况下，分别在之前相同船舶之间进行穿越计算，可以得到如图11所示结果。

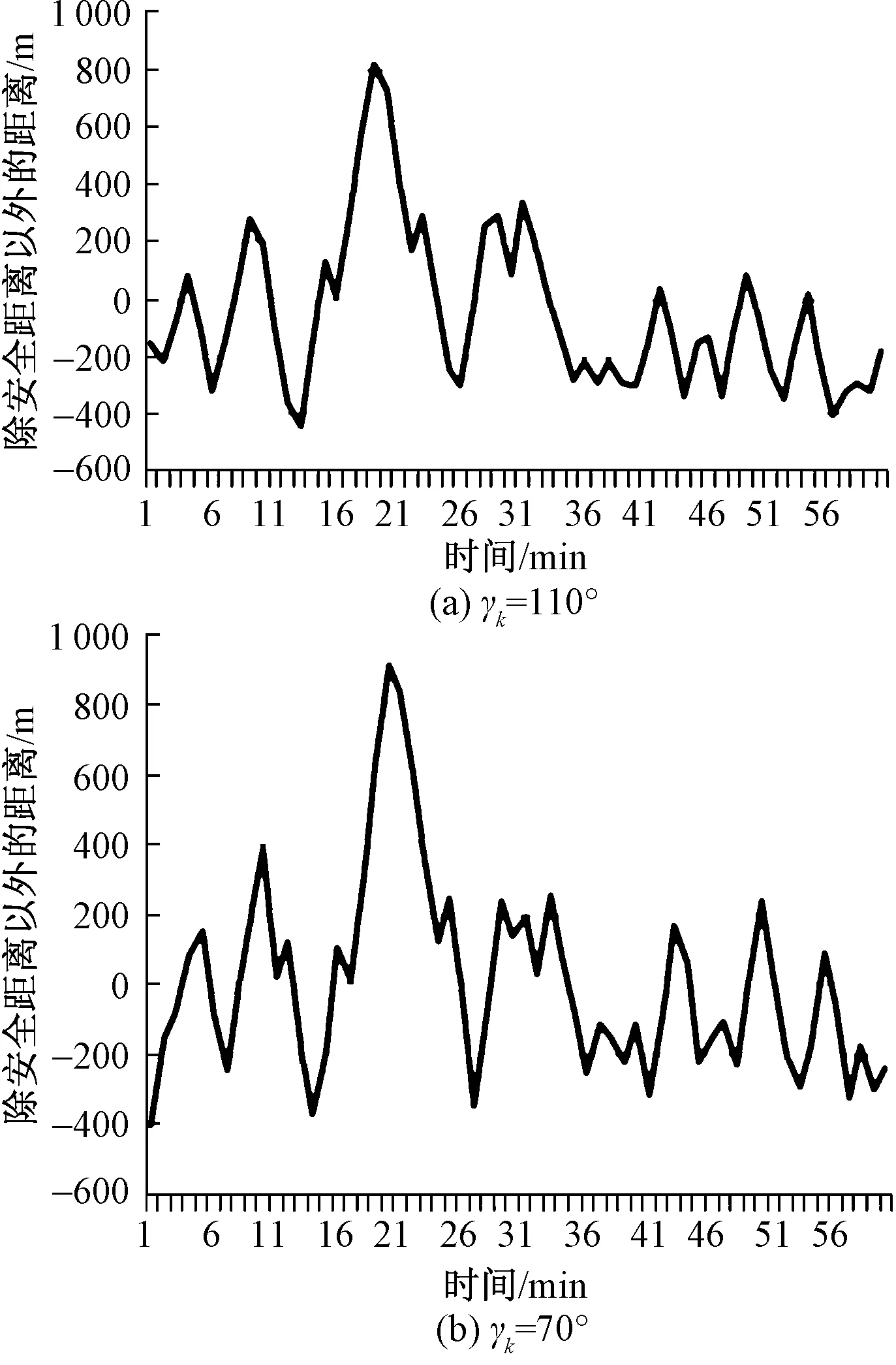
图11 γk=70°和110°时，1 h内的最近距离Fig.11 The shortest distance within 1 hour at γk=70°，110°

在γk=110°的情况下，在19 min通行船舶除去安全距离以外的距离达到最大值，为820.45 m。在4 min可以最早进行穿越，通行船舶除去安全距离以外的距离为86.96 m，但是同样的，时间间隔过短。在8 min时候，第二次穿越间隙出现，且时间间隔充足。此时，90°与110°情况下穿越情况基本相似，可以根据需要到达的位置来选择穿越角度。

在γk=70°的情况下，在20 min通行船舶除去安全距离以外的距离达到最大值，为724.55 m。在4 min可以最早进行穿越，通行船舶除去安全距离以外的距离为82.28 m，且时间间隔充足。因此在70°情况下，4 min就可以兼顾时间最早与安全性。

通过以上的算例可以看出，该模型可以有效预测水道内穿越船舶的可穿越时间与船舶之间距离。在不同穿越船舶穿越角度下，会得到不同的结果，因此可以将时间、安全、距离等不同要素。按照需要求搭配选择，以选择自己需要的理想穿越时间与角度。可以看出，该算法模型的预测精度较高、理论上能安全穿越航道的船舶穿插间隙，可以较为有效地防控船舶横越港口以及航道时候的船舶碰撞风险。

4 结论

结合船型与穿越船舶角度从防止碰撞的角度推导了船舶穿越水道的横越模型，依据穿越的角度选择合适的穿越时机可以利用良好的穿越间隙进行船舶的安全穿越；通过实测数据的统计整理建立了某港口水道的通行船舶数据，并且验证了模型的有效性，可以提高港口区域以及航道内船舶纵向穿越时的安全性，并且可以根据需求，从不同方面考虑，自由的选择安全的穿越时间。

但是研究的情景较为简单，缺乏复杂与动态情况下的深入考虑；并且是以推算分析为主，应用于实际情况中的精确性有待提高，这是今后进一步研究的方向。