基于SimMechanics的直线二级倒立摆仿真研究

余永俊， 任一峰， 安 坤， 常超勇

(中北大学电气与控制工程学院,太原 030051)

倒立摆被誉为“控制领域的一颗璀璨明珠[1]”,它的强耦合、非线性、高阶次等特性吸引了众多研究者,他们将其视为理想的实验平台用来验证各算法的可靠性,并将研究的新控制方法广泛用于航天、军工、机器人、人工智能等各领域中[2-4]。同时,在一些高等学府中,倒立摆系统也作为实验器材应用到课堂和实验中。研究倒立摆系统不仅是揭示控制论诸多特性,而且具有重大商业价值和实际意义。

近年来,中外控制界对倒立摆进行了深入钻研,研究者已用经典比例积分微分(proportional integral derivative, PID)控制、现代控制理论和各智能控制方法实现了对各级倒立摆控制[5]。但大多数研究者致力于用Simulink搭建数学模型,而利用SimMechanics 搭建三维可视化模型仿真相对甚少。SimMechanics工具箱为多体动力机械系统提供了直观有效的建模分析手段,并在仿真过程中生成系统三维动画,更便于系统的分析和验证。文献[6]使用第二代SimMechanics工具箱建立旋转倒立摆物理模型,通过极点配置、PD控制和基于线性二次型(linear quadratic regulator, LQR)控制以平衡倒立摆。文献[7]用SimMechanics建立单级倒立摆模型,通过使用线性融合将多维模糊控制转换单维模糊控制并实现倒立摆稳定。文献[8]针对单级倒立摆控制设计PID控制器,采用遗传算法(genetic algorithm, GA)和人工蜂群算法(artificial bee colony, ABC)用于调整PID控制获得最佳增益,并用于SimMechanics 模型中。文献[9]设计一种全状态观反馈控制器实现单级倒立摆SimMechanics模型控制,并表明SimMechanics可用于不稳定的非线性系统。文献[10]对单极倒立摆自摆起和平衡控制问题提出Bang-Bang控制和LQR控制,并运用于单级倒立摆SimMechanics仿真。文献[11]利用SimMechanics 工具箱建立了直线六级倒立摆模型,并利用LQR设计状态反馈控制器实现了仿真控制。

现利用第二代SimMechanics工具箱对直线二级倒立摆进行三维建模,并设计主导极点配置方法整定PID参数和基于LQR融合模糊控制进行仿真,验证两种算法的可行性并进行对比分析。

1 二级倒立摆的数学模型

忽略空气阻力和各种摩擦力之后,可视二级直线倒立摆系统是一个运动刚体系统,其简化结构如图1所示,建模过程所用物理参数意义及取值如表1所示。

图1 二级倒立摆结构Fig.1 Double inverted pendulum structure

表1 直线二级倒立摆参数Table 1 Line double inverted pendulum parameters

利用拉格朗日方程推导系统数学模型,拉格朗日方程为

式(1)中：L为拉格朗日算子；T为系统动能；V为系统势能；q为系统的广义坐标。

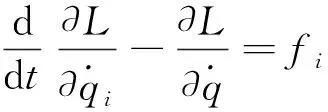
式(2)中：i=1,2,3，…，n；fi是系统在广义坐标qi方向上的广义力,在本系统中,假设系统的3个广义坐标分别是x、θ1、θ2。

系统的总动能为

系统的总势能为

V=Vm1+Vm2+Vm3=m1y1+m2y2+m3y3=

m1l1cosθ1+m2(2l1cosθ1+l2cosθ2)+2m3l1cosθ1(4)

由于在广义坐标θ1、θ2上均无外力作用,则有以下等式成立:

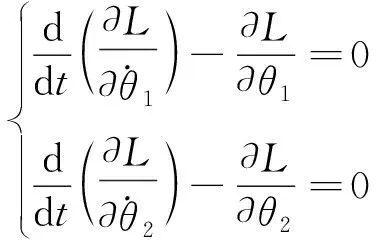
取平衡位置时各变量初值为零,在平衡位置进行泰勒级数展开并线性化,将各参数值带入,得到系统的状态方程为

2 倒立摆SimMechanics模型

SimMechanics是Simulink的一个建模工具箱,可以按照物理学原理对刚体系统进行建模和仿真[12]。并包含了一系列带有坐标系变换、静力学约束、驱动、铰链等系统原件用以搭建和求解实际物理系统的模型,并能与Simulink设计的控制器连接进行综合仿真。SimMechanics有一代和二代,由于第二代模型相对直观,能够直接建立机械结构的几何特性,因此将采用第二代工具箱进行模型构建。基于上述建立的数学模型,可构建倒立摆SimMechanics结构如图2所示,可视化模型如图3所示。

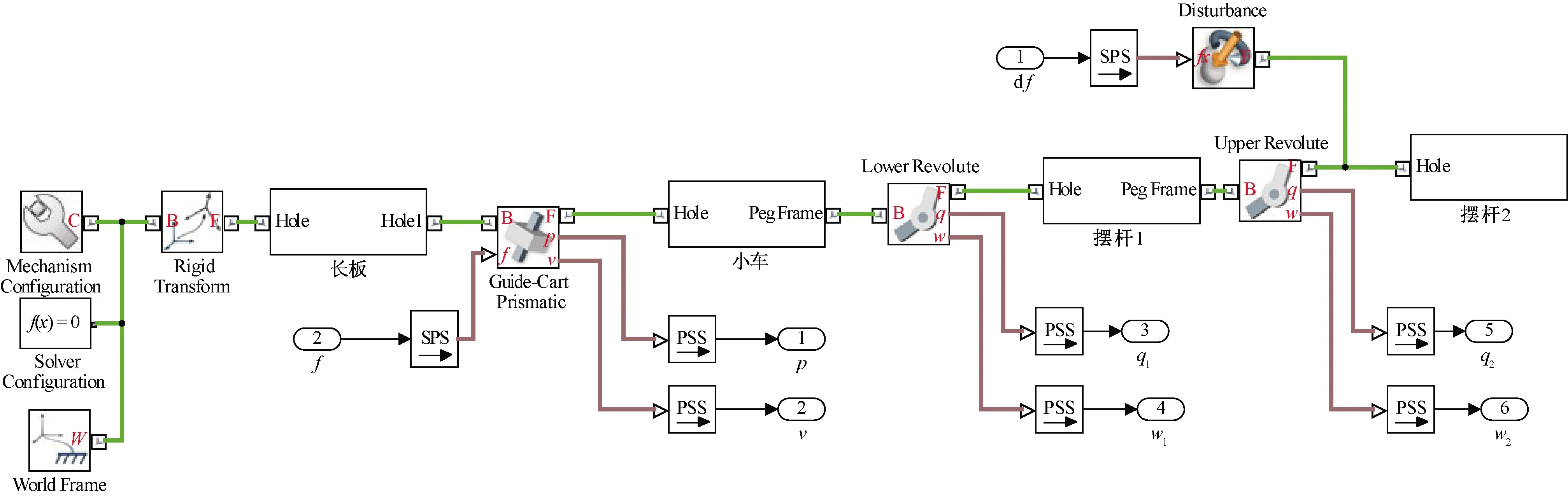
图2 倒立摆SimMechanics模型Fig.2 Inverted pendulum SimMechanics model

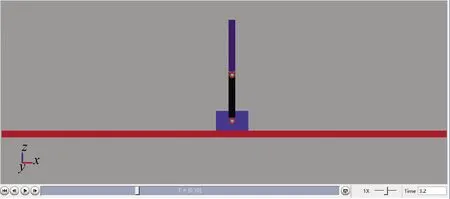
图3 倒立摆可视化模型Fig.3 Inverted pendulum visualization model

图2中,Mechanism Configuration是机构配置模块,用于整个机器的机械和模拟参数；Configuration和World Frame分别是机构求解和世界坐标系；上述3个模块是构建任何模型的基础。Rigid Transform是两个结构体进行连接的模块；Revolute Jonit是连接两根摆杆间的转动模块；SPS是将单位的仿真输入转变为物理输出,PSS则相反；而长板、小车、摆杆1、摆杆2是各模块子系统，里面集成了Solid刚体模块和坐标系连接；Solid表示将几何图形、惯性和质量以及图形组件合并为单个单元实体；Disturbance 是指在所附的框架上应用外部力和扭矩。p、v、q1、w1、q2、w2是输出,分别代表小车位移、小车速度、摆杆1角度、摆杆1角速度、摆杆2角度、摆杆2角速度。f为输入,df为加在第2根摆杆的扰动。

3 倒立摆SimMechanics模型仿真

3.1 PID控制算法仿真

由构建的倒立摆SimMechanics模型(图2)可知,直线二级倒立摆是单输入多输出系统,而PID是单变量调节器,一般用来研究单输入单输出系统。一个PID调节器只能控制一个输出。而在整个倒立摆系统中,系统的输出为小车位移、摆体1偏角和摆体2偏角,所以需要用3个PID调节器构成并联形式分别对倒立摆系统的小车位移、一二级摆体偏角进行控制。由于倒立摆系统对响应速度有一定要求,而积分调节器会导致系统稳定性降低,动态响应变慢。因此,将整个系统加入3个PD调节器构成闭环反馈控制,PID控制仿真结构如图4所示。

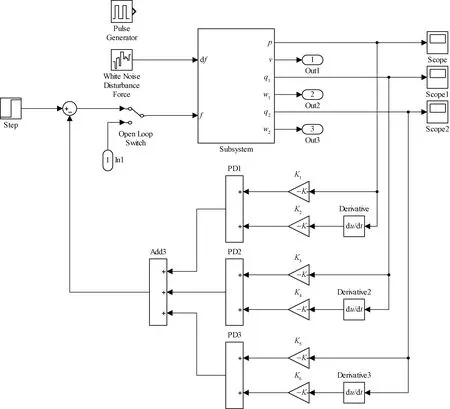
图4 倒立摆PID控制Fig.4 Inverted pendulum PID control

由PID控制结构可知,待整定参数为K1～K6。这6个参数与倒立摆状态变量一一对应,分别为小车位移、小车速度、摆杆1偏角、摆杆1角速度、摆杆2偏角、摆杆2角速度。仔细发现PD控制倒立摆结构与状态反馈控制结构类似,又因倒立摆系统是完全能控能观的,根据文献[13]可以通过极点配置确定三路PD控制器的6个参数,而笔者想到了用主导极点配置进行PD控制器的参数整定。 系统中Subsystem是倒立摆SimMechanics模型封装的子系统,并对df扰动输入加入了脉冲干扰模块,并改变脉冲幅值的大小,确定PID控制所能控制最大脉冲干扰幅值。K1～K6参数根据主导极点配置去确定,即选取一对靠近虚轴主导极点,其他极点远离该主导极点。这里选取极点为P=[-2±2i -20±4i -18±6i],利用MATLAB中place函数求得K1～K6参数为K1=82.212，K2=57.232，K3=-180.392，K4=-33.506，K5=-521.915 6，K6=-38.690。

设置倒立摆初始位置为摆杆1:10°,摆杆2:-10°,其他状态变量为0，得图5所示仿真曲线。

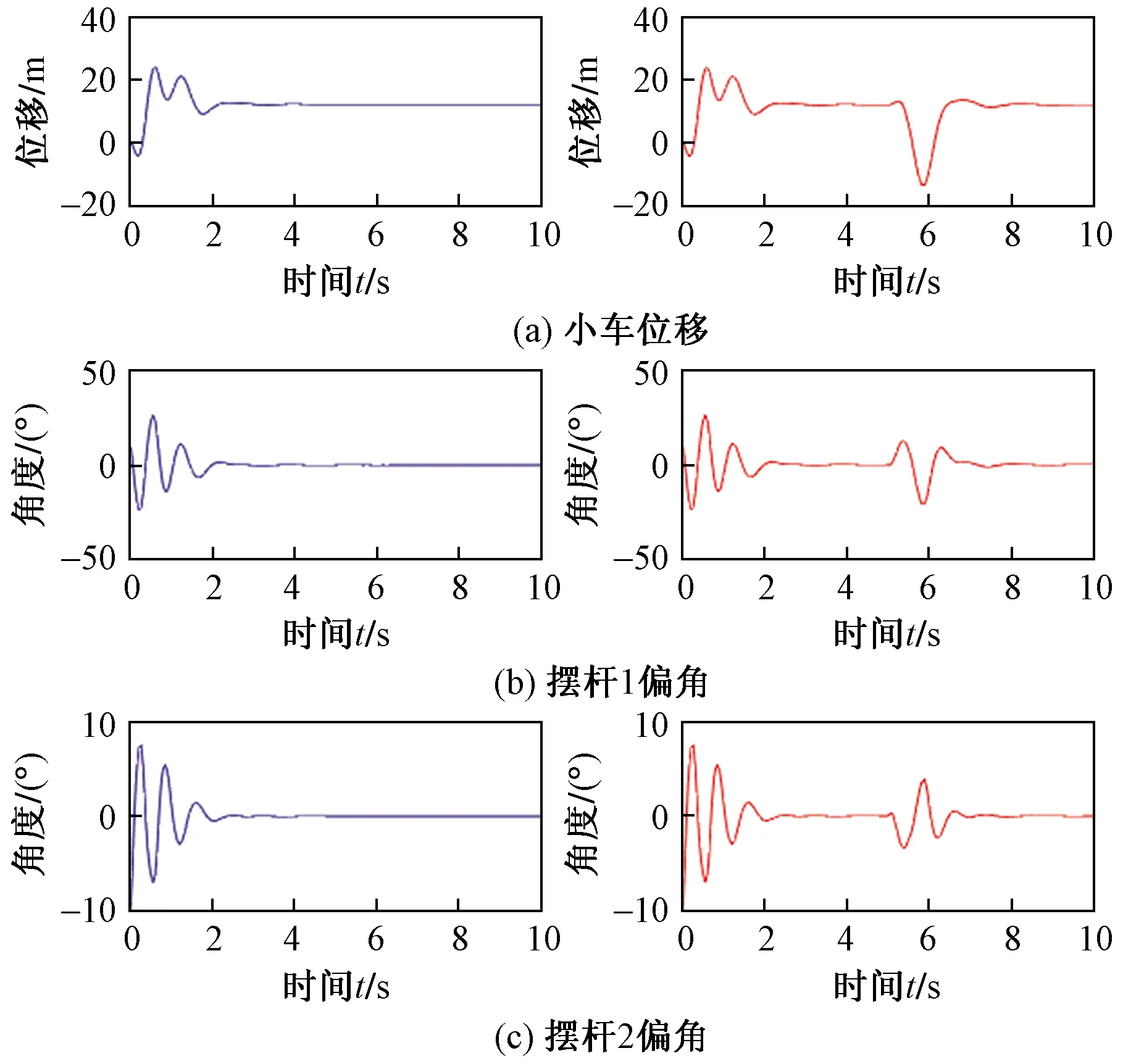
图5 PID控制仿真曲线Fig.5 PID control simulation curve

由图5可知,系统调节时间大约在2.3 s,超调量较大,延迟5 s后加入脉冲干扰,小车来回振荡几次后又回到稳定状态,因此,系统具有一定抗干扰能力,而PID控制所能控制最大脉冲干扰幅值为0.1 N。且采用主导极点配置整定PID参数方法要比传统极点配置整定PID参数动态性能更优。

3.2 模糊控制算法仿真

由于二级倒立摆系统有6个状态变量,如果每个变量的论域有7个模糊子集,那么将有上万条规则,引起模糊规则爆炸。现利用LQR算法来构造融合函数[14]，可以有效地简化模糊控制器设计,采用融合函数模糊控制器框图如图6所示。

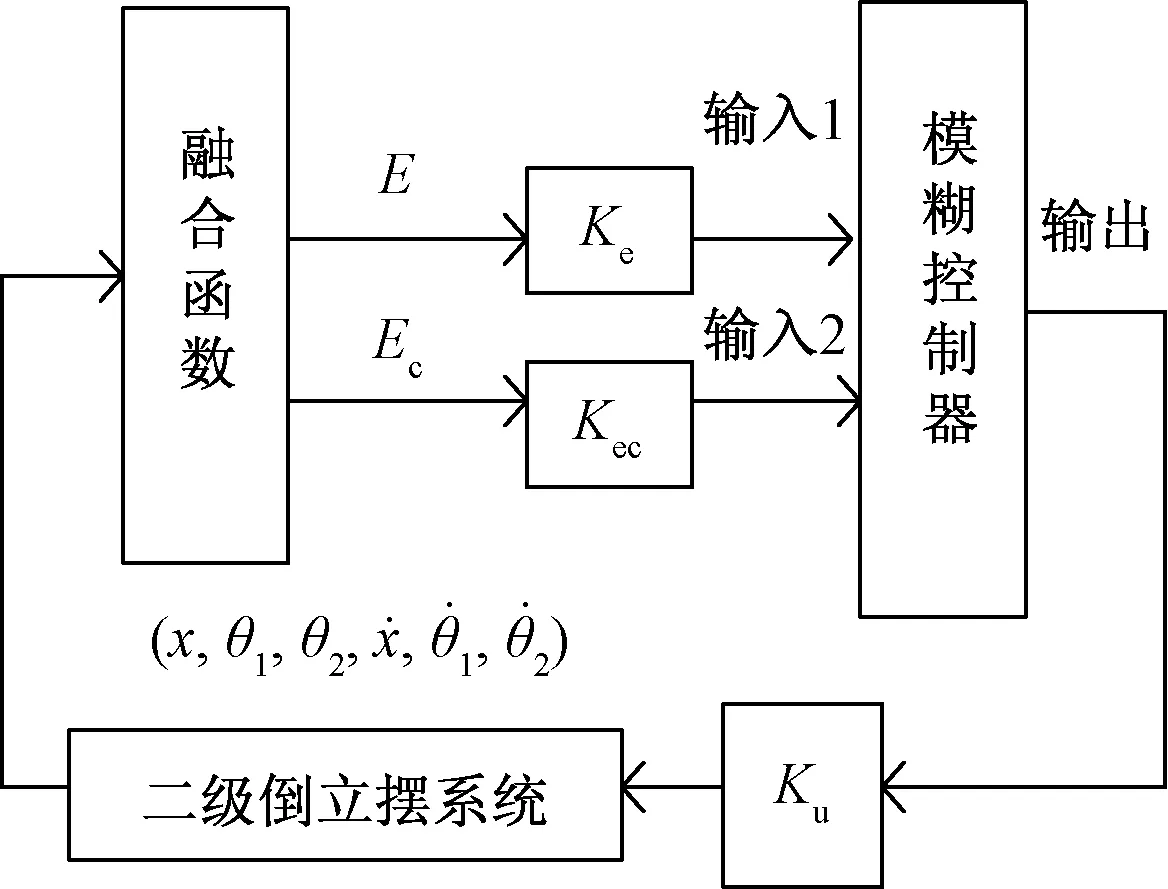
图6 模糊控制系统框图Fig.6 Fuzzy control system block diagram

3.2.1 融合函数设计

根据LQR算法,取Q=diag(500,500,500,0,0,0),R=1,利用K=lqr(A,B,Q,R)函数,求得K=[22.360 7 18.246 2 -50.811 6 -14.482 0 -278.729 8 -20.584 1],进而构造融合函数F1(x)为

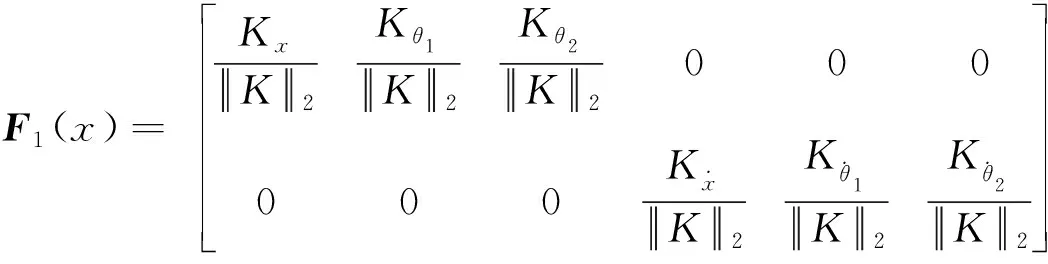
式(7)中:

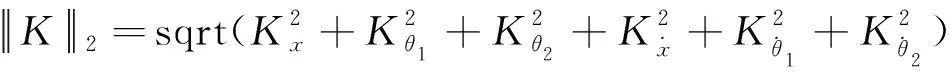
通过F1(x)把6个状态变量降维,融合得到综合误差E和综合误差变化率Ec，即

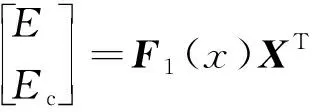
可算出:

F1(x)=

3.2.2 模糊控制器设计

根据经验,确定综合误差E的论域为E=[-6 6],误差变化率Ec的论域为Ec=[-6 6]；输出控制量U的论域为U=[-6 6]；此外,设置每个变量论域为7个模糊子集,符号表示为[NB,NM,NS,ZE,PS,PM,PB]。对控制及输入变量的属度函数选择均为“三角形”,得到表2所示模糊控制规则表。

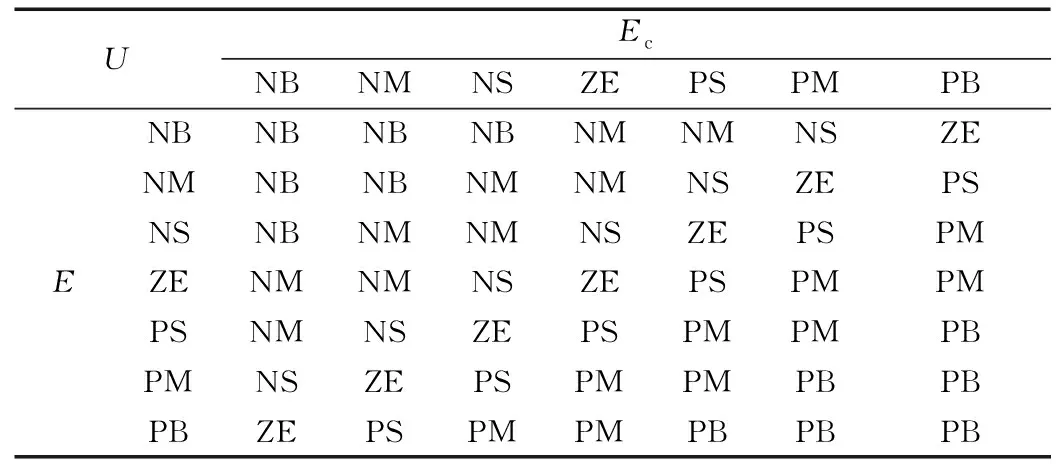
表2 模糊控制规则表Table 2 Fuzzy control rule table

3.2.3 模糊控制仿真

采用基于LQR融合函数降低模糊控制维数的Simulink仿真结构如图7所示,并根据大量实验及试凑,确定量化因子及比例因子系数为:Ke=25,Kec=18,Ku=30。所得仿真曲线如图8所示。

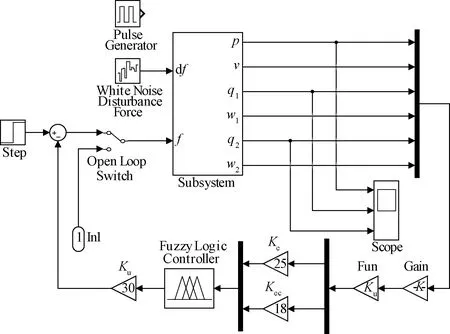
图7 模糊控制结构Fig.7 Fuzzy control structure

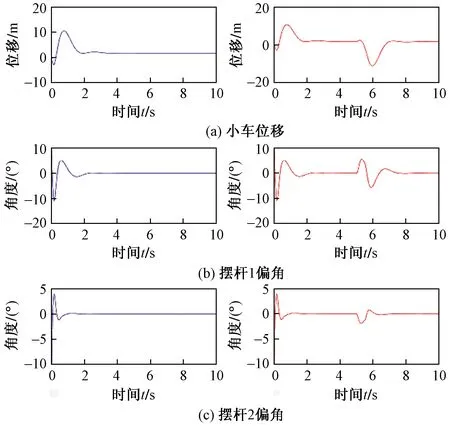
图8 模糊控制仿真曲线Fig.8 Fuzzy control simulation curve

由仿真曲线可知,小车位移调节时间约2.2 s,摆杆1、摆杆2偏角约1 s,因此模糊控制有很好的快速性,系统略有超调但振荡不是很剧烈,且模糊控制能控制最大脉冲干扰幅值是1.1 N,具有很好的抗干扰能力。

4 仿真结果对比分析

用两种控制算法对倒立摆SimMechanics模型进行了仿真,都能进行稳摆控制,且都具备一定的抗扰动能力。为了对比两种控制算法的控制性能,得到图9所示对比曲线。

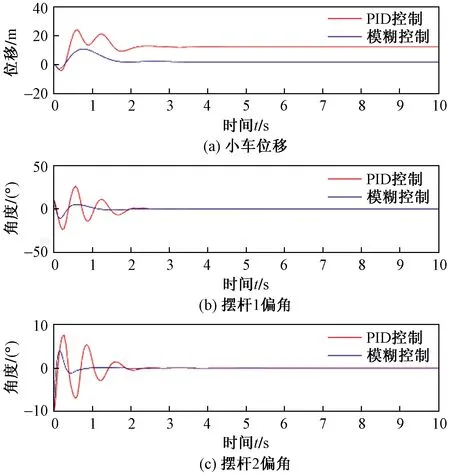
图9 控制算法对比曲线Fig.9 Control algorithm comparison curve

(1)动态性能分析:无论是超调量还是调节时间,模糊控制动态性能都优于PID控制,且PID控制要比模糊控制震荡剧烈。

(2)抗干扰分析:PID所能控制最大脉冲干扰幅值为0.1 N,而模糊控制是1.1 N,幅值大小即扰动力大小,因此,模糊控制具备更好的抗干扰能力。

(3)稳态误差分析:由小车位移曲线可知,进入稳态后,模糊控制可以回到初始位置,而PID偏离初始位置,因此,模糊控制稳态精度更高。

5 结论

围绕直线二级倒立摆系统,建立了其数学模型及SimMechanics可视化模型,通过仿真验证了PID和模糊控制算法都能对倒立摆进行稳摆控制,由仿真曲线及直观观看可视化动画,可知模糊控制无论是在动态性能、抗干扰能力和稳态精度上都比PID控制性能好,这体现了模糊控制的智能性,并为下一步倒立摆实物控制打下了理论基础。