基于先验知识的降维自适应时域滤波器

董晨曦， 陈华丽

(武汉科技大学信息科学与工程学院,武汉 430081)

机载预警(airborne early waming, AEW)雷达一般飞行高、速度快,具有灵活的机动性、宽广的探测范围,是未来战争中夺取制空权的关键。但是由于高速移动和探测范围广,导致机载雷达面临复杂的杂波环境,其探测性能受限于复杂的干扰[1]。空时自适应处理(space-time adaptive processing, STAP)[2-3]通过空域和时域两个维度联合处理环境干扰,能有效地提高检测机载雷达抑制地杂波检测目标的能力。但是实际处理时受限于独立同分布(i.i.d.)样本和计算量的问题,很难达到最优的性能。一个相干处理时间内有K个脉冲,N个等距线阵,直接采用全维STAP处理,计算量达到了O(K3N3),需要的设备量和运算量在实际中难以实现。为了能满足实际的处理要求,降维STAP技术在机载雷达中广泛运用。

降维STAP方法,如经典的因子法(factored approach, FA)、扩展因子法(extended factored approach, EFA)[4-5]等也可称为因子化降维STAP方法,通过采用先在时域通过多普勒滤波器处理然后在空域自适应处理的方式,将全维自适应处理的问题转变成了在K个多普勒通道分别自适应处理的问题,它们通过适当降低系统自由度的方法,不仅大大地降低了运算量和对独立同分布样本的需求,也保证了STAP的性能达到次最优。先验知识能够提高机载雷达的处理性能[6-7],当机载雷达的速度和工作参数确定时,再结合数字地形信息,可以先验已知雷达的地、海杂波功率谱[8]。文献[9]提出了基于先验知识的空时自适应处理,将降维STAP与机载雷达环境的先验知识结合起来,提高机载雷达探测能力。文献[10]将先验信息与自适应功率剩余(adaptive power remaining, APR)检测方法相结合,解决了均匀训练样本选择性能。文献[11]将先验知识与稀疏恢复相结合,抑制了机载STAP中目标方向的伪目标。文献[12]将先验知识和稀疏迭代结合起来,提出了基于先验知识的稀疏迭代STAP算法,精确杂波协方差矩阵的估计。

上述方法核心思想都是考虑将先验信息的资源用在杂波协方差矩阵的均匀估计上。本文方法考虑将先验知识和时域滤波器设计相结合,充分利用时域的自由度,改善降维处理时机载雷达的检测性能。通过先验知识,结合自适应抑制干扰和固定束宽的思想,并利用凸优化工具[13],将频率分块约束于各种多锥面不确定集和球形不确定集中,从而设计一组旁瓣和凹口可灵活调节的时域滤波器。计算机仿真表明,设计的时域滤波器有较好的鲁棒性和抗区域干扰的能力,并且可进一步降低杂波的自由度,改善降维STAP的性能。

1 传统STAP算法和因子化降维STAP算法

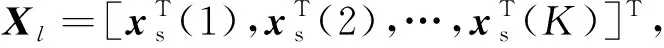
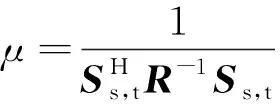
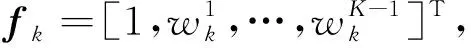
式(1)中：IN是N×N的单位矩阵。如果目标相对机载雷达运动的径向速度为v0,方位角为θ0,俯仰角为φ0,则目标回波为

s=σ0cs0⊗ct0(2)

式(2)中：σ0是目标回波幅度；cs0和ct0分别为目标的空域导向矢量和多普勒导向矢量,cs0=[1,ejws0,…,ej(N-1)ws0]T,ct0=[1,ejwt0,…,ej(K-1)wt0]T。目标经过第k个多普勒通道滤波后的数据变成：

FA处理就是保证在第k个多普勒通道的目标信号能量不变的情况下使输出信噪比最大,即如下代价函数：

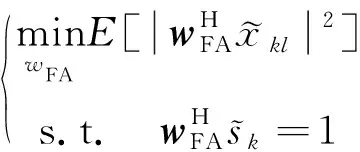
式(4)的最优解析解为

经典的时域滤波器是将动目标显示(MTI)与DFT权值结合起来处理[4],这样不仅可以在主杂波中心产生深零陷,也可以通过锥消处理限制旁瓣电平。但是实际杂波谱都会展宽,MTI+DFT的方式不能保证杂波区都产生深零陷,并且锥消处理也无法处理区域压制性干扰。

经典的时域滤波器没有充分利用时域自由度,基于先验知识就可以估计地杂波的协方差矩阵RKA[8],再利用MVDR算法,可以得到时域滤波器权值Wk-MVDR为

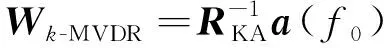
式(6)所设计出来的时域滤波器稳健性差,无法生成宽凹口,在面对区域压制性干扰时性能变差。

2 基于先验知识的时域滤波器设计

2.1 基本原理

利用先验知识,查询机载雷达的工作环境参数,结合数字高程模型,估计地杂波的协方差矩阵[15]。然后利用这些信息,划分需要约束的主瓣、旁瓣范围及对应的电平大小等信息,再利用二阶锥模型[16]构造时域滤波器的代价函数形式：

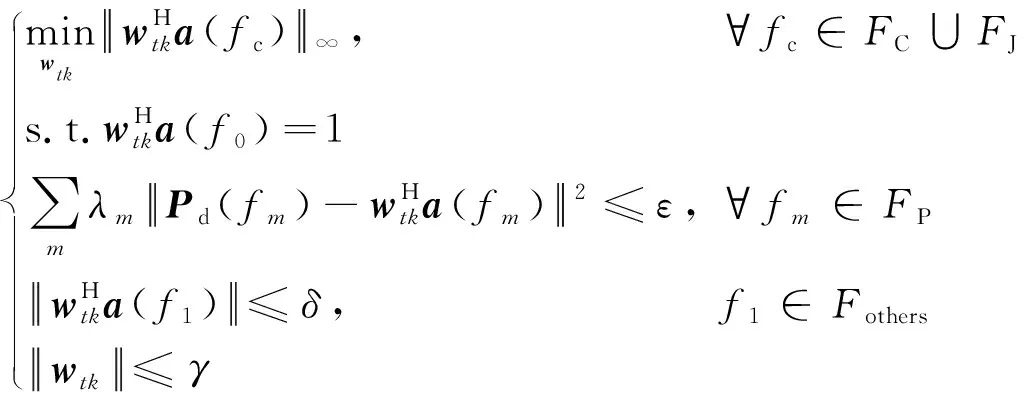
通过先验知识查询机载雷达工作环境参数,据此确定主杂波所在的多普勒通道等信息,然后据此确定时域滤波器的频率分配区域。对第k个多普勒通道,重写式(7)得：

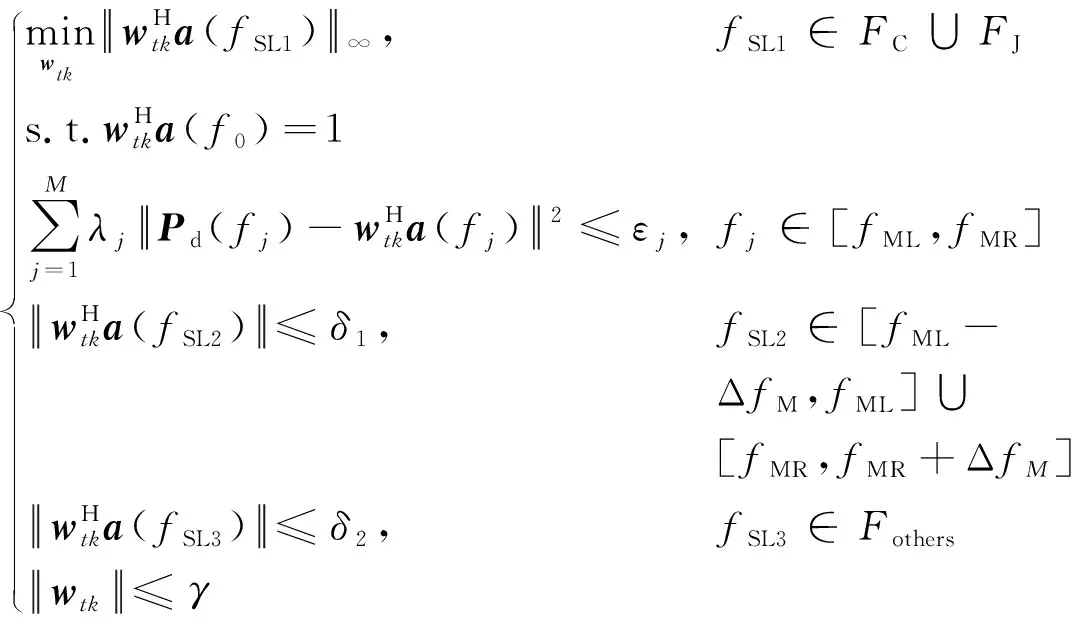
式(8)中：根据先验信息得到主杂波的多普勒频率集FC;根据传统测向技术[17],估计出FJ;fML和fMR分别指主波束左边第一个零点和右边第一个零点对应的频率,可根据中心频率f0和Pd的频率范围间接得到；主杂波的多普勒中心频率fz为2vcosψ0/λfr,其中v是载机速度,ψ0为空间锥角,λ是信号波长,fr是脉冲重复频率；通过中心频率f0和主杂波fz的靠近程度灵活调节主瓣附近的第一旁瓣范围[fML-ΔfM,fML]∪[fMR,fMR+ΔfM],ΔfM是第一旁瓣的区间大小；δ1、δ2是约束值。

ΔfM越大,需要的系统自由度越多,因此ΔfM往往取1～3个单位频率大小。 同时,δ1与δ2不能取的太小,保证系统能有足够多的系统自由度,用来在主杂波、干扰等区域形成深、宽凹口。

2.2 具体设计步骤

(1)根据先验知识,查询机载雷达的工作参数,包括机载雷达天线分布方式,机载雷达时域主波束对应的中心频率f0等,并计算主杂波归一化多普勒中心频率fz。

(2)根据步骤(1)中的参数,灵活设计时域滤波器各项参数,包括期望逼近的时域滤波器主瓣波束向量Pd,主瓣附近的第一旁瓣电平δ1和其余旁瓣部分电平δ2,白噪声增益约束值γ,主杂波、干扰的频率范围集FC、FJ,期望波束主瓣多普勒通带频率集FP。

(3)利用式(7),结合步骤(2)中的参数,设计时域滤波器,再利用MATLAB中的CVX工具箱[13]求解最优权值wtk。

(4)将wtk代替式(1)中的fk,然后再结合式(2)～式(5)就可以算出因子化降维STAP处理之后的结果。

2.3 仿真分析

仿真进行了3种时域滤波器设计方法和因子化降维STAP相结合下的性能分析。3种时域滤波器方法分别在第1节中提到的MTI+DFT滤波器和基于先验知识的MVDR滤波器,以及第2.1节中提到的通过先验知识改进的时域滤波器。并且充分考虑机载雷达在夺取制空权时面临的复杂自然及人为环境,还在仿真中添加了强的无意干扰和区域压制性干扰。所设计的时域滤波器除了能在多普勒维抑制地杂波外,还能改善来自于空域主波束方向的区域压制性干扰和无意干扰。设定机载天线按照16×16的正侧视面阵方式排列,相干积累脉冲数为32,天线阵主波束指向(90°,0°),杂噪比CNR为60 dB,添加归一化多普勒频率f11=-0.5,JNR11=30 dB的无意干扰和归一化多普勒频率f12∈[0.5:0.6],JNR12=50 dB的区域压制性干扰。

图1所示是采用本文方法改进的因子化降维STAP处理的空时二维响应图；图2是图1对应的-100 dB 处的等高线图,其中干扰1就是无意干扰位置,干扰2表示区域压制性干扰位置,并且考虑到干扰在空域主波束方向时会造成自适应方向图畸变,因此为了对比说明本文方法在恶劣情况下的性能好坏,仿真分析都是基于干扰在天线主波束方向上。对照图1的图例,可以发现所提方法能在杂波脊处形成深零陷,再结合图2的-100 dB等高线图,可以看出本文方法还能够在干扰方向上形成了深凹口抑制。

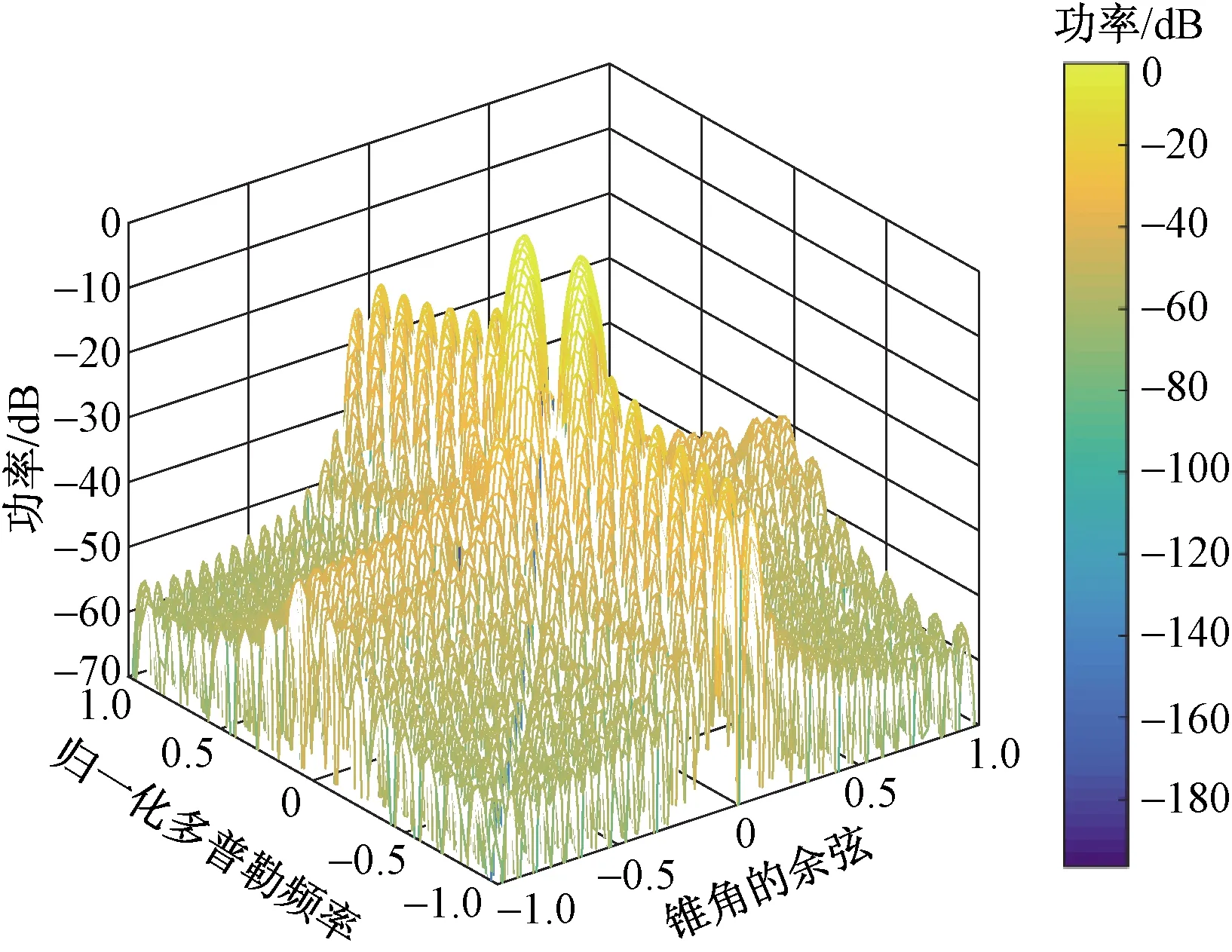
图1 空时二维响应图Fig.1 Space-time two-dimensional response map

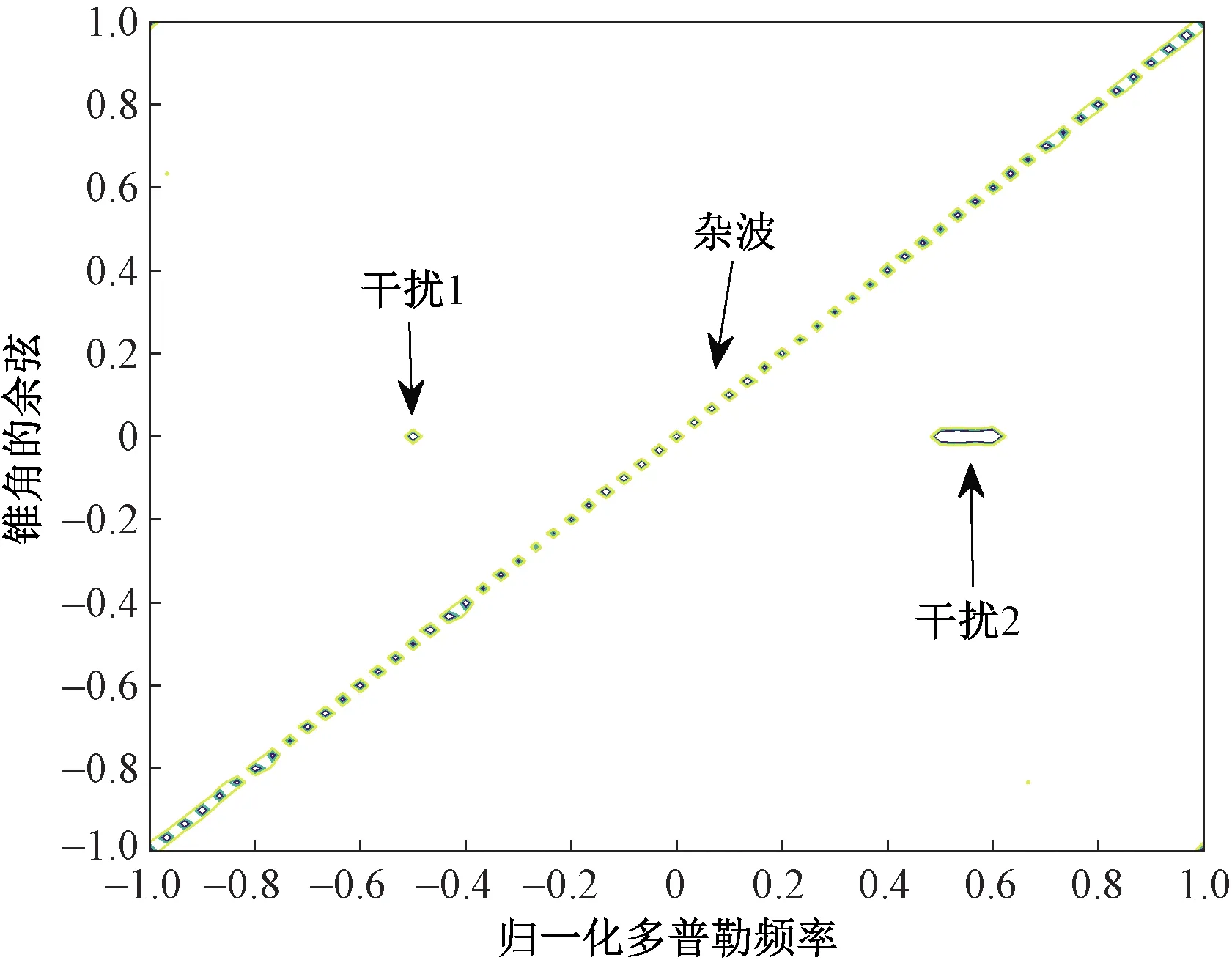
图2 -100 dB等高线图Fig.2 -100 dB contour map

图3所示是在归一化多普勒通道为f0=-0.7时的时域滤波器响应图,图4是3种时域滤波器响应图的对比图。在图3中,δ1取0.03,δ2取0.1,γ取1,误差加权系数都为1,εj是一组非负标量,为了让引入的期望主瓣具有实际的物理意义,这里选取常规DFT加-40 dB的Chebyshev窗得到的主瓣系数；图4中的MVDR方法所用谱宽和功率与本文方法的先验知识一致。观察图4,本文方法生成的主瓣与期望的主瓣吻合,本文方法能在主杂波和干扰处产生对应的可调节深凹口,而其他方法不能像本文方法一样灵活控制系统自由度的分配,导致无法生成与杂波和干扰完全匹配的深凹口。

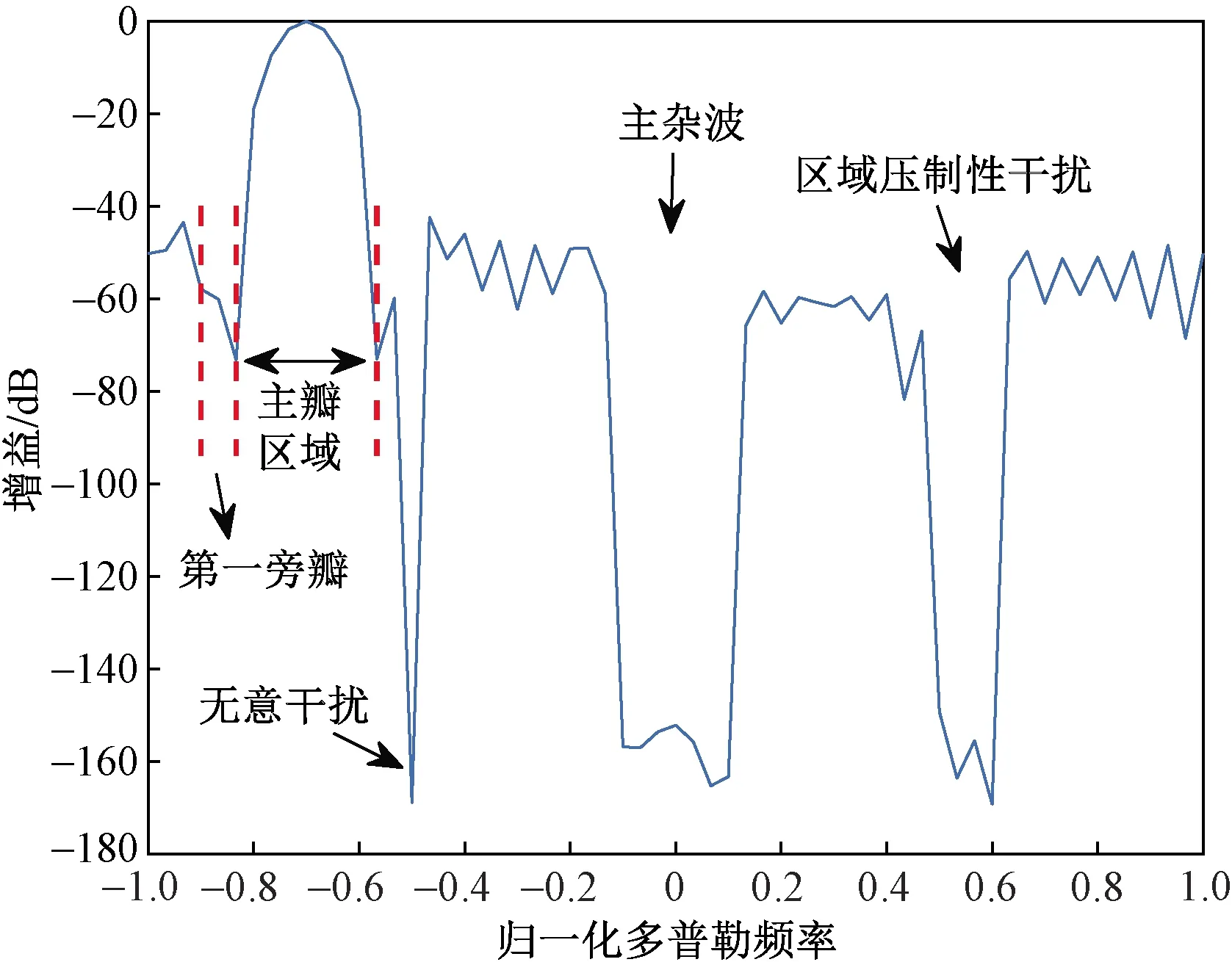
图3 本文方法时域滤波器曲线Fig.3 Time-domain filter curve of the method presented in this paper

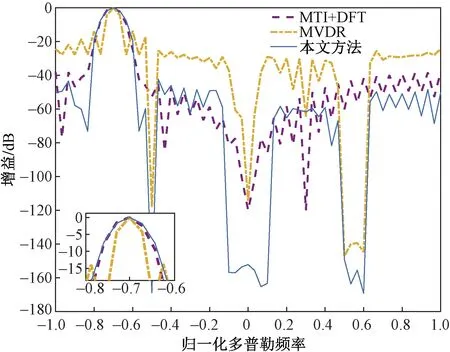
图4 3种时域滤波器对比曲线Fig.4 Three time domain filter comparison curves

本文方法不仅具有稳健性,还有可靠性。为了说明本文方法的可靠性,将前述仿真条件归纳为情况1,并另添加一组独立的仿真条件,归纳为情况2。情况2的具体内容为,添加归一化多普勒频率f21=[0.5,0.8],JNR21=30 dB的无意干扰和归一化多普勒频率f22∈[-0.4:-0.3],JNR22=50 dB的区域压制性干扰,设计情况2的时域滤波器时,除了FJ根据情况2进行调整,δ1、δ2、γ和εj等参数都和情况1一样。为了说明本文算法的稳健性,对情况1和情况2都添加阵元增益服从N[0,0.05]的高斯分布,阵元相位误差服从N[0,(5/180)2]的高斯分布。

观察图5(a),在恶劣的主瓣干扰情况下,通过最优STAP也会出现波形畸变,因此最优STAP也无法得到理想的改善性能,但本文方法相比其他方法都更加趋近最优STAP的变化曲线,特别是在干扰附近。情况2相对于情况1,区域压制性干扰和无意干扰的频率范围都发生了变化,但为了说明本文算法的可靠性,除了FJ进行对应调整外,情况2对应的时域滤波器其他参数和情况1相同。观察图5(b),本文方法相比其他方法,改善因子更趋近于最优STAP。

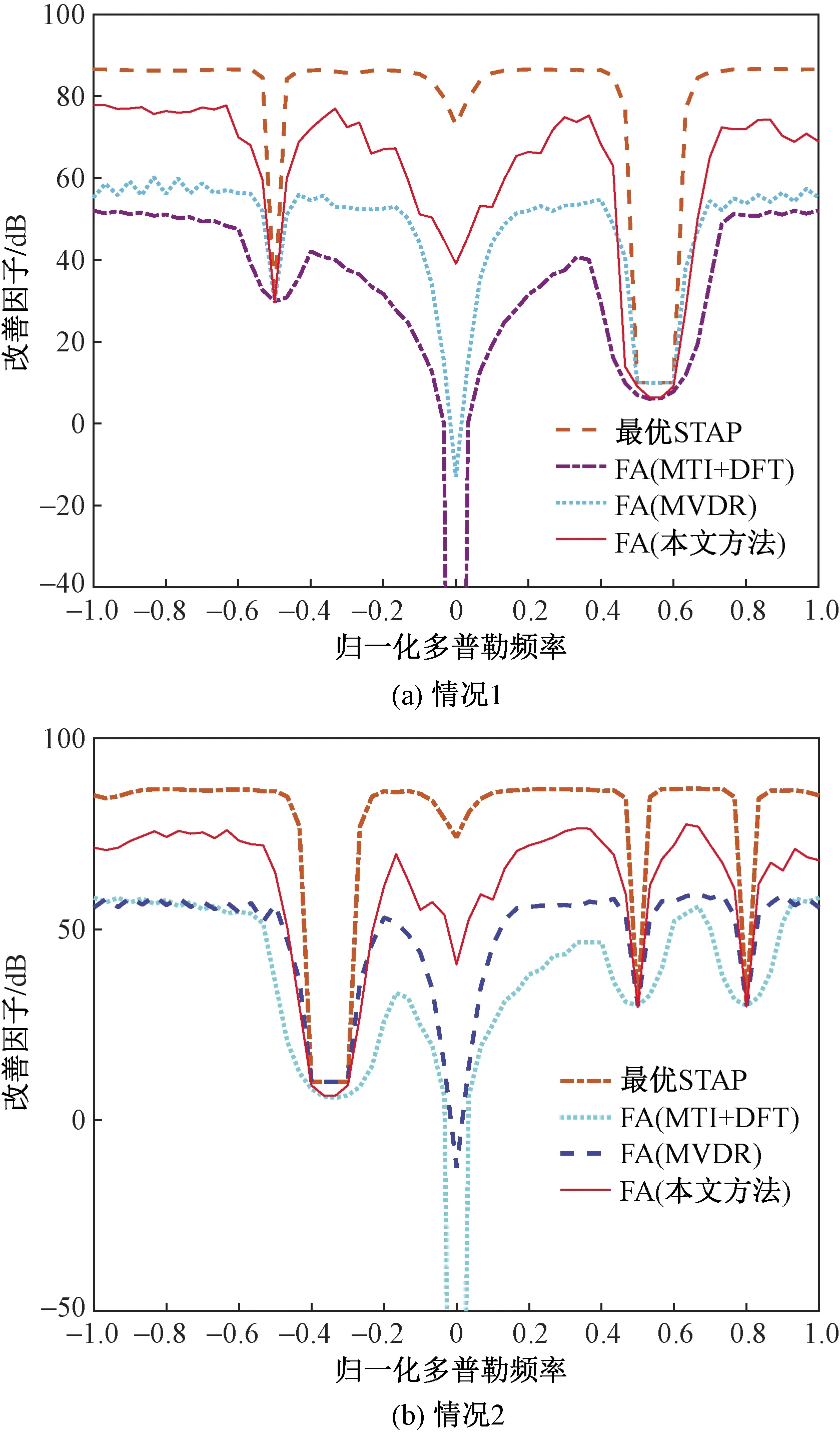
图5 改善因子Fig.5 Improvement factor

虽然实际雷达中,幅相误差主要存在于阵列的空域信号处理当中,表面上看与本文所提的时域滤波器没有直接关系。但是在STAP中,由于接收信号空时耦合的关系,因此在降维处理中,当所设计的时域滤波器性能更优时,在空域所需抑制的剩余杂波和干扰越少。所以存在幅相误差时,在空域处理过程一样的情况下,改善因子的大小可以反映时域滤波器的性能好坏。

3 结论

充分利用先验知识提供的信息,对降维STAP的时域部分有针对地设计时域滤波器。通过仿真及分析可以得出如下结论。

(1)利用先验知识,机载雷达所处环境的杂波功率谱、协方差矩阵都可估计,再利用传统侧向技术,估计干扰的大概信息。利用这些先验知识,设计可以调节时域输出增益的时域滤波器,实现对杂波和干扰的抑制。

(2)本文方法是通过适当的调节主瓣能量和感兴趣区域的能量,保证系统将剩余自由度全部用在抑制杂波和干扰上,并且本文方法还可以提高系统的稳健性。

(3)利用凸优化的手段需要较大的计算量,但本文方法是基于先验知识设计时域滤波器,时域滤波器的系数可以离线计算。