基于支持向量机回归的曲面零件涡流测距标定方法
陶正瑞, 党嘉强, 徐锦泱, 安庆龙 陈 明, 王 力, 任 斐
(1. 上海交通大学 机械与动力工程学院; 机械系统与振动国家重点实验室, 上海 200240; 2. 上海航天设备制造总厂有限公司, 上海 200245)
随着无损检测技术的发展,涡流检测以其具有非接触、无污染、易于实现自动化等优点在航空航天可靠性检测、铁道车辆及轨道质量检测、发动机包覆层、金属基体材料表面油漆等涂覆层厚度测量中有着广泛的应用[1].根据经典的涡流位移测量理论[2-3],涡流位移传感器只能测得物体表面一部分区域(1.5~2倍探头盘径)到传感器探头端面的距离.因此当被测表面为平面时,可以获得比较理想的结果,但涡流测距问题的研究对象正由平面向复杂曲面方向发展.目前,涡流测距是建立在线圈平板互感效应上的一种无损检测方法,被测金属表面为平面时可获得理想的测量精度.然而在实际应用中,涡流位移测量问题的研究对象正由平面向曲面发展,使用平板标定结果测量曲面零件精度往往达不到要求,基于曲面近似平面的假设得到的测量结果非常不准确.
近些年国内外的研究虽取得了一定的成果,但主要集中在使用电涡流传感器对曲面零件探伤和测厚方面,如重要结构件探伤、检测管道等零件涂层厚度.Thompson[4]采用脉冲涡流法定量检测多层结构内部的腐蚀问题.Mitra等[5]提出采用多频涡流检测技术开展飞机部件搭接结构中的缺陷成像研究.曾亮[6]利用涡流法检测特种碳纤维复合材料绝缘涂层,测得的有效测量范围约为30~800 μm,测量精度绝对值约为 20~30 μm.姜磊等[7]使用电涡流法测试应力作用下碳纤维复合材料的位移,获得应力水平对传感器灵敏度的影响规律.
针对电涡流位移传感器的曲面位移测量问题,目前的相关研究较少.胡鹏[8]基于涂镀层厚度检测问题,研究以平板标定结果测量曲面零件表面涂镀层厚度,研究结果表明该方法检测误差大,完全不具有实际应用价值.李德维等[9]设计了一种基于电涡流位移传感器的车轮形状测量方法,得到传感器对正曲率与负曲率曲面实测值与标定值的误差分析结果,但只概括性地给出曲面几何形状对电涡流位移测量输出特性影响规律的定性分析.由于没有建立数学模型,无法进一步定量分析涡流位移传感器的测量误差.高宽厚等[10]提出一种双层导电涂层厚度的电磁无损检测方法,厚度检测误差低于10%,但其理论推导和试验验证都是针对平面零件的.
基于上述问题,本文以燃料贮箱筒段外表面聚氨酯泡沫层的厚度测量为例,开展4种常见筒段试件标定试验.由于聚氨酯泡沫不导磁、不对磁场产生影响,试验对象采用未喷涂聚氨酯泡沫的曲面试件,标定试验过程中将厚度测量转化为距离测量.提出基于支持向量机回归的标定方法,以上述标定数据为样本建立提离距离预测模型(LDPM).需要注意的是,标定试验流程通过涡流位移传感器逐步向上提离试件表面以模拟不同厚度的泡沫层,因此被称为提离距离预测模型.研究曲率对涡流测距测量误差的影响规律,按误差产生的原因可以将测量误差分为两部分:表面曲率误差和其他误差.分析各部分误差在传感器量程范围内的分布规律,为曲面零件涡流测距误差补偿提供参考依据.此外,对比分析LDPM与4次多项式拟合和5项Gaussian函数[11]拟合两种常用标定方法在测量精度、计算速率方面的优劣,为曲面零件涡流测距选用何种标定方法提供建议.
1 试验方案
1.1 试验设置
根据燃料贮箱筒段外表面聚氨酯泡沫层厚度的测量要求:常用筒段曲率范围为0~0.9/m,传感器量程范围内的测量误差控制在 ±0.5 mm以内.选取4种典型尺寸的曲面被测试件:曲率半径分别为1.125 m(N1)、1.675 m(N2)、3.000 m(N3)以及平面(N4),材料均为铝合金6 063,表面粗糙度Ra=6.4 μm.
试验系统主要分为测量模块与数据采集模块.测量模块包括电涡流位移传感器、被测曲面试件、传感器固定夹具、高精度机床;数据采集模块包括数据采集卡和数据显示屏幕.通过夹具将电涡流传感器探头固定于高精度机床主轴,机床主轴移动改变提离距离,数据采集卡实时采集传感器的输出电流信号,并由PC上位机显示和保存.试验系统的总体结构如图1所示.传感器选用的是上海冉普电子科技有限公司生产的RP6660电涡流位移传感器,其性能参数如表1所示.

表1 电涡流传感器技术指标Tab.1 Technical indicators of eddy current sensor
整体测量位于美国赫克公司生产的HURCO VMX42五轴立式加工中心,机床参数如表2所示.
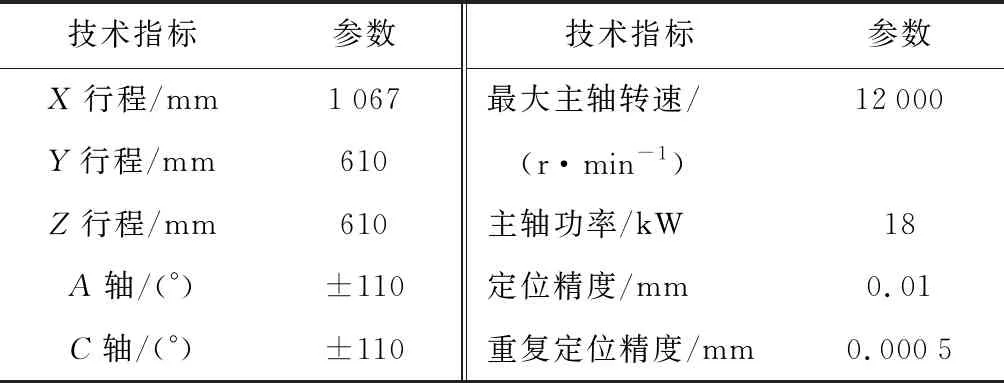
表2 机床性能参数Tab.2 Machine tool performance parameters
使用USB5001数据采集卡实时釆集传感器输出的电流信号I,如图2所示.其中:t为采集时间;采样频率设为1 kHz.
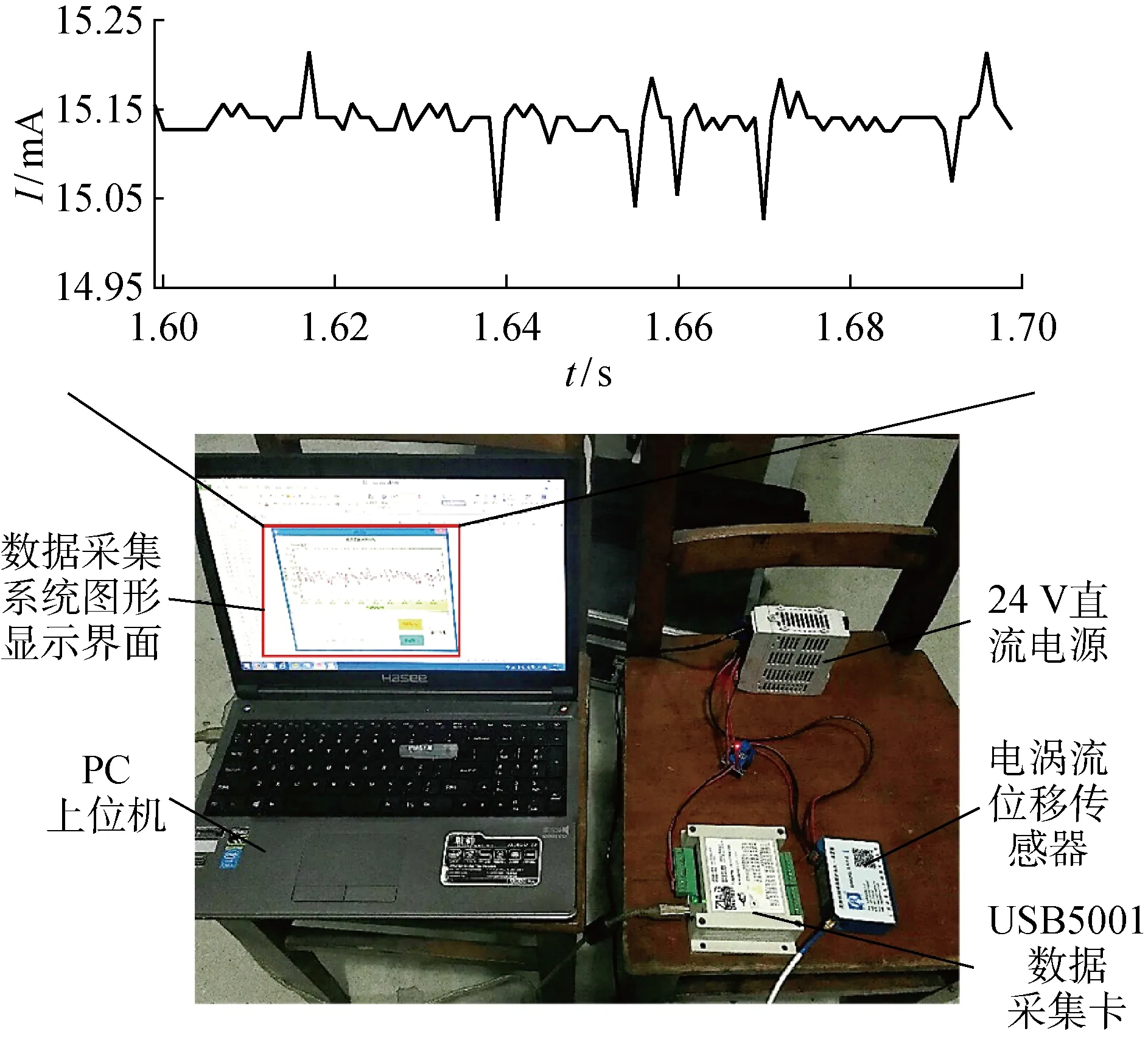
图2 数据采集模块Fig.2 Data acquisition module
试验现场设置如图3所示,将传感器探头通过夹具夹持并固定于机床主轴, 确保探头位于被测试件正上方且探头轴线沿试件曲面法线方向.传感器探头与被测试件需严格按照图3的位置关系安装定位,否则定位误差会导致极大的测量误差,使标定数据不可靠.
1.2 试验方案
首先确定测量起始位置,手动控制机床主轴沿Z轴移动至量程范围内锁住主轴Z向,主轴沿Y向以最小进给量缓慢移动,找到传感器示数最小的Y向位置,锁住主轴X、Y向,使主轴以最小进给量沿Z轴缓慢接近被测试件表面.当0.03 mm的塞尺刚好不能塞入探头与试件表面间的缝隙时,停止进给,将提离距离0.03 mm作为起始位置.在传感器量程范围内,每隔0.5 mm改变一次提离距离,将传感器输出电流信号和提离距离作为标定数据样本点.为减少测量误差,每个提离距离截取1 s稳定测量阶段的信号数据(即 1 000 个数据点),对输出电流波形滤波去噪,然后取平均值,即为该提离距离对应的涡流信号.为减少随机误差,每种曲面试件从起始位置到量程终点每个位置按上述操作重复测量5次取平均值.需要注意的是,每次更换曲面测试件后都需要对传感器探头重新找正与定位.
1.3 数据预处理
对试验获得的涡流信号预处理,如滤波去噪、取均值等.以提离距离y=20.53 mm为例,使用移动平均滤波器对信号进行平滑处理,窗宽为30个样本点,滤波结果如图4所示.电流信号平均值为15.3 mA时代表y=20.53 mm,两者构成数据集中的一个样本点.以此类推,可以获得传感器量程范围内,每个提离距离所对应的电流信号.

图4 电流信号的平滑滤波Fig.4 Smoothed and filtered current signal
2 基于支持向量机回归的标定方法
支持向量机回归(SVR)是高效的监督学习方法,能够兼顾模型的复杂性和学习能力、最小化经验误差和最大化几何边缘,在解决小样本、非线性及高维模式识别中表现出独特的优势[12].
训练数据可表示为
{xi,yi},i=1,2,…,n,yi⊂R,xi⊂RD
(1)
式中:xi为数据样本特征,对应曲率和涡流信号;yi为数据样本标记,对应提离距离;D为数据维度,此处D=2;n为样本数,此处n=490.
对于非线性的SVR问题,可以通过映射函数φ(·),将输入数据映射到高维特征空间F中[13]
f(x)=w·φ(x)+b
(2)
式中:w为权重向量;b为常数;f(x)为回归预测模型输出,其与yi之间存在一定的误差,可通过损失函数来评价模型预测的好坏[14].需要解决的优化问题可用下式表示
(3)
|y-f(x)|ε=max{0,|y-f(x)|-ε}
(4)
(5)
式(5)即为最终的标定函数表达式,其中k(xi,x)为核函数.
本文以曲面试件N1、N2、N3、N4标定试验数据为样本,基于SVR的标定方法,建立LDPM.对于常见曲率范围0~0.9/m,LDPM的输出结果如图5所示,其中κ为曲率.由图5可知,提离距离随电流信号的上升而增加.在传感器量程初始阶段,等高线沿着曲率轴方向波动,在I=4 mA处达到最大,与最小提离距离相差3 mm;当I=15.5 mA时,等高线基本和曲率轴平行,曲率和提离距离的相关性并不明显;在传感器量程终点区域,等高线从左上角往右下角倾斜,说明涡流位移传感器在相同的提离距离下,曲面零件曲率越大,输出的电流信号越小,即传感器的最大提离距离与曲率呈正相关,曲率越大,传感器的最大提离距离越高.
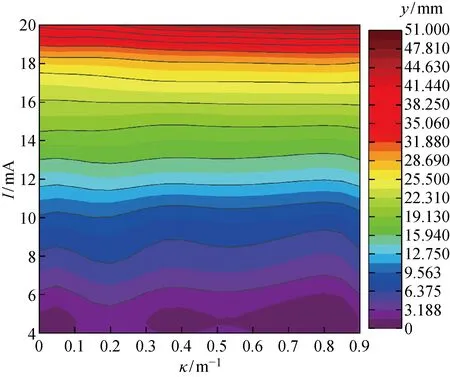
图5 基于支持向量机回归的提离距离预测模型Fig.5 Lifting distance prediction model based on support vector machine regression
下面研究LDPM在N1、N2、N3、N4上的测量误差,定量分析曲率对测量误差以及误差分量的影响规律.
(1) 对于同一曲率,LDPM的测量误差Δy与y的关系基本呈三角函数关系变化,如图6所示.对于精度要求较高的应用场合,选取误差曲线与Δy=0相交处的y作为关键位置.曲面试件N1、N2、N3的测量误差曲线与平面试件N4的误差曲线差异明显,因此将平板标定的结论用于曲面零件涡流测距会产生较大的测量误差.

图6 Δy随y和κ的变化规律Fig.6 Δy versus y and κ
(2) 将测量误差按产生的原因分为两类:受被测试件表面的曲率影响产生的测量误差值简称表面曲率误差Δyκ;其他误差Δyo包括温度漂移、机床定位误差、数据采集卡A/D转换误差以及标定过程中电涡流探头安装定位误差.表面曲率误差和其他误差在传感器量程范围内的分布如图7所示.其中,其他误差为LDPM在N4上的测量误差;N1、N2、N3的表面曲率误差等于测量误差减去其他误差.表面曲率误差和其他误差在整个传感器量程范围内交替变化,分布在Δy=0两侧且呈现出相互抵消的趋势,N1、N2、N3的表面曲率误差曲线近似为多个周期和幅值不同的余弦函数拼接而成.在传感器量程起点区域a内,N1、N2、N3的表面曲率误差曲线为单周期的余弦函数且幅值较小,其他误差占主导,3种曲面试件的测量误差曲线重和性较好,如图6所示;而在区域b内,N1、N2、N3的表面曲率误差曲线幅值和周期均有所增大,此时其他误差维持在最大值附近,3种曲面试件的测量误差位于Δy=0上方;在测量中点附近区域c,N1、N2、N3的表面曲率误差达到最大值,其他误差近似于正弦函数,误差相互抵消;在终点区域d,N1、N2、N3的表面曲率误差幅值接近为其他误差的1.5倍,超过其他误差占主导地位.

图7 Δyκ及Δyo的分布Fig.7 Distribution of Δyκ and Δyo
(3) 研究曲率对表面曲率误差的影响规律.不同区域a、b、c、d处,表面曲率误差随着曲率的变化规律会有所区别,如图7所示.在传感器量程起点区域a内,表面曲率误差曲线重合,表面曲率误差与提离距离的变化趋势相同,对曲率不敏感;在区域b内,N1、N2的表面曲率误差曲线基本重合,但N3的表面曲率误差曲线始终位于其下方,具体表现为相同的提离距离,表面曲率误差绝对值随着曲率的增加而减小;在测量中点附近区域c,3种曲面试件的表面曲率误差曲线在大部分位置重合,但在峰谷等位置处差异明显,具体表现为相同的提离距离,表面曲率误差绝对值随着曲率的增加,先减小后上升;在终点区域d,表面曲率误差绝对值随着曲率的增加而上升.
在量程范围内通过补偿其他误差来减小测量误差,具体通过分析误差分量正负号的变化规律,为曲面测量误差补偿提供依据:当正负号相反时,两者的综合效果会使总测量误差下降,此时停止补偿其他误差;当正负号相同时,以通过补偿其他误差的方法来减小测量误差.以N1为例,误差补偿前后测量误差的变化如图8所示,补偿之后的误差曲线更接近Δy=0.
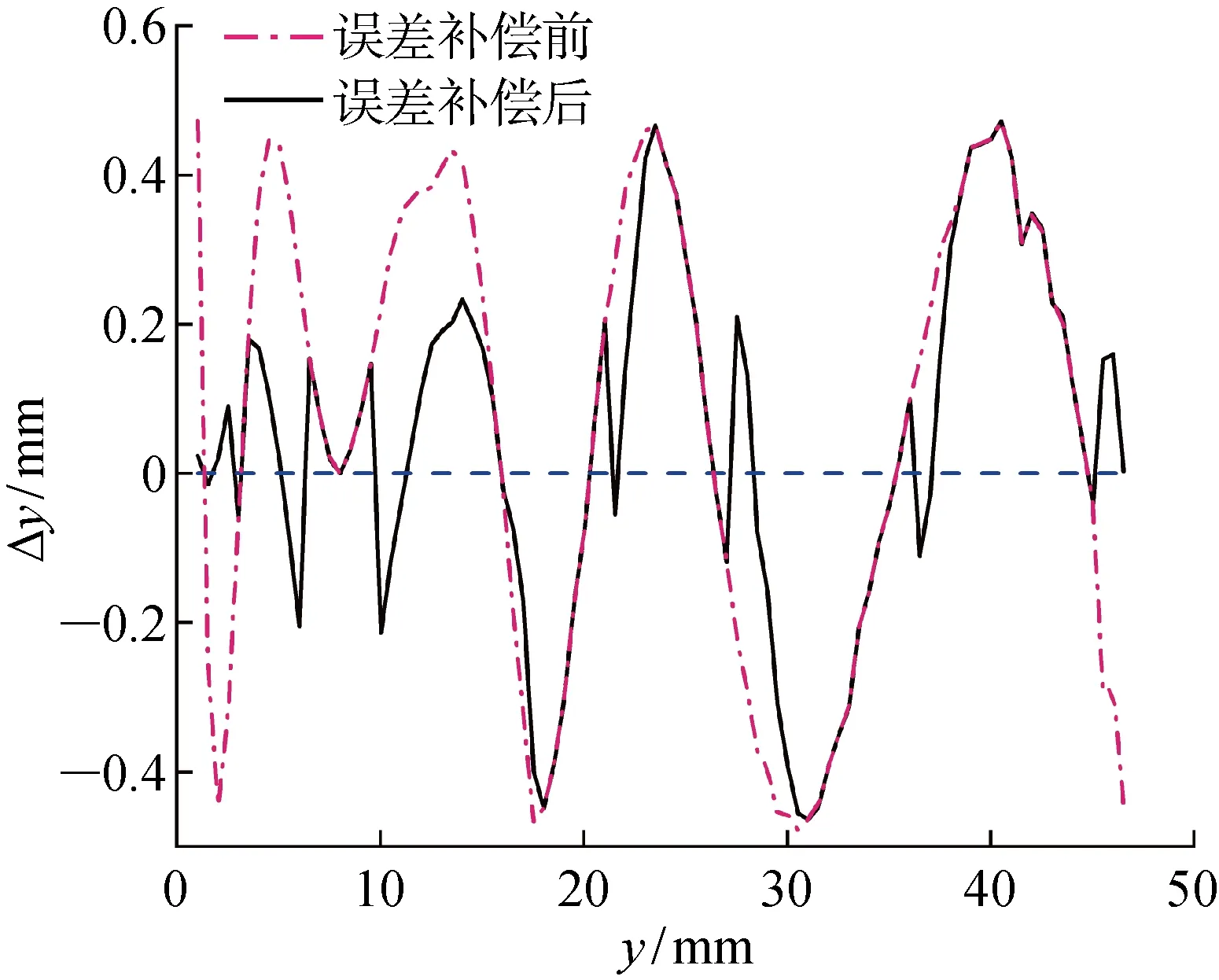
图8 误差补偿前后模型的Δy变化Fig.8 Variation of Δy before and after error compensation
使用误差平方和(SSE)来衡量预测值与样本点的接近程度,SSE越接近于0,LDPM的精度越高.
(6)
式中:pi表示分布率,此处取为1;fi表示样本点i处的标定结果,yi表示样本点i处的真实提离距离.N1、N2、N3误差补偿前的误差平方和SSEbe与误差补偿后的误差平方和SSEaf,以及补偿前的最大误差绝对值MAEbe和补偿后的最大误差绝对值MAEaf的对比如表3所示,其中σ为下降量.对于N1、N2、N3,误差补偿前后的SSE分别下降了41.5%、43.6%以及41.4%;MAE下降了1.1%、2.5%以及3.2%,LDPM的输出结果更接近真实提离距离.

表3 N1、N2、N3误差补偿前后预测效果比较
3 LDPM与典型标定方法的比较
在实际应用过程中,针对曲率范围内常用的几种曲率试件做标定试验,将得到的LDPM用于涡流测距系统的标定函数.而典型标定方法如多项式拟合、多峰Gaussian拟合标定,也常用于确定标定函数.不同之处在于,LDPM可适用于整个常用的曲率范围,而常用标定方法确定的标定函数参数只针对特定曲率有效,对于不同的曲率需要重新标定更新参数.下面针对N1,对比分析LDPM、4次多项式拟合(Poly4)以及5项多峰Gaussian函数拟合(Gauss5)[11],以SSE、均方根(RMSE)为评价指标,对比分析不同的标定方法.
均方根表示样本数据点相对于标定曲线的离散程度[16],

(7)
LDPM和不同标定方法的误差对比如图9所示,LDPM与4次多项式拟合和5项多峰Gaussian函数拟合的误差统计分析如表4所示.其中η为预测误差下降量.
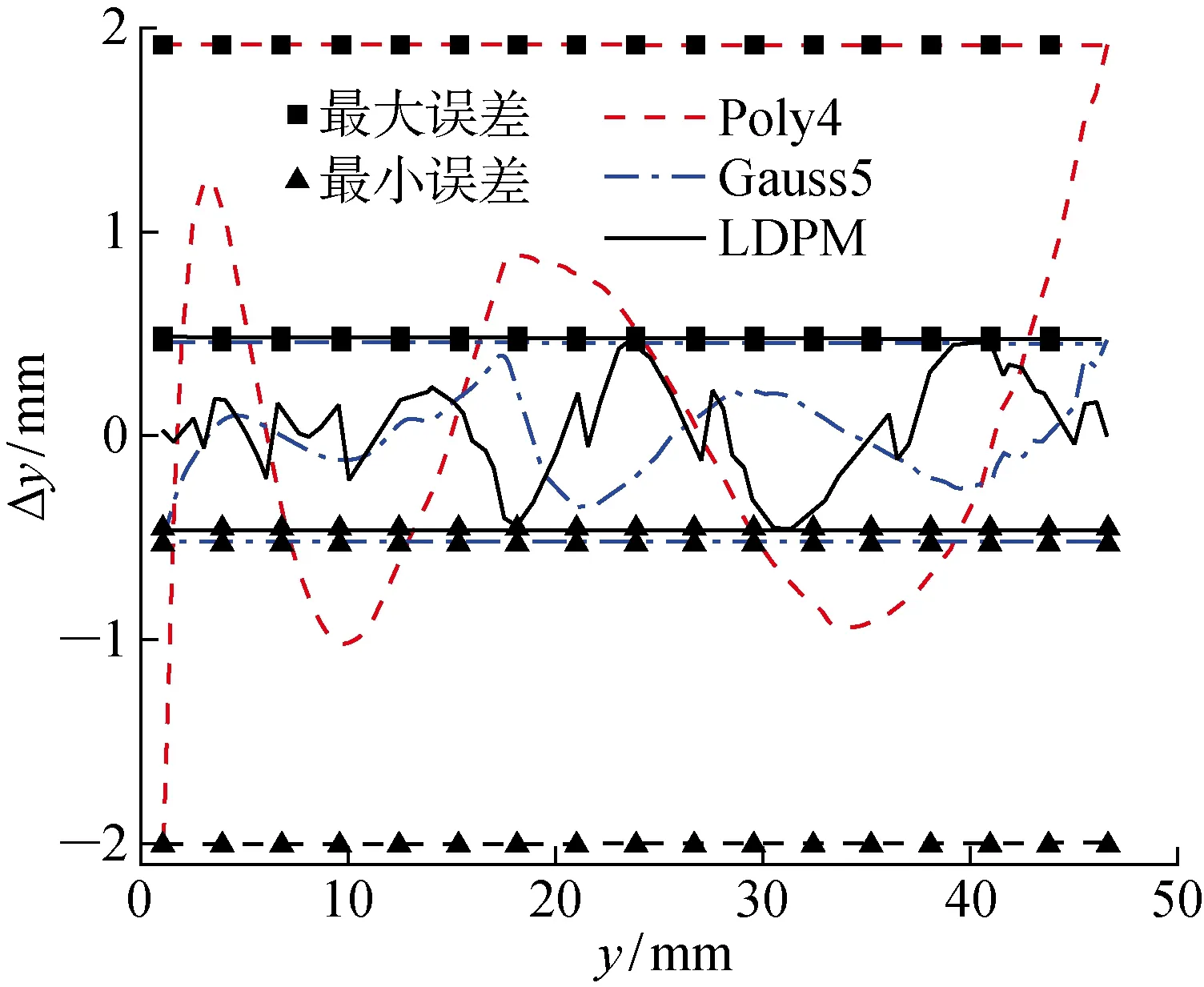
图9 LDPM与不同标定方法的误差对比Fig.9 Error comparison among LDPM and other methods
由表4可知,LDPM测量精度高于4次多项式拟合,相比较而言,SSE下降了90.4%,RMSE下降了69.0%以及MAE下降了76.3%.与5项多峰高斯拟合相比,SSE下降0.4%,RMSE下降0.2%以及MAE下降8.4%,两者的测量精度相当.

表4 不同标定方法的误差统计分析Tab.4 Statistical analysis of errors for different calibration methods
此外,运算速度也是选择何种标定方法的一个重要指标,不同标定方法因计算复杂程度不一,运算速率也有差异,比较上述3种方法平均单点运算时间.随机取100个测试电流的数据,使用MATLAB中的tic和toc函数得到总运行时间进而获得单点运算时间,运行环境为Windows10、MATLAB R2016b,运算结果为:Poly4的运算时间为0.542 s;Gauss5的运算时间为1.178 s;LDPM的运算时间为2.452 s.
LDPM与4次多项式和5项Gaussian函数拟合相比,单点运算时间是4次多项式拟合的4.52倍,是5项Gaussian函数标定方法的2.08倍.适用于采样频率不超过407 Hz、测量精度高的应用场合.当然,上述比较结果只是提供了相对的大小关系,涡流测距系统的最终采样频率还要考虑其他因素的影响,包括数据采集模块的数据处理能力、通信方式的选择等.
4 结论
本文分别针对曲率半径为1.250、1.675、3.000 m曲面试件以及平面试件进行标定试验,提出基于SVR的标定方法,建立LDPM用于曲面零件的涡流测距,分析测量误差分量的分布规律,提供误差补偿策略,并与常用的标定方法在测量精度、运算速率等方面进行比较,结论如下:
(1) 针对曲面零件涡流测距,LDPM的输入为测量电流信号值(4~20 mA)、被测试件的曲率(0~0.9/m),输出是距离值.针对该型号的电涡流位移传感器,LDPM的误差可以控制在[-0.5, 0.5] mm,精度与5项多峰Gauss拟合相当,高于4次多项式拟合,能够满足一般应用场合需要,简化了标定流程,具有重要的应用价值.
(2) 根据误差产生的原因将测量误差分为两部分:表面曲率误差和其他误差.LDPM在传感器量程初始阶段0~5 mm,表面曲率误差曲线重和性较好,曲率对表面曲率误差影响不敏感;在范围5~16 mm,表现为在提离距离相同时,表面曲率误差绝对值随着曲率的增加而减小;在测量中点附近区域16~28 mm,误差曲线在大部分位置重合,但在峰谷等位置处差异明显,具体表现为相同的提离距离,表面曲率误差绝对值随着曲率的增加,先减小后上升;在终点区域,表面曲率误差绝对值随着曲率的增加而上升.
(3) 在整个量程范围内的不同测量区间,其他误差保持不变,可以通过补偿其他误差来减少测量误差,分析两个误差分量的相对大小变化规律,为曲面测量误差补偿提供依据:当处于其他误差和表面曲率误差的正负号相反的测量区间时,两者的综合效果会使总误差减小,此时停止补偿其他误差;当处于其他误差和表面曲率误差的正负号相同的测量区间时,此时可以通过补偿其他误差的方法来降低总误差.
(4) LDPM的单点运算时间约为2.45 ms,是4次多项式拟合的4.52倍,限制了涡流测距系统的最终采样频率.因此,在实际应用过程中需要结合不同应用场合的采样频率需求判断该方法是否合适.

