基于RBF-AR的船舶变形极短期预报
高健钦,彭侠夫
(厦门大学 航空航天学院,福建 厦门 361100)
0 引言
随着我国军事武器装备作战性能的不断提升,舰船在航行过程中产生的角形变已成为提升武器装备作战性能的瓶颈。大型舰船如导弹驱逐舰、航母等舰船并非刚体,在运动过程中会产生角形变[1]。舰船角形变产生的主要原因有以下几点:一方面是由于载荷变化使得重力分布产生变化引起的形变,另一方面温度变化也会导致船体结构出现缓慢的变化,此外舰船在航行过程中受到的海浪冲击、武器发射时产生的冲击等作用也会引起船体的形变[2]。船舶角形变可根据产生原因和数量级差异,分为静态角形变和动态角形变。形变幅值高达1°~5°,且短时间内几乎不随时间变化,为静态形变。形变幅值约为几十角秒,随时间变化较快,为动态形变。根据Wei Wu[3-4]的研究内容分别从伯努利-欧拉梁理论和先前实测数据特征分析证实动态角形变符合二阶马尔可夫分布。船体变形角的存在是制约大型舰船建立统一空间基准的根本原因,直接影响舰载装备精度,因此对船舶变形进行极短期预报研究具有重要的意义。
船舶变形极短期预报是指利用船舶变形以及其他海况等的测量数据对船舶变形规律建立模型并预报未来五秒到十秒钟的变形角大小,以便更好地提前做出控制策略[5]。关于对船舶运动及变形极短期预报的研究,国外最早开始于20世纪70年代。最初,极短期预报采用的方法计算繁杂,难以实际开展。20世纪80年代以后,现代控制理论发展成熟,在线实时预报与控制得以实现,预报工作进入可行性研究阶段。目前,基于不同的原理,已相继提出了多种船体变形预报方法。船体变形预报方法大致可以分为试验方法和理论方法两个方面,现阶段对舰船角形变的极短期预报方法主要是孙佳丽等采用基于有限元分析技术[6]或黄强等采用基于船体梁弹性变形的理论计算为主[7]。试验方法由于比较依赖形变模型及参数准确程度,因此未得到广泛的应用。时间序列分析方法通常是按时间顺序排列的一系列被观测数据,按固定时间间隔对观测数据进行采样。在用此方法作预测时,常以过去的历史资料为依据,寻找观测数据序列的规律,预测将来的变化。由于舰船的变形具有很强的随机性和非线性,使用传统时间序列分析的方法进行预报并不能获得理想的效果。
近些年来,神经网络因其非线性映射、自学习、自适应等特点,已经成为一种流行的系统建模和时间序列预测工具。RBF神经网络作为一种高效的前馈式神经网络,具有独特优势。相较于BP神经网络,RBF神经网络收敛速度更快,其最佳逼近性能也更便于得到全局最优解[8]。其中,RBF神经网络由于其结构简单、非线性逼近精度优和学习速度快等特点得到了广泛青睐。在20世纪90年代,就先后有学者利用RBF网络来逼近SD-AR模型中的函数系数[9-10]。然而由于对模型参数准确性过分依赖,早期建立的RBF预测模型虽能达到预测大致趋势的效果,但因其模型具有较强的随机性,始终无法应用于工程项目之中。
目前,将RBF神经网络应用于船舶变形的相关研究较少。应用RBF-AR模型进行船舶变形极短期预报的难点在于模型参数的辨识,包括模型阶次、RBF网络中心的选取以及线性权重等。甘敏等[11]提出了两种用于RBF神经网络参数估计的混合算法,其中SNPOM辨识方法收敛速度快,精度高,优于现有其他算法。本文使用径向基神经网络建立船舶变形模型并采用SNPOM辨识方法,克服了RBF网络预测随机性的问题,能有效减少训练时间并提高预报精度。并结合符合挠曲变形特征的仿真数据对提出方法的可行性与有效性进行了验证。
1 船体变形预报模型
针对船舶角形变的非线性特征,对于一个确定的时间序列{y(t)∈R1,t=1,…,N},非线性时间序列建模主要任务是构建如下映射关系,f:Rp→R1,可表示为:
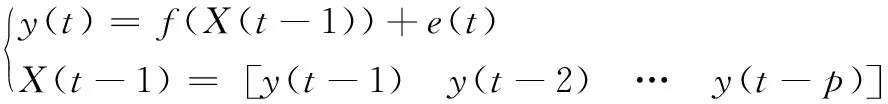
(1)
式中,y(t)∈R为预测输出值,f(·)为非线性映射,e(t)为高斯白噪声,X(t-1)为t时刻的状态向量,p为模型阶次。
式(1)为一般表达形式,不能直接应用。在实际控制中,通常采用状态相依自回归模型[12],其结构特征如下:
(2)
式中,{φi(X(t-1)),i=1,2,…,p}为状态相依函数系数。
RBF网络可以任意精度逼近任何函数,因此可用于逼近模型(2)中系数。高斯RBF网络的结构如图1所示。

图1 RBF网络结构
根据图1所示结构,RBF神经网络是前馈神经网络,输入向量和输出向量的函数关系通过非线性映射表现出来。其结构可分为三层,包括输入层、隐含层和输出层。第一层是输入层,由信号源节点组成。第二层为隐含层,其输出由输入矢量与径向基函数中心之间的距离确定,中心函数一般选择高斯函数。第三层是输出层,表现为隐含层的输出到输出层的线性映射。
高斯RBF神经网络可以表示为:
(3)
式中,w0为偏置,{wi,i=0,1,…,m}为隐含层到输出层的权重,m为隐含层节点数,λk表示RBF网络的比例缩放因子,X为输入向量,Z为中心向量,‖·‖为欧几里得范数,表示向量的欧氏距离。
用式(3)所示RBF网络逼近式(2)中状态相依函数系数,得到RBF-AR模型结构如下:
式中,{wik,i=0,1,…,p;k=0,1,…,m}为线性权重,d为模型的阶次。
由此可以看出,RBF网络是RBF-AR模型的一个组成部分,因此RBF-AR模型更具普适性。一般情况下,式(4)中不同回归部分具有不同中心值,即使RBF网络中心相同,其回归多项式系数也可能不同。因此,在达到相同精度条件下,RBF-AR模型可能拥有更少的中心值。为了简化计算,本文采用相同中心值与不同回归多项式系数。
2 变形预报模型参数辨识
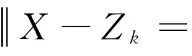
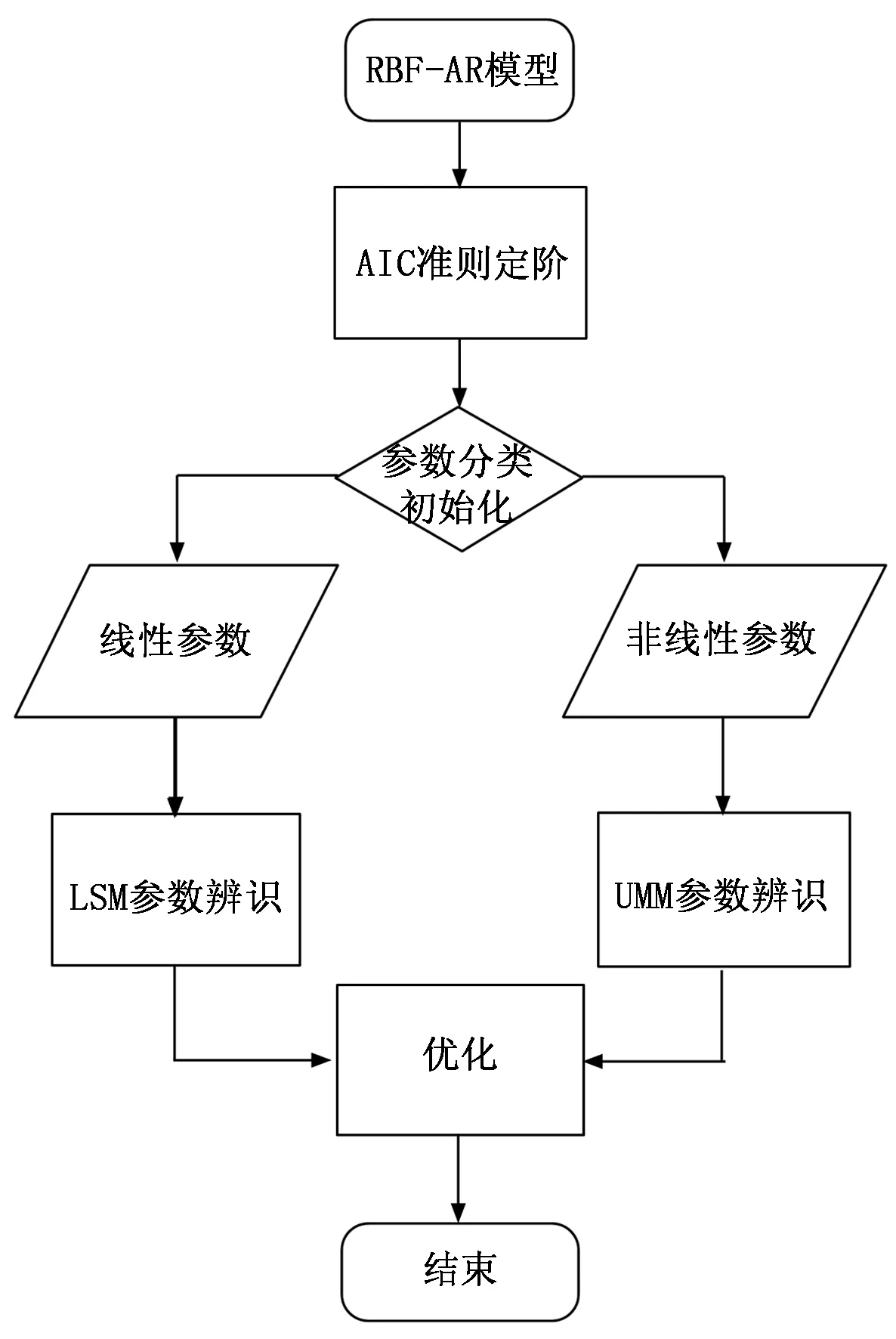
图2 模型参数辨识流程
2.1 模型定阶
对于船舶角形变预测模型阶次的选择,采用高AIC准则进行定阶,AIC值越大表示阶次更为合适,计算过程如下:
(5)
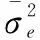
2.2 参数分类
RBF-AR的模型(4)参数分为线性参数和非线性参数,其中线性参数可表示为:
θL={w0,wik|i=0,1,…,p;k=0,1,…,m}∈R(m+1)(p+1)
(6)
非线性参数主要是网络中心及宽度,可表示为:
θN={λk,Zk|k=0,1,…,m}∈Rm+d
(7)
将式(4)进行化简可得:
y(t)=f(θL,θN,X(t-1))+e(t)
(8)
y(t)=Ψ(θN,X(t-1))TθL+e(t)
(9)
2.3 参数初始化

(10)
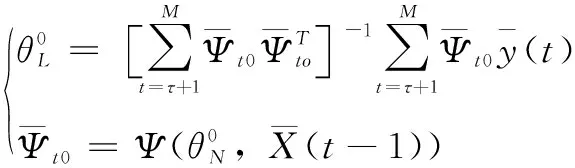
(11)
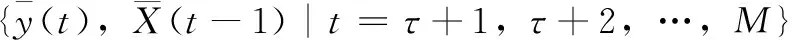
2.4 优化过程
定义残差的平方和作为目标函数:
(12)
(13)
因此,该优化问题可以转换为求:
(14)
根据式(11)可推得线性参数θL和非线性参数θN的更新公式为:
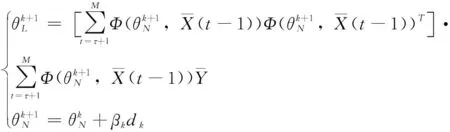
(15)
式中,k为迭代步数,βk为搜索步长,dk为搜索方向。dk的值难以直接求解,因此引入雅克比(Jacobian)矩阵,形式如下:
(16)
因此,可通过下式求出dk值:
(17)
式中,γk决定了dk的幅度和方向,如果下降太快,使用较小的γk,使之更接近高斯牛顿法 ;如果下降太慢,使用较大的γk,使之更接近梯度下降法[14]。

3 仿真验证
为验证所提变形预报方法对船舶角形变序列的跟踪能力,设置了一组仿真实验,通过模拟产生符合角形变特征的仿真数据,采用RBF-AR预报算法与传统AR预报模型进行计算并比较其跟踪能力。
船体甲板基准坐标系的坐标原点一般选定在艏艉线的中部,舰载设备沿艏艉线呈纵向分布。船体坐标系定义为oxyz,oy沿着船体的纵轴指向船艏,oz垂直于甲板平面指向上方,ox指向船体右舷,与oy、oz构成直角坐标系,即右前上坐标系。定义ox方向的变形为纵挠角(pitch),oy方向的变形为横扭角(rolling),oz方向的变形为艏挠角(heading)。
文中所建立的是极短期的预报模型,因此静态角形变可以视为常数[15],采用的仿真数据为服从二阶马尔科夫过程分布的动态角形变与为常值的静态角形变叠加而成的总形变角序列。船体强度理论研究和实际实验表明,对于有限时间间隔来说,船体动态形变可视为平稳随机过程,即数学期望和相关函数不变。因此,动态形变角由以下公式仿真获得:
(18)
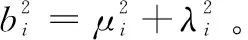
根据表1参数的设置,船体变形角仿真数据如图3所示。
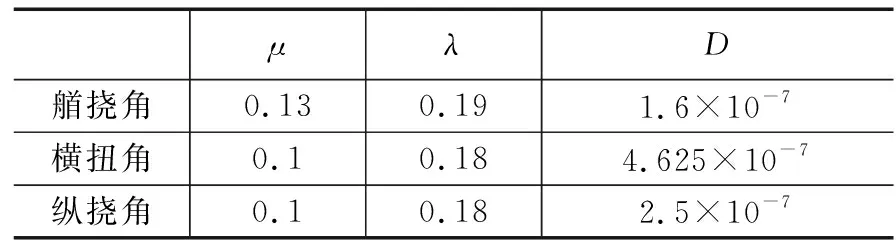
表1 动态角形变参数设置
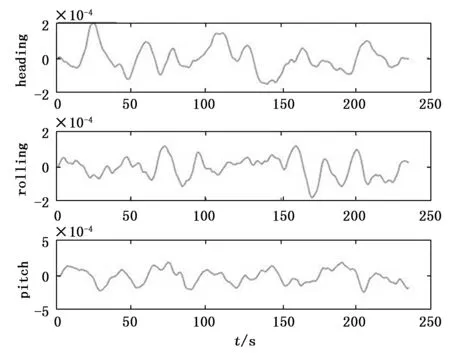
图3 三轴的仿真变形角
图3所示为仿真环境中三轴角形变大小,从上至下分别为艏挠角、横扭角、俯挠角,通过图片可以观察到,三轴的变形角曲线都具有一定的随机性。对数据进行截取,取0~180 s的船体变形角数据进行训练和辨识,180~235 s的数据进行预报对比,通过对三轴角形变仿真数据的预报来验证RBF-AR模型的有效性。采用均方误差(mean squared error,MSE)来评价预测精度:
(19)
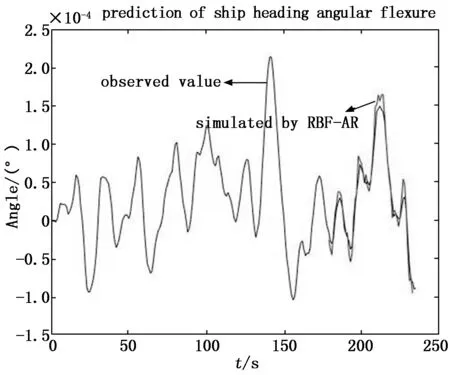
图4 艏挠角RBF-AR预报结果
为公平比较及说明RBF-AR模型的预测精度,分别采用两种船体变形极短期预报方法,在同一组变形仿真数据上测试两种预报方法的性能。图4~图9分别为船体变形艏挠角、横扭角、纵挠角两种方法的变形预报曲线,从图中可以看出两种方法都能够大致跟随船体角形变的变化趋势。从图4与图5,图6与图7,图8与图9的预报结果比较可以看出改进的算法提高了预报精度,大大减小了变形幅值预报误差。由此可得,RBF-AR模型具有较强的跟踪能力,能够有效、准确地对船舶角形变进行预报。与此同时我们也能通过图4、图6、图8的预报曲线观察到,对于船舶变形预报序列而言,同阶的非线性自回归模型比线性回归模型有更高的精度,但在最大幅值处的预测仍存在一定误差。
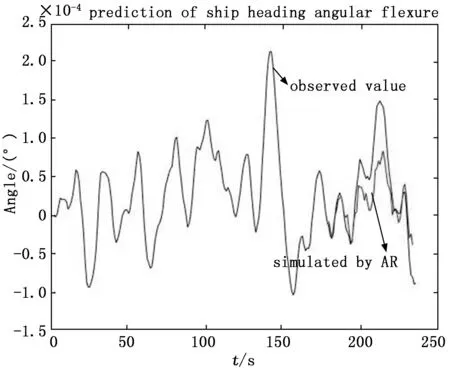
图5 艏挠角AR预报结果

图6 横扭角RBF-AR预报结果
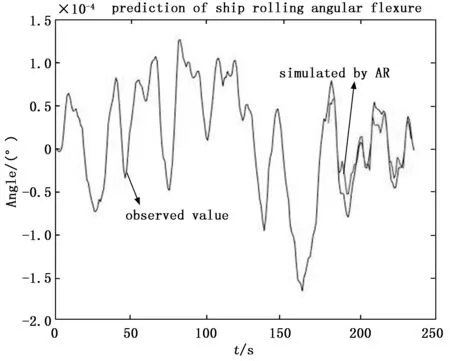
图7 横扭角AR预报结果
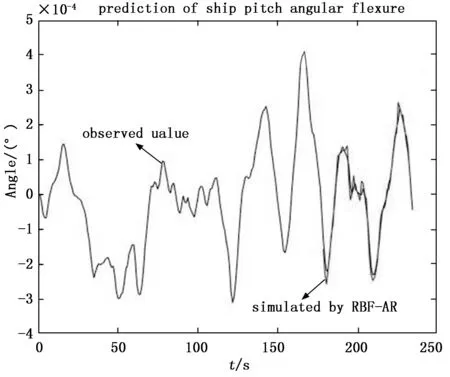
图8 纵挠角RBF-AR预报结果
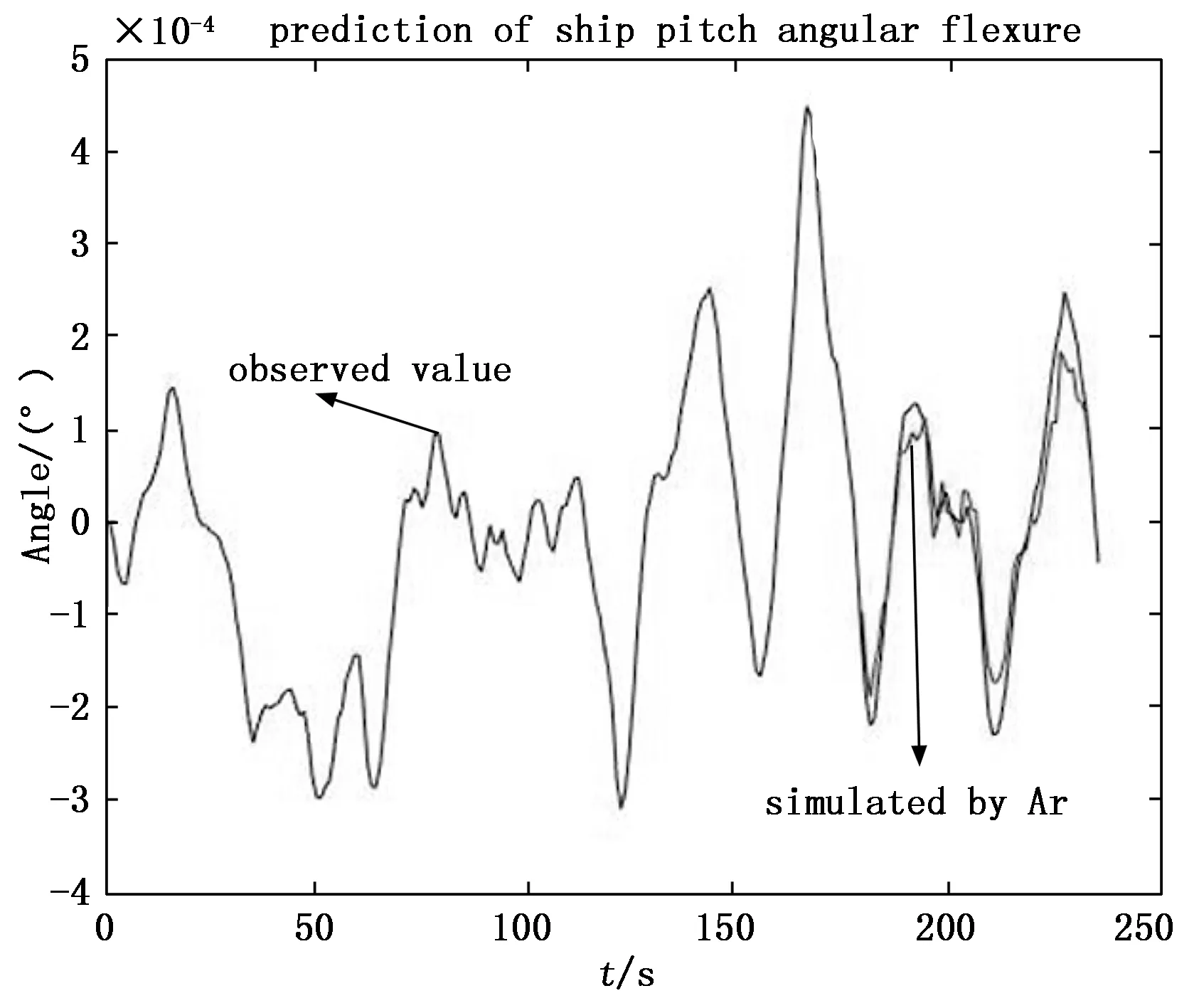
图9 纵挠角AR预报结果
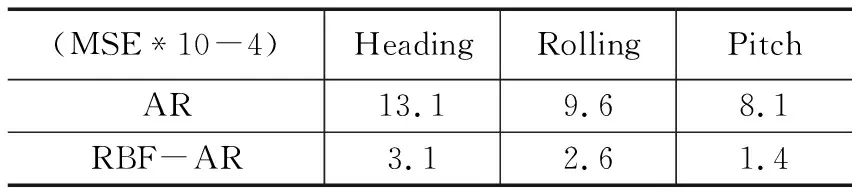
表2 预报性能指标
通过表2给出了两种预报方法的均方误差(MSE),通过对比两种预报方法的均方误差值也可以验证改进算法对于预报效果的提升。
综上所述,文中提出的RBF极短期船体变形角预报算法是有效的,能取得比较好的效果。
4 小结
本文针对传统AR模型难以预测船体角形变的问题,在AR预报模型的基础上提出了一种用一组RBF神经网络逼近AR-SD模型参数的预报模型,从而可在全局范围内搜索最优解。算法分析与实验结果表明:传统的时间序列预测方法无法实现对变形角的跟踪,预测模型误差较大。RBF-AR模型相较于传统的时间序列模型具有跟踪效果好、计算过程少的优点,对预报过程中船体变形随机性、非线性的问题,具有较好的预报效果。在Matlab中使用自带函数拟合模型时,模型存在较强的随机性。而使用结构化的非线性参数优化方法(SNPOM),不仅有效的解决了线性参数与非线性参数互相混杂、难以辨识的问题,而且也使模型具有确定的参数。
5 结束语
对船体角形变进行精准预报,实现全舰统一姿态基准是舰载武器装备系统协同工作的重要前提。RBF-AR模型在船体角形变预报任务中具有非常好的应用前景。在实际应用中可以节省大量的计算量和时间成本,极大地提升预报效果,对建立全舰统一姿态基准提供巨大帮助。在未来的工作中,会将算法结合实测数据已经半物理仿真平台中进行试验,提升算法的适用性,对船体变形精确预报,推动实现各站位点姿态基准的精确引射和统一。

