物理中的隐性知识的作用和价值

徐建涛

知识可以分为显性知识和隐性知识两种。能够以书面文字、图表和数学公式加以表述的，称为显性知识;而未被表述的知识，比如在做某事的行动中所拥有的知识，称为隐性知识。如果把显性知识比喻成材料，那么隐性知识就是方案、方法、工具。在物理学科中“做某事的行动”可以是解决物理问题或是做物理实验。本文研究的是在解决物理问题中所体现的隐性知识，包括观点判定、思维建立、方法选择、模型比较等，它们难以以文字的形式表述出来，却对问题的解决不可或缺。显性知识与隐性知识的学习如影随形。学习概念、规律、定理等显性知识离不开对其中蕴含的隐性知识的理解。例如：“质点”是有质量的点，是显性知识。但是，它是从具体物体中抽象出的，这种复杂问题的简单化，就是形式层面的隐性知识;突出主要因素，忽略次要因素，就是方法层面的隐性知识。学生反映高中物理难学，原因主要在于没有很好地理解和掌握隐性知识。

例如：高为h且足够长的木板质量为M，最初静止在光滑地面上，质量为m的小木块以初速度v₀从左端冲上长木板。长木板的上表面粗糙，木板与木块间的动摩擦因数为μ，小木块最终与木板以相同的速度一起向右运动。从刚冲上木板到最终共速的过程中，求解以下问题。问题A：木块和木板各自的加速度？问题B：木块与木板共速时的速度是多少？问题C：木块对地面的位移是多少？问题D：木板对地面的位移是多少？问题E：木块和木板组成的系统产生的热量是多少？问题F：木块在木板上滑行的时间是多少？问题G：木塊受到怎样的冲量？问题H：木板受到怎样的冲量？

该习题从内容来看，既涉及时间量，又涉及空间量;从分析角度来看，有力和运动、功和能量，动量和冲量三种观点可供选择;从解题过程来看，既涉及科学思维的建立，又涉及科学方法的选择。让学生在准确应用显性知识的同时深刻体会隐性知识的作用和价值。

一、隐性知识在运用解题观点中的作用和价值

“板块模型”可以“一题多问”。题目中提供的已知条件不同、所求物理量不同，学生选择的分析观点也就不同。从条件出发，利用小木块的质量和动摩擦因数可以求出二者之间的滑动摩擦力。解决问题A只能使用力和运动的观点。解决问题B既可以使用力和运动的观点，又可以使用动量和冲量观点。解决问题C、D、E时，由于条件和问题涉及的是力在空间上的积累，则暗示学生可选择力和运动、功和能量两种观点。解决问题F、G、H时，条件和问题涉及的是力在时间上的积累，则暗示学生可在力和运动、动量和冲量观点中作出选择。

学生能够做出以上的分析和决策，主要是通过使用隐性知识。学生首先将之前三种观点的内容和应用储存在大脑中，然后依据题目提供的条件和问题，逐一将二者进行比对，最后将相似度最高的观点作为结果。学生学会使用隐性知识来选择解题观点，解决问题中的“角度”问题，能够自由应对高中物理的“一题多问”。

二、隐性知识在建立解题思维中的作用和价值

学生在解决一个具体问题时，一般会依次经历下面的环节，最终形成完整的解题思维。

1.建立模型。学生通过审题，将题目中抽象的文字叙述转化为具象的、可视化的物理模型，呈现出现象、事实、情景、状态、过程等信息。在“板块模型”中，学生通过审题要在头脑中思考木板、木块各自初始状态的速度、所在位置和二者的相对位置;末态共速时各自的速度、所在位置和二者的相对位置。之后，把它们转化成可视化的实物模型，并将关键条件在图中标明，如图1。对于其他多过程、多物体模型，学生要依据情景将全程进行分段，形成分过程;并且明确每个分过程的参与者，即研究对象。这个建立模型的过程，就是隐性知识。

2.区分条件。题目提供的条件可以分为已知条件、隐含条件和干扰条件，学生要学会利用已知条件，挖掘隐含条件，排除干扰条件来解决问题。“板块模型”例题中的小木块质量m、木板质量M、动摩擦因数μ都属于已知条件，学生在解题过程中要对其加以充分使用，借助这些已知量去表达未知量。题干中提到的地面光滑，就属于隐含条件，暗示木板和地面之间没有摩擦力;木板足够长也是隐含条件，暗示无论小木块相对木板的位移是多大，都不会从木板上掉下，二者最终共速的情形一定能成立。发现这种暗示，就是学生挖掘隐含条件的过程。在题干中提到木板的厚度h，与要解决的问题毫无关系属于干扰条件，学生要将其排除，不予考虑。这种利用已知条件、挖掘隐含条件、排除干扰条件的过程就是隐性知识，是解题思维中的关键组成部分。

3.生成思维模块。在前面分析的基础上，学生将解题所需的显性知识与模型中的一个分过程进行对应和结合，生成一个独立的思维模块。模型中的分过程越多，生成的模块也越多。另外，确定解题切入点、明确解题关键也将独立生成为思维模块。这个生成各种模块的过程，就是隐性知识。

4.建立连接。学生对已经形成的多个思维模块进行比较，依据解题需要将其排序，然后将它们连接起来，形成一个链条，就生成了解题的思维。这个比较、排序、连接的过程，就是隐性知识。形成的思维链越长，说明思维就越深入;越完整，说明考虑问题越全面;思维模块越丰富，说明思维就越精细、缜密。

三、隐性知识在选择解题方法中的作用和价值

学生在分析“板块模型”时可以“一题多解”，公式法、图像法等多种方法供选择。在公式法中，解决问题C、D时，既可以选择运动学公式，又可以选择动能定理来解决。解决问题E时，既可以选择功能关系，又可以选择能量守恒定律对热量求解。解决问题F时，既可以选择运动学公式，又可以选用动量定理。另外，在运动学公式中，学生还可以在速度公式、位移公式、平均速度定义式三种方法中做出选择求解时问。解决问题G、H时，既可以选择冲量的定义式，又可以选择动量定理。但是，不同的方法对应的解题过程繁简程度不同，学生可以以省时、便捷为原则确定最佳方法。可见，选择方法的过程就是隐性知识，它可以帮助学生提高问题解决的效率，同时还解决了解题的“灵活度”和“精准度”问题。

四、隐性知识在分析同类模型中的作用和价值

“板块模型”还可以“一题多变”。“板块模型”中小木块与木板之间的摩擦力为恒力，属于特殊情况。下面三个模型中，物体之间的相互作用力是变力，属于一般情况。求解共速时的速度和系统损失动能的去向问题时，尽管模型特点稍有区别，但是蕴含的物理规律、解题的思维和方法是完全相同的。

1.子弹打木块模型。例如：质量为m的子弹，以初速度v₀射入光滑地面上静止的木块M，并留在其中。求整个过程中子弹和木块组成的系统产生的热量。

2.两块夹弹簧模型。例如：质量分别为m_A和m_B的滑块之间用轻质弹簧相连，水平地面光滑。m_A、m_B原来静止，在瞬间给m_A一个很大的冲量，使m_A获得初速度v₀则在以后的运动中，弹簧的最大势能是多少？

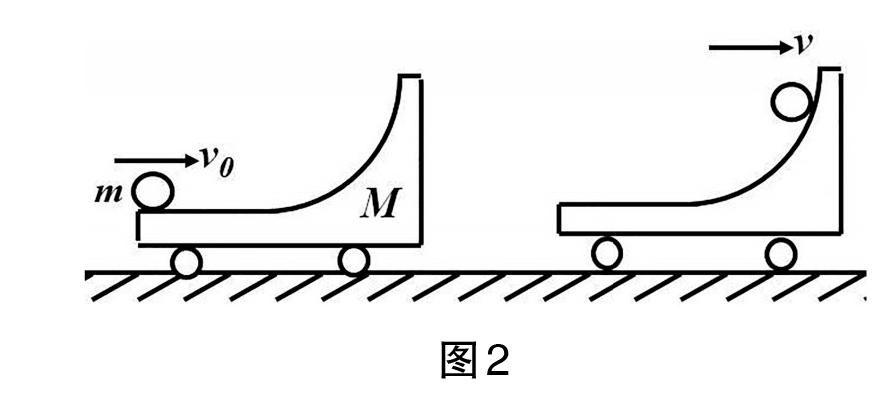
3.球轨模型。例如：如图2，带有1/4光滑圆弧轨道质量为M的滑车静止置于光滑水平面上，一质量为m的小球以速度v₀水平冲上滑车，到达某一高度并不脱离轨道。求小球到达最高点时增加的重力势能？

加上“板块模型”，四个模型共同的特点是系统在水平方向都符合动量守恒，并且模型中的物体最终共速;区别在于不同模型中系统损失的动能最终转化的能量形式不同。学生比较四个模型，找出相同点和不同点的过程就属于隐性知识。学生利用之前分析“板块模型”所形成的思维对其他的三个模型进行分析，只需稍做调整，就可以将问题解决掉。隐性知识帮助学生在变化的形式中找到不变的原理和规律，做到了“举一反三”，解决了学习的“广度”问题。

综上所述，隐性知识对问题的解决起着最直接的作用，成为培养学生科学思维的重要手段和途径。高中物理教学要重视对隐性知识的挖掘和使用，给学生打造平台、创造机会，促进思维的发展和学科素养的提高。

（责任编辑 徐德明）