浅谈光场信息的记录与重构
——实现景物影像真实三维显示的新途径
孙延禄
自上世纪50年代以来,用电子计算机研究信息处理,并将它与光学的规律、手段等结合在一起,逐渐形成了光学信息处理新领域。七十多年来,随着科技的迅速发展,数字计算机与数字图像传感器的结合日益紧密,已经创造了一个强大的称为 “计算成像”(Computational Imaging)的新工具。数字光场成像是它的一个重要组成部分。
1 光场与全光函数
光场是三维世界中光线集合的完备表示。与传统的摄影成像只记录光辐射在二维平面上的投影强度不同,光场成像则需要捕获景物光辐射的完整分布,为此就需要捕捉多维度的光辐射信息并对其进行计算成像处理,最后通过不同的显示装置显示出所需要的景物影像。
光场的概念最早于1936年由俄罗斯学者戈尔顺(Gershun)提出,它从理论上定义了空间内每个方向上通过每个点的光辐射,但却限于当时的技术条件无法实际测量与记录它。1991年,埃尔森 (E.H.Adelsion)等根据人眼对外部光线的视觉感知,提出了用七维函数来表征几何光线的空间分布,并称之为全光函数 (Plenoptic Function)。如图1所示,在全光函数L (x,y,z,θ,Φ,λ,t)的七个变量中,x,y,z表示空间中任一点的三维坐标,θ和Φ表示通过该点的一条光线的传播方向,λ表示光线的波长,t则表示时间。

图1 全光函数L的七个变量
根据文献 [2]的论述,要在图像感光器件只有二维的感光平面上记录图像全部信息,就必须至少把这七个变量中的五个先离散化 (即把它们连续变化的量替换为离散的数列)。随着影视技术的发展,已经逐步解决了这个问题。首先是t,需按照所选定的拍摄频率确定出时间序列;然后是λ,需按照显示彩色图像所要求的三原色选定R,G,B三个波长序列。这样,七维函数就变成为五维函数L(x,y,z,θ,Φ)了。要在计算机内处理这个五维函数,仍然数据量很大。为了进一步减少全光函数的维度,拉沃伊 (M.Levoy)和汉拉哈姆(P.Hanrahan)于1996年提出了利用两个相互平行的平面来对光场进行参数化表征的构想,如图2所示。即光场可以变为具有四个自变量的四维函数L (u,v,s,t)。

图2 四维函数L (u,v,s,t)
这个五维函数是怎样演变为四维函数的,其依据在哪里?在现有文献中却难以找到。本文下面对这个问题作一些推导,以证明这个降维变换的合理性。

图3 一个点在直角坐标系和球面坐标系中的表示方法
为了能说清楚此问题,需要先说明空间中同一个点在直角坐标系和球面坐标系中的表示方法及相互转换关系。如图3所示,空间内的任意点P在直角坐标系O-XYZ内表示为P (x,y,z),而P点在以O为圆心的球面坐标系中则表示为P(r,θ,Φ),其中r为矢量OP的长度,θ为OP与Z轴间的夹角,Φ为OP在XOY平面上的投影OR与X轴的夹角。根据立体解析几何,P点的直角坐标与其球面坐标间的关系为:

由式 (1)得:

由式 (1)可见,x、y、z都是r、θ和Φ的函数,只要r、θ和Φ的值确定了,它们的值也就确定了。
那么,上述五维函数L (x,y,z,θ,Φ)中的θ和Φ能否改由直角坐标系中的坐标来表示呢?回答是肯定的。

图4 全光函数降维说明
如图4所示,P点是在坐标系O-XYZ中的任一个点,我们以P(x,y,z)点为原点作出另一个坐标系P-XYZ,而且其三个轴线PX、PY、PZ均依次平行于坐标系O-XYZ的三个轴线OX、OY、OZ。
依据上述公式 (1),只要预先给定θ和Φ的值,再任意给定球面半径r一个大于零的数值,就可以求出与之对应的一点P在坐标系P-XYZ中的坐标值 (x,y,z)。这样,P点在坐标系O-XYZ中的坐标值 (x,y,z)就可以按下式求得:
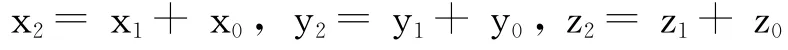
根据上述,五维函数 L (x,y,z,θ,Φ)就可以改写为L (x,y,z,x,y,z)。
光线PP的位置和方向可由P和P两点的坐标 (x,y,z,x,y,z)来确定。如果认为其中的一个点是景物上的一个发光点,另一个则可以认为是观察者的眼点或空间中的另一个点。
为了能进一步减低此函数的维度,使它变为一个四维函数,就必须把上述的六个自变量中的两个给予确定的数值。例如我们选择z、z给其两个不同的确定值 (亦即选定了两个相互平行的垂直于Z轴的平面),则在这样的约束条件下,在由z、z两个相互平行的平面内,并与它们相交的任一条直线的位置及方向就可以用一个四维函数 (x,y,x,y)表示了。
以上就是全光函数为何可以从原来的七维函数降维为四维函数L (u,v,s,t)的依据。
此外,笔者还认为这一降维构想的来源和已有一百多年历史的集成摄影术 (Integral Photography)有紧密联系。众所周知,集成摄影术的原理是20世纪初由法国人立普曼 (G.Lippmann)首先提出的。集成摄影术以采用特殊的感光板为基础,它是由众多光学上相互隔离的透镜单元组成的透镜阵列,在透镜的后焦平面上敷有感光乳剂。集成摄影能记录与再现景物的三维光学模型,观看者可以不借助于任何辅助装置,从空间的不同位置直接观看。
在集成摄影过程中除了记录发自景物的光束强度之外,还同时记录其传播方向。
为了解释集成摄影的物理实质,可以很方便地利用几何光学的概念。

图5 集成摄影的物理本质说明
如图5所示,我们在平面2上建立坐标系X,Y由物体1发出的光束与平面2相交。我们观察由物体上A点发出的一条与平面2相交于X,Y点的光线。从物体1上所有点发出的光线也汇聚于该点。这些光线的辐射强度决定于物体相应部位的亮度,但这些光线的传播方向均不同于我们所选定的那条光线。为了保存由物点A发出的这条光线的传播方向信息,在平面2的后面在与之相距d的位置设立另一个平行于平面2的平面3。在平面3上建立坐标系X’,Y’。设定由物点A发出的这条光线与平面3相交于X’,Y’点。这样一来,X,Y及X’,Y’四个坐标就单值地确定了由物点A发出的这条光线的路径。而函数F (X,Y,X’,Y’)则表示该方向上光线的辐射强度。
为了记录信号在平面3处放置感光板。要在感光平面的二维坐标内记录包含有四个变量的信号,至少要对四个变量中的两个进行离散抽样。在平面2处放置具有许多微小圆孔的网板,其相邻孔间距为X
,Y(如图5中平面2的右下部分所示),就可以使变量X,Y离散化。这样一来,整个系统就和众多的针孔相机相似 ,在感光板平面上会形成众多个被摄物体的微小影像,其数量等于网板上圆孔的数量。图中以An’表示物点的一个影像。上述过程的结果是在平面感光板上记录下以四维函数F (X,Y,X’,Y’)表征的信号。变量X,Y相当于图2中的u,v;而变量X’,Y’则相当于图2中的s,t。
因此,我们可以认为集成摄影术就是光场成像的源头,数字光场成像技术是集成摄影术的继承与发展,是集成摄影术与计算机图像处理技术相结合的近代产物。
2 光场信息的记录方法与相关装置
根据景物的状态和基线长度 (即视点范围宽度)等的不同,用摄影方法捕获景物光场信息的方法和相关装置可大致分为以下几类:
(1)移动拍摄的摄像机:对于静态的,且光场基线长度比较长 (从数英尺到数英里)的景物,多采用此法。用单台摄像机在连续移动中拍摄场景就可以捕捉到一个光场。在辅助设备的支持下,摄像机可以沿着一个平面、柱面或球面移动。此方法多用于文物与历史遗迹的数字记录与重现。
(2)多台摄像机阵列:为了能捕捉到动态场景的长基线光场需要有多台摄像机。如果视频摄像机沿着一维的路线排列,则当序列地快速显示这些场景时,会使人产生围绕场景运行的印象。如果将摄像机配备成二维阵列,则可以捕捉到全光场。本世纪初,美国斯坦福大学的一批计算机专家用100台低成本摄像机构成了一台多机阵列摄像系统,并对该系统的成像能力进行了实验。其结果对数字光场摄影技术的发展具有参考价值。
(3)小透镜阵列:如果视点范围展开在一条短的基线 (从数英寸到数微米)内,就可以使用一台摄像机和一个小透镜阵列来替代多台摄像机阵列。如前文所述,用透镜阵列来捕捉光场起源于立普曼发明的集成摄影技术。如果把图5中平面2上的微小圆孔改换成小透镜,它就变成一个小透镜阵列。每个小透镜记录一个从方阵上某个位置上观察到的场景透视图,这就构成了一个光场。
其uv分辨率取决于阵列内小透镜的数量,而其st分辨率则取决于每个小透镜后面图像传感器所对应的像素数。

图6 把微透镜阵列插入到图像传感器与摄像机主镜头之间
如图6所示,把一个 “场镜”置于小透镜阵列的物空间一侧,并且这样调节它的位置,使场景主体聚焦到小透镜的主面上,每个小透镜把摄入它的光线按方向分解并把主镜头光孔的像生成在微透镜之下的像素平面上。这样光场就被换位,此时其st分辨率取决于小透镜的数量,而其uv分辨率则取决于每个小透镜后面所对应的像素数。
上述第一种布置具有体积薄的优势,然而由它计算得出的视图的分辨率却是较低的。因此,如果系统的厚度不太受限,就应当优先选择后一种安排。在后一种安排下,只有 “场镜”需要矫正像差,而不需再去矫正每个小透镜。基于这一优势,连同现今制造微小透镜工艺的进步,众多研究者都建议把微透镜阵列插入到图像传感器与摄像机主镜头之间,从而构造成一台全光摄影机。
3 实现场景真实三维显示的新途径
电影技术的基本发展规律是通过人造手段 (包括直接摄取与计算机生成)提取并再现所记录景物的活动影像,以及声音等其他感官信息,使观众对其感受的效果逐步逼近于现实生活中的实际感受。从这一观点出发,电影技术虽然已经有了一百多年的发展历史,但目前还远未达到上述目标。仅从景物的空间再现效果来看,就有着明显的差距。目前流行的3D电影采用的是双眼视差立体显示方法。它具有许多先天性的局限性,特别是观看者眼睛“调节”与 “会聚”的冲突,长时间观看会造成眼部的不适与疲劳。因此只能说,它只是利用人眼 “错觉”的一种假3D,还只是实现3D影像显示的初级阶段。
近年来,随着电影的数字化及与计算机技术结合的日益紧密,人们在缩小这一差距方面已经开辟了许多新途径。国内外许多研究机构和高校已经发表了许多学术论文介绍其研究结果。其中尤为突出的就是基于光场重构的真实三维显示技术。
如本文前面所述,景物的光场信息本身就是多维度的光辐射信息,通过专用装置将其捕获之后,将耦合后的数据流送入计算机进行处理,得出与所选用显示系统相匹配的能正确显示该景物的控制信号并通过该显示设备重建出逼近于景物原始光场的再现光场。能重构光场的显示技术不只一种,常见的有体素点三维显示、全息显示及集成成像显示。前两种均可在空间中重构出景物的真三维影像,但其所需处理的数据量都更巨大,受到计算速度及传输速率方面的限制,且在成像质量方面也尚有许多不足之处。集成立体成像技术具有以下突出特点:(1)在不需要任何观察设备的情况下,在空间中再现了三维图像,并保留了正确的显示比例而不受观察距离的限制;(2)给观察者提供了连续视点及全视差的真实立体图像,克服了观察者眼睛的汇聚与调节的冲突问题;(3)它是一种被动显示技术,克服了全息显示技术中需要辅助光源来显示立体图像的问题;(4)系统的组成设备相对比较简单。因此,集成成像光场重构技术就更加得到研发者的青睐。
集成成像光场重构技术利用空间发光方向调控的阵列显示器集成方法重构空间景物三维光场,它无需任何机械扫描系统,采用众多显示器与光场调节屏幕组成集成化的光场重构系统。每个显示器显示的图像为特定三维区域不同视角图像的组合。通过阵列显示器图像的集成重构出三维景物的空间光场。
4 结语
相对于传统摄影方法,数字光场摄影有许多优势。限于篇幅,本文未做全面介绍。由于光场摄影捕获景物光辐射的完整分布,在后期计算机处理过程中可根据未来要求的不同影像显示方式来进行不同的影像处理。也就是说,只要进行一次拍摄,就可以在后期制作出不同技术类型的影片。显然,这十分有利于多品种影片的制作与发行,并降低其制作成本。
美国的Lytro公司已经开始了把数字光场摄影技术用于电影制作的研究,并于2016年推出了Lytro Cinema系统。虽然该公司已于2018年宣布倒闭,但其技术定会有其他公司转接而得以延续。电影技术的进步与摄影学的进步密切相关。当前,计算摄影学——全光视觉信息的计算采集已是前沿科研热点,值得我国电影科技界的重视。

