基于博弈论复合标底模型的应用研究

北京农业职业学院，北京 102442

1 引言

博弈论作为数学领域的一个分支，被越来越多的用在了分析、描述各个领域现象的工具，其在经济领域的研究和发展尤为深入，诺贝尔经济学奖，在1994 年授予了三位博弈论科学家，到目前为止，已有6 届获诺贝尔奖的科学家与博弈论相关。博弈论已深入渗透到人们生活、工作的方方面面。

博弈自古有之，大到国家战略，如战国时期的远交近攻，合纵连横；小到棋牌对弈，方桌之上黑白子之间的博弈厮杀。只不过过去的博弈哲学是松散的，没有形成系统的理论体系，通过近百年的发展研究，尤其是非零和博弈、不完全信息博弈理论获得发展以后，博弈论从数学的运筹学学科，逐渐演变成为了主流经济学研究的主要方法之一，博弈论在经济学中的应用目前广泛而成功［1］。招投标是经济活动的重要内容之一，怎样从众多的竞争对手中脱颖而出，最终获得博弈的胜利，成了博弈论研究的对象。

2 招投标中的博弈

随着市场的规范，法律法规的健全，招投标已经成为工程领域不能逾越的经济活动［2］。在招投标活动中没有亚军，只有冠军，招标、中标单位都希望利益最大化，彼此的平衡点就是最优博弈的解，在已知信息的情况下建立最优模型，是各个投标单位中标的关键。

2.1 招投标中的博弈主体

招投标中的主体主要涉及招标方（或叫甲方、业主方）、投标单位（或叫乙方、施工方），次要主体主要涉及招投标公司（第三方机构）、评标专家和监督机构等。其中招标方和投标方都希望利益最大化，存在博弈关系；投标单位和投标单位之间中标是第一目标，存在着激烈的博弈关系。博弈主体形成两个阵营招标和投标单位，博弈规则主要由招标单位决定，其与投标单位不存在竞争博弈只是利益博弈，而投标单位之间是中标和不中标的博弈，他们之间属于最激烈的博弈关系。

2.2 不完全信息的静态博弈

参与博弈的局中人中所享有的信息量，对博弈的结果有着重大的影响，如果每个参与人对其他参与人的支付（偏好）函数有完全的了解，并且支付函数是所有参与人的共同认知，这种博弈过程称为“完全信息博弈”［3］。招投标活动中，局中人彼此不能完全知道对方采购渠道的产品价格或人力成本等等。至少有一个参与者不能确定另一个参与者的收益函数，称为不完全信息博弈，也称贝叶斯博弈。在招投标中每一个参与人都知道自己的收益函数，而其他参与者的收益函数不能完全确定。招投标需要研究建立非完全信息同时（静态）行动博弈的标准描述方式。

2.3 招投标的机制设计

确定了博弈规则，在招投标中就是评标方法的具体确定，让参与者能共同遵守。投标机制的设计实际上就是找到一种纳什均衡点，既保证甲方在付出一定利益的情况下，能保证有质量的完成目标，又能让乙方有利益可图。利益永远是行动的驱动力，因此，机制设计过程要使理性的参与者有兴趣接受所设计的机制，至关重要是合理的标底。机制的设计出来要使参与者在该机制下获得的必须不低于他不接受整个机制时获得的，这样参与者会主动积极的参与到活动中来，并自动遵守执行该机制。

在不知道参与者的情况下，在投标书的制定中，设计的机制还要考虑使参与者有积极性参与招标单位希望的行动，避免出现不希望的结果，例如从事相关项目的多少、质量、信誉等，给予好企业更多的中标机会。影响招投标的信息还有很多，例如腐败、串标等不法行为，在此不做讨论，仅就招投标中常用的复合标底展开讨论研究。

3 复合标底数学模型的建立

标底是招标单位组织专门人员或委托第三方，根据要求通过系统的评估、计算得到的工程施工的预期价格［4］。招标单位拟建工程的预算金额是投标单位编写投标书的重要依据，它明确了招标单位在财务上应承担的义务。

3.1 复合标底

随着科学技术、工程领域发展的加快，以较早定额确定的标底，不能充分反应先进的材料设备水平、技术水平和管理水平等，若以此为标底不利于甲乙双方的合作质量，在此情况下，很多招投标采用了复合标底的标底报价方式，标底由招标单位和投标单位共同制定，二者是动态博弈关系。通常复合标底计算公式为：

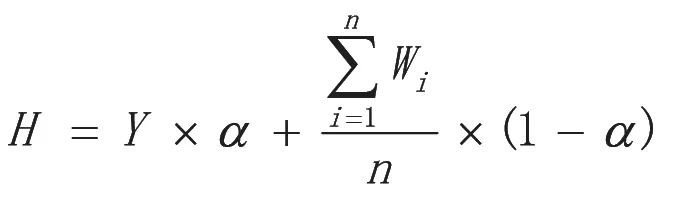
其中：H 表示复合标底，Y 招标人标底，W 不同投标人的报价，α 为标底权重系数。

如果投标人数大于3 个单位，复合标底计算时明显高于或低于标底的报价，可以剔除，避免出现不符合实际的复合标底金额。符合标底实现了价格合理性和竞争性的有机结合，随着管理水平的提高，提高效率，更有利于合理竞争降低报价，有利于公平、公正、公开的招投标环境。复合标底是衡量投标单位报价的准绳，有了复合标底，才能正确判断投标报价的合理性和可靠性，为评标、定标的提供了重要依据［5］，保证工程质量。

3.2 模型建立的基础

任何数学函数的计算都建立在一定的基础之上，这样结果才有意义。模型的建立包括模型中的要素，博弈的类型。招投标在博弈论模型中的建立首先应是利益最大化原则［6］，因为招投标中只有冠军没有亚军；其次，招投标中利益各方应诚实守信，不得通过不正当手段影响招标结果；第三，合理使用经验数据，减少为模型的不确定性，增加结果的准确性。

3.3 复合标底博弈模型的建立

根据复合标底的计算公式，建立支付函数：Z=K+ΔZ，Z表示投标人报价，K 表示初始预算值，ΔZ 表示决策计算后调整的金额。最优报价在复合标底基础上的下浮率用λ 表示，最高分的报价金额W=（1-λ）×H，W 值函数有极限，并且有最优解。因为投标报价的竞争性，函数的最小极限就是投标报价的最优解。为了在投标中获得高分，投标报价总是向着最贴近复合标底的最优分值靠近，因此W 与各投标报价的平均值的关系为投标人一次又一次复合的关系。经过递推则有Wi+1=（1-λ）［αY+（1-α）Wi］，当i=0 时，W1=（1-λ）K；当i=1 时，W2=（1-λ）［αK+（1-α）W1］；当i=n 时，Wn+1=（1-λ）［αK+（1-α）Wn］。当n 趋近于无穷大时，（1-λ）n趋近于零，这时Wn+1≈Wn，两者等价，则，该公式关键在利用定额及相关文件计算预算值K 的准确性，他决定了报价最高分的金额，如果招标业主提供了K 值，可以直接带入公式计算最优投标金额。

4 实例应用研究

4.1 项目基本情况

某院校楼宇智能化实训中心建设项目，业主标底为2928356 元，采用复合标底报价评分的办法，其中报价分占标书总分的60%，复合标底满分为60 分，招标书中明示的标底占开标时合成报价的65%，剩下的35%由投标企业的有效平均总报价组成。为了约束企业，投标企业报价在复合标底的90%～102%范围内为有效标，投标企业报价是复合标底的-4%时，报价评分则最高。高于复合标底的96%时，每超过百分之一扣8 分，低于96%时，每低于百分之一扣5 分。

4.2 投标报价博弈

根据3.3 中构造的复合标底模型，依次循序计算，为简化计算假设：

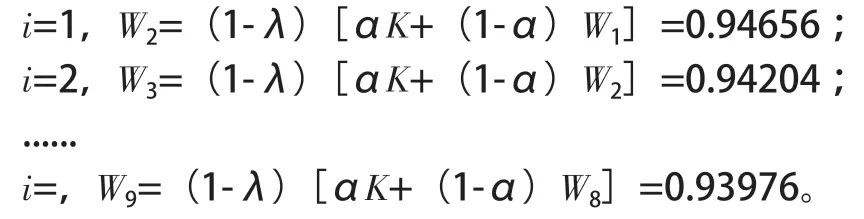
结果如下表所示：

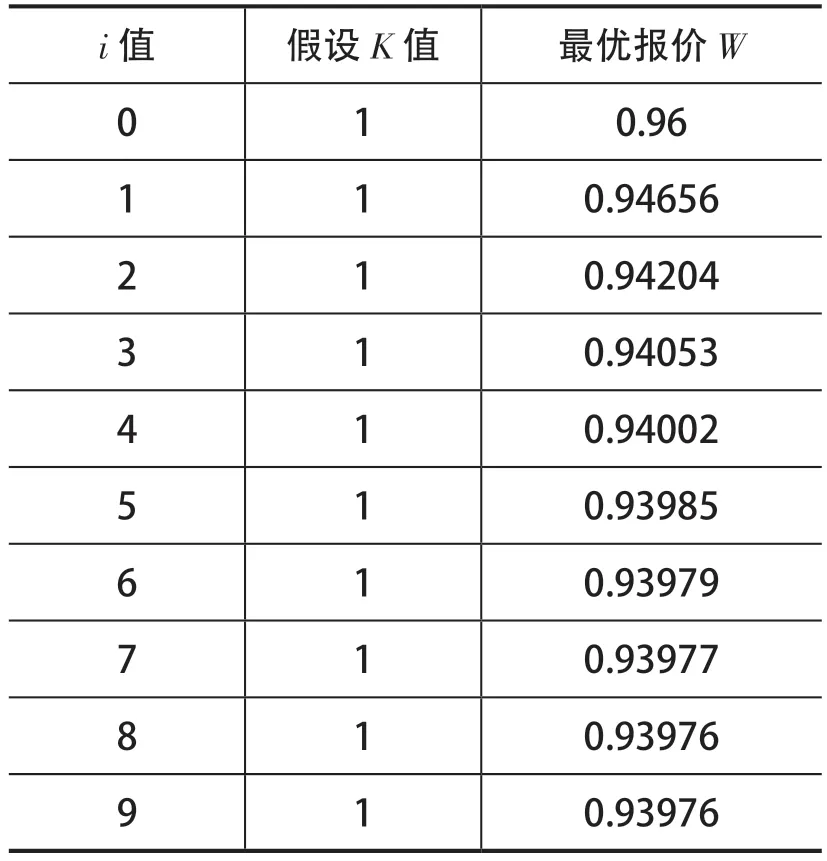
表：模拟计算表

当i 取值7 以后最优报价值变化基本可以忽略不计，因此最优报价W=0.93976×2928356=2751952元。已知α=65%，λ=40%带入公式：

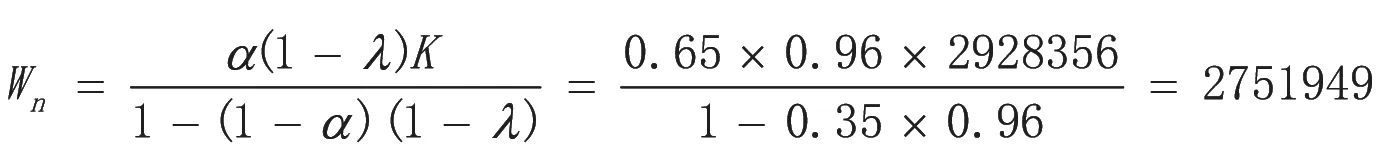
通过以上计算，投标公司最优报价可定为2752000 元。

5 结语

随着商业市场的规范，博弈论在招投标领域的应用会越来越广泛，博弈中用最优策略实现利益的最大化，用科学严谨的数学计算代替经验。复合标底的评分办法也只是评标的一种方式，在招投标中也只是占有部分分数，影响招投标结果的因素还有很多，诸如甲方喜好，评标专家认知，监督、诚信、业绩等等的因素，贯穿招投标的整个过程，博弈也将如影随形［7］。随着招投标制度的推行，投标企业面临的竞争在增加，投标失败的风险也在加大，如何采取更有效的投标策略是第一步，也是最重要的一步！与时俱进，更需要在分析复合标底前提下，利用博弈论理论确定合理最优报价，一举中标并获得丰厚的经济效益。