广义强色散DGH方程的不变子空间和精确解
李雪霞 刘汉泽 常丽娜
(聊城大学 数学科学学院,山东 聊城 252059)
0 引言
非线性偏微分方程在物理、化学、生物等领域的模型研究方面,起着至关重要的作用,寻找非线性微分方程精确解也是数学研究的热点之一,目前构建非线性偏微分方程精确解的方法主要包括:李对称法、首次积分法、指数函数展开法和(G'/G)-展开法、不变子空间法等.不变子空间方法起源于李群分析,其实质是通过构造非线性偏微分方程(PDE)的不变子空间,将非线性PDE转化为常微分方程(ODE)组,通过求解ODE组的解得到原非线性PDE的解.其最初是由Galaktionov等提出,后来经过多位学者扩展并得到了广泛应用,例如,得到了Hunter-Saxton方程、可压缩欧拉方程等的精确解[1].
不变子空间方法的突出特点是适用范围广,它是一种与对称群相关的方法,通过这种方法,非线性演化方程可以被约化为有限维动力系统;同时它也是一个算法,可以为非线性偏微分方程构造更多的孤子解和相似解.但是不变子空间方法还有许多问题需要继续研究,例如如何根据不同的非线性方程,构造出更多的精确解;再者,如何提高求解常微分方程组的效率,比如借助Maple程序,等等,都需要进一步研究.
1993年,Camassa和Holm得到了一类完全可积的非线性的新型浅水波方程Camassa-Holm方程[2]
ut+2aux-uxxt+3uux=2uxuxxx+uuxxx.
(1)
方程(1)具有双Hamilton结构,并完全可积.a≠0时,具有光滑孤立波解;a=0时,方程(1)具有形如u=ce-|x-ct|(c为速度)的尖峰孤立波解(peakon).
Dullin,Gottwald和Holm利用一类浅水波方程非局部渐近形式推导出DGH方程
ut+2aux-uxxt+3uux+γuxxx=2uxuxx+uuxxx,
(2)
其中uxx是线性色散项,当γ=0时即为Camassa-Holm方程,当色散项为(u-uxx)xxx时,则方程即为广义强色散DGH方程,它描述了浅水流中曲面波的单向传播
ut+2c1ux-uxxt+c2uux+γ(u-uxx)xxx=2uxuxx+uuxxx,
(3)
其中u=u(x,t)为未知函数,c1,c2,γ为任意常数.
近年来,许多学者对DGH方程也做了许多研究,2007年,田立新对DGH方程的哈密尔顿结构和解的整体存在性及Blow-up现象进行了研究.郭柏林和刘正荣通过使用平面的自治系统的定性分析研究方法,研究了DGH方程的尖峰孤立波解.与其它方法相比,不变子空间方法可以得到DGH方程的许多新形式的精确解,包括有理函数解,这些解不同于对称约化解,也不同于孤立子解[3,4].
本文首先介绍不变子空间的方法原理,其次求出广义强色散DGH方程在n维微分算子下的所有允许的不变子空间.最后,我们通过常微分方程解的子空间作为基函数构造偏微分方程多项式函数,基函数构造偏微分方程多项式函数,指数函数和三角函数形式的精确解,并且在运用不变子空间方法的基础上,将方程的部分精确解以图像的形式表达出来,使DGH方程的解更加形象.
1 不变子空间方法
考虑一般的演化方程[5,6]
ut=F[u],
(4)
其中u=u(x,t),F[u]是一个k-阶微分算子,且F[u] ≡F(x,u,ux,uxx,…).假设给定一个n维不相关的函数f1(x),…,fn(x),那么可以得到n维线性组合的子空间Wn=Ω{f1(x),f2(x),…,fn(x)}.对于给定的微分算子F,如果满足F[Wn]包含于Wn, 则称算子F允许线性子空间Wn, 即线性子空间Wn在F算子下被认为是恒定的,即存在n个函数φi(c1,c2,…,cn),满足
其中C1,…,Cn为任意常数,那么方程(4)有形如
(5)
的解,其中ci满足n维动力系统
φ′(t)=φi(φ1(t),…,φn(t)),i=1,2,…,n.
(6)
如果是由n阶线性常微分方程[7,8]
L[y]≡y(n)+an-1(x)y(n-1)+…+a1y+a0y=0
(7)
的解空间来定义k阶微分算子F允许的子空间Wn,并在这些不变子空间中构造方程(3)的解,且(7)式中ai均表示常数,那么n需要满足的条件为n≤2k+1,并且Wn在算子F的不变条件为
L[F[u]]|L[u]=0≡0,
(8)
在以上这些不变条件下,就可以得到方程(3)解的形式,并且可以求出精确解,下文中使用的符号
2 广义强色散DGH方程的不变子空间
2.1 二维不变子空间
首先将方程(3)写作一般演化方程(4)的形式
ut-uxxt+γ(u-uxx)xxx=2uxuxx+uuxxx-2c1ux-c2uux,
(9)
方程右边的非线性算子F为
F[u]=2uxuxx+uuxxx-2c1ux-c2uux,
(10)
式中最高次导数项k=3,则由维数定理可知,我们需要考虑n=2,3,…,7维常微分方程定义的不变子空间.在本小节,我们考虑方程(9)右边的微分算子F[u] 是由二阶常微分方程[9-12]
L2[y] ≡y″+a1y′+a0y=0
(11)
定义的不变子空间.则W2的不变条件为
L2[F[u]]|L2[u]=0=D2F+a1DF+a0F|L2[u]=0=0,
(12)

求解上述方程组,我们得到下列全部三组解
(ii)a0=0,a1=0,c1=c1,c2=c2;
(iii)a0=a0,a1=0,c1=c1,c2=-3a0.
根据以上三组解,方程(9)微分算子F[u]允许定义的二维不变子空间W2为
2.2 三维不变子空间
假设微分算子F[u]是由三阶常系数线性方程L[y]≡y‴+a2y″+a1y′+a0y=0的解空间所定义的不变子空间,其不变条件为
L[F[u]]|[H]=(D3F+a2D2F+a1DF+a0F)|[H]=0,
(13)

求解上述方程组,我们得到了唯一的一组解{a0=0,a1=a1,a2=0,c1=c1,c2=-3a1} ,由此,我们得到DGH方程的三维不变子空间W3
我们可以从求出的二维和三维子空间中看出不变子空间方法只与方程的非线性项有关.根据上述类似的计算方式,我们可以推算出非线性算子(形如F[u])允许的由(7)式(n=4,5,6)分别定义的四维,五维和六维不变子空间,其七维不变子空间不存在.
2.3 四维不变子空间
2.4 五维不变子空间
2.5 六维不变子空间
3 广义强色散DGH方程的精确解和图像
根据上文第二部分求得的不变子空间的基函数,我们可以把广义强色散DGH方程的解分成三类,并且对应方程的三种解:多项式函数解,指数函数解和三角函数解,然后利用Maple软件画出解的图像,使方程的解更加直观.下面我们就具体以广义强色散DGH方程为例来求方程的精确解.
3.1 方程的多项式解[13-15]
由2.1中F22知,广义强色散DGH方程
ut-uxxt+γ(u-uxx)xxx=2uxuxx+uuxxx-2c1ux-c2uux,
(14)
假设有多项式形式的解为
u1=φ0(t)+φ1(t)x,
(15)

常数项
(16)
求解(16)可得
(17)
其中C1,C2为任意常数.则可以得到方程(14)的解为
(18)
方程解的图像如
3.2 方程的三角函数和指数函数解
由2.2中F3知,方程可写为
ut-uxxt+γ(u-uxx)xxx=2uxuxx+uuxxx-2c1ux+3a1uux,
(19)
假设有三角函数和指数函数形精确解
(20)
(21)
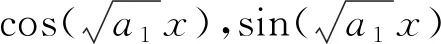
常数项φ0′(t)=0.求解上述方程可知φ0(t)=C1,φ1(t)=C2sin(At)+C3cos(At),φ2(t)=C2cos(At)-C3sin(At),由此,可以得到方程(19)的三角函数精确解为
(22)

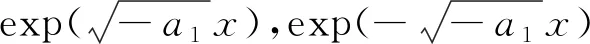
由此,可以得到方程(19)的指数函数精确解为
(23)
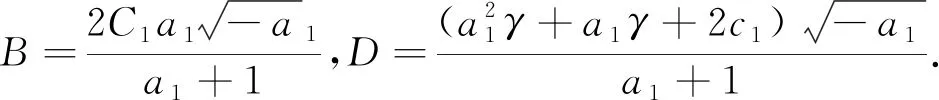
4 结语
我们只选取了部分不变子空间的基函数进行求解,得到了广义强色散DGH方程的多项式函数解,三角函数解和指数函数解.不同的基函数进行组合可以求出不同的精确解,这也使得不变子空间方法的应用更为广阔;同时,针对方程组也可以应用相同的方法进行求解,上述研究理论为以后的研究提供了方向,对于不变子空间方法还有很多理论值得我们去研究.

