双模压缩Fock态在量子相位估计中的应用
侯丽丽 王 帅
(江苏理工学院 数理学院,江苏 常州 213001)

在量子光学中,双模压缩Fock态(TMSFS)是一类较为普遍且具有一定意义的非高斯型量子态.理论上,TMSFS态可以由一个双模压缩算符作用于双模Fock态上而获得,即
|TMSFS〉=S2(r)|m,n〉,
(1)
式中S2(r)=exp[r(a†b†-ab)]是双模压缩算符,r为压缩参数.由式(1)结合双模压缩算符的Bogolyubov变换,容易得到TMSFS态的平均光子数为
(2)
根据式(2),TMSFS态的平均光子数在给定初始压缩参数r的情况下,随着双模Fock态|m,n〉的粒子数m和n增加而增大.TMSFS态最早由Chizhow等人[17]提出,该非高斯型量子态的光子数分布性质、纠缠性质等非经典性质已经得到了较详细地研究[18,19].2018年,向少华等人[20]还研究了TMSFS态的非高斯动力学演化的特征.最近,我们详细研究了对称的TMSFS态(即m=n)在MZI干涉仪的相位测量精度中的性能表现[21].研究发现,基于量子Fisher信息理论,在给定初始压缩参数的情况下,增加双模Fock态的粒子数,对称的TMSFS态可以提高量子Cramér-Rao(QCRB)界限,这一相位测量精度的最终极限.另一方面,基于宇称测量所得到的相位测量精度在待测相位很小时可以达到QCRB界限.所以,对于对称的TMSFS态,宇称测量是一种最优测量方案.
与文献[21]不同,本文将考虑一般的TMSFS态(包括非对称的情况,即m≠n)在量子相位估计中的性能表现.与双模压缩真空态相比,研究非对称的TMSFS态是否也能提高量子Fisher信息,进而改善QCRB界限.与此同时,分析宇称测量方案所得到的相位测量精度能否达到QCRB界限,即对于非对称的TMSFS态,宇称测量是否也是最优测量.另外在理论上,本文考虑的情况还包括两种重要特例:(1) 当m=n=0时,即双模压缩真空态,它作为MZI干涉仪的探测态,相位测量精度可以达到海森堡极限[22];(2) 当r=0时,即一般的双模Fock态|m,n〉,该量子态在量子精密测量中的应用也已经得到研究[8].
1 马赫-曾德尔干涉仪中的量子Fisher信息


图1 马赫-曾德尔干涉仪结构示意图
(3)

(4)

(5)
式中Hm,n(x,y)是双变量厄密多项式
(6)
这里把TMSFS态用相干态表象来表示,即
(7)

(8)
尽管式(8)的形式比较复杂,但是它却能极大地简化后文中的计算.
下面,我们首先计算TMSFS态作为MZI干涉仪探测态时的量子Fisher信息.干涉仪的相位测量最终精度由基于量子Fisher信息的QCRB界限所确定[25]
(9)
对于量子纯态作为MZI干涉仪的探测态,相应的量子Fisher信息可基于输入量子态计算给出[26]
(10)
根据式(1),经繁琐计算可得
(11)
式(11)是本文的第一个主要结果.根据式(9)和(11)容易看出,在给定初始压缩参数r的情况下,增加双模Fock态的m和n的取值,QCRB界限必然会得到提高.这主要是由于在给定初始压缩参数的情况下,TMSFS态所含有的平均光子数随着m和n的增加而增大,正如式(2)所示.因此,在给定初始压缩参数的情况下,与双模压缩真空态相比较,一般的TMSFS态是可以有效提高相位测量的最终测量精度.因此,即使是在m≠n情况下,TMSFS态依然可以有效提高QCRB界限.
特别地,在极端非对称情况下,譬如取n=0(m≠0),式(11)退化为下面的简单形式
(12)
显然,给定初始压缩参数的情况下,增加m的取值依然会有效提高QCRB界限.另一方面,若是根据探测态的总光子数,式(12)又可改写成
(13)
可见,限定探测态都具有相同平均光子数的情况下,增加m的取值反而会削弱QCRB界限.正如文献[21]所指出的,在限定探测态都具有相同平均光子数的情况下,与TMSFS相比较,双模压缩真空态在MZI干涉仪中的相位测量精度反而是最好的.量子态所含有的平均光子数是量子精密测量中的一个重要参数.由以上分析可见,TMSFS态的优势在于给定初始压缩参数时,它的平均光子数会随着m和n的增加而增大,从而导致了其Fisher信息的增大.
2 宇称测量方案与相位的测量精度
宇称测量方案是测量微小待测相位常用的一种测量方法.已经证明对于许多非经典态作为MZI干涉仪的探测态[4-6,8-11,13-15],它是一种最优测量方案.特别地,对于一类路径对称的量子态,理论上已经证明了在某些特殊相位点,宇称测量方案能够达到QCRB界限,是最优测量[27].对于一般的TMSFS态,本文主要研究宇称测量方案所给出的相位测量精度是否能够达到QCRB界限,即宇称测量方案是否是最优测量方案.
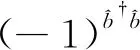
(14)

(15)
注意到以下积分公式[30]
(16)

(17)
式中〈Πb(φ)〉0是当双模压缩真空态作为MZI干涉仪的探测态时,相应的宇称测量信号
(18)
在推导式(17)的过程中,与文献[22]相同,方便起见,本文也做了一个相位变换φ→φ+π/2. 该式是本文的第二个主要结果.特别的,在r=0时,TMSFS态退化为双模Fock态|m,n〉,由式(17)可得当双模Fock态作为MZI干涉仪探测态时的宇称测量的信号为
(19)
这与文献[8]的结果相一致.
特别地,与式(12)相对应,当n=0时宇称测量信号式(17)退化为
(20)
应用勒让德多项式的产生函数[31]
(21)
式(20)还可以写成如下简洁形式,即
(22)
应用式(12)和(22)从数值上可方便的检验,对于这种非对称的TMSFS态,宇称测量是否是最优测量.
利用误差传播理论,干涉仪的相位测量精度为[28]
(23)
式中已经利用了〈Π2(φ)〉=1这一事实.当m=n=0时,把式(18)代入式(23),就得到了双模压缩真空态作为MZI干涉仪的探测态时,相位的测量精度为[22]
(24)
文献[21]已经指出,在限定探测态具有相同的平均光子数时,与双模压缩真空态相比,对称的TMSFS态并不能改善QCRB界限.从数值上可以证明对于非对称的TMSFS态的情况也是如此.因此,本文主要考虑在给定压缩参数的情况下,一般的TMSFS态是否可以改善QCRB界限,宇称测量所得到的相位测量精度是否能够达到QCRB界限.
图2(a)表示在不同的(m,n)取值的情况下,相位测量的最终理论极限QCRB界限随压缩参数的变化曲线.显然,在给定初始压缩参数的情况下,增加(m,n)的取值,是可以有效改善QCRB界限的.这一结果与式(11) 相符合.图2(b)则代表宇称测量在待测相位趋于零时(此处取φ=0.001)所得到的相位测量精度随压缩参数的变化曲线.图2表明,在待测相位趋于零时,宇称测量所得到的相位测量精度能够达到QCRB界限.因此,宇称测量对于m=n时的TMSFS态来说是最优测量方案.但是,当m≠n时的非对称TMSFS态作为MZI干涉仪的探测态时,由图3(a)可见,在给定初始压缩参数的情况下,增加双模Fock态的粒子数m和n的取值虽然可以提高QCRB界限,但宇称测量所得到的相位测量精度并不能达到QCRB界限.而且,非对称TMSFS态所提供的相位测量精度甚至比双模压缩真空态要差很多,特别是在m>1和n=0的情况.因此,与双模压缩真空态相比,在给定初始压缩参数的情况下,虽然非对称的TMSFS能够有效改善QCRB界限,但宇称测量并不是该量子态的最优测量方案.

图2 具有(m,n)不同取值的对称TMSFS态在φ=10-3时,相位测量精度随初始压缩参数r的变化曲线(a) 基于量子Fisher信息所得到的最终测量界限QCRB界限;(b) 基于宇称测量所得到的相位测量精度

图3 具有(m,n)不同取值的非对称TMSFS态在φ=10-3时,相位测量精度随初始压缩参数r的变化曲线(a) 基于量子Fisher信息所得到的最终测量界限QCRB界限;(b) 基于宇称测量所得到的相位测量精度
3 结论
本文研究了TMSFS态作为MZI干涉仪的探测态,它在相位测量精度中的性能表现,给出了相应的量子Fisher信息和宇称测量结果的解析表达式.研究结果表明,一方面根据基于量子Fisher信息理论,在给定初始压缩参数的情况下,TMSFS态可以进一步值提高相位测量的最终界限,即QCRB界限.另一面基于宇称测量方案,只有当m=n时的对称TMSFS态,宇称测量在待测相位趋于零时才是最优方案.而对于m≠n的情况,宇称测量所得到相位测量精度并不能达到QCRB界限.因此,本文研究结果也再次证明了,对于某些非经典态,宇称测量并不总是一种最优测量方案.

