基于磁流变减震器的飞机起落架控制研究
黄 敏 李世佳
(1.民用飞机模拟飞行国家重点实验室,上海 201210;2.上海飞机设计研究院,上海 201210)
0 引 言
起落架作为飞机的重要部件,直接影响起降过程的安全性.同时,起落架也是影响飞机起降性能、运营经济性与舒适性的重要一环[1].目前飞机上广泛使用的是油气式缓冲器或全液压缓冲器,虽然传统缓冲器有着结构简单、质量轻便和方便维修的优势,但是由于其阻尼力不能根据外部载荷的变化实现实时控制,使其容易损坏[1-3].并且传统缓冲器的阻尼力变化范围有限,因此其减震效果和控制策略有待提高和改进.
起落架上的缓冲减震装置可缓解飞机着陆时的冲击力,大型飞机通常采用油气式减震器减震.油气式减震器是一种被动装置,不能随工况变化主动或半主动地调节阻尼力,这会使得起落架与机体所受载荷加剧[2].当今飞机安全事故中,降落阶段出现的事故占30.00%左右,其中起落架故障造成的事故占相当大的比例.因此,新型智能减震器已经成为国内外的研究热点[3-14],磁流变减震器可以根据路况与飞机的运行状态,快速改变减震器参数使其达到优异的性能.
凯迪拉克与奥迪等品牌的部分高端汽车已经开始使用磁流变减震器,但在飞机起落架上的应用还处于空白.国内外研究主要围绕磁流变减震器的基本结构设计与控制策略2方面.贾玉红和武晓娟[8]在考虑地面噪声激励的情况下对飞机磁流变起落架的模糊控制进行了仿真,但没有考虑落震初速度;Ahure等[9]基于非线性宾汉塑性模型对半主动控制起落架进行建模与仿真;傅莉等[10]提出的基于简化模型参考的自适应控制的飞机起落架磁流变缓冲系统,经过多体动力学仿真验证该系统较传统的油液式缓冲系统有着较好的减震效果;杨永刚等[11]对起落架磁流变减震器进行鲁棒控制的研究,其三自由度模型考虑到反弹、俯仰和滚转运动,但没有考虑到轮载变形.另外,部分文献对于起落架力学模型中的阻尼与刚度进行线性简化[9-12],虽然简化后的模型能反映系统的宏观力学特性,但不能精确反映缓冲器中空气弹簧的非线性与轮胎压缩的非线性特征.对于基于模型的控制方法,如线性二次型最优控制、鲁棒控制与模型预测控制等控制方法,研究对象数学模型的构建精度会直接影响控制仿真结果.
飞机着陆时会受到地面冲击影响和地面不平度的耦合影响,因此有必要研究着陆及落震的控制策略.由于减震器表现出高度的非线性滞回性能,使用不基于模型的控制策略,如神经网络、天棚阻尼控制和模糊控制,可以避免非线性系统动力学的复杂性[9].本文针对起落架落震的特点,先建立较为详细的起落架动力学模型,并提出3种不基于模型的控制策略,通过仿真研究起落架的落震性能.
1 动力学分析与建模
1.1 磁流变减震器建模
磁流变减震器依靠线圈激励电流改变磁流变液的本构状态,从而改变磁流变减震器的输出力以实现改变阻尼的目的[2].单拉杆式磁流变减震器如图1所示,主要由线圈、拉杆、活塞、气体弹簧与磁流变液组成.
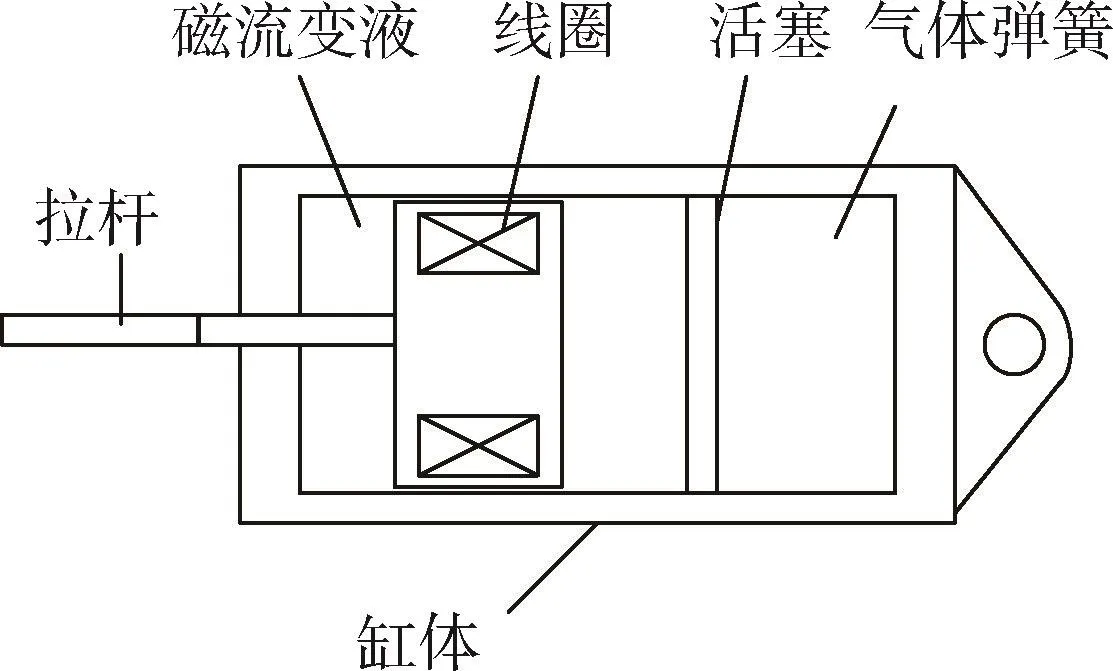
图1 磁流变减震器结构示意
Bouc-Wen辨识模型相较宾汉模型更能准确描述磁流变减震器的低速滞回特性[11-13],通常被用来描述磁流变减震器的力学特性,其结构如图2所示.通过构建基于Bouc-Wen模型的磁流变减震器力学模型来描述磁流变起落架中的磁流变力学特性.

图2 Bouc-Wen模型结构
模型方程为
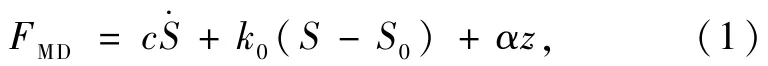
式中FMD为磁流变减震器的阻尼力,c为屈服阻尼系数,k0为阻尼器线性刚度,S为减震器行程,S0为行程起始值,为减震器行程变化率,α为屈服应力参数.z可表示为
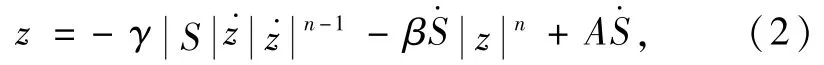
式中γ和β分别表示滞回环的宽度与高度,n是弹性到塑性的平滑度.
经过辨识和已有文献研究[12],参数α与c和通过线圈的电流(I)有关,可表示为I的一次多项式,参数ca、αa、cb和αb由数据拟合得到

1.2 起落架系统建模
借鉴汽车1/4悬架经验[14],采用二自由度模型描述起落架落震动力学,如图3所示.质量可分为簧载质量(M)与轮载质量(m)2部分.簧载质量主要受到自身重力(Mg)、磁流变阻尼力(FMD)、摩擦力(f)、空气弹簧力(Fair)与升力(L)作用.轮载质量主要受到自身重力(mg)、FMD、f、空气弹簧与轮胎支撑力(V)作用.L采用文献中的经验公式计算[6],其余变量可用如下式(4~9)计算.

图3 磁流变起落架动力学模型
气体弹簧力(Fair)为

式中Aair为气腔内横截面积,S为缓冲支柱行程,γ为气体系数,Patm为大气压力.轮胎垂直反力(V)为

式中δ为轮胎变形量,为变形轮胎速率,C为垂直阻尼系数,C1为轮胎变形系数.f(δ)反映轮胎变形量与轮胎静力的关系,可表示为二次多项式
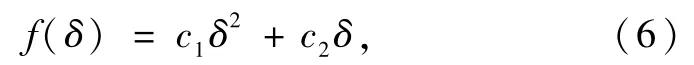
式中参数c1和c2由数据拟合得到.
δ满足公式:

轮胎位移受到地面噪声扰动(w)影响,计算式为

摩擦力(Ff)为
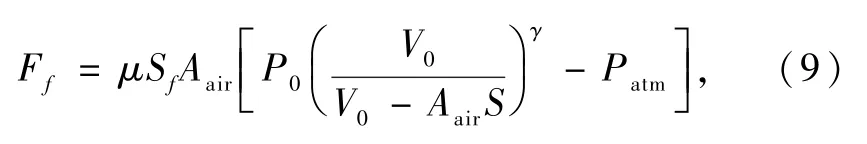
式中μ为摩擦系数,Sf为摩擦面积.
根据式(4~9)可建立磁流变起落架的动力学模型
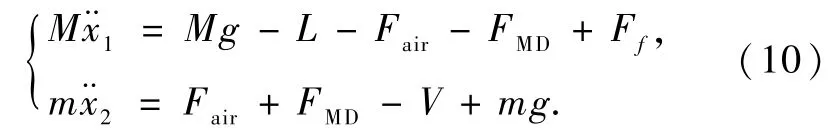
本文采用滤波白噪声作为随机路面的输入模型,如图4所示.
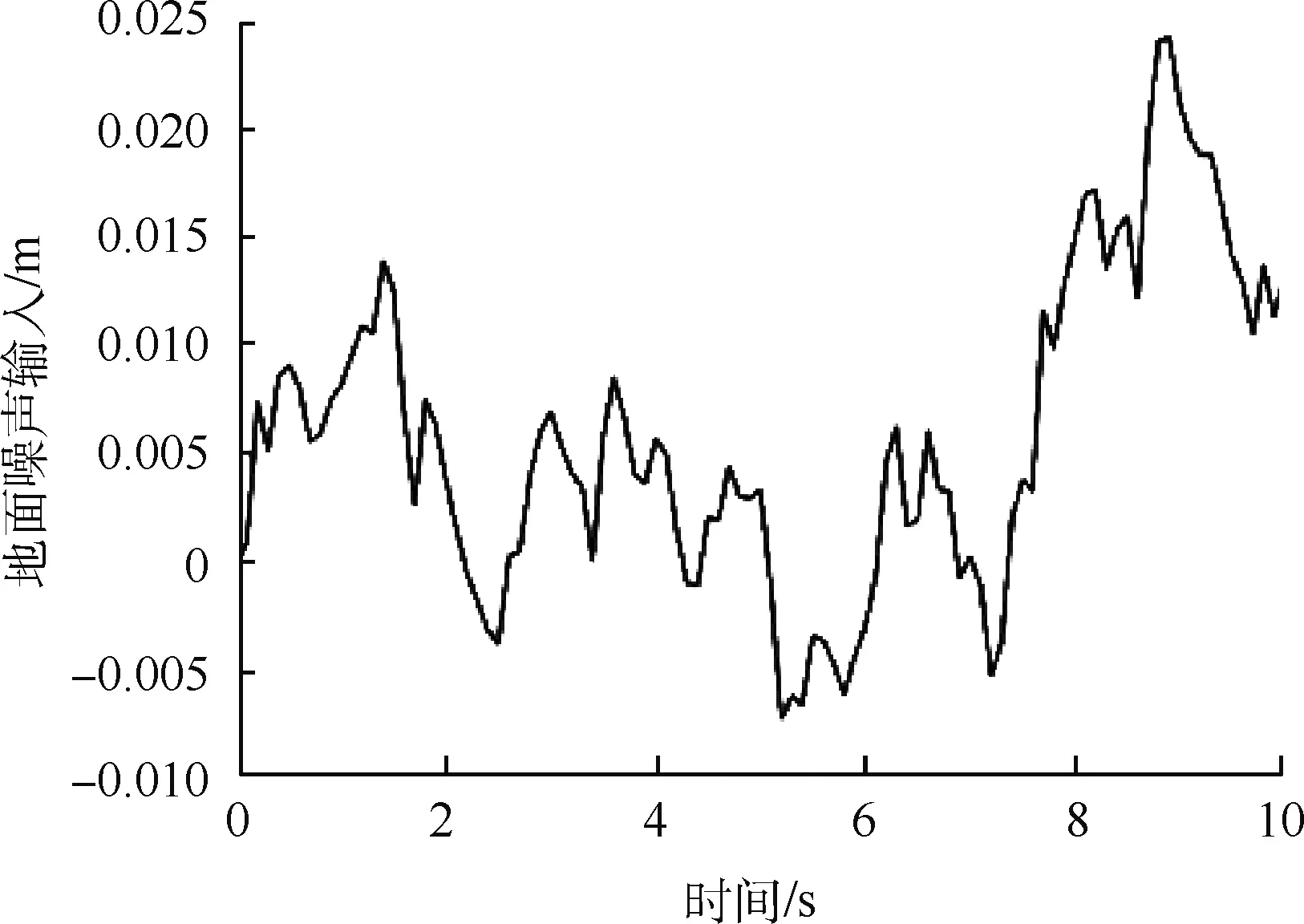
图4 地面噪声输入
2 磁流变起落架半主动控制
磁流变起落架半主动控制策略是研究如何改变线圈激励电流来改善起落架减震性能的方法.基于模型的策略对于可精确表示的系统有精准的控制能力,但对于复杂或难以精确描述的系统,则效果不佳[15-18].对于磁流变的非线性与滞缓特性,国内外学者依据实验数据建立了各种数学模型表达式[19-20],虽然部分模型已经能大致表述其力学特性,但对于复杂模型的逆模型研究还不够深入,而且与非线性的起落架动力学模型相耦合又进一步增加系统的复杂性.这使得精确的控制系统动态模式较难得到,因此,可尝试以模糊数学或最优控制来处理这些控制问题.
2.1 Bang-Bang控制
Bang-Bang控制是对于时间的一种简单的最优控制,通过将系统分为2个状态,在一个状态中取最大值,在另一状态中取最小值.磁流变起落架Bang-Bang控制策略如式(11)所示.当簧载质量的速度与活塞速度同向时,电流需要调整为最大使得阻尼力最大;当簧载质量的速度与活塞速度反向时,电流需要调整为最小使得阻尼力最小.
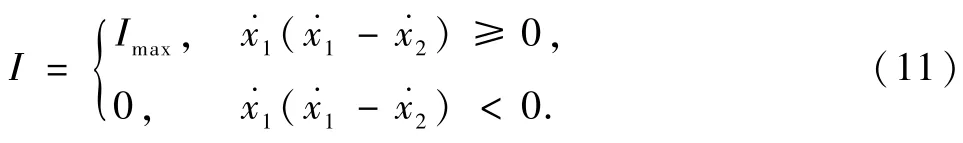
2.2 模糊控制
确定模糊控制器的输入量为簧载质量的位移(x1)与平衡状态下位移值(x0)的偏差(Δx)和簧载质量的速度(1),输出量为电流.Δx和1采用的论域为负大、负小、零、正小和正大.
通过对磁流变减震器的力学分析,以及对起落架系统的分析,并参考有关磁流变减震器控制的文献[7-9],最终通过仿真调试得出模糊控制规则集,一共有25条规律,如表1所示.输入输出的隶属度函数都为三角形函数,所得规则曲面如图5所示,xdot表示簧载质量速度的论域,Δx表示偏差的论域.

表1 模糊控制规则
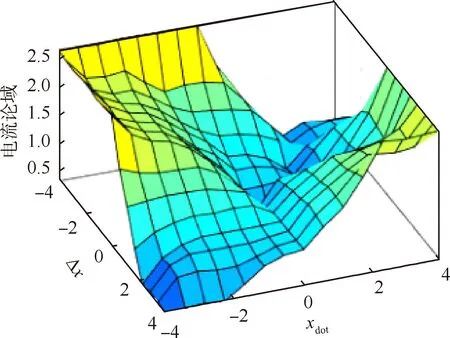
图5 模糊控制规则曲面
2.3 复合控制
飞机在跑道上着陆时,起落架会受到冲击,冲击与地面噪声会对系统产生载荷.在落震初期,系统的载荷主要由冲击产生,减震器需要消耗系统初始动能.待初始动能基本耗散之后,起落架系统主要受到地面噪声影响.所以对应不同阶段运用不同的控制策略,采用一种非模型参考的复合控制方法进行半主动控制,原理如图6所示.该控制器结合了Bang-Bang和模糊自适应控制2种控制思想.采用这种复合控制策略能充分发挥这2种控制模式的优点,有效地弥补单种控制方法的缺点.

图6 复合控制原理
在起落架落震初始阶段,影响系统动态响应的主要因素是系统的初始动能,落震运动曲线呈现振荡衰减状态形式较为规律.使用模糊控制方法控制输出到磁流变减震器的电流,待落震过程基本完成时,影响系统动态响应的主要因素转变为地面噪声,其激励情况不规律.为使控制简单化,所以使用Bang-Bang控制来控制输入电流.
控制策略判断逻辑为
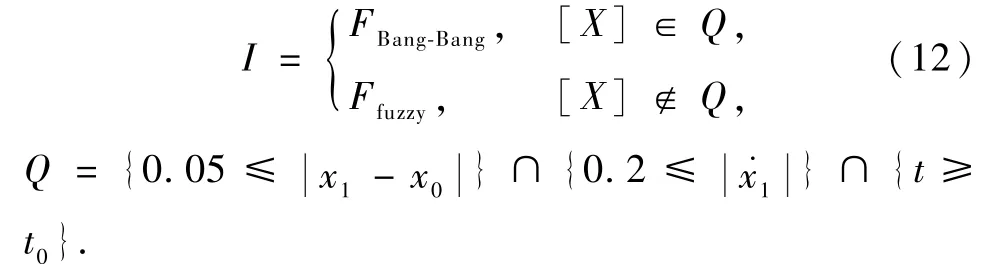
3 仿真计算与结果分析
通过Matlab/Simulink软件建立磁流变起落架系统模型,如图7所示.图中磁流变减震器模块基于式(1~3)构建,起落架模块基于式(4~10)构建.

图7 磁流变起落架系统模型
根据式(11)、(12)与模糊论域,通过 Matlab/Simulink软件分别对3种控制器进行建模,磁流变起落架系统加入控制器的仿真模型如图8所示.可通过控制切换开关在仿真前选择恒流无控制、Bang-Bang控制、模糊控制或复合控制进行仿真.
为研究3种控制方法的有效性与性能,选用某型磁流变减震器[15]与某型飞机的落震工况进行仿真研究.仿真参数如表2和3所示.

表2 磁流变减震器参数
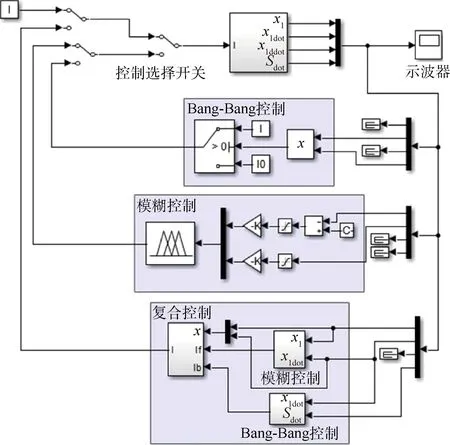
图8 控制系统仿真模型

表3 起落架参数
以初始落震垂直方向初始速度1.5 m/s进行仿真,仿真结果如图9~11与表4所示.Bang-Bang控制、模糊控制与复合控制策略较恒流被动控制结果位移峰值分别降低了5.02%、3.94%和5.02%,位移均方根分别降低了5.20%、2.10%和7.20%;速度峰值分别降低了36.50%、26.60%和36.50%,速度均方根分别降低了21.20%、14.90%和27.00%;加速度峰值分别降低了34.70%、24.80%和34.70%;加速度均方根分别降低了32.50%、26.80%和33.40%.

图9 位移-时间
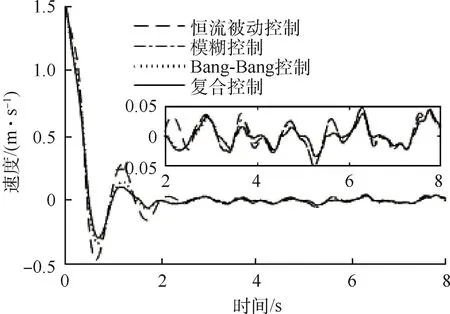
图10 速度-时间
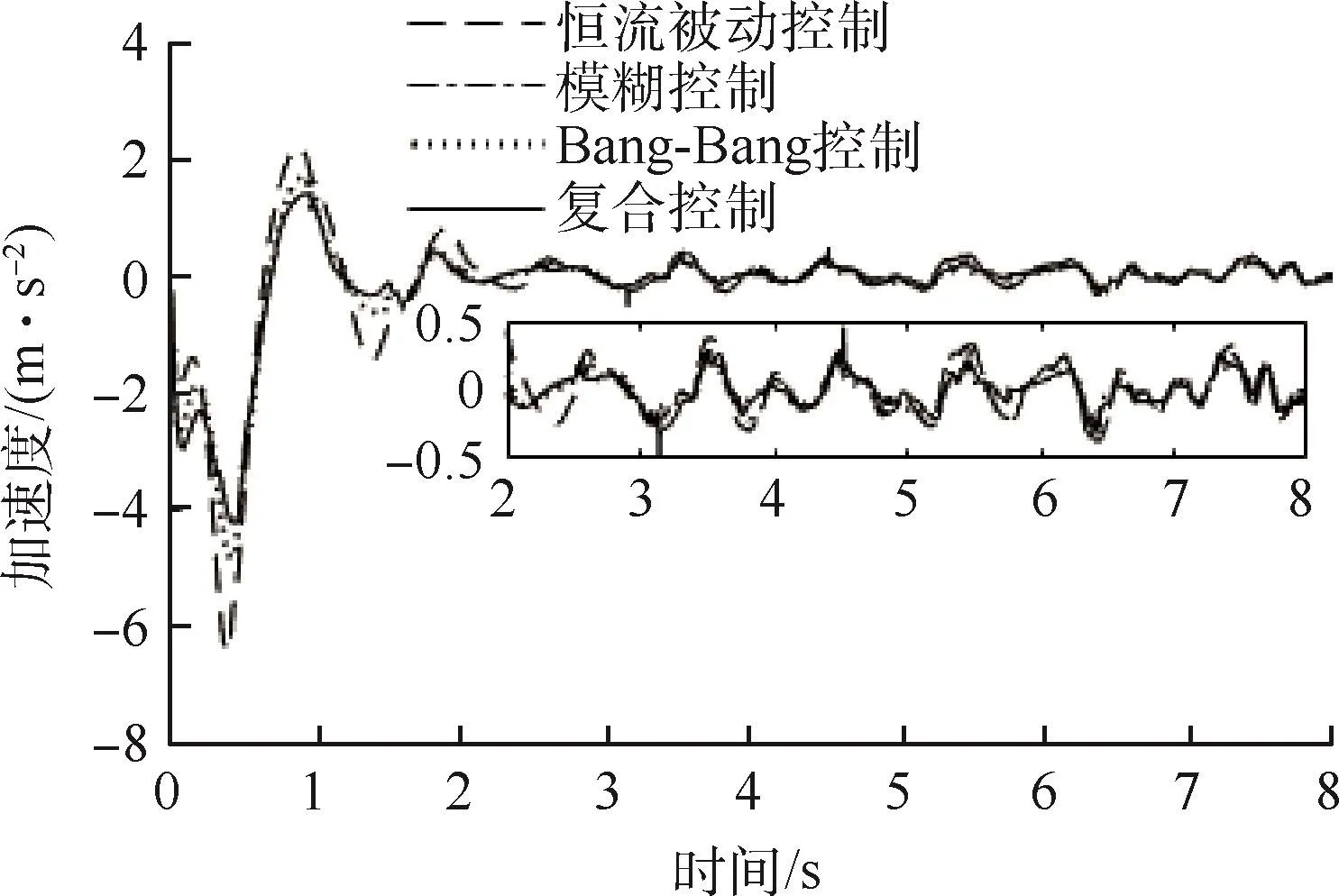
图11 加速度-时间
仿真结果可知,3种控制策略较恒流被动控制都有明显的性能提升,但3种控制策略的结果有所差异.模糊控制的模糊论域来源于对落震过程的专家库分析,Bang-Bang控制通常用来应对随机的噪声影响.在实际落震过程中,落震前期呈现规律振动,使用基于专家库分析的模糊控制会比Bang-Bang控制结果更好.而在落震后期,机体处于滑跑阶段,影响系统的主要因素是地面噪声,Bang-Bang控制可以尽快对无序噪声进行反映,较模糊控制有着更好的控制效果,而复合控制相当于在落震过程的前期与后期之间增加一个分离面,结合前二者优势以期获得更加优良的结果.

表4 仿真结果的均方根
4 结 论
以磁流变起落架为研究对象,对恒流被动控制、模糊控制、Bang-Bang控制与复合控制分别在落震速度为1.5 m/s的情况下进行仿真,通过分析磁流变减震器与起落架原理,进行磁流变减震器与起落架的动力学建模,并且采用Bang-Bang控制、模糊控制和复合控制策略比恒流被动控制加速度峰值分别降低34.70%、24.80%和34.70%,加速度均方差分别降低32.50%、26.80%和33.40%.模糊控制与Bang-Bang控制分别在落震阶段与滑跑阶段有较好的控制减震效果,但复合控制的综合控制效果最好.磁流变起落架动力学模型与这3种控制算法的研究为磁流变起落架的控制与结构设计提供理论基础.

