基于2体三维最大纠缠态的双向量子密集编码∗

赵雨曦 王 震 骆 磊

(1.辽宁师范大学物理与电子技术学院,辽宁 大连 116029;2.大连东软信息学院智能与电子工程学院,辽宁 大连 116023)

0 引 言

量子纠缠是量子力学最显著的特征之一,也是一种有用的量子资源,在量子计算和量子通信中起着重要的作用.基于2体二维体系最大纠缠态的量子通信技术被广泛应用于量子密钥分发[1-3]、量子隐形传态[4-6]、量子密集编码[7-8]、量子通信[9-10]等领域.

相对于二维量子位,高维量子位具有更大的信息容量,可以比量子比特荷载更多的信息.人们首先研究了高维量子位在量子密钥分发中的应用.2002年,Cerf等[11]在理论上提出利用d维量子态来实现量子密钥分发的理论方案,并证明了该方案的安全性;2007年,Khan等[12]提出利用多自由度光子来实现d维量子密钥分发并分析了该方案的实验可行性.近年来也有研究基于2体三维最大纠缠态的量子信息过程:2019年,Zhang等[13]提出利用辅助纠缠实现高维 Bell态的分析方法;同年,Luo等[14]在实验上实现了基于高维 Bell态的高维量子隐形传态.这些研究表明,高维量子位在量子信息过程中有着广泛的应用,但是针对高维最大量子纠缠态具体形式以及高维最大纠缠态的完备局域变换的种类,目前还没有具体给出.此外,高维量子纠缠态还可以应用在哪些量子信息过程中也没有具体的结论,这些都有待于进一步的研究.

本文以2体三维最大纠缠态为载体进行量子通信,利用文献[15-16]引入的符号法以及文献[17]给出的一般2体最大纠缠态的方法构造2体三维最大纠缠态,以及最大纠缠态的完备局域幺正算符集.在此基础上,通过改造量子密集编码方案,构造了双向量子密集编码的信息处理过程,并对通信过程的安全性进行了分析.

1 2体三维最大纠缠态

自1935年爱因斯坦等提出EPR佯谬之后,量子纠缠作为一种极具代表性的量子特性引起人们的注意,对量子纠缠的研究有助于更好地理解量子理论,拓广量子纠缠的应用.量子纠缠是对多子系统量子系统而言,当对其中1个子系统进行测量的同时,测量结果会影响另1个系统的状态,具有纠缠现象的量子系统的量子态称为纠缠态.纠缠态的定义较为复杂,对于2体纯态而言[18],其定义为:如果量子态|ψ〉12不能写成如下直积形式,|ψ〉12≠|α〉1⊗|β〉2(其中态|α〉1、|β〉2分别为子系统1、2的量子态),则|ψ〉12为2体纠缠态.

一般任意高维量子纠缠的结构还不是很清楚,但是对于确定维数的低维量子纠缠态形式和制备过程研究的较为清楚[19-20].本文取三维Hilbert空间的1组正交归一基矢量为{|1〉,|2〉,|3〉},由文献[17]可知,2体三维Bell态有9个,可以写成如下形式

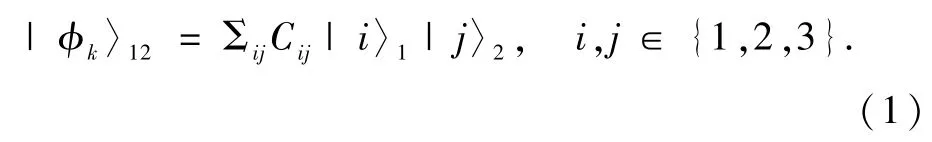
具体量子态可以表示为

式中ω为1的立方根,即ω3=1.容易验证,以上9个态也是2体三维系统的1组正交归一完备基.记作

对于2体纯态的量子纠缠度,一般采用部分熵纠缠度来衡量[21],其定义为

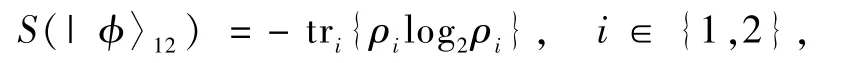
式中ρi=trj{|ϕ〉12〈ϕ|},i≠j∈{1,2}.由此容易计算出以上9个态部分熵均为

所以,以上9个态为2体三维最大纠缠态.针对以上9个纠缠态,相应的完备局域量子变换集为S={E0,E1,E2,E3,E4,E5,E6,E7,E8},各操作具体形式分别为

利用文献[17]方法容易验证,式(5)中任一操作,可以把式(2)中任意1个最大纠缠态唯一确定地变成另1个最大纠缠态(忽略态的整体因子).例如

因此可以对该操作进行编码,然后进行量子通信.对操作进行如下编码约定,即把式(5)中每个量子局域变换都对应为1个数字

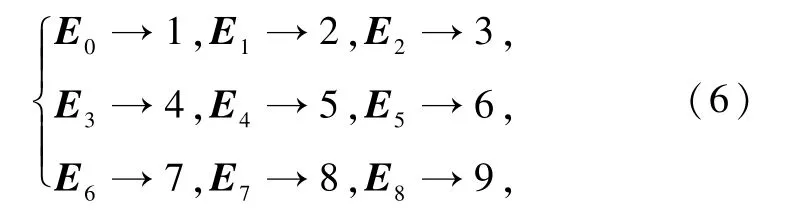
在式(6)编码的基础上进行通信.

2 具体方案

本文采用改进的双向密集编码方案,以|ϕ11〉12为例来说明该通信过程.具体操作如下:通信双方Alice和Bob分别拥有粒子1和粒子2,双方采取式(2)的纠缠完备基和式(5)的完备局域幺正操作集,根据式(6)的编码约定进行如下操作:

(1)Alice和Bob分享处于纠缠态|ϕ11〉12的粒子1和2.

(2)假定 Alice要把数字4发送给 Bob,同时Bob要把数字7发送给Alice.依据式(6),数字4编码为量子局域变换E3,数字7编码为量子局域变换E6.然后Alice对粒子1实施E3操作,记作

Bob要对粒子2实施E6操作,记作

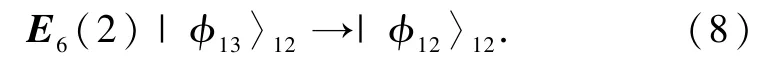
容易验证,Bob与 Alice的操作顺序不影响最后结果.

(3)Alice把粒子1发送给Bob,Bob对粒子1、2进行式(2)所示的2体三维Bell基测量,并公布测量结果;或者,Bob把粒子2发送给Alice,Alice进行相同的Bell基测量,并公布测量结果;也可以是Alice和Bob把粒子1、2发给一个共同的第三方Carl,Carl对粒子1、2根据式(2)所示的操作进行测量,并公布测量结果。这3种操作都可以完成量子通信过程,并且不影响该结果的安全性.

(4)Alice对照初始态|ϕ11〉12,最终态|ϕ12〉12以及自己的局域操作E3(1),可以唯一确定地知道Bob的局域操作E6(2);同样,Bob对照初始态|ϕ11〉12,最终态|ϕ12〉12以及自己的局域操作E6(2),可以唯一确定地知道Alice的局域操作E3(1).

具体解码方式可利用文献[17]中的符号,以及文献[22]中的类似公式给出整个通信过程的公式为

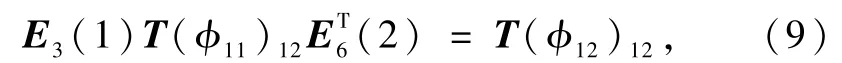
式中T(ϕ11)12、T(ϕ12)12分别为初始态|ϕ11〉12和最终态|ϕ12〉12的符号矩阵,上标T表示矩阵的转置.由上式可知,初始态与最终态是公开的信息,这样对于不知道Alice和Bob的局域操作,式(9)相当于1个二元一次方程

x与y是不可知的.但是对于Alice来说,对粒子1所实施的局域操作是可知的,此时方程(9)对于Alice而言就是1个一元一次方程,可以唯一确定Bob的局域操作

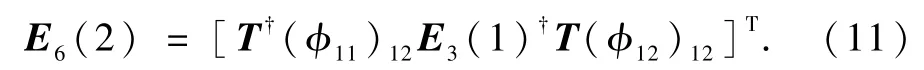
同样,对于Bob可以得到解码公式

式中†表示矩阵的复共轭.

3 安全性分析

在通信过程中,信息的安全性十分重要.依赖于纠缠的量子通信方案往往都要建立在纠缠粒子安全分享的基础上,利用文献[3]的操作很容易实现纠缠对的安全分享.所以,本文的讨论均基于纠缠通道已经安全建立的情况下,在其他可能的窃听攻击下,通信的安全问题.

如果在步骤(3)中Alice发给Bob的粒子1(或者Bob发给Alice的粒子2)被窃听者截获并替换,因为信息是编码在纠缠态|ϕ12〉12上的,窃听者并不能从单个粒子1(或粒子2)中获得通信双方局域操作信息.但这样做的后果会导致纠缠态|ϕ12〉12被破坏,形成一种类似截断通道的攻击,会被通信双方发现.

如果在步骤(3)通信双方把各自粒子发送给第三方时被窃听者全部截获替换,也就是窃听者获得最终态|ϕ12〉12,如果窃听者为了不被发现依旧正确公布测量结果,则通信过程依然成立,而由式(10)可知,窃听者依然无法知道通信双方的局域操作.因此,此通信过程是安全的.

4 结 论

量子密集编码信息是发送者通过1个粒子传递2个粒子荷载信息的单向通信过程,本文推广到基于2体三维最大纠缠态的双向通信过程,并构造了完备的2体三维最大纠缠态形式,给出了针对该最大纠缠态的完备局域操作元素.在此基础上,提出了基于2体三维最大纠缠态的双向量子密集编码方案,并分析指出该方案在安全分享了纠缠通道情况下是安全的.此方法也可以推广到更高维的情况.