一条中线长为整数的整边三角形
李 怡 朱一心 李克正
(首都师范大学数学科学学院,北京 100048)
0 引 言
三边长都为整数的三角形称为整边三角形.关于整边三角形的研究很多结论集中在满足特殊条件的三角形的存在性以及相应的计数问题上.常见条件是关于边的关系、角的关系、面积的关系,这些关系往往以某种定值问题出现.如:整边三角形的计数[1-2]、面积与周长数值相等的整边三角形计数[3-4]、有一个内角度数为60°或120°的整边三角形[5-6]等.
本文研究一条中线长为整数的整边三角形的存在和性质:整边三角形一条中线长为整数的充要条件;一条中线长为整数的一类特殊的整边三角形.
本文有关的符号说明:
(1)用a、b和c分别表示△ABC3个内角∠A、∠B和∠C的对应边;
(2)用三元无序实数对表示三角形的3条边长,例如(12、5和13)表示边长分别为12、5和13的三角形,称为整边三角形(12、5和13);
(3)N+,Z表示正整数和整数集合.
1 主要结果及证明
定理1 设整边三角形的3条边分别为a、b和c,边a上的中线长是整数的充要条件是2b2+2c2-a2为偶平方数.
(注:由于整边三角形的3条边满足b+c>a,易知2b2+2c2-a2≠0.)
证明如图1所示,△ABC是整边三角形,3边分别为a、b、c,设D是BC的中点,BD=CD=t,点A到对边a的中线长为z,需证:z为整数当且仅当2b2+2c2-a2为偶数的平方,且2b2+2c2-a2≠0.
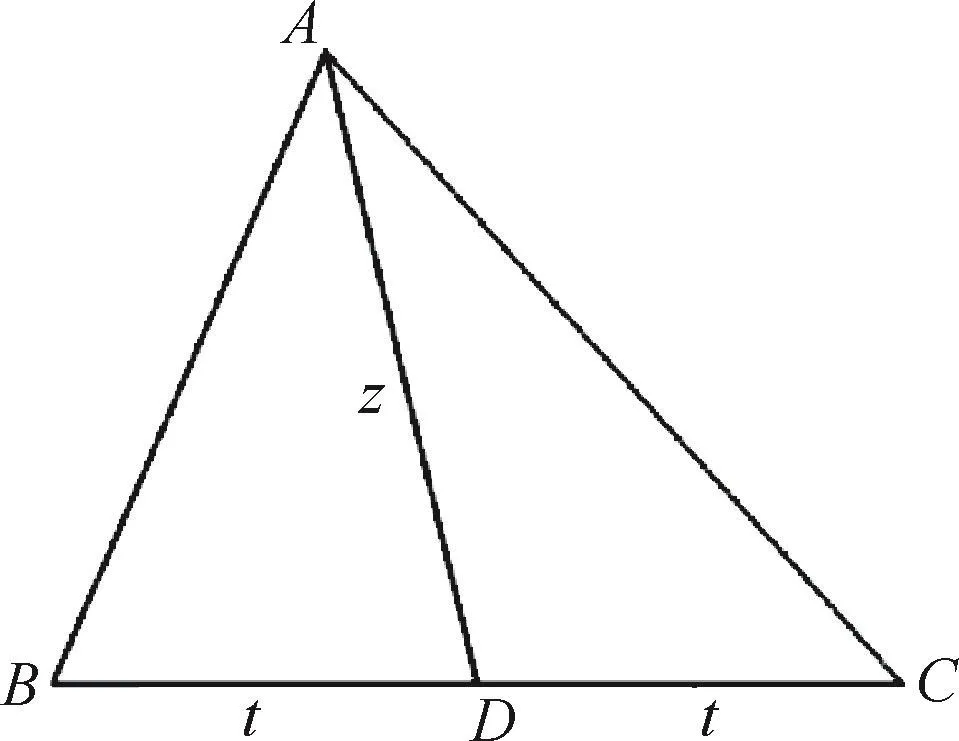
图1 整边三角形

一条中线长为整数的整边三角形是否存在,需要知道中线长为整数的整边三角形的三边性质.
推论整边三角形1条边中线长为整数的必要条件是该边长必是偶数,另外2条边长同奇偶.
证明若边a上的中线长为整数,由定理1可知,2b2+2c2-a2是正的偶平方数.设2b2+2c2-a2=(2n)2,n是正整数,则a必为偶数,设a=2k,k∈N+,有b2+c2=2k2+2n2,则b、c同奇偶.
从证明可知,求出不定方程b2+c2=2k2+2n2的整数解,便可得到边a上的中线长为整数时,整边三角形3边的表示.因此要求不定方程
b2+c2=2k2+2n2(∗)
的整数解,其中b,c,k,n∈N+;b、c同奇偶.
为此,先回顾一些抽象代数知识[7]:
(1)形如Z[i]={a+bi|a,b∈Z}的复数关于数的加法和乘法构成一个整环,称为高斯整数环.Z[i]是唯一分解整环.Z[i]中的单位:-1,1,-i,i.设p是整环D的1个非零非单位的元素,如果对任意的a,b∈D,由p整除ab,可推出p整除a或p整除b,则称p为D的1个素元.
(2)设α=a+bi∈Z[i],定义ф(α)=a2+b2为Z[i]中元素α的范数.
(3)对于Z[i]中的整数元素p,若方程x2+y2=p没有整数解,则p是素元;对于Z[i]中的非整数元素α=a+bi,若ф(α)为素数,则α为素元.
下面解不定方程(∗):
解利用高斯整环Z[i]是唯一分解整环这一事实,将方程(∗)在Z[i]中分解,得:

因为ф(1+i)=ф(1-i)=2,所以1+i,1-i都是Z[i]中的素元.不妨设(1+i)整除(b+ci),取共轭可知(1-i)整除(b-ci).
令gcd(b+ci,k+ni)=p+qi∈Z[i],p,q∈N+,则存在u+vi∈Z[i],u,v∈N+,使得
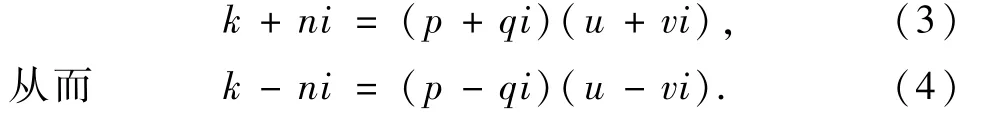
注意到gcd(b+ci,u+vi)=1(否则与gcd(b+ci,k+ni)=p+qi矛盾),结合式(4)可知,(u+vi)整除(b-ci),从而(u-vi)整除(b+ci).
由上所述有
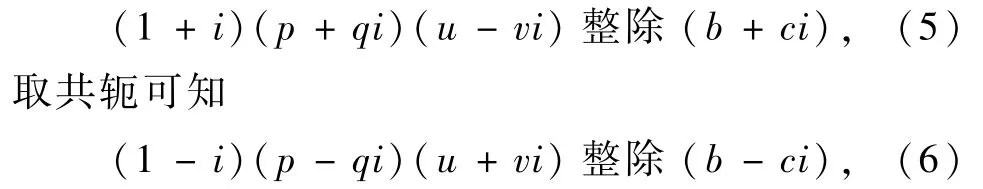
将式(3)、式(4)代入式(2),得:
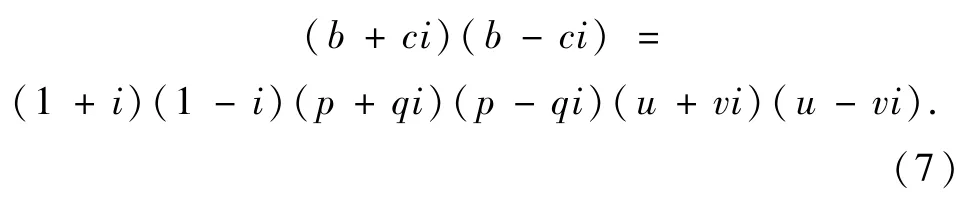
考虑到Z[i]中的单位有±1,±i,结合式(5)、式(6)、式(7)可得:


展开式(10)、式(11),并使等号两边虚、实部分别相等,得到不定方程(∗)的4组解:

式中p,q,u,v∈Z.
由不定方程(∗)的解可得如下定理:
定理2不定方程b2+c2=2k2+2n2的解为①~④.
由此可以讨论边a上的中线长为整数的整边三角形3条边的表示.
由于①~④中k的表示相同,所以a=2k=2pu-2qv.为了讨论方便,假设p、q、u、v都是非负整数.在分析时要注意三角形3条边长需要满足a+b>c,b+c>a,c+a>b.
i)对于解①:
因为a+b=(2pu-2qv)+(pu-qu+pv+qv)=3pu-qu+pv-qv,所以a+b-c=(3pu-qu+pv-qv)-(pu+qu-pv+qv)=2pu-2qu+2pv-2qv=2(p-q)(u+v)>0,则需要p-q>0,即p>q;
因为b+c=(pu-qu+pv+qv)+(pu+qupv+qv)=2(pu+qv),所以b+c-a=2(pu+qv)-(2pu-2qv)=4qv>0,满足b+c>a;
因为c+a=(pu+qu-pv+qv)+(2pu-2qv)=3pu+qu-pv-qv,所以c+a-b=(3pu+qu-pv-qv)-(pu-qu+pv+qv)=2pu+2qu-2pv-2qv=2(p+q)(u-v)>0,则需要u-v>0,即u>v.
所以,若p>q,u>v,且p、q、u、v都是非负整数,那么得到的a、b和c能构成三角形.再来看在这样的条件下,是否能使a、b和c都是正数:
因为pu>qv,所以a=2pu-2qv>0;
因为p>q,则b=pu-qu+pv+qv>pupu+pv+qv=pv+qv>0;
因为u>v,则c=pu+qu-pv+qv>pu+qu-pu+qv=qu+qv>0.
综上所述:在p>q,u>v,且p、q、u、v都是非负整数的条件下,由解①得到的a、b和c可以构成三角形.
那么此时是否满足b、c同奇偶的要求.将解①中b、c的表示写为:b=(pu+qv)+(pv-qu),c=(pu+qv)-(pv-qu).根据一般性的结论:对于2个整数x、y、x+y和x-y同奇偶.所以可知解①中的b,c同奇偶.
ii)对于解②:
注意到p、q、u、v都是非负整数,则b+c=(-pu+qu-pv-qv)+(-pu-qu+pv-qv)=-2(pu+qv)<0,与b+c>0矛盾,所以无解.
iii)对于解③:
a+b=(2pu-2qv)+(-pu-qu+pv-qv)=pu-qu+pv-3qv,注意到p、q、u、v都是非负整数,所以a+b-c=(pu-qu+pv-3qv)-(pu-qu+pv+qv)=-4qv<0,与a+b>c矛盾,所以无解.
iv)对于解④:
a+c=(2pu-2qv)+(-pu+qu-pv-qv)=pu+qu-pv-3qv,注意到p、q、u、v都是非负整数,a+c-b=(pu+qu-pv-3qv)-(pu+qu-pv+qv)=-4qv<0,与a+c>b矛盾,所以无解.
因此得到:
定理3任取p,q,u,v∈N+;p>q,u>v,当a=2pu-2qv,b=pu-qu+pv+qv,c=pu+qupv+qv时,三角形(a、b、c)是1条中线长为整数的整边三角形.
2 例 子
以下例子说明如何利用定理3求得1个1条中线长为整数的整边三角形:
例根据定理3,取p=3,q=2,u=2,v=1,计算得到a=8,b=7,c=9,可以验证a上的中线长为7.
由于在定理 3中假设了p、q、u、v都是非负整数,因此并不是将不定方程的所有解都对应到得到的中线长为整数的整边三角形,只是得到其中一部分.

