具有时滞的非线性二阶多智能体系统群组一致性
张丽琼,李伟勋,刘 佳
(1.天津职业技术师范大学理学院,天津 300222;2.天津职业技术师范大学自动化与电气工程学院,天津 300222)
多智能体系统(multi-agent system,MAS)是由多个智能体组成,将大而复杂的系统建设成小的、彼此互相通信并协调的、易于管理的系统。近年来多智能体系统已经应用于人类生活的方方面面,如无人驾驶机器、分布式机器人通信、机器人编队、交通运输、蜂拥现象、复杂神经网络和电脑通信等,原理都是通过设计合理的算法和控制协议,让各个智能体之间互相通信,从而使多智能体的各个状态趋于一致[1-10]。Dong等[1]研究了在切换拓扑和时变的情况下,二阶多智能体系统的编队跟踪及其在四旋翼编队飞行中的应用。Tang等[2]研究的是脉冲新特征下,网络多智能体系统的跟踪控制及其在机器人系统中的应用,为机器人的发展提供了一个崭新的前进方向。Li等[3]研究了二阶多智能体系统量化蜂拥控制。He等[4]对无线传感器网络中基于共识的时间同步做了研究,这是对复杂网络的研究。Wang等[5]分别在固定和切换拓扑结构下,研究了具有多智能体系统领导跟随的编队控制。Jadbabaie等[6]提出了在多智能体系统的研究中使用最近邻规则的移动自治智能体组的协调,为研究多智能体系统一致性提供了新思路。研究发现,时滞对多智能体系统一致性的影响及其广泛,文献[7-9]考虑了在具有时变通信时滞下多智能体系统的一致性问题,与实际工程问题相符。此外,一旦涉及实际问题,人们往往希望系统能够在较短时间内完成任务。Wang等[10]就是在有限时间内对多智能体系统的一致性问题进行研究,因此多智能体系统能够快速有效地解决实际工程问题,表明了多智能体系统在社会生活中的重要地位。
多智能体系统的组一致性研究作为一个分支得到了广泛关注。组一致性是指在整个多智能体系统中,系统会因为环境状况等因素,出现收敛成多个稳定状态的现象,也是各个智能体达到各自所在组的一致状态。Yu等[11]首次研究具有切换拓扑和通信延迟的多智能体系统的组一致性的概念。2年后,Yu等[12]对具有向信息交换的多智能体系统的群共识进行了研究。Xie等[13]得到了多智能体系统组一致性的充分必要条件。学者对多智能体系统的组一致性进行了诸多研究,Wen等[14]关于具有输入饱和的异构多智能体系统的群体共识问题进行了研究。Feng等[15]考虑了双积分器动态多智能体系统在固定通信拓扑下的群组一致性控制。在理论与实际相结合时,群组一致性的研究具有重要的意义。本文在已有结论的基础上,研究多智能体系统的三组一致性问题。
1 基础知识和模型阐述
1.1 代数图论
把多智能体系统的通信拓扑建模成有向图。图的基本概念如下:
令G=(N,T,A)是一个拓扑图,其中一个非空的有限集 N={n1,n2,…,nm}叫做 G 的顶点集,N 中的元素称为顶点;集合T⊂N×N为G的有向边,可以用{ej,ei}来表示;A=[aij]m×m是 G 的一个加权邻接矩阵。如果{ej,ei}∈T,则 aij≠0 表示第 i个智能体能够接收到第j个智能体的信息,否则aij=0;另外假设所有aii=0,用={nj∈N:(nj,ni)∈T}表示节点i的邻居节点的集合。有向图G的拉普拉斯矩阵L定义为L=(lij)m×m,且计算式为L=D-A,其中,矩阵D为图的度矩阵,节点的入度矩阵用in-degree表示,且定义为degin(vi)=节点的出度矩阵表示为out-degree,定义为
1.2 问题描述
考虑m个智能体,假设所有智能体是同质的,且智能体的状态都属于状态空间R,则
智能体i的动力系统模型为
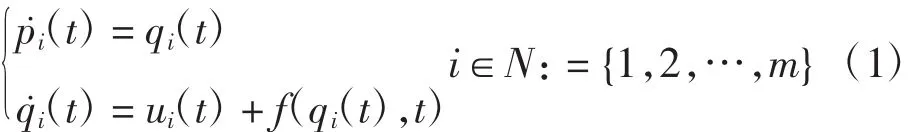
式中:pi∈R和qi∈R分别为表智能体系统的位置状态和速度状态;ui∈R为系统的控制输入;f(qi(t),t)为连续可微向量函数。
领导者的动态模型为
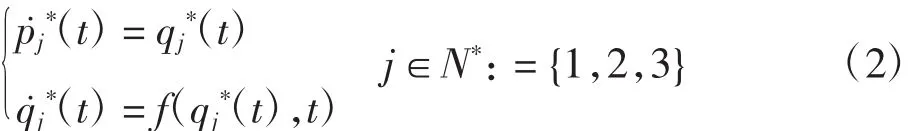
式中:pj*∈R和qj*∈R分别为领导者的位置状态和速度状态;f(qj*(t),t)为连续可微向量函数。
本文是在一维环境下考虑多智能体系统的组一致性,也可以通过Kronecker积将结果推广到高维空间,这将是以后要研究的重点问题。为了让所有智能体与它所跟随的领导者达成一致,设计如下控制协议
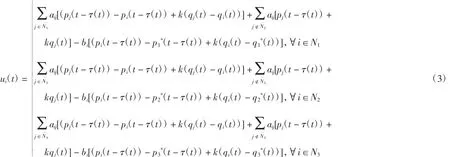
定义1在任意初始条件下,若多智能体系统满足以下式子
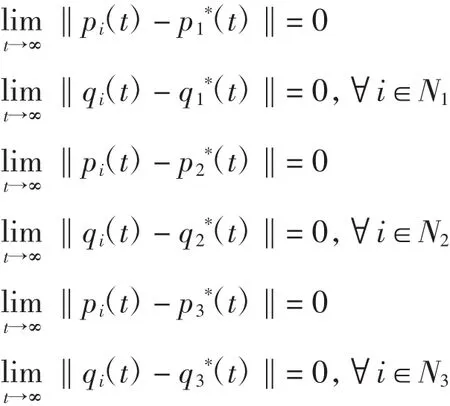
则称多智能体系统能够达到三组一致性。
引理1文献[12]在连通的拓扑图中,每个节点与其他各个子组中节点的权重之和为0,如下式

假设1文献[5]非线性动态f(qi(t),t),f(qj*(t),t)是连续可微的向量函数,则存在一个正常数ρ使得以下不等式成立

引理2文献[5](Schur补引理)矩阵s11,s12为对称阵且,则下列条件相互等价
(1)S< 0
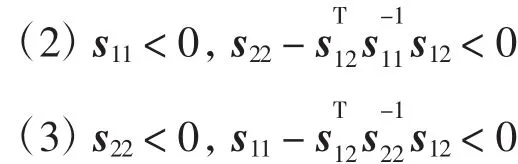
引理3文献[15]对任意向量a、b和一个正定矩阵Φ,有以下式子成立
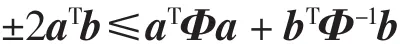
2 主要结论
根据控制协议(3)和上述的引理1,则系统(1)可以写成下面的矩阵形式

式中:F(q(t),t)=(f(q1(t),t),f(q2(t),t),…,f(qm(t),t))T;p(t)=(p1(t),p2(t),…,pm(t))T;q(t)=(q1(t),q2(t),…,qm(t))T;p*(t)=(p1*(t),p2*(t),p3*(t))T;q*(t)=(q1*(t),q2*(t),q3*(t))T。
由上述智能体的动力系统和领导者的动力系统,可以得出误差系统的动力模型。
令ξi(t)=pi(t)-p1*(t),ηi(t)=qi(t)-q1*(t),(i∈N1);ξi(t)=pi(t)-p2*(t),ηi(t)=qi(t)-q2*(t),(i∈N2);ξi(t)=pi(t)-p3*(t),ηi(t)=qi(t)-q3*(t),(i∈N3);ξ(t)=[ξ1(t),…,ξm(t)]T,η(t)=[η1(t),…,ηm(t)]T,则误差系统的矩阵形式如下
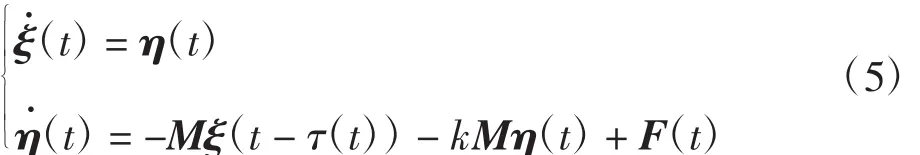
式中:F(t)=(f1(t),f2(t),…,fm(t))T,且fi(t)=(f(qi(t),t)-f(qj*(t),t);L+B=M。
基于多智能体系统和上述的误差系统,定义新的
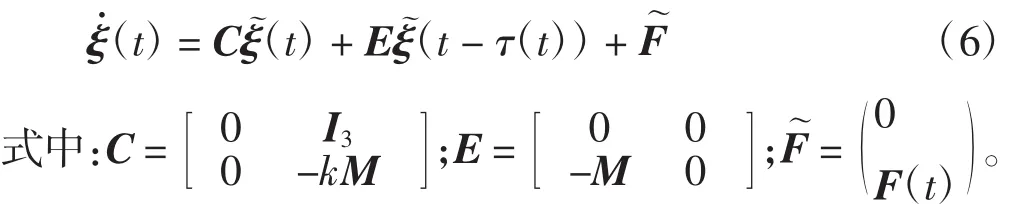
定理1针对非线性多智能体系统(1)和(2),在控制协议(3)的作用下,若对于给定的正常数 τM、δ、ρ,存在正定矩阵P、Q、R满足以下的不等式


则多智能体系统是能够达到群组一致性的。
证明针对系统(6),建立一个Lyapunov候选泛函数为



根据牛顿莱布尼兹公式,可得
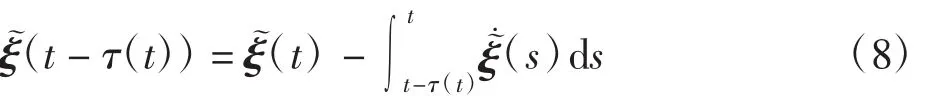
则系统(6)可表示为

式中:N=C+E。
再对Vi(t)进行求导,得
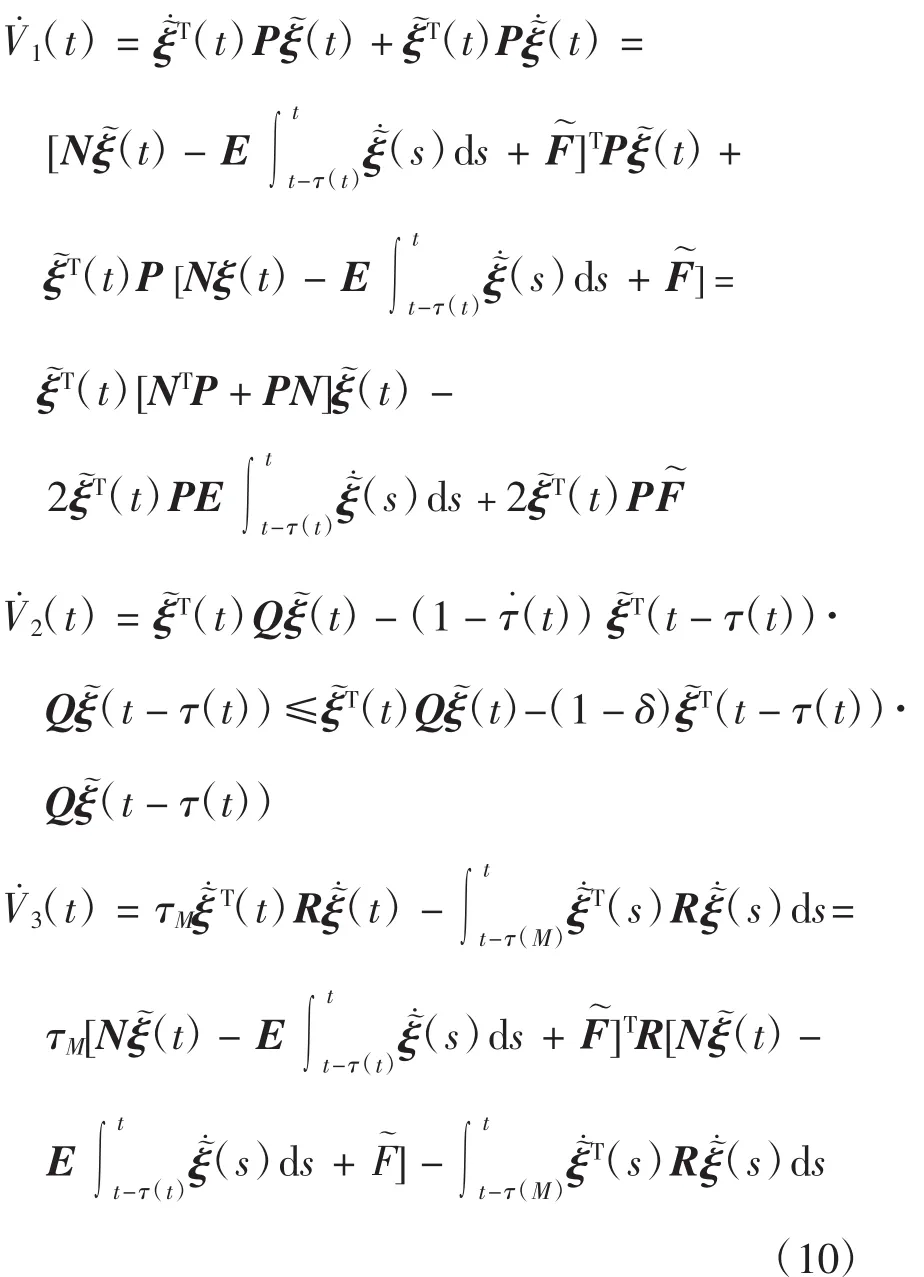
根据式(10)和假设并整理,可以得到下式
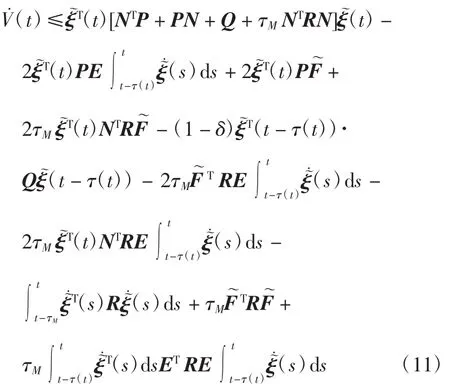
由引理3可将式(11)整理为
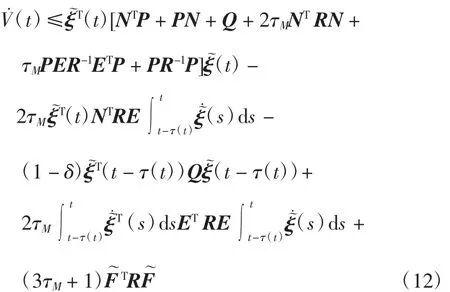
再由假设1可将式(12)处理为如下不等式
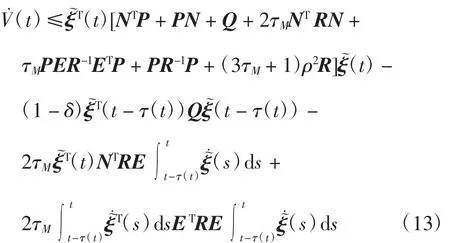
再根据式(8)可以得到不等式

由Lyapunov稳定性理论,可知误差系统(6)能够趋于稳定,即等价于该系统达到了群组一致,证毕。
特别地,若时滞为0时,仍然可借助Lyapunov稳定性理论和线性矩阵不等式等工具,通过运用Schur补引理等相关的引理,实现多智能体系统的群组一致性,基于邻居的运动状态设计如下算法
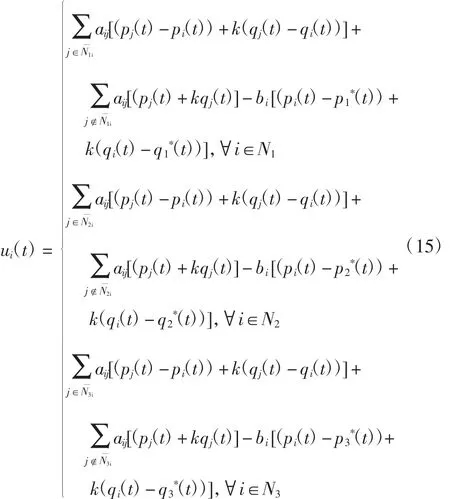
推论1针对非线性多智能体系统(1)和(2),根据控制协议(15),对于给定的正常数,要使多智能体系统实现群组一致性,则需存在正定矩阵,满足以下线性矩阵不等式
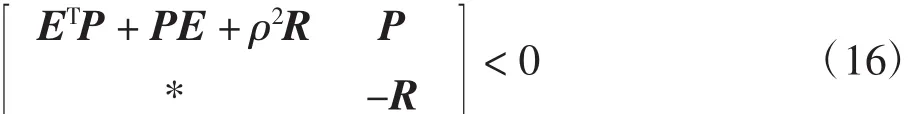
3 数值模拟
为了进一步展现结果的有效性,运用数学工具对多智能体系统进行仿真模拟,该系统的所有智能体共分为3组,每组都有一个领导者,每一区域表示一组,组与组之间用黑色的有向箭头连接,有向的拓扑结构如图1所示。
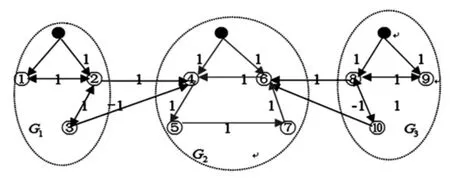
图1 有向的拓扑结构
取增益常数,按照上述的有向拓扑结构图给出非线性动力系统无时滞时的位置误差轨迹和速度误差轨迹分别如图2和图3所示。在有时滞的条件下,系统的位置误差轨迹和速度误差轨迹分别如图4和图5所示。
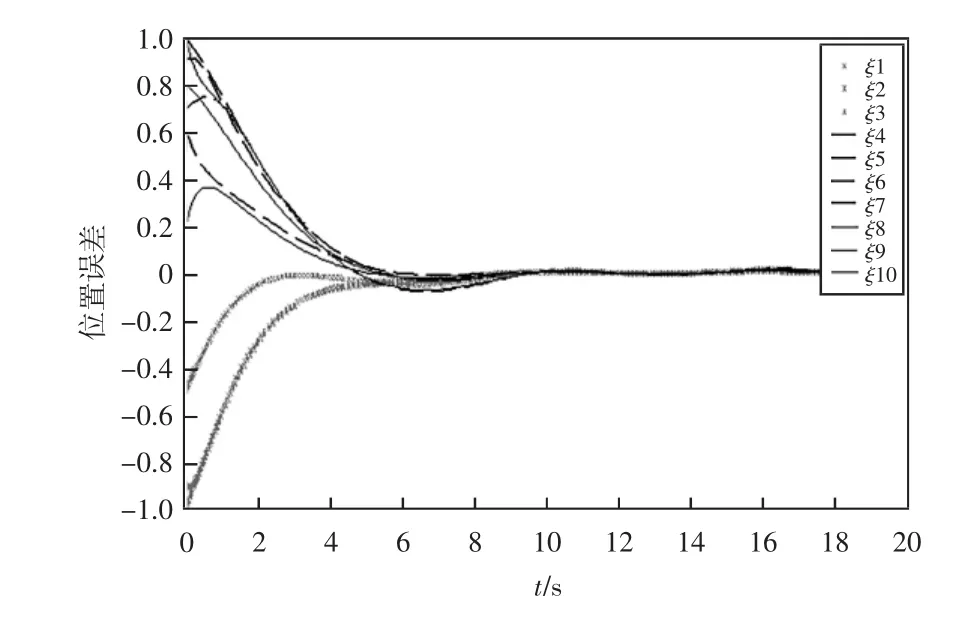
图2 无时滞时的位置误差轨迹
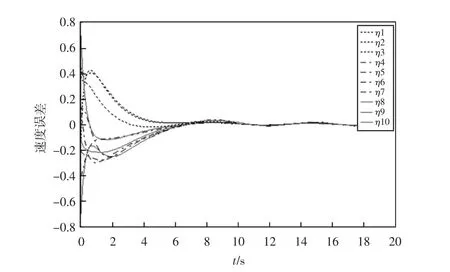
图3 无时滞时的速度误差轨迹

图4 有时滞时的位置误差轨迹
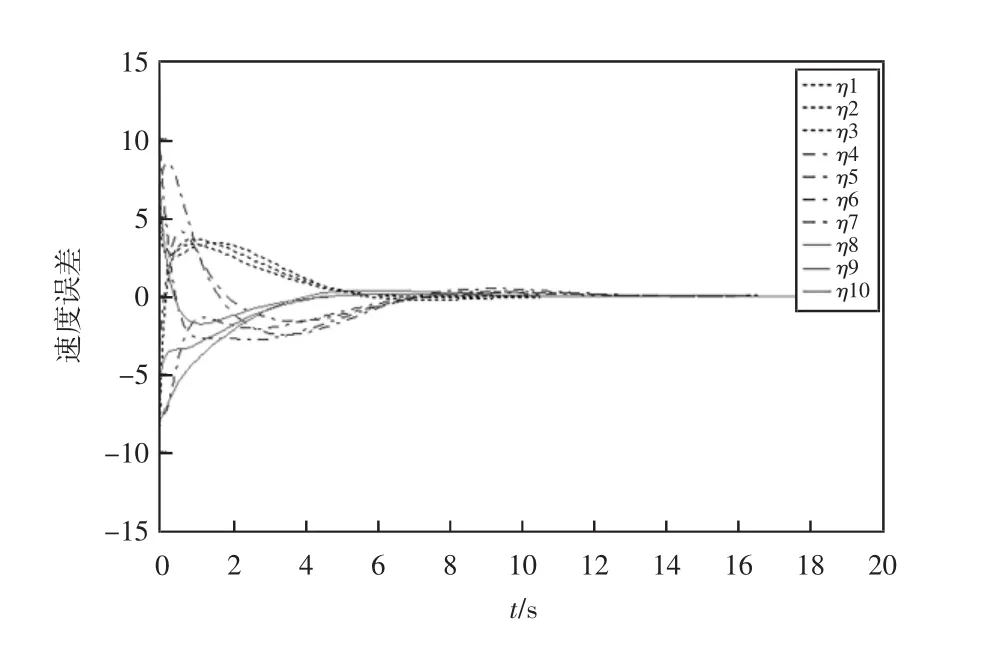
图5 有时滞时的速度误差轨迹
从图2和图3可以看出,二阶非线性多智能体系统在无时滞的情况下,其跟随者的位置和速度与领导者的位置与速度之间的误差曲线趋于0,同时也说明了该系统实现了组一致性;从图3和图4可以看出,智能体与领导者之间的误差也趋于0,即多智能体系统在有时滞的影响下也能够实现组一致性。
(1)无时滞非线性多智能体系统的群组一致性
假设智能体的初始状态为:[-1.0,-0.9,-0.5,0.6,0.9,1.0,0.7,0.8,0.2,1.0,0.5,-0.3,0.4,-0.4,0.2,-0.2,0.1,-0.1,0.8,-0.8]。
(2)有时滞非线性多智能体系统的群组一致性
假设智能体的初始状态为:[-10,-9,-11,12,9,1,-1,8,2,10,6,-12,7,-4,11,-4,6,-7,9,-8]。
4 结语
本文设计了分布式领导跟随控制协议,运用Lyapunov稳定性理论和线性矩阵不等式分别给出了连续时间多智能体系统在有通信时滞和通信时滞为0的2种情形下能够实现3组一致性的充分条件。为了能让理论成果得到进一步的论证,采用Matlab数学软件对结果进行了数值模拟,通过仿真图可以看到多智能体系统在控制协议下误差的各个状态均趋于0,说明多智能体系统实现了组一致性。

