面向有向网络关键节点识别算法研究

宁 阳，武志峰，宁 晴

（1.天津职业技术师范大学信息技术工程学院，天津 300222；2.北京联合大学信息服务工程重点实验室，北京 100101）

关键节点识别算法的研究在医学、社会学、网络安全、电力交通、政治与经济学等领域有重要意义，是复杂网络中重要的研究课题之一，是近年来国内外学者研究的重点问题。如在社会网络中通过挖掘关键节点控制流言的传播，疾病传播过程中挖掘关键节点控制疾病的蔓延，电力交通网络中识别关键枢纽进行重点维护，科学引文网络中通过挖掘关键节点找到学科带头人，互联网络中根据关键节点进行页面排序等，这些都可以降低经济成本，保证正常运行[1]。在考虑有向网络中的节点重要性时可以简单地将有向网络视为无向网络，利用无向网络中的节点重要性指标进行识别，但是这种方法忽略了节点之间的方向性[2]。考虑节点的方向性，Page等[3]提出的算法是有向网络中节点重要性排序的经典算法之一，网页链接向节点的出度节点进行转移，使整个网络的概率转移达到平稳状态，但是存在节点出度为0的悬挂节点和参数不确定问题；Kleinberg[4]提出的HITS算法考虑用节点的权威值（authority）和枢纽值（hub）的指标衡量节点重要性，但是没有在实际的搜索引擎中广泛应用；LYU等[5]提出的LeaderRank算法通过添加虚拟背景节点与网络中所有节点双向连接，解决PageRank算法的悬挂节点和消除参数影响的问题，但仍存在计算复杂度高的问题；Wang等[6]提出的 Pro-PageRank 和 Liu 等[7]提出的DPRank方法考虑了入度（出度）节点的邻居节点信息，前者倾向于向入度节点更大的节点方向转移，后者考虑倾向于向出度大的节点转移，改进了PageRank算法，但是仍存在悬挂节点需要以等概率向任意节点跳转的参数问题；宋琛等[8]提出的叠加随机游走计算相似和衡量节点重要性的方法能够有效地在无向网络中进行关键节点识别，但该方法没有考虑节点间概率转移的倾向问题，也没有解决如何在有向网络中进行关键节点识别的问题。本文基于Jaccard拓展指标[9]改进叠加随机游走方法，提出解决有向网络中传统关键节点识别方法的参数问题，以期更有效地在有向网络中进行关键节点的识别。

1 相关概念

1.1 网络表示

将一个具体网络抽象为一个由点集V和边集E组成的图G=（V，E）。顶点数记为N=|V|，边数记为M=|E|。有向无权图G的邻接矩阵A=（aij）N×N是一个N阶方阵，第i行第j列上的元素aij定义如下：

有向网络中节点i的度包括出度和入度，节点i的出度kiout（kiin）表示节点i指向其他节点（其他节点指向节点 i）的边的数目[2]，即

1.2 相关算法

PageRank是一种对网页按重要性进行排序的方法，如果一个页面被很多高质量页面指向，那么该网页的质量也很高，即一个节点被很多概率比较大的节点指向，那么通过某个节点到达这个节点的概率也越高。为了解决悬挂节点问题，PageRank算法中每一个节点都会以一定的概率跳转到网络中的任一节点，经过不断迭代，每个节点的PageRank值将趋于稳定。

式中：Pi（tn）为节点i第tn步的PageRank值；N为节点个数；1-c为跳转概率，也称阻尼系数，通常c=0.85。

文献[5]通过添加一个虚拟的背景节点g，使其与网络中所有节点两两双向连接，解决出度为0的悬挂节点问题，当迭代达到稳定，将虚拟背景节点的权值平均分配给每一个节点，以此来衡量节点重要性，该指标值越大，节点越重要。

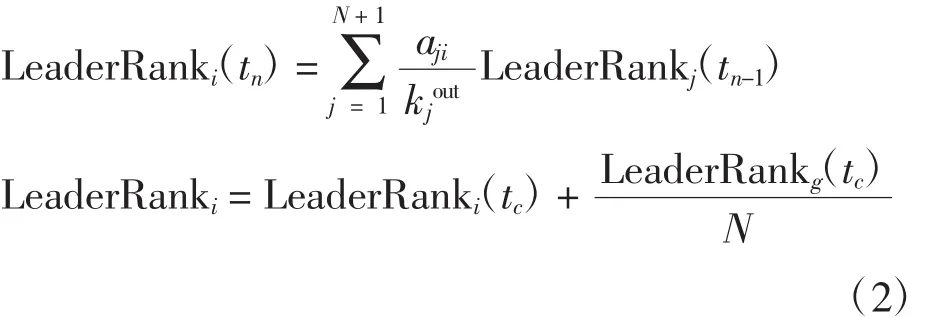
式中：LeaderRanki（tn）为节点i第tn步的LeaderRank值；tc为稳态时刻；LeaderRanki为节点 i最终LeaderRank值。

文献[6]提出一种改进的Pro-PageRank方法，节点在转移过程中更倾向沿着权重大的边游走，边的权重通过出度节点的入度邻居信息衡量，即节点更倾向于沿着入度大的节点进行转移。

式中：p（j，i）为节点j向节点i转移的概率；Γout（j）为节点j的出度邻居节点集合，即节点j指向的节点集合；Γin（i）为节点i的入度邻居节点集合，即指向节点i的节点的集合；Pro-PageRanki（tn）为节点i第tn步的Pro-PageRank值。

文献[7]考虑两步转移节点信息，节点更倾向于度（出度）大的节点转移，提出适用于有无向网络（有向网络）的DPRank关键点识别方法，无向网络中通过转移概率矩阵的转置计算最大特征值1对应的特征向量衡量节点重要性，有向网络通过迭代计算可通过达到平稳分布时节点的DPRank值衡量节点重要性。值得注意的是有向网络中仍存在出度节点的出度和为0的悬挂节点，即两步转移没有可达节点的情况，此时以1/n的概率跳转到任一节点。DPRank方法构建的转移概率矩阵为

式中：kj为无向网络中节点的度；Γ（i）为节点i的邻居节点集合；Pij为转移概率矩阵第i行第j列的值。

2 扩展Jaccard指标关键节点识别算法

2.1 扩展Jaccard指标构建转移概率矩阵

随机游走指基于过去的表现，无法预测将来的发展步骤和方向，下一步的选择是随机的。一般来讲，节点通过存在边到达相邻节点的概率是相同的，到达非邻居节点的概率是0，即等概率随机选择到达存在边的节点。但实际中，从一个节点到其他邻居节点的概率并不均匀随机，而是有偏的，所以本文采用扩展的Jaccard指标衡量有向网络中节点之间的相似性，考虑局部范围内的节点信息。对于2节点之间是否存在直接连边进行分别处理，从而进行确定转移概率矩阵。

Jaccard指数

式中：sij为节点 vi、vj的相似性。

Jaccard指数扩展到有向网络得到扩展指标，采用分母加1处理分母为0的情况。

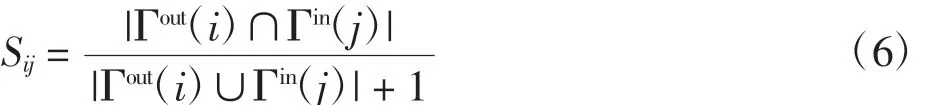
有向网络中2节点直接相连，若计算出Sij为0，则采用基于相似和的叠加随机游走的方法节点出度分之1弥补扩展Jaccard指标计算不足的问题；无论节点之间是否直接相连，节点倾向于向相似度小的节点方向转移，以寻找足够少、差异较大、能够覆盖整个网络的节点，但在2节点之间无直接连边，计算出Sij为0的情况下，节点之间的转移概率为0。

式中：Sij为扩展后用于衡量有向网络节点相似性的指标。

通过概率标准化处理，得到转移概率矩阵。上述相似性指标标准化处理，使转移概率矩阵中各行元素之和均为1。

式中：pij为概率矩阵中的元素为概率标准化后对应位置的值。

2.2 基于相似和的叠加随机游走

Liu等[10]考虑有限次的随机游走，提出一种基于网络局部随机游走的相似性指标（LRW），在LRW基础上，将t步及其以前的结果加和得到SRW的值，即

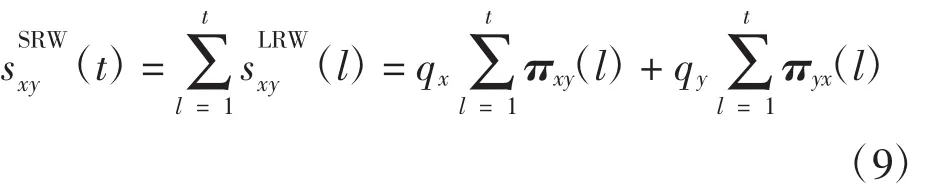
设各个节点的初始资源分布为qx，基于t步随机游走的相似性为

利用一种与度分布一致性的初始资源qx=kx/M，M作为网络的总边数，对每一对节点对都相同，计算过程忽略不计。πyx（t）为walker从节点x经过t步游走到节点y的转移概率矩阵，一般的k步转移概率矩阵正好是一步转移概率矩阵的k次方，可以证明k步转移概率矩阵中各行元素之和都是1。

相似度矩阵中的值代表对应节点之间的相似度，每一行代表当前节点与其他所有节点的相似度，采用文献[8]提出的相似和概念衡量节点重要性。累加各行相似度，得到基于相似和的叠加随机游走相似性指标，并将其标准化处理，将其用作网络中关键节点识别。

算法步骤：

①将有向网络表示为邻接矩阵的形式；

②根据扩展的Jaccard指数计算转移概率矩阵；

③使用叠加随机游走相似和方法衡量节点重要性值；

④利用节点重要性最大值进行标准化处理。

3 实验分析

3.1 评价指标

3.1.1 SIR传播模型

本文使用SIR传播模型[2，11]得到的排序作为标准排序结果，在典型的传染病模型中，N个节点的状态可分为如下3类。

S：易染状态，初始条件下所有节点均为易染状态，该节点以β的概率被邻居节点感染。

I：感染状态，感染某种病毒作为传染源的节点，该个体以β概率感染其邻居节点。

R：移除状态，也称免疫状态或恢复状态，感染状态节点以β概率感染邻居易感节点后，以γ概率变为移除状态R，不再具有感染能力和易感特性。

采用单源感染模型，初始时刻，假设网络中只有一个节点处于感染状态，其余个体均处于易感状态，一个单位时间内，所有处于感染状态的节点以β=的概率感染其周围邻居节点，之后以γ=1的概率变为移除状态，统计达到稳定状态时，即不存在易感节点，统计处于移除状态节点的个数，用于衡量初始感染状态节点的传播能力。为减少β、γ参数带来的随机性，每个节点计算100次，利用平均值进行计算。对网络中所有节点均执行相同操作，根据节点的传播能力得到网络中节点重要度排序。其中，＜k＞为平均度，＜k2＞为平均度方。

3.1.2 Kendall tau距离

Kendall tau距离[12-13]计算2个排序列表之间成对分歧数量，即2个列表σ和τ，K（σ，τ）表示2个列表之间的差异性

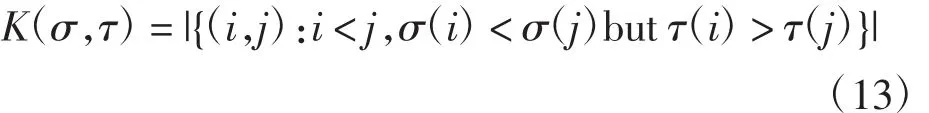
K∈[0，1]，K 值越大，相似性越小。Kendall距离归一化处理得，将其用于比较一个序列与另一个类似标准答案的排序序列的相似性，得出排序序列有效性，K′值越大，2个列表之间相似性越大。σ列表与τ列表计算Kendall tau距离相似值的过程如表1所示。

表1 σ列表与τ列表计算Kendall tau距离相似值的过程

表中分别列出列表的所有二元组组合，当σ（i）＜σ（j）且 τ（i）＞ τ（j）或者 σ（i）＞ σ（j）且 τ（i）＜ τ（j）时，K=1，否则 K=0。

例：σ ={1，2，3，4}，τ={1，3，2，4}

由表 1可知，K 的值为 1，K′=1-2*1/4*3=0.833。

3.2 实验结果与分析

根据上述分析，为了验证本文提出方法的有效性及准确性，设计2组对比实验，在2个网络数据集进行仿真实验，并与 PageRank（PR）、Pro-PageRank（Pro-PR）、LeaderRank（LR）、DPRank（DPR）算法指标进行对比分析，验证算法的有效性；使用SIR传播模型计算标准排序结果，计算各中心性算法与SIR的Kendall tau相关系数，验证算法的准确性。

Freemans_EIES_3[14]网络是从事社会网络分析与研究之间关系的网络，包含32个节点，442条有向边，节点平均度 27.625，SIR传播模型感染概率 β为0.029。使用Ucinet6数据可视化，Freemans数据集可视化如图1所示。

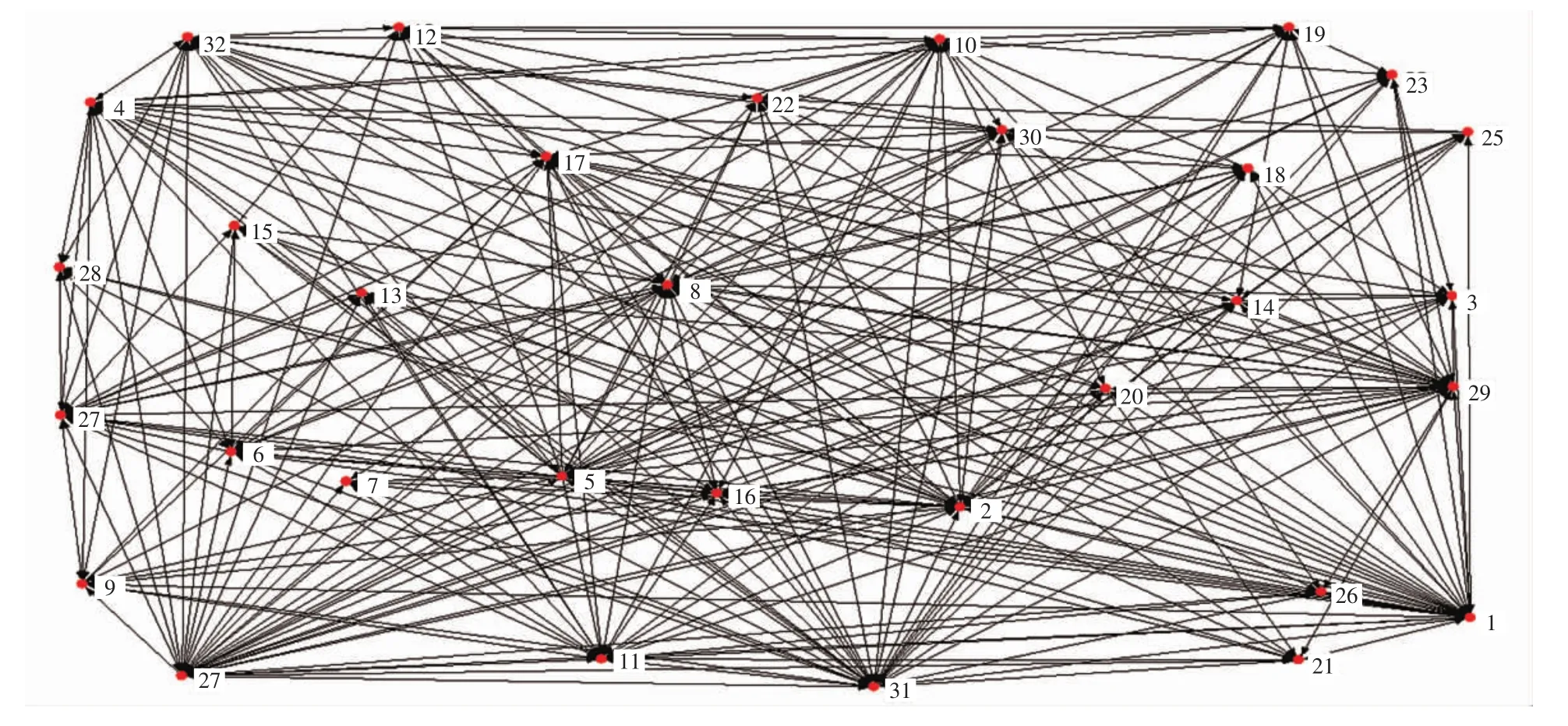
图1 Freemans数据集可视化

使用 PageRank、Pro-PageRank、LeaderRank、DPRank算法指标以及本文提出的JC方法在Freemans数据集进行仿真实验，Freemans_EIES_3网络各中心性算法值如表2所示。

表2 Freemans_EIES_3网络各中心性算法值

由表2可知，识别出的Top 5节点有4个与其他方法一致，各算法识别出的Top 5节点中心性值加粗显示，其中节点24在JC方法中处于Top 5，节点8在其他方法中处于Top 5，SIR传播模型在该数据集仿真实验表明，节点24的扩散能力大于节点8，说明本文提出的JC算法较其他算法更有效。

以算法排序等级为标准，各中心性算法之间的相关性如图2所示。由图2可知，本文算法中节点24、节点5的重要性与其他算法存在较大差异，节点24和节点5在SIR传播模型中，均处在Top 5的位置，说明2个节点处于重要节点位置，本文算法优于其他算法。各中心性算法与SIR模型Kendall tau相似性比较如表3所示。从表3可知，比较了各中心性算法与SIR模型Kendall tau相关性，本文提出的方法比其他方法更接近，证明了提出方法的准确性。

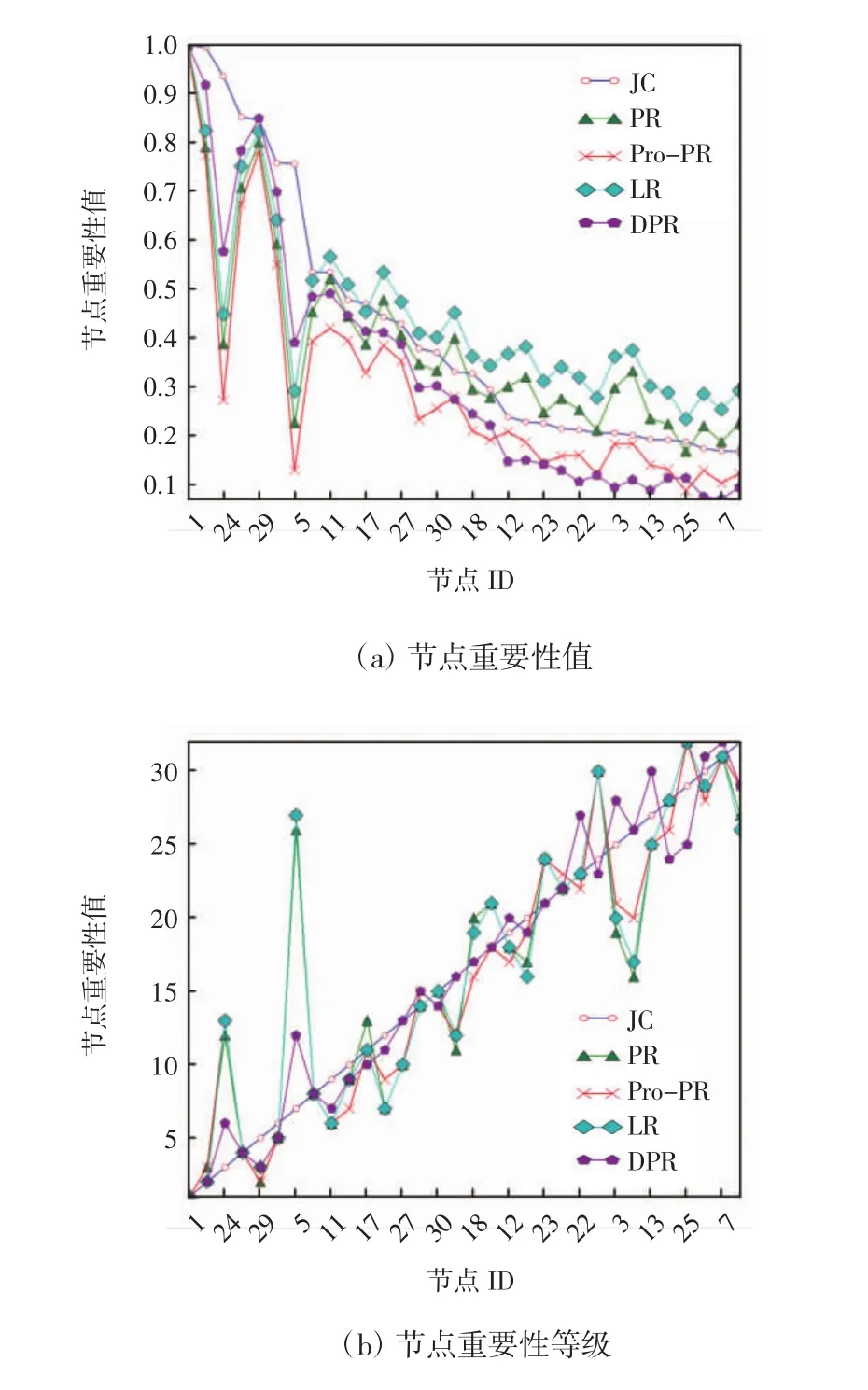
图2 各中心性算法之间的相关性

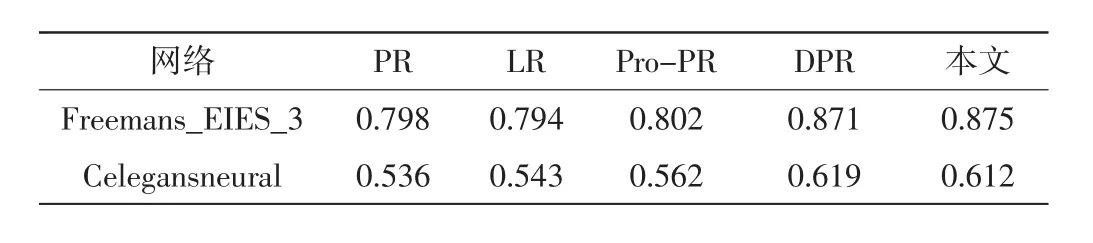
表3 各中心性算法与SIR模型Kendall tau相似性比较

Celegansneural[15]为一个有向含权网络，节点为线虫的神经元，边为神经元突触或间隙连接。网络中包含297个节点和2 359条有向连接，节点平均度15.886，SIR传播模型感染概率β为0.036。

使用 PageRank、Pro-PageRank、LeaderRank、DPRank算法指标以及本文提出的JC方法在Celegansneural数据集进行仿真实验，计算网络中各中心性算法识别出的Top 20节点，网络各中心性算法Top 20节点ID如表4所示。

表4 网络各中心性算法Top20节点ID

由表4可知，本文识别出的Top 3节点中，除DPRank方法外，节点44在PageRank、Pro-PageRank、LeaderRank方法中均处于Top 1；基于SIR传播模型识别出的Top 3节点，其中JC算法Top 3中识别出2个，PageRank、LeaderRank 算法识别出 0 个，Pro-PageRank算法识别出1个，DPRank算法识别出2个；Top 5 节点中，JC 与 PageRank、Pro-PageRank、DPRank算法共同识别出40%，与LeaderRank算法共同识别出80%个节点，证明了本文提出的算法的有效性。通过表3比较各中心性算法与SIR模型Kendall tau相关性，证明本文算法准确性比PageRank、LeaderRank、Pro-PageRank有较大提升，但是略次于DPRank算法。通过在2个数据集进行仿真实验，本文算法在实验效果上与DPRank算法的准确性相似，明显高于其他算法。但在实验过程中，若采用传统迭代计算PageRank及在此基础上改进的其他算法的平稳分布，进而计算节点重要性值的方法，对于数据集Celegansneural节点个数297时间消耗大，本文算法计算效率优于其他算法。采用计算转移概率矩阵转置的最大特征值对应的特征向量方法[16]计算PageRank、Pro-PageRank、LeaderRank、DPRank，算法效率均得到明显提升。

4 结语

本文采用Jaccard指数拓展到有向网络结合叠加随机游走进行关键节点识别，该方法中的Jaccard指数可以是任意的相似度指数的有向版本，将节点相似度和随机游走结合进行关键节点识别，解决了叠加随机游走计算相似和衡量节点重要性方法中有向网络进行扩展的问题。实验结果表明，本文提出的算法可有效地识别出网络中的关键节点且识别精度高。考虑节点间随机游走的倾向性，优于无偏的在节点之间进行随机游走，解决了PageRank算法中存在参数的问题，识别精度明显优于PageRank算法。