弹性边界下静电驱动微梁结构主共振分析

韩建鑫 ，靳 刚 ，李佰洲 ，常云霞

（1.天津职业技术师范大学机械工程学院，天津 300222；2.天津职业技术师范大学天津市高速切削与精密加工重点实验室，天津 300222；3.天津大学机械工程学院，天津 300350）

静电驱动微梁元件具有结构简单、易集成、能耗低、响应频率高等优点，目前已成为微传感器、微制动器、微滤波器、微开关等微机电器件的关键组成部分[1]。值得注意的是，静电力本质上是一种非线性驱动力，可导致微梁产生不稳定的静动态吸合行为[2]。一方面，利用该行为可设计微开关类器件；另一方面，在作动、传感、滤波等微器件设计过程中，这一行为被认为是不稳定的，需要尽量避免。因此，研究静电驱动微梁元件的静动力学行为是微器件力学设计的必要和关键环节[3-6]。微器件设计过程中，梁结构的两端一般或与锚点连接或自由悬置，由于实际加工制造中难免出现误差甚至缺陷，梁与锚点的连接处易产生一定的转角和位移，即呈现弹性边界特性[7-8]。Alkharabsheh等[7]通过数值及实验研究了弹性边界对于静电驱动两端固支浅拱梁动力学特性的影响，指出弹性边界可导致系统出现频率漂移、动态吸合以及振动跳跃等复杂现象。仲作阳[8]理论研究了弹性边界对两端固支微梁和悬臂梁的振型、频率和主共振频率响应的影响。此外，Pallay等[9]通过机构创新与设计，将微悬臂梁的固定端约束弱化为弹性边界，设计了一类基于非线性参激振动的谐振式传感器，该类传感器充分利用柔性支撑模拟梁结构的弹性边界特性，通过一系列静动力学分析与设计，最终通过增大梁的振幅值，有效提升了感测信号的输出强度。因此，考虑将理想边界弱化，引入弹性边界约束，分析弹性边界对于系统静动动力学行为的影响，已逐渐成为微机电系统静、动力学研究的热点问题[10-12]。

弹性边界对于微梁的静动、力学特性具有显著的影响，在微机电器件设计和参数优化时，首先应对其影响机理进行研究。本文以一类微机电系统中常见的单极板静电驱动两端固支微梁结构作为研究对象，综合考虑横向及扭转弹性边界、梁的中性面变形和非线性静电力特点，应用Galerkin方法和多尺度方法研究系统的静动力学行为。理论分析中，将静电力Taylor展开保留至7阶动态项，有效提高了动力学求解精度。本文基于理论结果研究弹性边界弹性刚度对于静态吸合、主共振线性频率以及主共振频率响应及其软硬转换行为的影响。

1 动力学模型

静电驱动微梁结构如图1所示。

图1 静电驱动微梁结构

理想边界条件下静电驱动两端固支微梁结构如图 1（a）所示，其中梁的长宽高分别为 l0、b0、h0，弹性模量为，密度为ρ，梁与极板间的初始距离为g0。考虑制造缺陷或创新设计，将理想固支边界退化为弹性边界，如图1（b）所示，以等效刚度系数为KR的扭转弹簧和等效刚度系数为KT的横向弹簧模拟弹性边界条件[7]。考虑梁的中性面变形及静电力作用，可建立静电激励作用下微梁的横向振动方程[13]为

上述方程对应的边界条件为

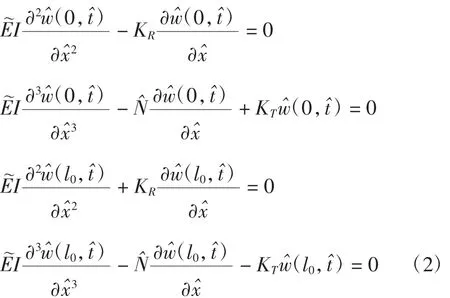
为了便于分析，引入如下无量纲量

与方程相对应的无量纲边界条件为

其中，方程（4）和（5）中的无量纲参数为

微梁的变形包括2部分，直流电压导致的静态变形和交流电压导致的动态变形，即无量纲横向变形w（x，t）可表示为

式中：ws（x）为无量纲静态变形；wd（x，t）为无量纲动态变形。

若不考虑交流电压激励的影响，则结合方程（4）和（7）可直接推导得到微梁的静态方程

该静态方程可通过Galerkin方法进行计算与分析。

结合Galerkin方法，系统的动态变形部分可近似表示为

式中：φj（x）为微梁的j阶振型函数[12]；δj（t）为j阶振动的广义坐标，即j阶振动函数；M为最高振动阶次。

研究梁的主共振动态响应时，可近似认为M=1。将方程（7）代入到方程（4），将静电力部分泰勒展开至wd（x，t）的7次方，并根据直流电压幅值远大于交流电压幅值这一特性，忽略交流电压的平方项[14]，简记u（t）=δ1（t），φ（x）=φ1（x）。应用Galerkin方法，可得到微梁的主共振动力学方程

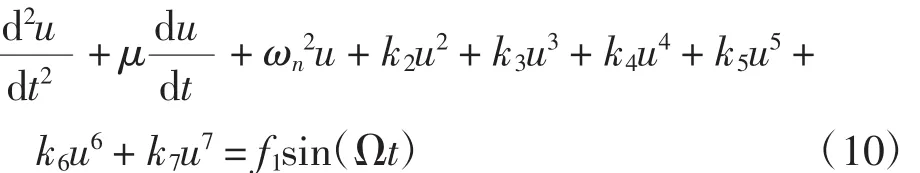
式中：ωn为系统的无量纲一阶线性频率。

相关参数表达式为

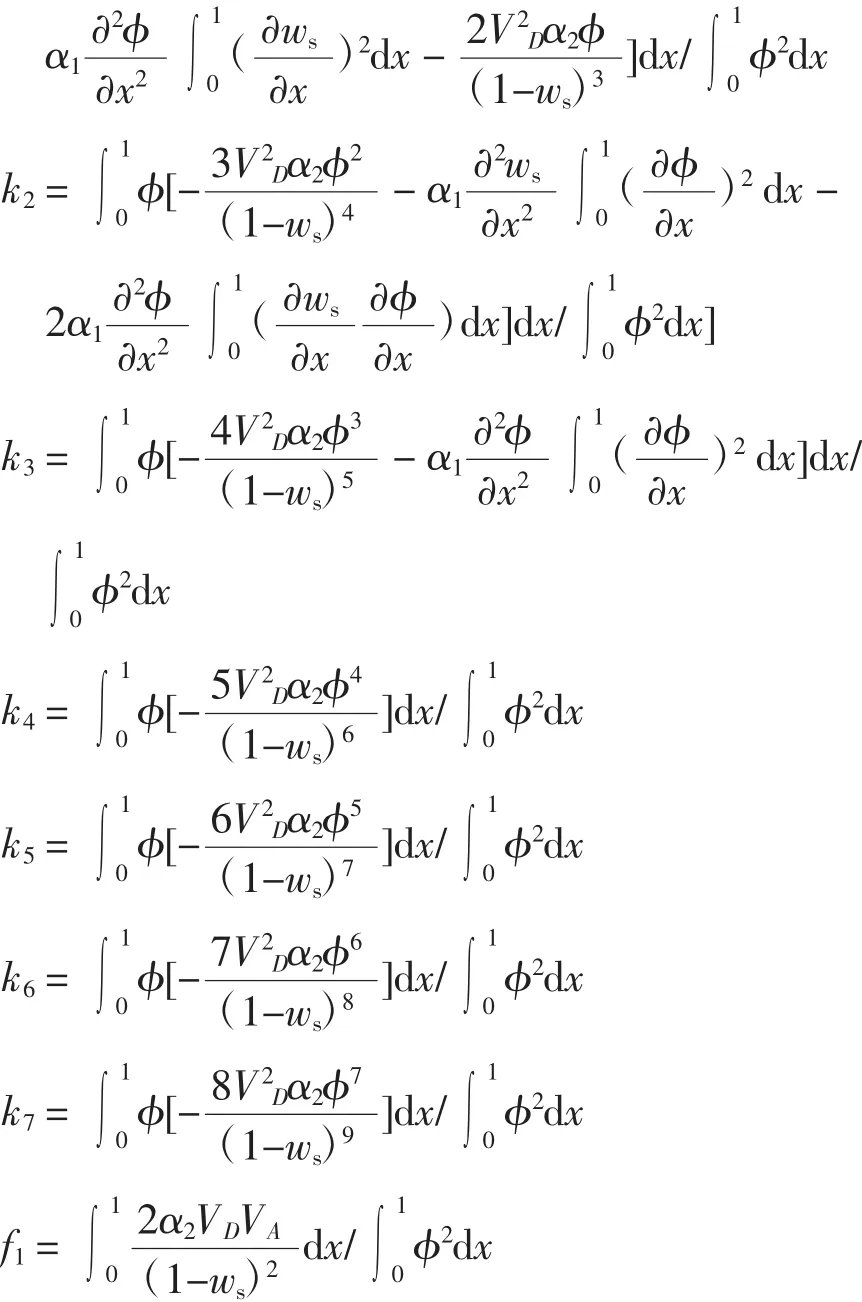
2 主共振近似解

应用多尺度方法[15]对方程（10）进行主共振分析。引入代表对应项为小量的无量纲标志ε，可得动力学方程如下

假设系统的解可表示为如下形式

式中：Tn= εnt，n=0，1，…，6。

式中：γ=σT6-β；a为振动幅值；β为振动相位。

相关参数表达式为

将方程的稳态解代入方程即可得动态响应。

3 动力学分析

3.1 收敛性分析

为验证本文程序及理论解的正确性，采用文献[16]的物理参数，计算理想边界情况下系统的静动态特性。静态位移解通过五阶Galerkin离散计算而得到，其中静电力部分直接利用牛顿辛普森积分公式计算，可避免静态位移不收敛情况[17]，静态最大位移由ws,max=max（ws）计算，响应最大位移由 wmax=max[ws+u（t）φ（x）]计算。具体仿真参数为[16]：E～=166 GPa，ρ=2 332 kg/m3，l0=510 μm，b0=100 μm，h0=1.5 μm，g0=1.18 μm，ε0=8.854 × 10-12，N=8.7，μ =0.239，最终推导所得理论模型的收敛性分析如图2所示，其中解的稳定性根据非线性振动理论中Jacobi矩阵的特征值进行判断。通过与文献[16]的数值计算结果对比可知，本文程序正确且理论解具有较高的计算精度。

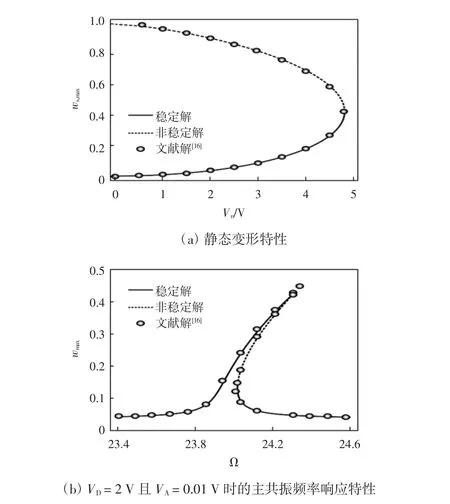
图2 推导所得理论模型的收敛性分析

3.2 位移与频率分析

文献[7]中的扭转刚度和横向刚度系数，令KT=40 N/m，KR=10-7N·m/rad，最终得到系统的最大静态位移与一阶线性频率ωn随直流电压的变化情况如图3所示。从图3中可以看出，弹性边界条件下，系统直流偏置电压行程降低，吸合电压减小；吸合前相同直流电压作用下，弹性边界会导致微梁的最大静态位移偏大，一阶线性频率偏小。若设计人员需要对微梁的谐振频率进行设计，则弹性边界会导致最终设计结果比理论计算结果小。实际上，弹性边界对静电微开关设计具有积极的促进作用，可有效减小吸合电压进而降低器件开关过程中的能耗。而对于动态结构来讲，弹性边界使得器件静态变形增大，共振频率向小方向漂移，最终导致设计响应与实际响应出现偏差。因此，无论从哪方面考虑，研究弹性边界作用下系统的静动力学都是必要的。

图3 系统的最大静态位移与一阶线性频率随直流电压的变化情况

3.3 主共振响应分析

理想边界和弹性边界情况下系统的主共振频响曲线如图4所示，其中相关参数取值为[16]：VD=2V，VA=0.01 V。从图4中可以看出，弹性边界的存在可有效增大系统的最大振动响应幅值，同时减小系统的一阶共振频率，此外可导致系统出现软硬转换行为。进一步研究探讨了弹性边界刚度系数对于系统频率响应的影响，结果如图5所示。从图5（a）中可以看出，横向刚度KT的增大使得频响曲线向右偏移，且曲线的硬弹簧特性更加明显；最大振动位移略有减小，软硬转换现象减弱。从图5（b）中可以看出，扭转刚度KR的增大同样会使得频响曲线向右偏移，但曲线的硬弹簧特性及最大振动位移不会发生明显改变。

图4 理想边界和弹性边界情况下系统的主共振频响曲线

图5 弹性边界对系统主共振频响曲线的影响

4 结语

本文研究了弹性边界对于系统的主共振行为的影响。通过应用Galerkin方法和多尺度方法，推导获得了考虑7次非线性动态响应的微梁结构主共振近似理论解。该理论解具有较高计算精度，能够用于研究不同边界条件及物理参数对于系统静动力学行为的影响。从静态位移、一阶线性频率和主共振频率响应3个方面探讨了弹性边界的影响作用，发现弹性边界会导致静态吸合电压减小，静态变形增大，一阶线性频率整体降低，频响曲线最大振幅增大，复杂度增大，易诱发频响曲线软硬转换行为。因此，本文研究对于考虑弹性边界的静电驱动微梁结构分析与设计具有一定的理论指导作用。