基于多项Logit 模型的高速铁路客流分配实证研究

程 谦，卢万胜，曲思源，单仕平

（1.南京铁道职业技术学院 运输管理学院，江苏 南京 210031；2.中国铁路上海局集团有限公司运输部，上海 200071；3.中国铁路上海局集团有限公司 客运部，上海 200071)

0 引言

我国高速铁路的快速发展，极大地方便了旅客出行。旅客在选择高速铁路出行时，由于个体出行需求与列车服务水平存在差异，对不同列车表现出不同的选择行为。深入研究旅客对不同高速铁路列车产品的选择行为、定量分析不同列车间的客流分配规律，可以为编制更加契合旅客需求的列车开行方案提供技术支持，也可以帮助高速铁路运输企业提升服务水平，有效提高列车上座率。

中外学者应用不同方法对客流分配问题进行深入研究。聂磊等[1]根据铁路旅客出行链构建客流分配网络，建立铁路客流分配的UE 模型，设计改进F-W 算法；佟璐等[2]以旅客出行效益最大化为目标构建铁路客流分配的UE 模型，设计混合算法，应用京沪高速铁路列车开行数据验证模型和算法的有效性；豆飞等[3]引入熵增加原理构建UE 配流模型，应用改进F-W 算法对简单算例进行求解，验证模型的有效性。由于选择行为是影响网络客、货流分配的主要因素之一，也有学者应用离散选择模型研究网络客、货流分配问题。Agostino 等[4]应用巢式选择行为模型研究铁路列车服务水平与价格政策；王文宪等[5]应用巢式选择行为模型分析铁路旅客面对普速铁路不同客运产品的选择行为；王文宪等[6]应用多项Logit模型(MNL)分析高速铁路旅客在面对G 类高速列车和 D 类高速列车时的选择行为；李亚[7]应用巢式选择行为模型研究铁路旅客对出行时段与乘车方式的联合选择行为；白杰[8]应用巢式选择行为模型分析计算不同运输方式下货运产品市场分担率。

上述研究多数是将不同类别列车产品作为出行旅客选择集，但未涉及出行旅客对具体列车选择行为研究。在给定时间范围内，同一类列车中有多趟列车在线运营，以某一具体列车为研究对象分析旅客选择行为并预测上座率更具有现实意义。在既有研究基础上，以列车作为旅客出行选项，应用MNL 模型构建高速铁路客流分配模型，根据路网真实运营数据，标定模型参数，分析影响旅客选择的不同列车服务属性因素，最后应用历史客流数据验证客流分配的准确性。

1 基于MNL 的高速铁路客流分配模型

高速铁路列车开行方案确定了列车开行径路、列车始发终到车站及列车停站方案。不同城市OD间的高速铁路列车服务网络是基于列车开行方案构成的不同列车的集合。一些列车站停次数少，旅行时间短；一些列车站停次数多，旅行时间长。因此，旅客面对不同列车表现出不同的选择行为。

（1）根据Kenneth[9]的理论，假设旅客n面对的列车选择集合为C，则旅客选择第i次列车出行的效用函数Uni计算公式为

式中：Uni为旅客n选择i次列车的效用；Vni为旅客n选择i次列车可以被观测到的效用；εni为旅客n选择i次列车效用的误差项，假设误差项独立且服从Gumbel 分布。

（2）通常假设Vni是包含列车i的服务水平变量和旅客n的个体特征变量xnik的线性函数，计算公式为

式中：βk为待估参数；xnik为影响旅客n选择i次列车的第k个属性。

（3）根据效用最大化原则，旅客n选择列车i的概率可以表示为

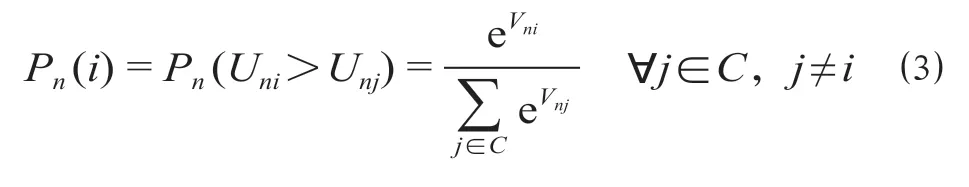
式中：Pn(i)为旅客n选择列车i的概率；e 为常数。

（4）高速铁路列车服务网络中，一日内同一城市OD 间有多趟列车运行，在考虑OD 全体出行旅客列车选择行为的前提下，旅客个体特征可以视为常量，列车服务水平变量是影响一个OD 对某一列车被选择概率的关键因素，设Vi是i列车可以被观测到的系统效用，计算公式为

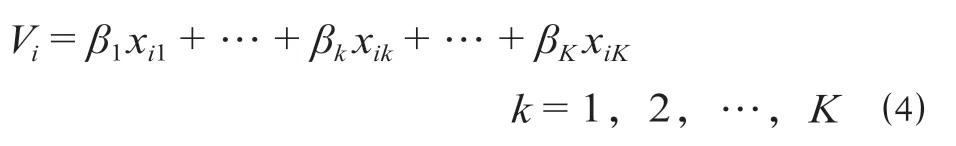
式中：xik为OD 对列车i的服务水平变量，包括列车出发时间、到达时间、票价、站停次数、旅行时间等，为方便叙述，令xi,stop表示i列车经过中间车站的停站次数，xi,time表示i列车在一日内的不同开行时段，xi,price表示i列车票价；βk为待估参数，可应用极大似然估计法求解上述参数。

（5）公式 ⑷ 仅包括列车i的服务水平变量，不包括旅客的个体特征变量。在已知OD 对总客流的前提下，可以应用列车被选择的概率确定列车的旅客发送人数，计算公式为

式中：P(i)为列车i被选择的概率为OD 对中除列车i的其他列车系统效用Vj之和。

（6）根据某一列车的服务属性，应用公式 ⑸，可以得出列车选择概率。设OD 对的旅客发送总量为NOD，则该OD 对某一列车的客流分配结果的计算公式为

式中：PredOD(i)为OD 对列车i的客流分配结果。

（7）在得出客流分配结果后，可以应用历史客流数据与客流分配结果比较，验证模型预测的准确率。设OD 对历史同期某次列车旅客发送人数为，OD 对旅客发送总人数为，则应用历史客流数据计算列车客流分配比例P'(i)的计算公式为

基于历史客流数据预测OD 对某一列车客流分配结果的计算公式为

式中：(i)为基于历史客流数据预测OD 对列车i的客流分配结果。

（8）应用客流统计数据标定客流分配模型待估参数时，可以根据模型初始对数似然函数值lnL(0)、模型似然函数最优值lnL(β)、麦克法登系数指标评价模型拟合优度。lnL(0)为客流分配模型全部变量取初始值0 时的对数似然函数值；lnL(β)为客流分配模型全部变量满足最优条件时的对数似然函数值。既有研究表明[9]，当lnL(β)显著大于lnL(0)，麦克法登系数大于0.2 时，可以判定客流分配模型有效收敛。

2 实证研究

为分析旅客对不同高速铁路列车产品的选择行为、预测不同列车客流分配结果，收集2017 年6月一周内华东地区高速铁路路网南京—上海、安庆—上海、安庆—南京南、池州—苏州、芜湖—无锡5 个城市OD 的日均二等坐席的客流统计数据，共645 38 条旅客乘车信息，样本量能够支撑客流分配模型构建。应用样本数据标定客流分配模型参数，以南京—上海区段为例，预测不同列车客流分配结果，验证模型预测能力。

2.1 客流分析

城市OD 间的全日开行列车总数构成了旅客出行选择集C，由于城市经济发展水平的差异，不同城市OD 日均开行列车数量、旅客发送人数及列车平均发送人数不同，数据集中5 个城市OD 日均开行列车数统计如表1 所示。

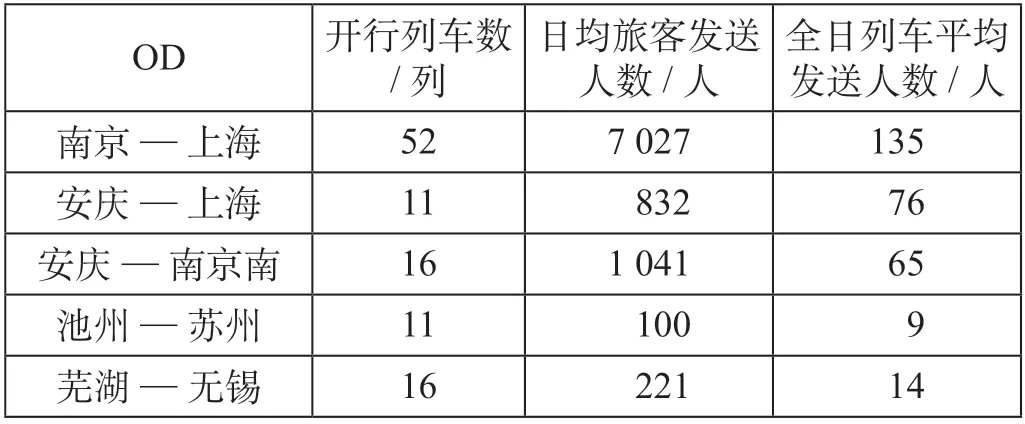
表1 5 个城市OD 日均开行列车数统计Tab.1 Daily average number of trains operated in 5 OD pairs

根据列车站停次数、列车出发时间范围以及票价的差异，可以将不同城市OD 间开行列车划分为不同的列车服务产品。在所选数据集中，以南京—上海为例，南京—上海站停次数不同列车旅客发送人数如表2 所示，南京—上海不同时段列车旅客发送人数如表3 所示，南京—上海不同票价列车旅客发送人数如表4 所示。

从表2 可以看出，站停次数少的列车旅客发送人数大，3 站停列车是沪宁高速铁路(南京—上海)旅行时间最短的列车产品，旅客发送人数最多，全日列车平均发送人数达到342 人。表3 描述了一日内不同时段开行列车发送人数的分布规律，可以 看 出8 : 00—11 : 00，14 : 00—16 : 00，17 : 00—18 : 00，20 : 00—21 : 00 时段是南京—上海的高峰时段。表4 反映了不同票价类别列车产品发送人数的差异，目前高铁列车产品主要包括G类(300 km/h)与D 类(250 km/h 或200 km/h)列车，统计数据表明D类列车全日列车平均发送人数略多于G类列车。

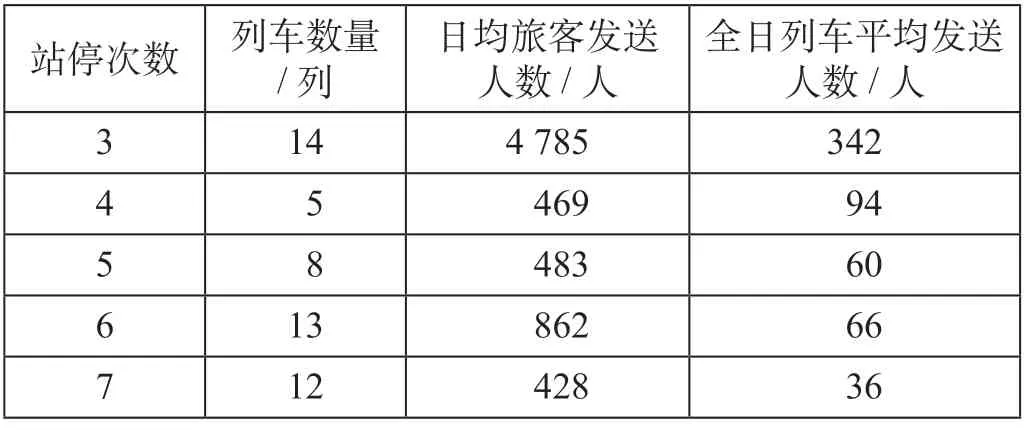
表2 南京—上海站停次数不同列车旅客发送人数Tab.2 Passenger volume between Nanjing and Shanghai withdifferent stops

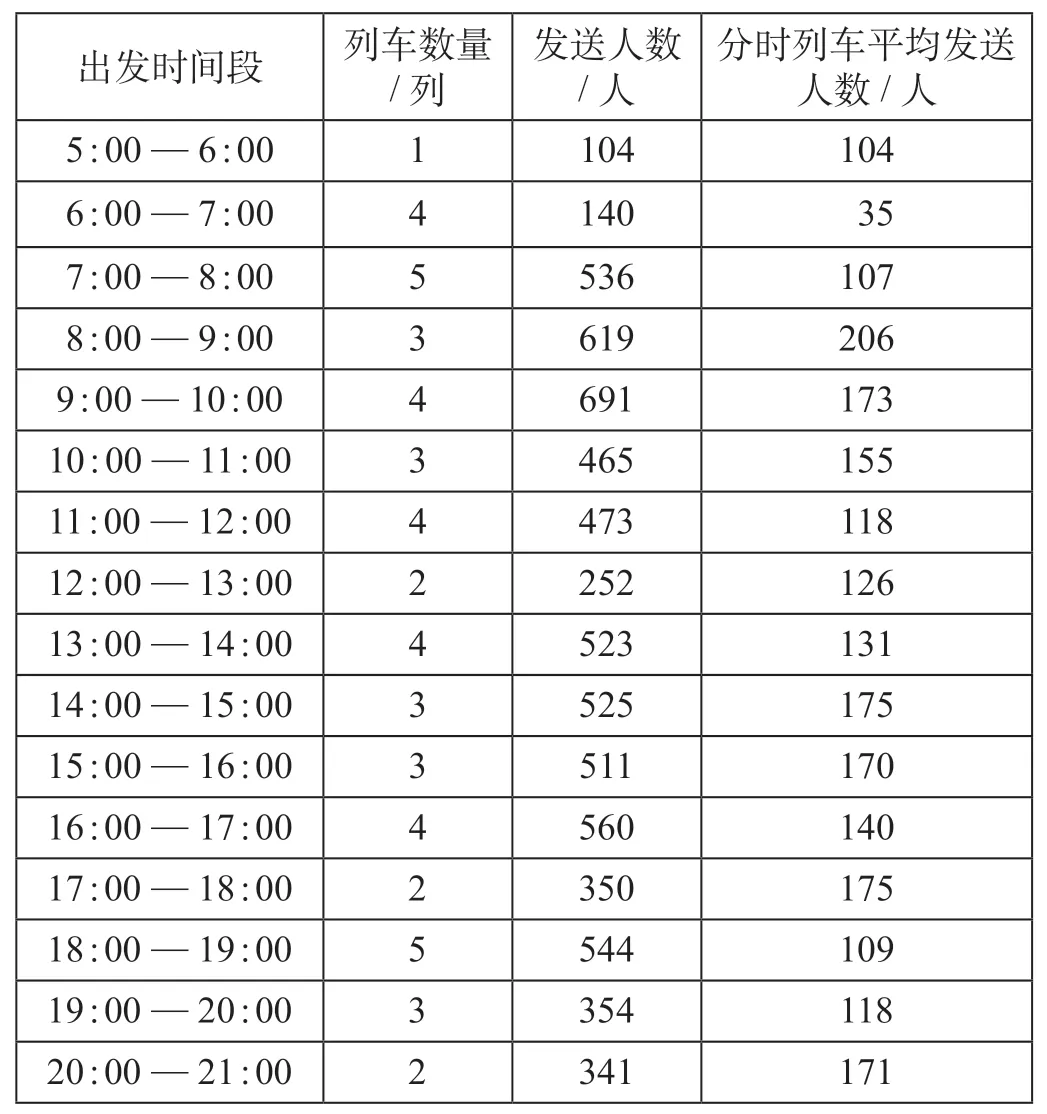
表3 南京—上海不同时段列车旅客发送人数Tab.3 Passenger volume between Nanjing and Shanghai at differenttime periods

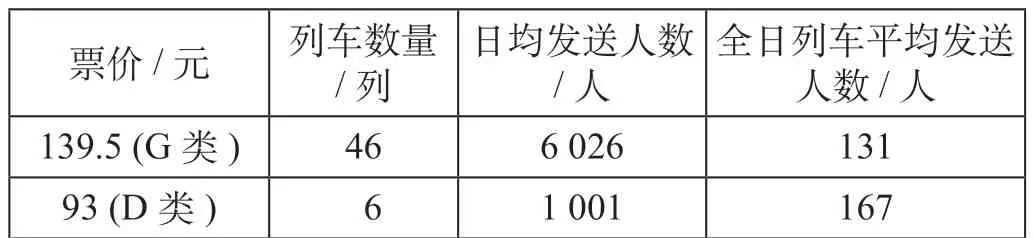
表4 南京—上海不同票价列车旅客发送人数Tab.4 Passenger volume between Nanjing and Shanghai withdifferent ticket prices

2.2 变量赋值

影响旅客选择的列车服务属性解释变量包括列车出发时间、到达时间、票价、站停次数、旅行时间等。列车站停次数越多，则旅行时间延长，站停次数与旅行时间高度相关。相比到达时间，城际出行旅客对出发时间更为敏感。因此，研究选择列车出发时间、票价及站停次数作为模型解释变量。变量赋值如表5 所示。xi,price变量取值为南京—上海开行了D 类与G 类列车二等座席客票价格。

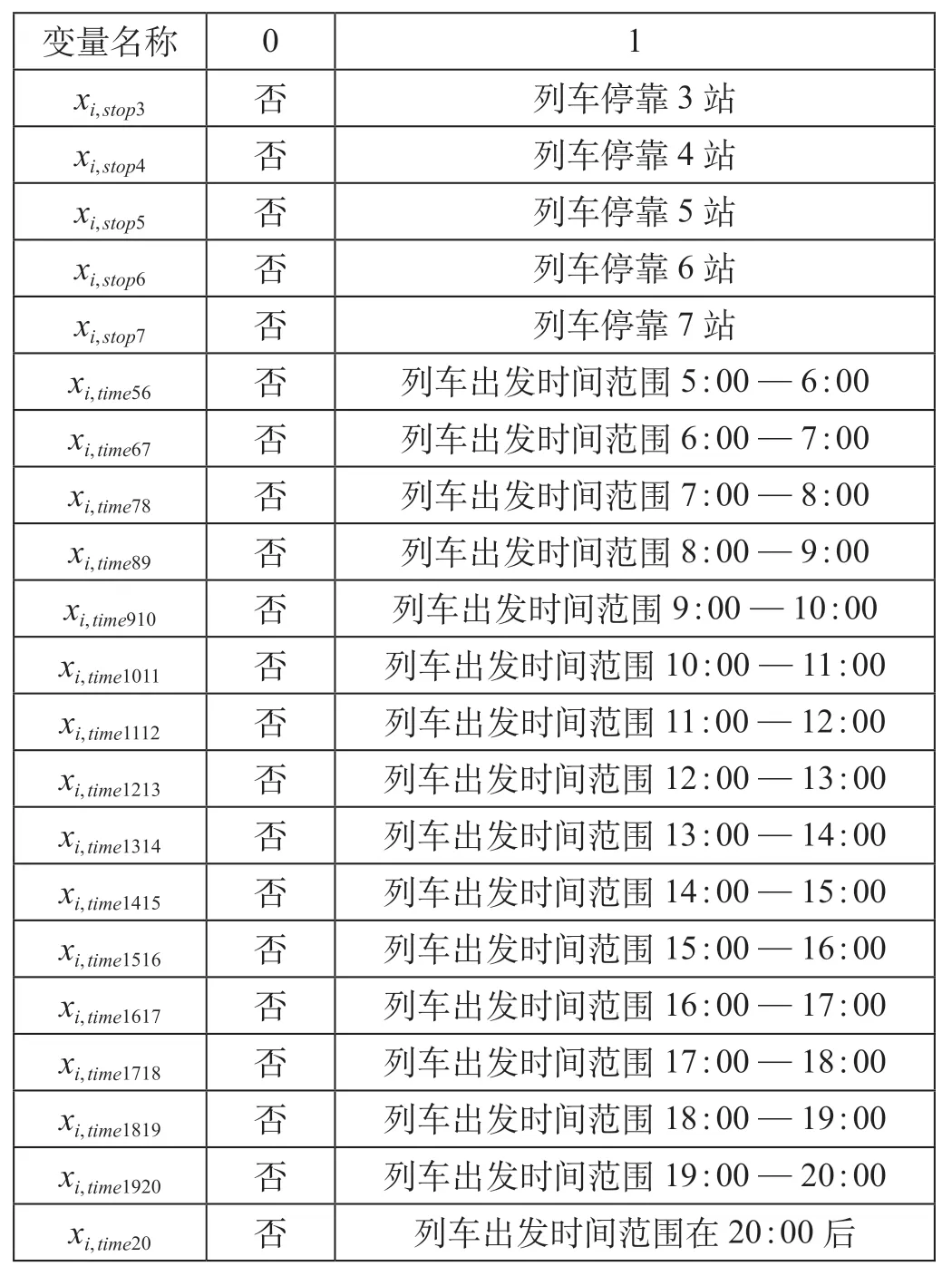
表5 变量赋值Tab.5 Variables assignment

2.3 参数估计

解释变量的参数值表明了在同一列车选择集中，不同解释变量对列车选择重要性的影响，应用参数标定结果可以计算不同OD 对不同列车的客流分配比率。解释变量的参数估计如表6 所示。

模型的拟合指标反映了应用所选数据集标定客流分配模型的拟合效果，模型拟合指标如表7 所示。由表7 可知，模型lnL(β)指标收敛明显，麦克法登系数均超过0.2，表明模型的拟合效果较好。

从参数估计结果可以看出，在不同城市OD中，不同列车出发时间段对不同列车的选择影响程度表现出不同的差异性。出发时间段在凌晨(5 : 00—6 : 00)和夜晚(20 : 00 后)的参数估计为负值，说明在同等条件下，出行旅客很少选择这2 个时间段出行。估计结果也表现了不同城市旅客出行时间选择的差异性，南京—上海与安庆—南京南2 个OD间6 : 00—8 : 00 时间范围内，参数估计值高于其他城市OD，说明在其他变量保持不变的情况下，2 个OD 间的出行者更愿意选择早班高速铁路出行，体现了这2 个OD 客流的通勤特征。此外，南京—上海19 : 00 后时间范围内的参数估计值高于其他城市OD，说明南京—上海旅客选择晚班高铁出行的意愿强于其他城市旅客。

通常情况，列车票价越高，选择列车人数越少。研究表明，仅有南京—上海存在G 类与D 类2 类高速铁路列车的价格差异，参数估计结果均为负值，符合研究预期判断。

在表6 中，5 个城市OD 对列车站停次数的参数估计结果均为负值，并且随着站停次数的增加，旅客选择列车的负效用增大，说明由于列车停站增加了出行时间，旅客对列车的选择与列车站停次数呈负相关关系的特征。对比列车出发时间、票价以及站停次数等不同解释变量的参数值，可以看出站停次数对旅客乘车选择的影响大于列车出发时间与票价的影响。

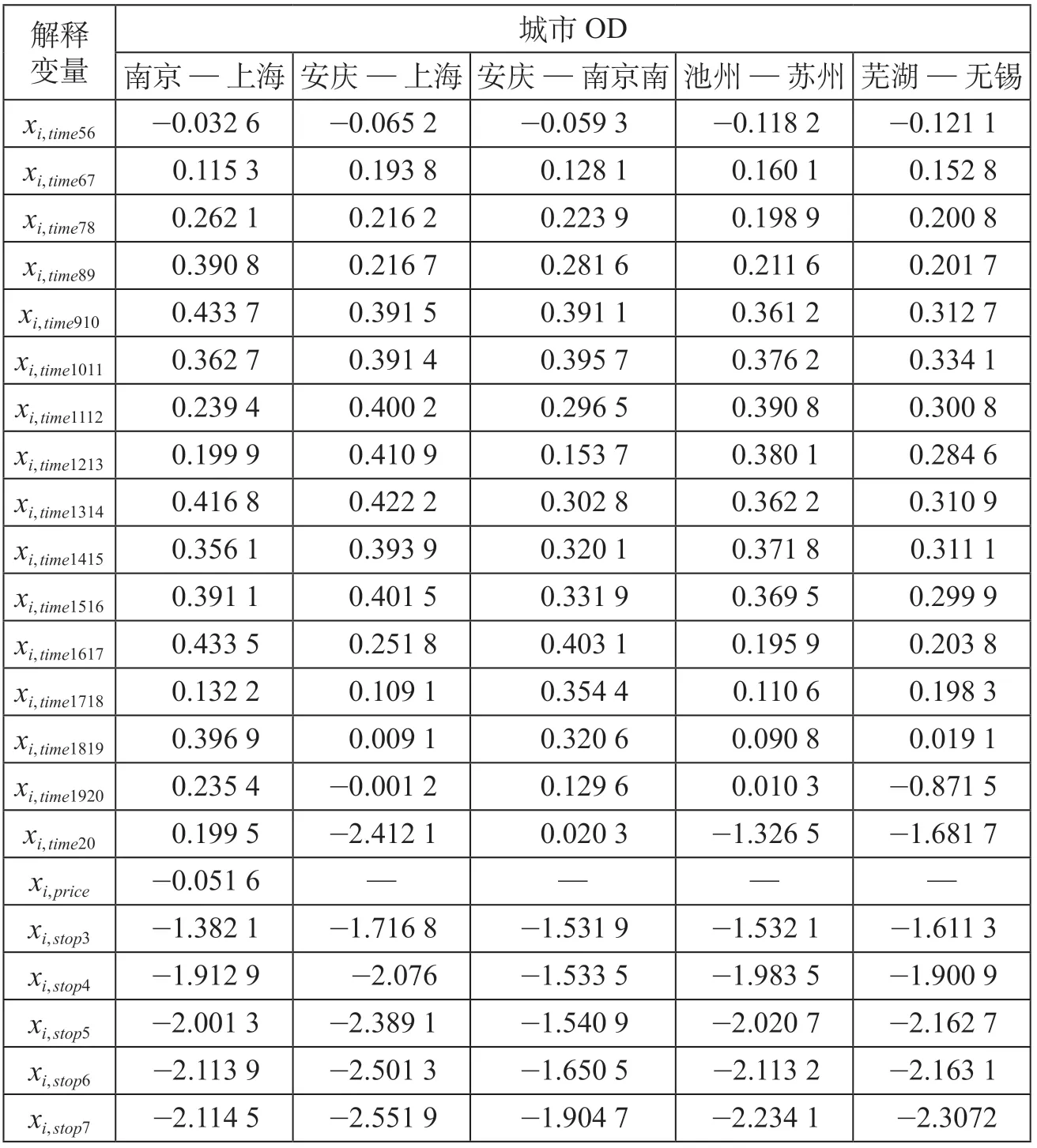
表6 解释变量的参数估计Tab.6 Calibration result of the model

表7 模型拟合指标Tab.7 Fit index of the model

2.4 客流分配

选取2017 年7 月第1 周南京—上海旅客发送量数据，应用多项Logit模型(MNL)与历史数据分别预测了南京—上海各次列车旅客发送量的日均值，并与当日各次列车的实际乘车人数进行对比。

分析应用多项Logit 模型与历史数据预测2 种方法分配的1 周内日均上车人数与实际上车人数累计误差的平均水平，用以验证模型预测的有效性。模型预测精度比较如图1 所示。

从图1 可以看出，多项Logit 模型预测各次列车旅客发送人数的误差值均低于对应的历史数据预测结果，多项Logit 模型的预测结果更为平稳，前者的预测精度优于后者。

图1 模型预测精度比较Fig.1 Comparison of forecasting accuracy

通过应用模型计算得到2017年7月5日南京—上海各次列车的客流分配结果，与实际发送人数进行对比，客流预测比较如表8 所示。通过计算结果可以看出，MNL 客流分配模型分配结果与实际旅客发送人数的预测偏差值在±5%的范围内，该模型可以较好地预测客流。

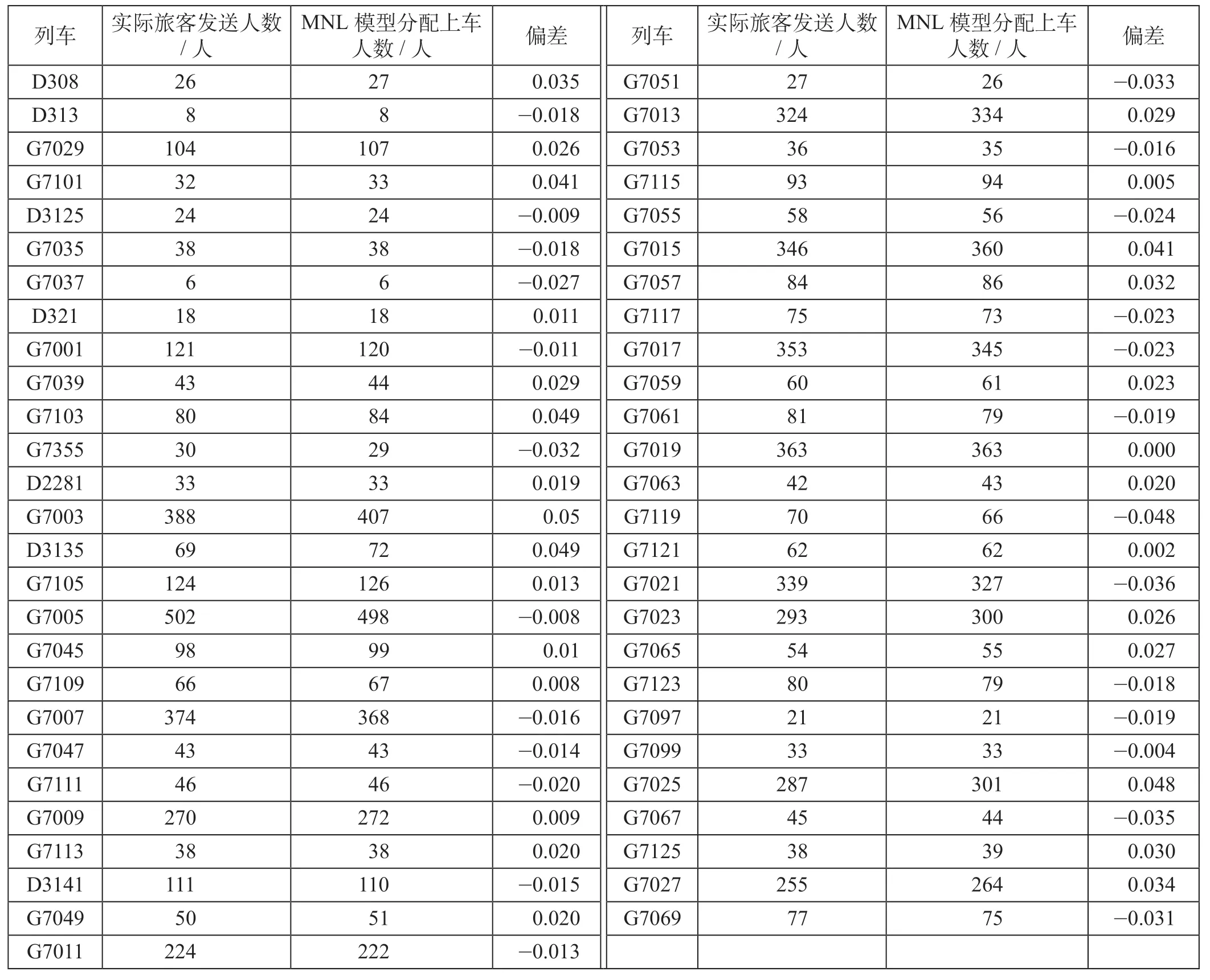
表8 客流预测比较Tab.8 Comparison of passenger flow forecasting

3 研究结论

（1）通过引入列车出发时间、车票价格与站停次数作为出行旅客列车选择行为的影响因素变量，应用多项Logit 模型(MNL)构建高速铁路同OD 不同列车的客流分配模型，预测不同列车客流分担率，结果与实际统计值偏差在5%以内，说明模型具有较好的预测能力。

（2）准确预测不同列车客流需求，有利于不同列车相互竞争关系在中短期铁路运输组织决策分析，还应进一步考虑中转换乘、动车组类型等相关因素及个体特征对旅客乘车选择行为的影响，进而提高客流分配预测精度，为铁路运输企业提供契合运输市场需求的研究依据。