支持向量回归的机器学习方法在海浪预测中的应用

王燕，钟建，张志远

（中国人民解放军91001部队，北京100161）

1 引言

海浪周期、波向、有效波高等海况特征是海洋工程建设、海上运输、环境保护和军事行动等活动必须考虑的重要安全因素[1]。其中，海浪有效波高最为重要，其预测的时效和准确性依然是目前亟需解决的关键问题。为提高海浪预测的准确性，国内外学者开展了不同的预测方法研究，主要有经验模型、数值模拟[2]和机器学习法等。基于经验模型，通过先验模型假设进行海浪预测，例如自回归移动平均方法（Auto-Regression and Moving Average Model，ARMA），但预测能力有限。基于数值模型，例如海浪模型（WAve Model，WAM）[3]、近岸海浪数值模型（Sim-ulated WAves Nearshore，SWAN）[4]、第三代海浪模型（WAVEWATCH III）[5]和海浪数值模式（MArine Science and NUmerical Modeling，WASNUM）[6]等，通过求解海浪谱控制方程来模拟和预测海浪要素，该方法对于广阔海域海浪具有显著的预测能力，但对于复杂地形的近岸海域，其预测能力欠佳。

由于机器学习方法不受高性能计算和大样本数据集输入的限制，近年来，人工神经网络[2,7-12]、模糊推理系统[2,13-14]和遗传规划[15-17]等机器学习方法被广泛应用于海浪要素预测，有效弥补了其他两种海浪预测方法的不足。支持向量机（Support Vector Machine，SVM）[18]作为一种新颖的机器学习方法，已广泛用于海上活动和沿海工程大气海洋环境要素的预测。Mohandes等[19]利用SVM方法进行风速预测。Asefa等[20]利用SVM方法实现了对复杂海况的海流预测。Salcedo-Sanz等[21]利用SVM方法开展了风电场风力涡轮机中的风速预测。Raghavendra等[22]详细阐述了SVM方法在水文领域的应用情况，并指出其对大气海洋环境的预测能力已得到社会广泛认可。2009年，Mahjoobi等[1]利用支持向量回归（Support Vector Regression，SVR）方法建立了海浪有效波高预测模型，将风速作为输入信息，并指出SVR方法对有效波高的预测技巧优于人工神经网络模型、多层感知机模型和径向基函数模型，且所需计算时间相对较少。

海浪通常可分为风浪和涌浪。风浪是受局地风影响的海浪，当海浪传播到远离其产生区域时，或当它们的传播相速度超过局地风速时，则为涌浪[23]。由于涌浪的存在，如果在SVR预测模型中仅考虑风速作为输入信息，则无法达到最佳预测效果。针对这个问题，本文考虑历史海浪状态的影响，设计了多组风浪信息组合方案，利用SVR方法建立了渤海海域有效波高预测模型，并开展不同风浪信息组合对有效波高预测的敏感性试验，分析对比不同输入信息对有效波高预测技巧的影响。

2 预测区域和实验数据

渤海属于我国内陆海，海岸线崎岖，岛屿众多，地形、地貌复杂，对该海域近岸海浪的准确预测存在较大难度。随着我国经济的快速发展和军事实力的增强，对渤海海域海浪的预测需求日益迫切。本文选取渤海海域为预测区域（见图1），研究采用的观测数据为近岸浮标数据（121°40′48″E、38°9′31″N），观测要素为海浪有效波高和10 m风速，时间分辨率为1 h，时间区间为2012年11月15日—2013年2月15日。本文将观测数据集分为两组，第一组（810个样本）用于预测模型训练，第二组（480个样本）用于预测结果验证。

图1 预测区域和浮标位置（见黑色小框）

渤海湾属于半封闭海，太平洋涌浪很难影响到渤海湾海域，因此该海域主要为风浪。Pierson等指出风速U和有效波高遵循如下经验关系[24]，

式中：g是重力加速度，U是10 m风速。基于该风浪经验关系公式，得到风浪状态和涌浪状态之间拟合曲线（见图2），曲线下方（上方）的值表示风浪（涌浪）为主的海浪状态。统计发现涌浪为主的海浪状态所占比例约为30%，表明该海域涌浪存在且不能忽视。

图2 海面风速和有效波高的散点分布图

3 建模方法和参数优化

SVM是在统计学习理论基础上发展起来的基于结构风险最小化原则的机器学习理论[18]，其具有较高的泛化推广能力。通过将低维的样本空间映射到高维空间来实现低维非线性问题向高维线性问题的转化，能够较好地处理小样本、高维度、非线性等问题。研究发现，SVM方法在数据分类和数据回归方面具有显著优势，且其预测技巧优于人工神经网络模型和模糊推理模型[20]。

SVR方法是通过SVM方法进行回归分析的一种机器学习方法。为简化SVR模型复杂度并提升预测技巧，SVR模型通过构造核函数解决上述问题。核函数的选择能够很好地解决维数问题，并克服机器学习方法中存在的收敛速度慢、局部极值、过学习与欠学习等问题。常用的核函数有：线性函数、S函数、多项式函数和径向基函数等。本文通过敏感性数值试验评估后，选择径向基核函数，与其它核函数相比，径向基核函数所需输入参数少，数值计算限制少。具体表示为：

式中：x∈Rn，xi是输入要素向量，γ是径向基核函数参数。

径向基核函数的参数γ和SVM模型中的惩罚参数C的选择会极大的影响模型的预测结果，应根据不同的应用领域来取值。为了优化参数γ和C，本文使用粒子群优化（particle swarm optimization，PSO）算法选择最佳匹配参数。PSO方法最初由Kennedy等提出[25]，与遗传算法相比，PSO没有复杂的继承、变异、选择和交叉的操作，实施更为简单，通过交叉验证进一步确定PSO算法在本文可用。

4 模型建立和性能评估指标

本文基于SVR机器学习方法，建立了渤海海域有效波高短期预测模型，并利用浮标观测数据进行3 h、6 h、12 h和24 h有效波高预测试验和结果验证。前人研究成果表明，与风向、风作用时间和风区长度等输入信息相比，风速对海浪预测技巧的提升更为重要[2]。此外，由于历史海浪状态能够改变海面粗糙度分布，因此本文在考虑风速影响的情况下，同时考虑海浪状态的影响，在预测模型中引入历史海浪状态作为输入信息。为分析不同的风浪输入信息组合对有效波高预测能力的影响，本文开展了多组有效波高预测的敏感性试验，共设计了32组数值试验（见表1），分别以M1—M32命名，表中符号H和U分别表示有效波高和10 m风速，下标表示时间，例如U0表示前当风速，U-3表示预测前3 h风速，U3表示未来3 h风速，H0表示当前有效波高，H3表示未来3 h有效波高。

表1 不同输入信息组合的数值试验

为定量评估SVR模型的预测能力，本文选择均方根误差（Root Mean Square Error，RMSE），相关系数（R）和一致性指数（Index of Agreement，IA）作为评估指标，其定义如下：

式中：xi(yi)是观测（预测）值，n表示样本总数。xˉ(yˉ)表示观测（预测）值的平均值。

5 输入信息敏感性试验和结果分析

5.1 仅输入10 m风速信息的预测试验

基于SVR模型，将当前风速U0作为输入信息，设计了5组数值试验（M1、M2、M3、M4、M5）来评估当前风速U0对有效波高的预测技巧。预测结果误差统计表明（见表2），在只考虑当前风速U0情况下，仅对未来6 h以内的有效波高具有较高的预测能力，尤其对未来3 h的有效波高预测技巧达到最高，其RMSE、R、IA分别为0.277、0.913和0.935，但对6 h以上的有效波高没有显著的预测能力。

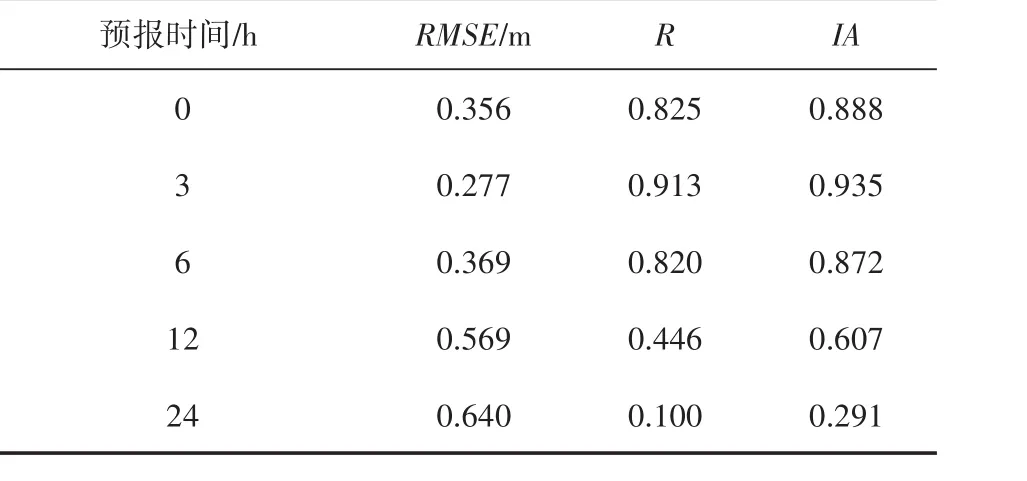
表2 仅输入10 m风速信息的预测试验的有效波高预测误差

5.2 仅输入当前海浪信息的预测试验

由于历史海浪状态能够影响海面粗糙度，本文设计了4组（M6、M7、M8、M9）数值试验，将当前有效波高H0作为SVR模型的输入信息，评估其对有效波高的预测技巧。从不同预测时刻的有效波高误差统计结果可见（见表3），未来3 h有效波高预测的RMSE、R、IA分别为0.291、0.886、0.937，其具备一定预测技巧，但随着预测时效的延长，误差越来越大，12 h后完全失去预测能力。此外，比较表2和表3的误差结果，作为输入信息，当前风速U0对有效波高预测的贡献要高于当前有效波高H0，但当前有效波高H0的作用不可忽视，因此基于SVR模型的有效波高预测应当考虑当前有效波高H0的影响。

表3 仅输入当前海浪信息的预测试验的有效波高预测误差

5.3 不同风浪信息组合的预测试验

基于上述试验结果，本文将当前有效波高H0与不同时刻的风速Ut作为SVR模型的输入信息，设计了23组数值试验（M10—M32），深入分析不同的风浪输入信息组合对有效波高预测技巧的影响。表4列出了利用当前有效波高H0和不同时刻的风速Ut作为输入信息（H0和U-3、H0和U0、H0和U3）的试验结果，可以看出将H0和U3作为输入信息对有效波高的预测技巧最高，其未来3 h有效波高预测的RMSE、R、IA分别为0.179、0.963、0.977，对未来12 h有效波高仍然具备一定的预测能力，但预报误差变化特征表明，随着预测时效的延长预测误差也随之增加。此外，综合表2、表3和表4的误差统计结果可见，使用风浪组合作为输入信息的预测结果更接近实测有效波高。

为进一步提高对12 h和24 h有效波高的预测能力，本文考虑将预测时刻的风速作为SVR模型的输入信息，进而分别针对12 h和24 h有效波高预测目标独立训练其最优预测参数。根据输入的预测风速时效不同，将数值试验分为当前有效波高H0和预测时刻前6 h风速、当前有效波高H0和预测时刻前3 h风速、当前有效波高H0和预测时刻风速共3类数值试验。误差统计结果表明（见表5）。对12 h和24 h的有效波高预测技巧最高的是M25和M28，其中12 h有效波高预测的RMSE、R、IA分别为0.295、0.892、0.929，也就是说采用当前有效波高H0和预测时刻前3 h风速作为输入信息，其12 h和24 h有效波高预报技巧达到最高。如表5所示，该方法对12 h和24 h有效波高预测误差基本相当，也就是说该方法对24 h有效波高预测结果可用。

为进一步评估多组输入信息对有效波高预测效果的影响，本文在上述数值试验的基础上，将8个变量Hi和Ui（i=-3、-2、-1和0）均作为SVR模型的输入信息，设计了3组试验（M30、M31、M32）。实验结果表明（见表6），在认为所有输入信息都具有同等重要性的前提下，同时引入多个输入信息的并不能有效提升预测效果，反而增加了SVR模型的计算时间。

表4 利用当前有效波高H0和不同时刻的风速Ut作为输入信息的预测试验的有效波高预测误差

表5 输入当前有效波高H0和不同预测时刻的风速Ut作为输入信息的预测试验的有效波高预测误差

表6 使用8个变量作为输入信息的误差

6 结论

本文利用PSO算法，建立了基于SVR的有效波高短期预测模型，并开展了不同风浪输入信息组合对有效波高预测影响的敏感性试验。通过优化径向基核函数的参数γ和模型中的惩罚参数C，以及采用最优化风浪组合方案作为模型输入信息，开展了对渤海海域近岸有效波高3 h、6 h、12 h和24 h的预测可靠性研究。试验结果表明：风速是影响有效波高预测最重要的因素，利用当前风速信息能够准确实现对3 h和6 h有效波高的预测，但随着预测时效增加，12 h和24 h预测准确性迅速降低；当前有效波高仅对3 h有效波高预测具备一定预测技巧，其影响作用不可忽视；同时引入当前有效波高和不同时刻的风速作为输入信息可有效改善预测能力，当预测时效延长至12 h后，将预测风速作为模型的输入信息，可有效提高12 h和24 h的有效波高预测准确性；此外，若模型输入信息与预测对象不存在显著的相关，多个输入信息不能有效提高模型的预测能力。综上所述，SVR模型对于小样本数据具有较高的学习能力和适应能力，为复杂地形近岸海域有效波高短期预测提供了一种有效的机器学习方法，可在海洋环境业务保障中推广应用。