台风“Megi”(2010)过程中海浪的特征及其对大气海洋的影响研究
徐海波,杜华栋,项杰,操俊伟
(1.国防科技大学气象海洋学院,江苏南京211101;2.中国人民解放军66199部队,北京100043;3.太原卫星发射中心,山西太原 030000)
1 引言
台风过程通常会伴随着强烈的海气相互作用过程,在海面产生高达数十米的海浪,对沿海地区海洋工程和人民的生产生活造成巨大影响。许富祥等[1]通过统计资料表明,仅南海海域,平均每年出现有效波高高于6 m海浪的平均次数就达7.6次。此外,许多研究表明,海浪对台风和海洋环流的发展演变均有重要的动力和热力影响,因此,台风过程中对于海浪的准确预报,显得尤为重要。
关于海浪的数值模拟,近20 a内有了巨大的进展,至今已经发展到第三代海浪谱模式,例如:WAM(Wave Model)模 式[2]、WAVEWATCH III 模 式[3]、TOMAWAC[4]和近岸海浪数值模型(SimulatingWAves Nearshore,SWAN)模式[5]等。第三代海浪模式是一个直接表示和海浪发展相关物理过程的全海浪谱模式,可以给出海浪状态完整的二维特征。得益于此,近年来,许多学者做了大量有意义的研究。例如,Chu等[6]使用WAVEWATCH III模式,分析了台风“Muifa”(2004)过程中海浪的分布特征,并研究了不同的台风移动速度、台风强度和海底地形对台风海浪谱的影响。陈希等[7]和Ou等[8]使用SWAN模式,在充分考虑海浪相关物理过程的基础上,研究了台湾岛附近海域台风浪的特征,模拟的海浪结果与实况吻合较好。以上研究均表明,SWAN模式能够较好模拟台风过程中海浪的发展变化情况。
台风过程中产生的巨浪同时会对大气和海洋产生影响。正如Zhang等[9]指出,一方面,台风中巨大的海浪会加大海气的动量通量输送,削弱海表面风速。另一方面,由于海表面粗糙度的增加,海气热力学相互作用也会加强,产生更大的热量和湿度通量输送,因此海浪模式会改善风速、通量和海洋混合的预报[10-14]。Olabarrieta等[15]通过模拟一次飓风过程指出,海浪改变了海面的粗糙度,改善了风速、海流的模拟效果,耦合海浪之后,海表面平均潜热通量较未耦合模式有了明显的增加,同时也明确了海浪与大气边界层的相互作用在台风风速预报和描述海面状态中的重要性。此外,Zambon等[14]也发现,耦合模式提高了海表面温度(Sea Surface Temper-ature,SST)的模拟效果。类似的,Wada等[12]也通过一组耦合对比试验指出,破碎的表面波的引入,能更好地模拟台风“海棠”(2005)的SST。台风过程中,海浪还会与海流产生强烈的相互作用。刘娜等[16]的研究指出,海流模式与海浪模式的耦合提高了有效波高的模拟效果,这表明,对于台风中海气相互作用的研究,一个全物理过程耦合的耦合系统是有必要的。
尽管对于台风浪的研究已经有了很大的进展,但存在一些不足:比如,前人的研究多是基于单个个例模拟,对于全新的个例,不确定是否能够得到类似的结论;此外,海浪在影响海气热量输送方面,鲜有定量研究。本文意在弥补这些不足,并通过一个未被研究的个例台风“Megi”(2010)来探究海浪在台风过程中的作用。本文将首先验证耦合模式对海浪的模拟效果,其次分析海浪的参数以及分布特征,最后讨论海浪对台风以及海洋的影响。
2 数据与方法
2.1 数据介绍
本文中天气预报模式(Weather Research and Forecasting,WRF)模式初始场和边界条件资料为美国国家环境预报中心(National Centers for Environmental Prediction,NCEP)发布的 1°×1°再分析资料。海洋环流初始场由垂直混合坐标模式(Hybrid Coordinate Ocean Model,HYCOM)再分析场(ftp://ftp.hycom.org)插值得到。海浪模式的初始场采用美国国家海洋和大气管理局(National Oceanic and Atmospheric Administration,NOAA)提供的海浪历史数据(ftp://polar.ncep.noaa.gov/pub/history/waves/)。台风最佳路径和最大风速数据使用的是美国海军联合台风预警中心(U.S.Navy Joint Typhoon Warning Center,JTWC)发布的数据。SST卫星观测资料来自NOAA提供的海表面温度卫星观测资料(http://oceanwatch.pfeg.noaa.gov/thredds/dodsC/satellite)。本文验证海浪模拟效果时用的Janson-1/Jason-2卫星高度计产品由Aviso+(https://www.aviso.altimetry.fr/)制作和发布,作为Ssalto地面处理模块的一部分。
2.2 模式简介
本文使用的模式由Warner等[17]开发,并被许多学者广泛应用[14-15,18]。关于海洋-大气-海浪耦合(Coupled Ocean-Atmosphere-Wave-Sediment Transport,COAWST)模式的系统介绍可以参考文献[19],此处,本文重点介绍海浪与大气和海洋环流的耦合过程。
如图1所示,COAWST系统由3个子模式组成,分别是区域大气模式WRF、海洋环流模式(Regional Ocean Modeling System,ROMS)和海浪模式SWAN,各子模式之间通过耦合器(Model Coupling Toolkit,MCT)交换数据。WRF模式为非静力、准可压的大气模式,采用Arakawa C网格计算,耦合过程中给ROMS模式输出海面风场、热量以及辐射通量,给SWAN模式输出海面风场;ROMS模式为自由表面、跟随地形的海洋数值模式,其在水平方向上采用Arakawa C网格进行有限差分近似,耦合过程中,给大气模式输出SST作为大气模式的底部边界条件,同时给海浪模式输入流速、海面高度和地形;SWAN模式为海浪谱模式,可以模拟海面风驱动波的产生和传播,模拟折射、衍射、波-波相互作用等各个物理过程,在耦合过程中,其可以给ROMS和WRF模式输出海面波高、波长等波浪参数,此外还可以给ROMS模式输出波向、表面和底部周期、波浪破碎百分比、波浪能量耗散等等。海浪模式求解波作用谱平衡方程:
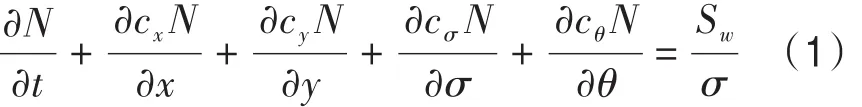
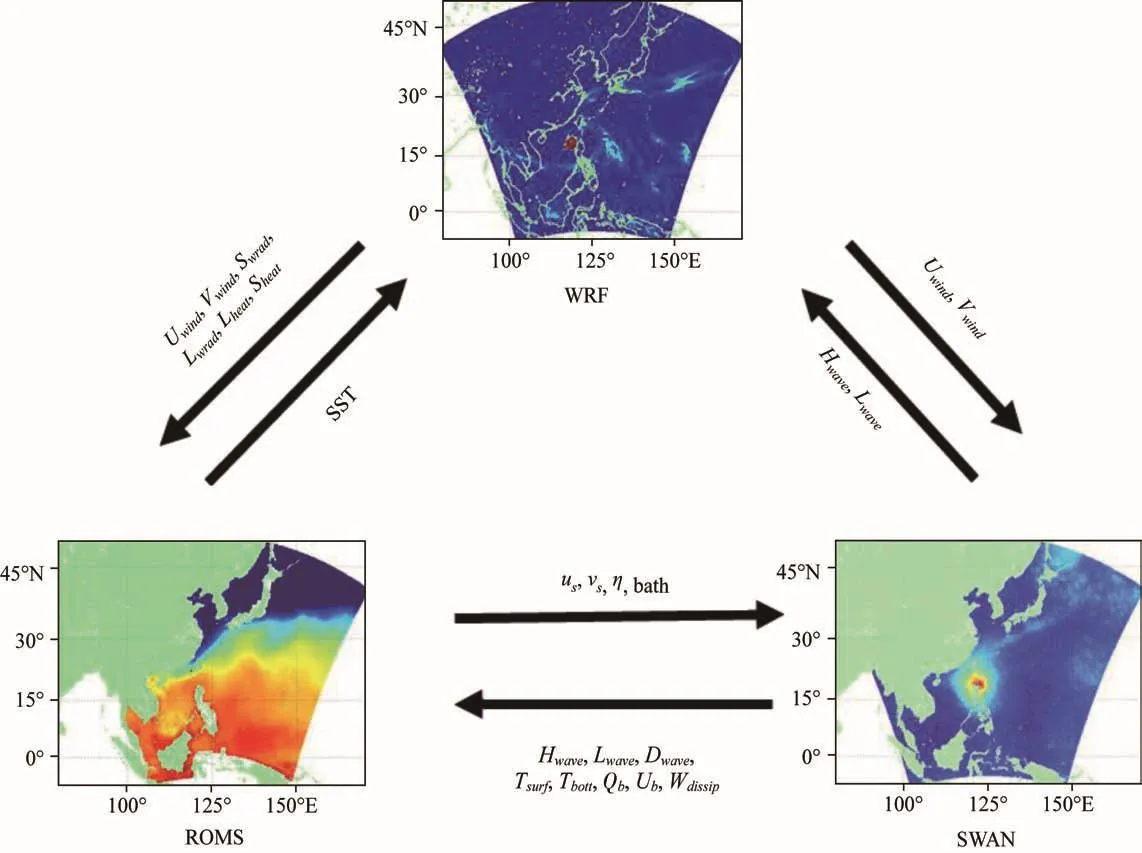
图1 COAWST系统示意图
式中:N(σ,θ,x,y,t)为波作用谱,σ 为相对角频率(对海流移动观测的参考系内观测的角度),θ是与波峰垂直的方向,x和y坐标空间(可以在球坐标系和笛卡尔坐标系中表达),t为时间。cx和cy为x和y方向的群速,意义为在地理空间,上式左端第四项表示由于深度的变化和在频率空间中以cσ群速流动的流的变化导致的相对频率的变化。第五项表示可以使在方向空间以cθ为群速的深度和流诱导折射存在。Sw表示动密度的源和汇项。
2.2.1 海洋环流-海浪耦合
浪流耦合过程中,一方面,海洋环流会对波浪的演变和发展产生影响,流模式根据浪模式提供的参数,计算得出流速、水位等海洋要素,并传递给浪模式,浪模式进而进行下一阶段的计算,如此循环直至模拟结束。在SWAN模式波作用谱平衡方程中,表示由于水深和背景流场引起的频率迁移,N表示水深和背景流导致的波浪折射,其中:
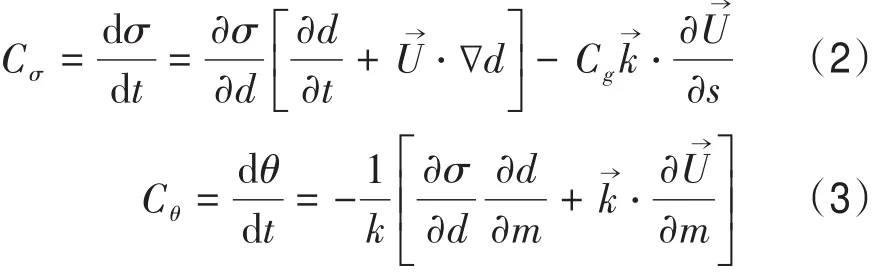
式中:Cσ和Cθ分别为在频率空间以及在方向空间波的群速度,d为水深,U⇀为流速矢量。
另一方面,海浪也对海洋环流有着不可忽略的影响,一般可以用辐射应力梯度或者梯度力描述这一作用[20-21]。辐射应力表示波浪运动过程中对周围流体产生的作用力,ROMS中使用的三维辐射应力表达式为:


式中:u、v、Ω为3个方向的平均速度分量,Hz是格点厚度,f是科氏力参数,ρ和ρ0分别为海水总密度和相对密度,ν是分子粘性。这样,海浪的作用得以通过辐射应力的形式在海洋环流求解中体现出来。
2.2.2 海浪-大气耦合
台风过程中,海表面强大的风场会在海面驱动强盛的波浪场,耦合模式中WRF将10 m风速U10实时传输至海浪谱模式,进行海浪的计算。海浪谱模式的源汇项表达式为:
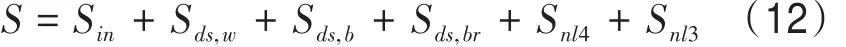
式中:风能输入项Sin=A+BE(σ,θ),两个部分分别为线性增长项和指数增长项。在耦合模式中,风能项使用的是大气模式输入的10 m风速U10,然后转换为摩擦速度分别计算线性增长项和指数增长项,摩擦速度U*的计算公式为:

CD表示拖曳系数:
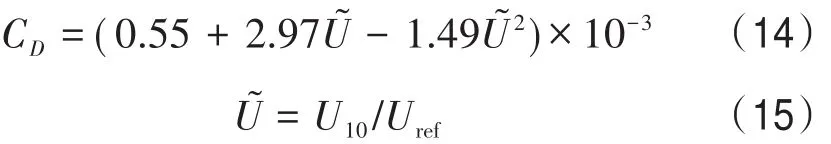
式中:Uref为参考风速。以上表明,WRF模式将模拟的海面10 m风速传递给海浪模式,海浪模式计算风能输入项,求解海浪波作用谱平衡方程。
表面强盛的波浪场也显著改变了海表状态,影响海气界面通量的计算与交换,这种影响通过海面粗糙度来体现。WRF中表面动量Fm、热量Fh和湿度Fq的计算表达式如下:
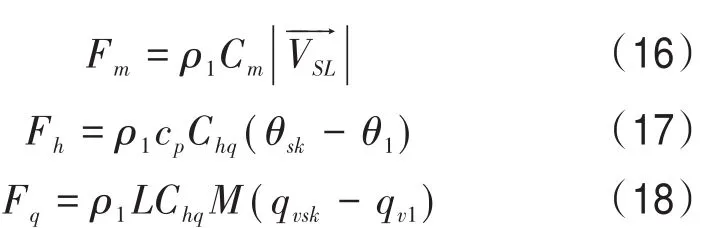
式中:Cm为动量交换系数、Chq为热通量和水汽通量交换系数,表达式如下:
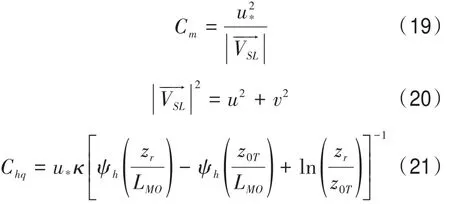
式中:zr为观测高度,z0T为温度粗糙度长度,LMO是Monin-Obukhov长度。
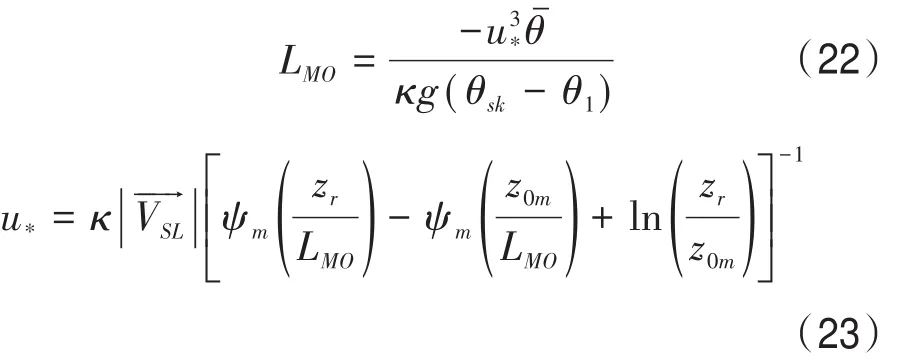
式中:z0m为动力粗糙度长度。
海面的波浪改变海面动力粗糙度长度,影响摩擦速度u*,进而影响海气界面的通量输送。在耦合模式中,浪模式根据大气模式输入的风场,计算波浪的增长,浪模式进而将计算所得的浪参数传递给大气模式,大气模式据此计算海表面的粗糙度。在COAWST系统中,Warner等[17]对WRF模式进行了一些修订,为了更好的体现海浪的影响,使其在计算海洋上方大气底部应力的时候增强底部动力粗糙度,将WRF中使用的Charnock[22]方案替换为Taylor等[23]方案:
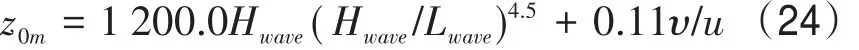
式中:Hwave为有效波高,Lwave为平均波长,υ为粘性应力。
2.3 模式配置
本文共进行了3组数值试验,分别是单独大气模式进行的UNCOUP、海洋-大气-海浪耦合全物理过程耦合的COUP1试验和海洋-大气耦合的COUP2试验。各组试验的模拟时间均为2010年10月17日06时—2010年10月22日18时(世界时,下同),各子模式采用相同的15 km网格,SWAN模式角度分辨率Δθ=10°,频率为0.04~1.0 Hz,f(n+1)/f(n)=1.1。由于模拟初始时刻台风强度很大,NCEP初始场数据分辨率较低,气旋强度小,因此本试验采用添加bogus涡旋的方案,在模拟初始时刻12 h前的初始场添加与实况一致的热带气旋,由WRF模式单独运行12 h,所得结果作为3组试验大气模式的初始场。ROMS模式中的水平对流方案采用三阶迎风方案,垂直对流方案采用四阶中心方案,底部边界层闭合方案采用Sherwood方案,压力梯度计算采用Shchpetkin方案,垂直湍流混合方案采用一般长度尺度混合方案,模式边界条件采用闭合边界条件。
在SWAN模式中,使用第三代海浪模拟方案,风场输入、白冠破碎采用Komen等[24]的方案,浅水中深度诱导破碎系数取为α=1.01,β=0.73,底部摩擦采取Madsen等[25]的方案,海浪传播方案采用BSBT方案。
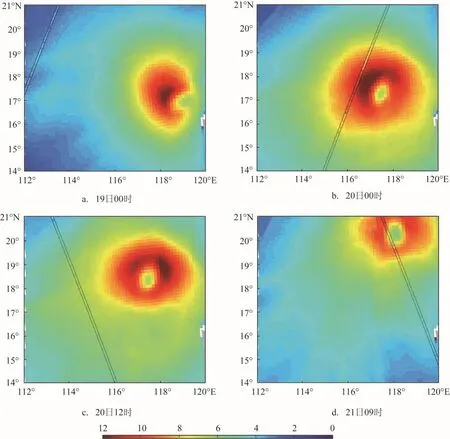
图2 海面有效波高值(单位:m,底色为模拟结果、黑色实线内部为Jason-1/Jason-2卫星高度计资料求出的有效波高)
3 模拟结果验证
此次台风过程中,COAWST系统较好模拟出了大气、海洋和海浪的动力和热力状态,对于大气和海洋模拟的结果的验证,已经在其他文章中发表[19],因此本文仅做简要介绍,此处将重点对比海浪模拟结果。
在台风过程中,由于深海处海浪浮标等观测装置的缺乏,通常只能用卫星高度计资料作为实况参考[26-27],图2为Jason-1/Jason-2卫星高度计资料反演出的海浪有效波高产品与模拟结果的对比图。图中清楚地表现出了COAWST系统对海浪的模拟效果。在图2中的4个时次中,卫星轨迹刚好经过台风上方,如图所示,在台风边缘和台风中心附近,SWAN模式都较准确模拟出了海浪的有效波高大小和分布特征,因此保证了本文对海浪模拟结果分析的可靠性。
4 结果分析
4.1 海浪特征分析
4.1.1 有效波高
有效波高为统计海浪特征的最常用的指标。根据海浪谱,有效波高可以通过下式计算:
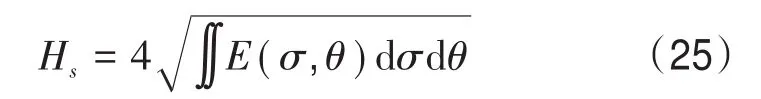
式中:E(σ,θ)为二维海浪方差谱,σ 为频率,θ为方向。
图3 a和图4 a分别表示了18日21时和20日09时西北太平洋部分海域的有效波高分布情况。由此两张图可以看出,台风过程中,产生了高达12 m以上的海浪。海浪的空间分布也呈现较大的不对称性。在台风移动方向右前方,有效波高大于其他位置的波高,在台风中心附近,呈现低水位。18日21时,除了台风中心附近较大海域的海浪高值区域,在吕宋岛以东至台湾岛以东一带,也有4 m左右的海浪,这是由于台风在东菲律宾海移动时产生的涌浪传播至北方。
4.1.2 波长
波长指一个周期内,海浪传播的距离。根据海浪谱,平均波长可以通过下式计算:
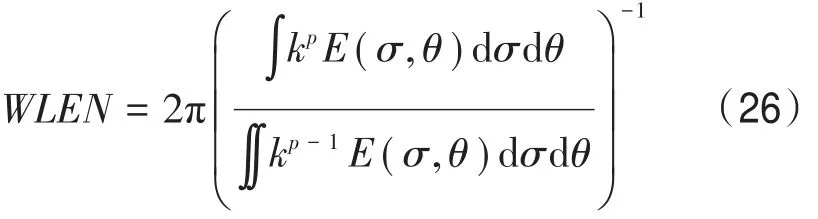
式中:p为能量参数,取为1。
图3 b和图4 b为18日21时和20日09时海浪的平均波长分布情况。在台风中心附近,波浪的平均波长呈现为大值区,最大平均波长在140 m以上。18日21时,由于涌浪的传播,吕宋岛东至台湾岛以东一带呈现出较大的平均波长特征,特别在台湾岛以东,最大波长也达到了140 m以上。在20日09时,吕宋岛东部向北传播的涌浪的耗散,台风在南海上产生的涌浪沿东北方向传播至台湾岛东部海域,也产生了140 m左右的平均波长。
4.1.3 周期
周期定义为两个相邻的波峰之间跨零点的时间差。平均周期可以通过下式计算:
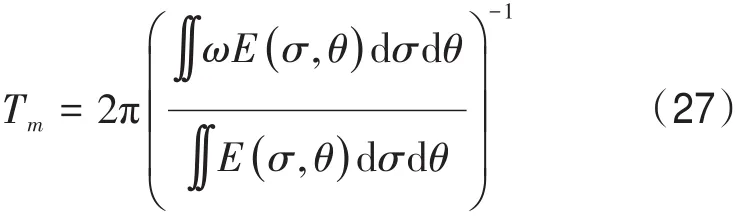
式中:ω为绝对频率。
图 3 c、3d和图 4 c、4d分别为18日21时和20日09时海浪的平均周期和谱峰周期。台风的存在使海面产生了较大周期的海浪,最大平均周期在12 s左右,谱峰周期略大于平均周期。在18日21时和20日09时两个时次,台湾岛东部至吕宋岛东部海域周期分布差异较大,前一个时次主要是台风在吕宋岛东时产生的涌浪占主导,而后一个时次主要是台风在南海时产生的涌浪占主导,且最大谱峰周期达到了16 s以上。
4.1.4 波向
计算波平均方向时,本文使用的是如下的表达式:
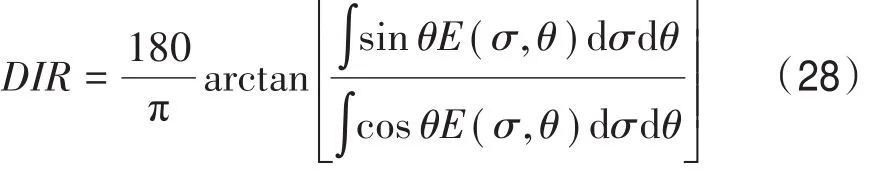
谱峰方向则直接将海浪方差谱沿频率积分,取峰值时的角度即可:
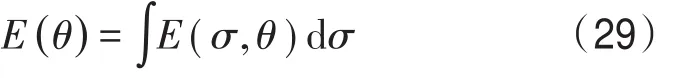
图 3 e、3f和图 4 e、4f分别为18日21时和20日09时海浪的平均波向和谱峰波向。18日21时,台风中心附近的波向呈逆时针旋转,在南海其他区域,波浪总体向西南方向传播,而在东菲律宾海域,海浪主要向北传播。谱峰波向与平均波向接近,但是相对于平均波向,向右偏转了15°~30°。20日09时,随着台风中心的北上,南海区域的海浪传播方向有了较大的变化,总体呈现逆时针旋转,此外,台风在南海产生的东北向的风浪穿过台湾岛与吕宋岛之间,向西北太平洋海域传播,并与台风在东菲律宾海产生的涌浪相遇。这一特征在谱峰波向上表现得更明显,这也与上文分析的波高、周期、波长分布的特征相吻合。
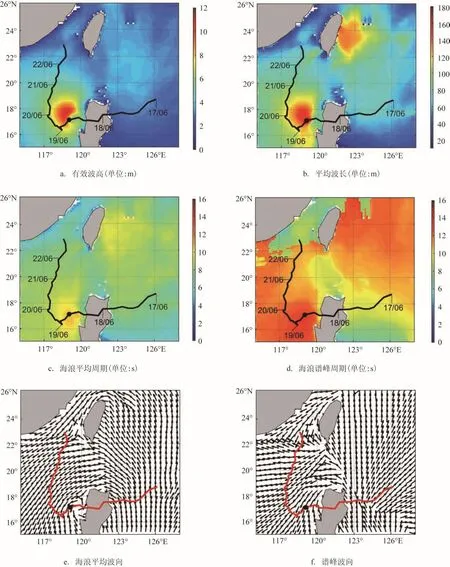
图3 18日21时SWAN模式模拟结果(图中黑色圆点为当前时刻台风中心的位置)
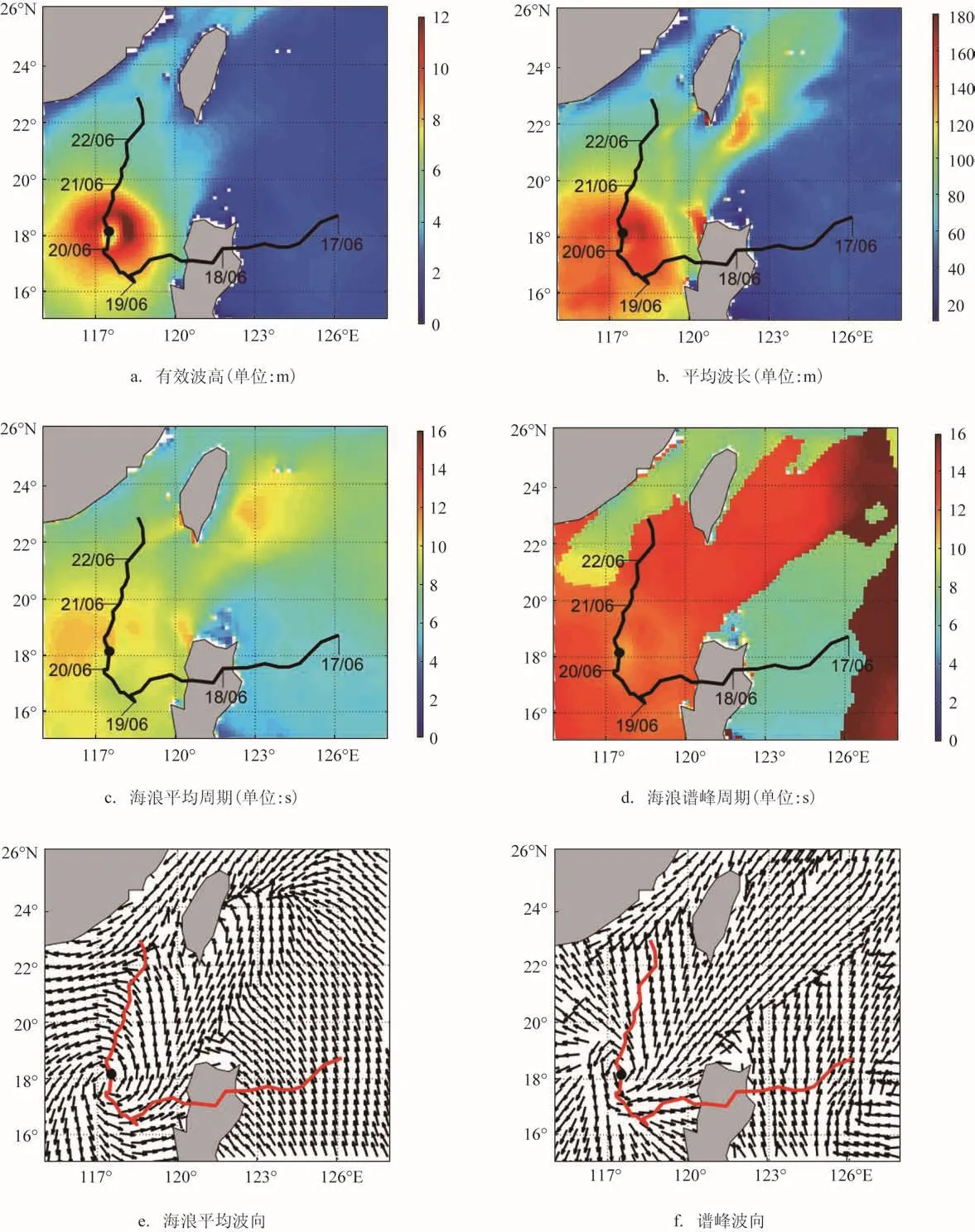
图4 20日09时SWAN模式模拟结果(图中黑色圆点为当前时刻台风中心的位置)
4.2 海浪对台风的影响
海浪作为台风与海洋相互作用的交界面,对海洋与大气之间的动量热量输送有着重要的影响。通过对比海-气-浪耦合结果与海-气耦合结果,发现对比单独运行大气模式,COUP1和COUP2试验都显著提高了预报效果;但是从最低海面气压和最大风速角度看,COUP1和COUP2体现出的海浪对台风强度影响较小(见图5)。
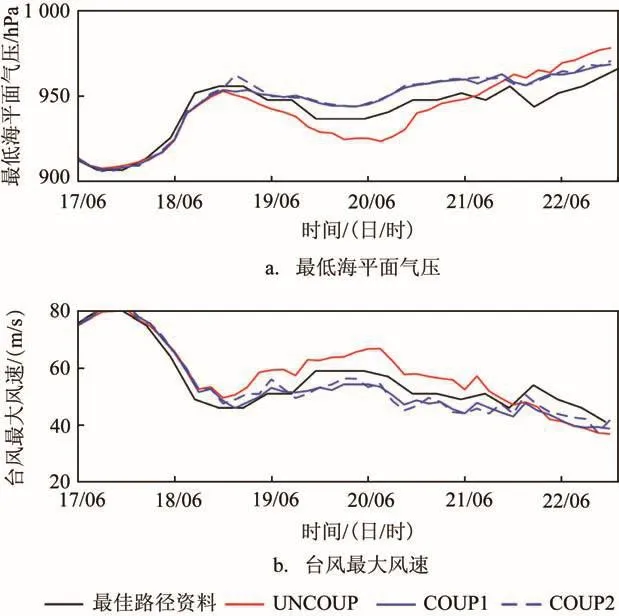
图5 最佳路径资料、UNCOUP、COUP1、COUP2试验的最低海平面气压和台风最大风速随时间变化图
图6 为COUP1试验与COUP2试验海面风场的差值和海面潜热通量的差值。海浪的加入使得模拟台风中心和后部的风速减小了3~5 m/s,同时,分析两者模拟的潜热通量可得,海浪的加入使得台风内核区域的潜热通量增大了100 W/m2,在外围区域则有增大有减小。增大的潜热通量输送尽管没有改变台风强度,但是调节了台风中心周围的风速分布,对台风外围的风场结构也产生了一定的影响。图6c为耦合海浪后台风内核区域潜热通量变化趋势图。由图中可知,考虑海浪后,内核区域潜热通量总体呈上升趋势,最大增大率达到了15%,表明海浪过程的耦合对于台风的潜热通量的准确计算很重要。
4.3 海浪对海洋的影响
在台风过程中,台风产生的剧烈的海浪会与海流产生相互作用,也会对海洋的混合产生影响。图7为COUP1和COUP2试验对SST模拟的对比图。在20日12时,两者模拟的SST产生了明显的差异,未耦合海浪的COUP2试验模拟的SST降温幅度小于COUP1试验。对比同样时刻的观测资料表明,COUP1试验模拟的SST较好地重现了台风过后的海面降温过程,而COUP1试验降温响应之所以较为滞后,可能是由于海浪产生了更强的混合,如Wada等[12]所指出,海浪破碎影响的引入加强了海洋混合层的混合,产生了更接近实况的SST分布特征。此外,对比COUP1和COUP2模拟的海洋环流场,COUP1试验模拟海流较COUP2有较大的偏移,特别是在19日15时,海浪的加入使台风北部的流场明显北偏,加强的向北对流一方面加强了冷海水的向北输送,另一方面改变了三维的环流场,可能对海洋的垂直对流、垂直混合产生影响。
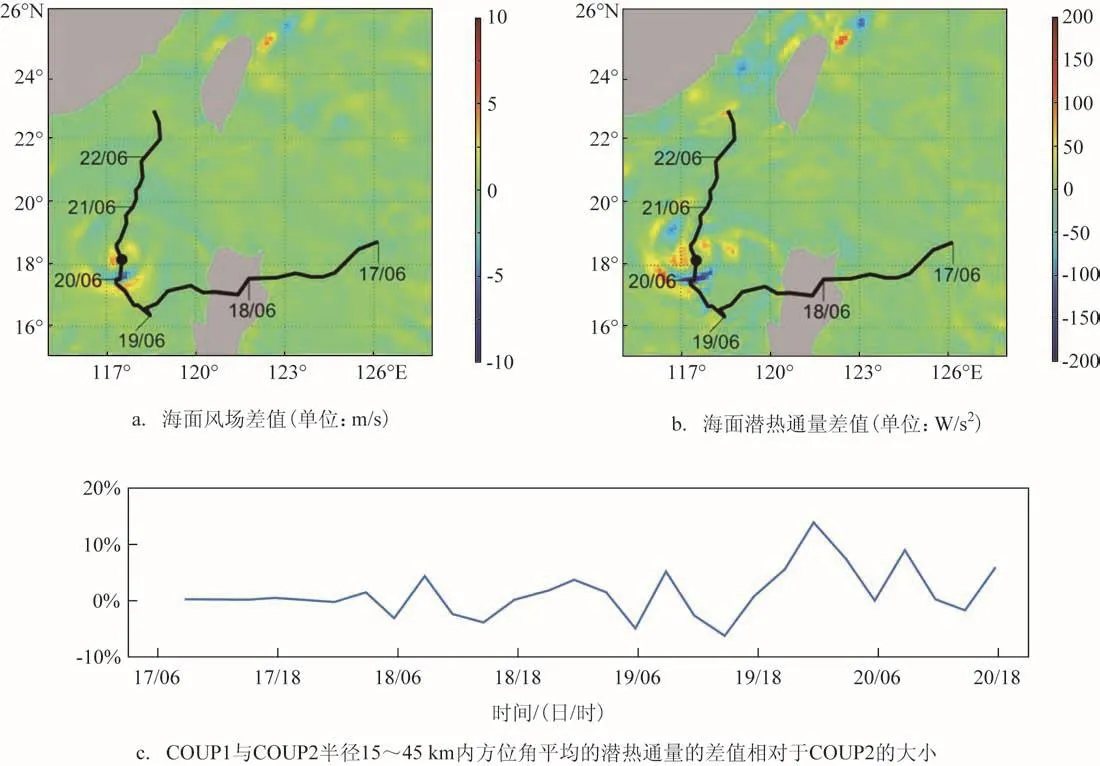
图6 20日09时COUP1试验与COUP2试验海面风场与海面潜热通量差值
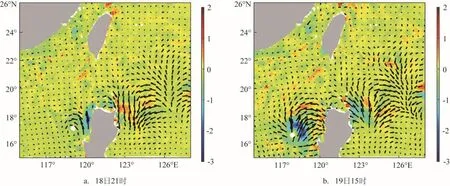
图8 COUP1与COUP2试验的海水流速矢量差(箭头)和SST之差(填色)
5 结论
本文利用COAWST海洋-大气-和海浪耦合系统,模拟了2010年10月17日06时—22日18时台风“Megi”(2010)的发展演变过程,并通过与最佳路径资料、卫星资料反演产品对比,验证了模拟结果的可靠性。在此基础上,本文分析了台风过程中海浪的分布特征,以及海浪对台风和海流的影响,主要结论如下:
(1)对于台风过程中海浪的有效波高和海浪的波长、周期与波向,分析结果表明,台风过程中,产生了巨大的海浪,有效波高高达12 m以上,在移动方向的右前方,有效波高大于其他位置,台风中心呈现低水位特征,这与前人做的一些关于海浪的观测和模拟试验[11,28]相符合;台风中心周围的海浪有着最大的波长,在前进方向右前侧更明显;涌浪的传播也导致在台湾岛东岸产生了较长波长的海浪。通过分析台风的平均周期、谱峰周期、平均波向和谱峰波向,发现谱峰周期和平均周期的分布很相似,但周期大小略高于平均周期;谱峰波向相比平均波向向右偏了约15°~30°,这一特征与Chen等[26]通过分析海浪谱特征得出的结论相一致,另外模式较好模拟出了涌浪的传播方向,在台风西移和北上两个阶段,涌浪方向发生了改变。
(2)关于海浪对台风的影响,对比试验结果分析表明,海浪模式的加入没有明显改变台风的最低海平面气压和台风最大风速,但是对水平风场却起到了调节作用,使得模拟台风中心和后部的风速有了略微的减小,正如Chen等[11]通过雷达资料分析指出的那样,可能是由于海面对表面风场的拖曳作用。此外,本文还对比了两组试验的潜热通量的大小,发现考虑海浪后,由于海面粗糙度的增加,内核区域潜热通量总体呈增大趋势,最大增大率达到了15%,这也体现出了耦合模式在台风准确预报中的重要性。
(3)对台风过程中台风浪与海流产生强烈的相互作用的对比试验结果分析表明,海浪的加入加剧了海洋混合,产生了更大的海面降温,更接近于实况值,与Wada等[12]的研究结论类似。此外,海浪的加入还改变了海流的方向,这也可能是影响SST分布变化的原因之一。

