基于代理辅助分层粒子群算法的页岩气藏压裂参数优化
姚 军, 李志豪, 孙 海
(中国石油大学(华东)石油工程学院,山东青岛 266580)
页岩气藏属于致密性气藏,孔渗性质差,常规开采难度大,必须采用水力压裂措施进行储层改造,其两个关键的技术是水平井和水力压裂。压裂技术在实际油气藏实施很成功,然而在其设计优化上做的工作还不足。据统计大约有三分之一的压裂都没有实现预期的产能[1],主要原因是裂缝和油藏特征的复杂性以及大量设计变量。研究问题主要包括水平井位置选择、井间距调整、裂缝条数与裂缝半长的设计问题。对于压裂优化这个“黑箱”问题,亟需建立一套完整的优化设计体系来指导现场施工作业。从井参数到裂缝参数设计会耗费大量的时间,选择合适的优化方法尤为重要。目前已有较多学者对裂缝参数优化进行了研究,主要是基于无梯度算法和代理模型的使用。Ma等[2]对比分析了SPSA、GA和CMA-ES算法优化井位置和压裂段数,充分展现了无梯度算法的实用性。代理模型在传统油气藏优化里应用广泛,如产能优化[3]、水驱[4]、气驱[5]、化学驱[6]、蒸汽辅助重力采油[7]和历史拟合[8]等;非常规油气藏里代理模型应用也很多,Gorucu等[9]基于ANN构建了致密气藏代理模型,前过程预测生产结果,逆过程反求最优参数;Wilson等[10]将原模型简化为内外拥有不同孔渗性质的简化物理模型,在此基础上进行优化模拟,大大提高了优化效率;Al-mudhafar等[11]基于二次多项式模型和径向基模型在固定裂缝条数前提下优化了单井时裂缝的其他参数,结论是径向基网络模型得到的结果更加准确。当前研究存在的不足在于,多数学者都是在保持其他参数不变的情况下,对某几个裂缝参数进行敏感性分析,而不是从整体的角度去优化,得到的结果往往不是最优的;无梯度算法固然灵活,但在保证全局搜索时一定程度上降低了寻优速度。笔者建立页岩气藏水平井流动模型,将代理辅助分层粒子群算法(SHPSO)应用到井工厂模式下,从水平井空间位置到裂缝的条数、间距和半长,以净现值最大化为目标优选压裂参数。
1 页岩气藏模型与求解函数
1.1 页岩气藏模型
基于商业数值模拟软件ECLIPSE构建页岩气藏水平井流动数学模型。将气水两相、多重介质模型、非达西流动、水平井摩阻和吸附解吸因素考虑到模型中。使用多重介质模型表征从基质到裂缝的暂态流动,如图1所示,Vp表示孔隙体积。

图1 多重介质模型示意图
不同于致密气藏,页岩气藏富含有机质,以吸附态形式存在于干酪根和黏土颗粒表面的气体比例可多达60%[12]。本文中采用Langmuir等温吸附公式描述吸附解吸效应,对应的方程为

(1)
式中,θ为尺度系数;ps为标况压力,1.013×105Pa;R为通用气体常数;Ts为标况温度,273 K;pc为当前压力,Pa;VL为Langmuir体积,m3/kg;pL为Langmuir压力,Pa。
此外,压裂后的页岩气藏,气体在高导流水力裂缝中的流动为高速非达西流,采用Forchheimer方程进行描述,即

(2)
其中
式中,q为体积流量,m3/s;k为岩石渗透率,10-3μm2;Kr为相对渗透率;A为流动区域面积,m3;μ为流体黏度,Pa·s;ρ为流体密度,kg/m3;β为Forchheimer参数;φ为孔隙度;S为饱和度;a、b、c、d为常数。
页岩气藏压裂后,水力裂缝激活天然裂缝,从而形成储层改造体积(stimulated reservoir volume,SRV),极大改善了水力裂缝周边区域的孔渗性质。本文中SRV定义为围绕水力裂缝外圈网格部分,如图2灰色区域所示。

图2 SRV示意图
1.2 求解函数
本文中采用净现值(net present value,NPV)为适应度评价函数。模型涉及到的变量主要有12个,分别为井1的坐标x和y、横向井间距L1、纵向井间距L2、裂缝条数Ni(i=1~4)、裂缝半长Lxfi,
u=argmaxJ.
(3)
其中
lmin≤ui≤lmax,i=1,2,…,12.
式中,J为净现值;Qg为年产气量,m3;Qw为年产水量,m3;rg为天然气价格,元/m3;rw为水处理费用,元/m3;b为折扣率;m为总井数;n为生产总时间段数;Δt为折扣时间段,a;O为每口井每天的操作费用,元;Cw为钻竖直井段成本,元;N为裂缝条数;Cf为单条裂缝造价,元;Lw为水平井长度,m;Cp为单位长度水平井造价,元/m;ui为第i个变量;lmin和lmax分别为第i个变量的下限和上限值。
水平井分布示意图如图3所示。

图3 水平井分布示意图
2 基于代理辅助的分层粒子群算法
代理辅助分层粒子群(SHPSO)算法由Yu等[13]首次提出,在解决多维问题快速寻优时表现良好。本文中将该算法运用到页岩气产能优化。该算法将代理模型与粒子群算法结合,既保留了粒子群算法的全局寻优能力,又融入了代理模型的预测功能,相比普通智能算法拥有更高的寻优速度和精度。
2.1 径向基网络模型
代理模型是指通过训练一复杂度低的数学模型,替代原有模型进行设计优化[14]。常用的代理模型有多项式响应面法、克里金方法、径向基函数法和神经网络方法等。本文中使用径向基网络方法(RBFNN)构建代理模型。RBFNN是一种3层神经网络,包括输入层、隐含层和输出层。其基本思想是用径向基作为隐单元的“基”构成隐含层空间,这样就可以将输入矢量直接映射到隐空间,而不需要像人工神经网络那样进行权连接,结构示意图如图4所示。本文中输入层为1.2节中的12个参数变量,隐含层为转化后的高维线性可分空间,输出层为净现值。RBFNN具有唯一最佳逼近特性,且无局部极小问题存在,具有很强的输入输出映射功能,学习算法简单方便。
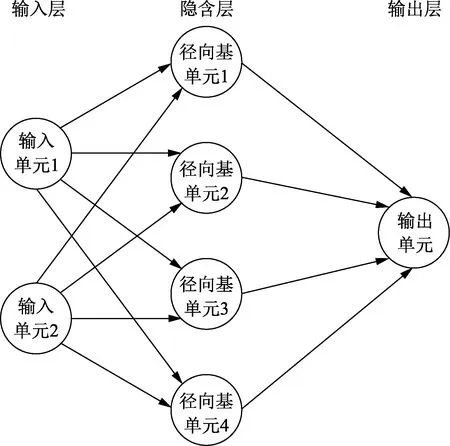
图4 RBFNN示意图
2.2 拉丁超立方抽样方法
经典抽样方法主要包含蒙特卡洛抽样和拉丁超立方抽样方法(Latin hypercube sampling,LHS)。蒙特卡洛抽样是完全随机的,在求解空间内样本可以落在任何位置,而且样本常落于高分布概率区域,当执行迭代次数较少时会产生聚集问题。与蒙特卡洛方法相比,拉丁超立方抽样被设计成通过较少次数的抽样来准确地重建输入分布,其关键是对输入概率分布进行分层,可以随机而且系统地分布在求解空间内,所取得的样本更具有代表性。
本文中使用拉丁超立方抽样方法进行采样,并与随机采样(random sampling,RS)方法得到的数据分布进行对比,结果如图5所示。以二维空间、样本点为10为例,相比随机采样,拉丁超立方抽样方法采样每行每列有且仅有一个样本点,保证了样本散落均匀,能更广泛地覆盖变量空间。

图5 LHS采样与RS采样对比
2.3 SHPSO算法流程
SHPSO是基于传统粒子群(PSO)算法与社会学习粒子群算法SLPSO分层组合进行优化的。基本公式与传统PSO类似,包含速度更新公式与位置更新公式。与传统PSO不同的是其考虑了RBF代理模型辅助优化而产生的最优值sr,即RBFNN寻找到的最优解。如果sr对应的真实值优于全局最优值sg,则速度公式改为用sr代替sg求解。同理,在更新位置全局最优sg和个体最优sp时也采用对应的sr,基本公式为

(4)
其中
式中,x为粒子位置;v为粒子速度;r为0到1的随机数;c1=c2=2.05。
内部SLPSO用于求解RBFNN模型的最优解,外部PSO基于更新的样本库迭代求解。其基础框架如图6所示。

图6 SHPSO循环示意图
样本库的更新来源为RBFNN求得的最优解以及外层PSO中优于sp的个体。算法的详细流程如图7所示。

图7 SHPSO步骤示意图
3 应用实例
4口井分布于长2 500 m、宽1 500 m、厚60 m的页岩气藏中,各井坐标分别由井1的x、y坐标以及横向井间距L1、纵向井间距L2确定。裂缝等距分布在长1 100 m的水平井内,间距是裂缝条数的函数,模型如图3所示。
模型基础数据参照Ma等[2]历史拟合过的Barnett页岩,初始气藏压力为20.6 MPa,井底流压为3.5 MPa,生产年限为20 a,天然裂缝渗透率为0.000 1×10-3μm2,天然裂缝孔隙度为0.000 05,水力裂缝导流能力为0.3×10-3μm2·m,Langmuir压力为4.48 MPa,Langmuir体积为0.002 7 m3/kg,SRV区域渗透率为0.000 5×10-3μm2;基质渗透率为(0.000 1~0.000 3)×10-3μm2,基质孔隙度为0.04~0.08,孔渗性质示意图如图8所示。

图8 基质孔隙度与渗透率分布
受模型限制,变量取值范围及经济参数取值[15]:裂缝条数为10~40,裂缝半长为100~300 m,横向井间距为1 100~1 500 m,纵向井间距为200~800 m,井1的横坐标为10~200 m,纵坐标为100~900 m。气体价格为0.791元/m3,折扣率为12.5%,竖直段钻井成本为140万元,井日常操作费用为420元。
裂缝造价参照冯其红等[16]回归分析得到的计算公式,

(5)
式中,Lxf为裂缝半长,m。
3.1 传统单因素
针对裂缝半长、裂缝条数、横向和纵向井间距进行传统单因素分析。为简化计算,分析裂缝半长与条数时仅取单井进行模拟,平均基质孔隙度为0.050 7,平均基质渗透率为0.000 148×10-3μm2。图9为不同裂缝条数下净现值与裂缝半长的关系曲线。由图9可知,在不同裂缝条数下,净现值均随着裂缝半长的增大而先增后减,最优半长为230 m。这主要是由于半长值较小时,增加半长带来的收益高于成本;随着半长增加对压裂设备性能要求提高,成本上升。对比不同裂缝条数的曲线可知,在相同裂缝半长的条件下,随着裂缝条数的增加,净现值先增加后减少,且最优裂缝条数为26条。此时单条裂缝的控制区域可达最优。
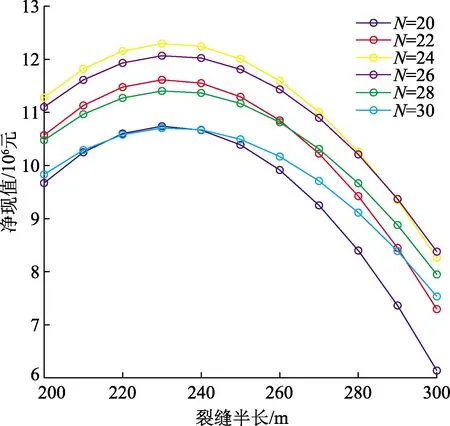
图9 净现值与裂缝半长的关系
固定裂缝条数N=26、半长Lxf=230 m和井1坐标(x=50 m,y=400 m)条件下,分别求得均质和非均质时净现值对横、纵向井间距的关系曲线,如图10所示。均质条件下净现值与横、纵向井间距呈相同的变化趋势,均为先增大后减小。这是由于间距过小时井间干扰严重;间距过大时,气井生产受边界影响变大。非均质条件下,净现值与纵向井间距变化规律不变,而随横向井间距的减小而增大,考虑其原因是受地层非均质的影响,使布井倾向于丰度更高的位置。

图10 净现值与井间距的关系
3.2 基于SHPSO的参数优化
采用数值模拟软件ECLIPSE与MATLAB结合,基于SHPSO对裂缝半长、裂缝条数、井坐标和横、纵向井距进行优化。基本参数设置:外层粒子群种群数为50,允许最大调用ECLIPSE次数为250次;内层粒子群种群数为100,最大迭代数为500,终止误差为1×10-6,初始样本库数量设为80。图11为样本库随算法迭代而更新、排序及筛选的过程。
由图11可知,首先基于LHS生成了80个遍布变量空间的随机解,其净现值均值为2.40×107元;随迭代样本库数量增加至125、154、187、212、250,对应净现值均值分别为2.96×107、3.13×107、3.41×107、3.57×107和3.74×107元。样本库的更新来源只有2个,即SLPSO寻得的最优解sr和外层粒子大于个体最优的解,均为筛选对比之后的变量组合。由散落的样本数据可知,随样本库数量的增加,新增的解逐步收敛至最优值。

图11 样本选取示意图
对于RBFNN模型训练集为每代更新后的前50个样本,测试集为全体变量集合。一般来讲,使用的训练样本数越多,RBFNN模型越准确;同时存在一阈值,超过该值会出现过拟合现象。样本库随迭代实时更新,令训练集始终保持为50个,既可以避免过拟合,同时也保证了训练精度和质量。
裂缝分布如图12所示。求解结果为井1坐标x=40 m,y=700 m,4口井裂缝条数分别为26、24、27、25,裂缝半长分别为230、220、230和230 m,横向井间距为1 110 m,纵向井间距为530 m,最优解为5.781×107元。分别比较单因素分析与整体分析、SHPSO与普通智能算法对比的结果。

图12 裂缝分布
3.2.1 与传统单因素分析对比
单因素分析是在固定其他参数时得到某一变量对整体净现值的影响,在变量维度小时有效可靠;但当多口井进行组合优化时,变量维数增多,若再以非整体的思想去分析问题,得到的结论不一定是合理的,尤其在非均质条件下优化布井问题时,井位的选择需要结合每口井的裂缝参数去优化考虑。根据最终结果可知,并非每口井参数都相同;当4口井条数均为26,半长均为230 m时的净现值为5.541×107元,相比之下最优解提高了4.3%(约240万元)。可见,从成本的角度来讲,整体优化要比单因素分析结果更合理。
3.2.2 与普通智能算法对比
以调用ECLIPSE次数为横坐标,纵坐标为当前全局最优。分别采用标准PSO和SHPSO对模型进行求解,结果如图13所示。

图13 SHPSO与PSO对比寻优曲线
相比PSO算法,在调用ECLIPSE次数相同的前提下SHPSO算法能更快地捕捉到最优值的邻域,而且最终结果更优。SHPSO平均最优净现值为5.74×107元,PSO平均最优净现值为5.37×107元,同比提高了6.89%。拉丁超立方抽样数设为80,可以最大限度地遍历变量空间;RBFNN辅助预测可以为算法提供潜在最优方向。程序绝大部分时间用于ECLIPSE求解产能,相比之下代理模型的训练和寻优可以忽略不计,故将运行时间看作与调用次数成正比。虽然智能算法可以有效避免求解梯度问题,但对于多维数、单次运行时间长的情形难以有效解决,而代理模型的结合很好地弥补了这个缺陷。相比之下,SHPSO比普通智能算法拥有更快的收敛速度和结果准确度。
4 结 论
(1)MATLAB与ECLIPSE的结合使用实现了自动寻求最优参数组合。优化方法采用基于代理模型辅助优化的分层粒子群算法SHPSO,相比普通智能算法,SHPSO拥有更快的收敛速度。
(2)相比传统单因素分析,从整体的角度去优化结果更加合理。井工厂模式同步压裂并非每口井简单地复制叠加,单井的设计参数不能照搬到井工厂模式下,而是需要作为一个整体去优化考虑,这样才能更符合现场实际。

