迭代法在高加筋土边坡设计中的应用

李宏阶 江平 许斌 李红涛

摘要：以湖北某山区高填方工程为例，运用迭代法计算边坡最不利滑动面及筋带设计拉力，并根据简化Bishops法进行最不利滑动面的复核运算;运用FLAC3D中内置的强度折减法对边坡未折减前及折减后的边坡水平位移、垂直位移、总体位移和剪应变进行对比分析;最后与实际监测数据进行对比分析，研究了折减法在高加筋土边坡设计中的应用，为加筋技术在土边坡工程中的应用提供参考。

Abstract： Taking a high-fill project in a mountainous area in Hubei Province as an example， the iterative method is used to calculate the most unfavorable sliding surface and the reinforcement design strength of the slope， and the review operation of the most unfavorable sliding surface is performed according to the simplified Bishops method; the strength reduction method built in FLAC3D is used to the horizontal displacement， vertical displacement， overall displacement and shear strain of the slope before and after the reduction of the slope are compared and analyzed; finally， the analysis is compared with the actual monitoring data to study the application of reduction method in the design of high-reinforced soil slopes and provide reference for the application of reinforced technology in soil slope engineering.

关键词：加筋土边坡;强度折减法;稳定分析;有限元;迭代法

Key words： reinforced soil slope;strength reduction method;stability analysis;finite element;iterative method

中图分类号：U416.1                                      文献标识码：A                                  文章编号：1006-4311（2020）20-0222-04

0  引言

在工程建设中，由于加筋土边坡具备施工速度快、工期较短，结构技术简单、施工容易方便，造价较低、经济效益好等特点，现已经广泛应用于各种填方边坡[1～3]。

目前常采用的研究方法主要有极限平衡法和有限单元法等[4～5]。这些方法未能全面考虑土体内部的应力应变，根据现有设计规范《土工合成材料应用技术规范》及《公路土工合成材料应用技术规范》，其方法为先根据未加筋时的最小安全系数和设计要求的安全系数，计算所需的总筋材拉力，再根据拉力值设计筋材。在现有实际工程中，经常使用卵石、碎石土等无粘性或低粘性土作为填料，由于填料黏聚力C值較低，而填料黏聚力对边坡安全系数影响非常显著，计算得到的到最小安全系数对应的滑面则会较浅，若直接按该滑面进行设计，容易出现设计拉力偏低的情况从而影响工程安全[6～9]。因此本文探讨了迭代法在边坡稳定可靠度分析中的应用。

1  加筋土边坡稳定性方法

1.1 极限平衡法

极限平衡法是根据静力平衡原理分析边坡各种破坏模式下的受力状态，以边坡滑体上的抗滑力和下滑力之间的关系来评价边坡的稳定性。工程中常用的分析方法有多种，主要要瑞典条方法、简化毕肖普（Bishop）法、简布（Janbu）法等，设计中主要为简化毕肖普（Bishop）法，该法考虑了土条侧面的作用力，并假定各土条底部滑动面上的抗滑安全系数均相同，由于推导过程中忽略了条间切向力，计算结果较为合理。

1.2 强度折减法

随着计算机技术的日益完善，强度折减法在边坡稳定性分析中得到了广泛的应用和发展。所谓强度折减，是指在理想弹塑性有限元计算中将岩土体抗剪强度参数逐渐降低，直至其失稳破坏。根据弹塑性破坏区域得到破坏滑动面（塑性应变和位移突变的地带），可得到边坡的强度储备安全系数ω。

强度折减法稳定系数的定义在本质上与极限平衡条分法安全系数的定义是一致的，都属于强度储备系数。它们所表示的是整个滑面的安全系数（即滑面的平均安全系数），而不是某个应力点的安全系数。

计算时，首先选取初始折减系数ω，将土体强度参数进行折减，用折减后的参数进行有限元静力计算，若土体仍处于稳定状态，则再增加折减系数直到边坡处于极限状态为止，此时的折减系数即为边坡的稳定安全系数。

2  迭代法确定最不利滑动面及筋带设计拉力

由于计算软件功能的完善，边坡稳定性的计算越来越准确，可以采用迭代法进行计算，具体步骤如下：

步骤1：根据设计坡面确定拟加筋高度范围;

步骤2：采用三角形受力分配确定各个加筋区的受力比例;

步骤3：选定一个初始滑动面，可以固定圆弧的出口和入口，自动搜索最危险滑面，并采用不平衡推力法计算该滑面的剩余下滑力N1;

步骤4：根据分配比例分配该下滑力T1=N1;

步骤5：为简化计算，将各个分区的加筋设成一道加筋，将其抗拉力设置为分配下滑力，并自动搜索最危险滑动面及安全系数F1;

步骤6：计算该滑面的剩余下滑力N2，并令T2=N1+N2，重新按步骤4、5计算，得到安全系数F2;

步骤7：根据T1对应的F1及T2对应的F2按线性插值计算设计安全系数F所对应的T，反复迭代即可求出设计安全系数Fs对应的最不利滑动面及筋带拉力值Ts。

3  实例分析

3.1 工程概况

工程场地位于湖北山区，由于山地多而平地少，为解决用地问题而回填形成平台，最大平台高差约为40m。填料拟采用场区挖方边坡的岩土体，对该区岩土体进行了大样剪切试验，密实度不小于94%时，材料的内摩擦角为35.5°由于边坡较高，其设计安全系数为1.35。

3.2 设计拉力值计算

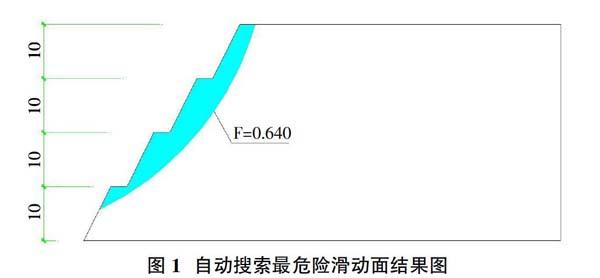
为节省用地及保证安全，填土取γ=20g/cm3，c=0kPa，φ=35°，设计剖面按10m一级，坡率为1：0.5，每级平台宽2m，采用简化Bishop法搜索最小滑动面，计算得到如图1所示的计算结果。

计算结果表明，计算得到的最小安全系数滑动面不能客观地反映边坡最不利滑动面。因此按迭代法计算最不利滑动面及筋带设计拉力。

工程按每10m一个加筋区，加筋区为4个，其受力按三角形分配，即1/16、3/16、5/16、7/16。根据迭代法，初始指定一个离坡顶外侧距离10m为入口的滑面，计算得到其安全系数为0.955，其剩余下滑力为T1=N1=1672kN/m，将其分配后计算得到F1=1.307，计算该滑面的剩余下滑力N2=1096kN/m，T2=1672+1096=2768kN/m，计算得到最小安全系数为F1=1.488，插值计算得到Fs对应的T=1933kN，计算得到最小安全系数为1.350，满足设计要求，无需再次进行迭代。计算过程如表1所示。

■

3.3 加筋带布置

加筋带按60cm一层，每个区可以布置17道，第一区单层拉力为7.1kN，第二区单层拉力为21.3kN，第三区单层拉力为35.5kN，第四区单层拉力为49.7kN，考虑材料的折减系数，第一区采用HDPE90，第二区采用HDPE130，第三区采用HDPE130，第四区采用HDPE170，具体布置如图2所示。

3.4 稳定性复核

3.4.1 简化Bishops法

根据上节的加筋方案，考虑实际情况，对该剖面采用Geo-Slop进行了复核计算，结果如图3所示。

计算表明，最不利滑动面与设计最不利滑动面相近，加筋后的安全系数为1.372，略大于设计要求安全系数1.35，达到设计要求且经济合理。

3.4.2 强度折减法

对填方边坡建立了有限元模型，边坡土单元和地基土单元均用四结點实体单元，土工格栅采用杆单元。网格剖分后该模型包含46062个节点，56409个单元，模型顶宽为52m，高约45m。具体如图4所示。

通过计算，在未折减前，其结果如图5-图8所示。

根据强度折减理论，当强度折减系数ω=1.34时，该边坡接近极限平衡状态，其结果如图9-图12所示。

计算结果表明，未折减前该高填土边坡的稳定性较好，边坡前缘及墙内外填土交界处有一定数值的塑性应变，但量值较小，不会影响其整体稳定性。

强度折减后，首先在墙内回填土下部出现塑性应变，其分布范围较强度折减前明显的增大，剪应变值由3%增大到10%，说明该边坡在强度折减后很有可能发生墙体拉裂破坏，最终导致整体破坏的发生。

3.5 监测结果

该边坡于2017年建成，随后进行了1个水文年的变形监测，坡顶变形监测结果如图13所示。

监测结果表明，由于土体固结尚未完成，存在一定变形，但其变形值较小，满足规范要求。

4  小结

本文通过湖北某山区高填方工程的实际算例，研究了迭代法在高加筋边坡设计中的应用。采用简化Bishops法和强度折减法进行稳定性复核，运用FLAC3D中内置的强度折减法对边坡水平位移、垂直位移、总体位移和剪应变进行对比分析，证明了迭代法在高加筋土边坡设计中的可行性;通过变形监测数据的分析证明了高加筋土边坡在边坡处理中的实用性。

参考文献：

[1]孟宝华，邓宇，章宁，王宁.加筋土柔性结构在深厚填方边坡治理工程中的应用[J].土工基础，2018，32（04）：379-384.

[2]郑争锋，邹贤尧，陈志杰.加筋土高边坡变形沉降量与监测周期预测[J].绿色科技，2019（06）：172-175.

[3]介玉新，周诗博，郭政豪，陈杰.平台分级对加筋土边坡稳定性的影响研究[J].工程地质学报，2018，26（05）：1178-1187.

[4]苏立海，吕燕，冀勋高，杨勇，贡文献.强度折减法在加筋土边坡安全系数验算中的应用[J].人民长江，2018，49（S2）：285-290.

[5]许雅琦，祝启坤.强度折减法在加筋土高边坡稳定分析中的应用[J].岩土工程技术，2015，29（04）：192-196.

[6]张琬，许强，陈建峰，薛剑峰.加筋土边坡筋材拉力分布与分区[J].交通运输工程学报，2017，17（06）：28-35.

[7]吴培元.加筋土边坡合理布筋方式研究[D].兰州交通大学，2017.

[8]顾婕，张孟喜.基于强度折减理论的加筋土边坡稳定性分析[J].上海大学学报（自然科学版），2019，25（06）：990-1002.

[9]赵建红.高填方加筋土边坡受力和变形试验研究[J].公路与汽运，2010（05）：103-106.