Extremal Functions for Adams Inequalities in Dimension Four

LI Xiaomeng*

1 School of Information,Huaibei Normal University,Huaibei 235000,China.

2 Department of Mathematics,Renmin University of China,Beijing 100872,China.

Abstract.Let Ω ⊂R4 be a smooth bounded domain,be the usual Sobolev space. For any positive integer ℓ,λℓ(Ω)is the ℓ-th eigenvalue of the bi-Laplacian operator.Definewhere is eigenfunction space associated with λi(Ω). denotes the orthogonal complement of Eℓ in For 0≤α＜λℓ+1(Ω),we define a norm byforIn this paper,using the blow-up analysis,we prove the following Adams inequalities moreover,the above supremum can be attained by a function with‖u0‖2,α=1.This result extends that of Yang(J.Differential Equations,2015),and complements that of Lu and Yang(Adv. Math. 2009)and Nguyen(arXiv:1701.08249,2017).

Key Words:Adams inequality;Trudinger-Moser inequality;extremal function;blow-up analysis.

1 Introduction and main result

Trudinger-Moser inequalities play important roles in analysis and geometry.There are two interesting subjects in the study of Trudinger-Moser inequalities:one is what the best constant is,the other is the existence of extremal functions.The research on sharp constants was initiated by Yudovich[1],Pohozaev[2]and Trudinger[3].Later Moser[4]found the best constant:ifthen

where Ω is an open subset of Rn(n≥2)with finite Lebesgue measure,ωn-1is the measure of the unit sphere in Rn;moreover,ifβ＞β0,the integrals in(1.1)are still finite,but the supremum is infinite.The sharp constants for higher order derivatives of Moser’s inequality was due to Adams[5]. For any fixed positive integerm,letthe space of functions havingm-th continuous derivatives and compact support. To state Adams’result,we use the symbol ∇muto denote them-th order gradient foru.Precisely

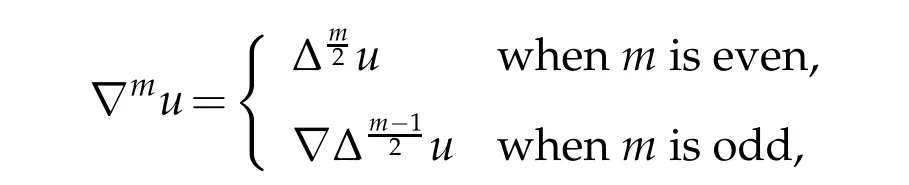
where ∇and Δ denote the usual gradient and the Laplacian operators.Adams proved that ifβ≤β(n,m)and 0＜m＜n,then

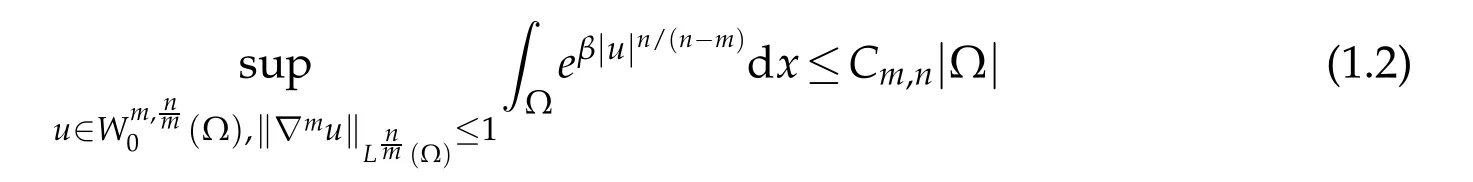
for some constantCm,n,where

Moreover,β(n,m)is the best constant in the sense that ifβ＞β(n,m),then the supremum in(1.2)is infinite.The manifold version of Adams inequality was obtained by Fontana[6].Extremal functions for(1.1)were first found by Carleson and Chang[7]when Ω is the unit ball in Rn. This result was then extended by Flucher[8]to a general domain Ω⊂R2,and by Lin[9]to a bounded smooth domain Ω⊂Rn(n≥2).

In 2004,it was proved by Adimurthi and Druet[10]that for anyα,0≤α＜λ1(Ω),there holds

and the supremum is infinit forα≥λ1(Ω),whereλ1(Ω)is the first eigenvalue of the Laplacian operator with respect to Dirichlet boundary condition. The inequality(1.3)was generalized by Yang[11]to high dimension,by Lu and Yang[12]and J.Zhu[13]to the versions involvingLpnorms,by Souza and dóO[14,15]and Ruf[16]and Li and Ruf[17]to the whole Euclidean space,by Tintarev[18]and Yang[19]to the following form:

for any 0≤α＜λ1(Ω).In particular,Yang[19]proved that for 0≤α＜λℓ+1(Ω),the extremal function for(1.4)exists,where ℓ is a positive integer andλℓdenotes the ℓ-th eigenvalue of the Laplacian operator with the Dirichlet boundary condition.The singular version of(1.4)was considered by Yang and Zhu[20],Li and Yang[21],and the author[22]in Rn(n≥2).For other works on Trudinger-Moser inequalities,we refer the reader to[23–28]and the references therein.

The study of Trudinger-Moser inequalities on Riemannian manifolds was initiated by Aubin[29]and Cherrier[30,31].Much work has also been done in this direction,see for examples[32–38].

Let us come back to the Adams inequality in dimension four.Namely

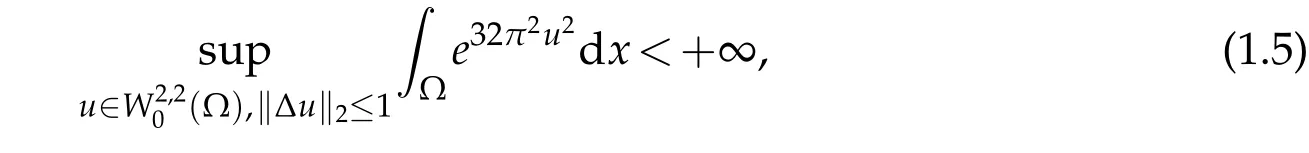
where Ω ⊂R4is a smooth bounded domain.For anyα:0≤α＜λ1(Ω),it was proved by Lu and Yang[39]that

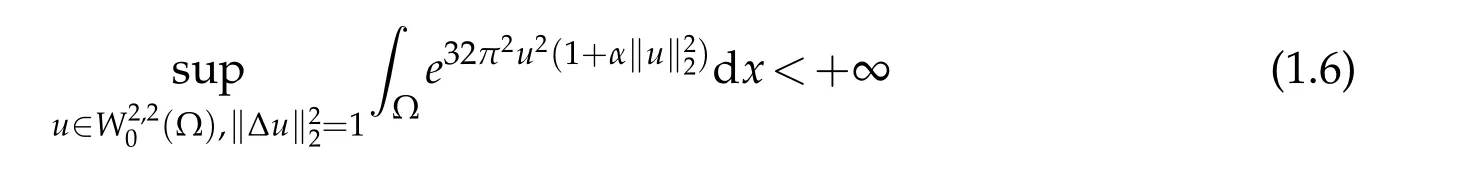
and the supremum is infinite whenα≥λ1(Ω).Here,by definition,

The extremal function for supremum(1.6)was obtained forαsufficiently small. This result is recently strengthened by Nguyen[40]to the following form:

for 0 ≤α＜λ1(Ω),and the above supremum can be achieved by applying the blow-up analysis method.Motivated by the work[19],we shall improve(1.7)to the case involving higher order eigenvalues.Note that the Dirichlet boundary problem

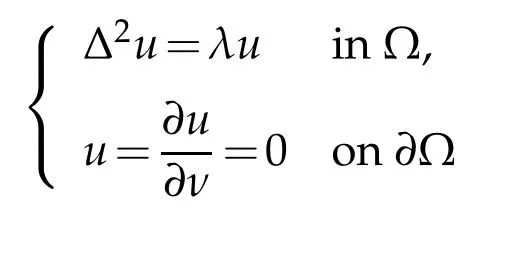
possessesa sequence of eigenvalues 0＜λ1(Ω)＜···＜λi(Ω)＜λi+1(Ω)＜···.It is known thatλi(Ω)→∞asi→∞,see for example[41,Section 6.3].The corresponding eigenfunction space can be written as

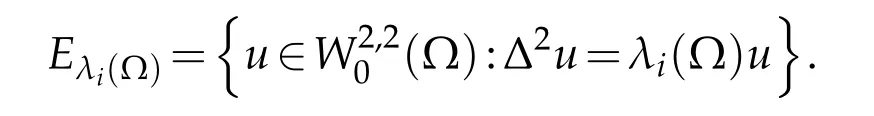
For any positive integer ℓ,we set

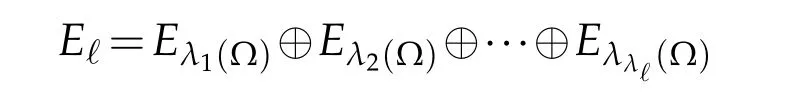
and

Clearlyis a real Hilbert space when it is equipped with the inner product

According to[41,Theorem 9.31],each eigenfunction spacehas finite dimension.Suppose dimand(eij)(1≤j≤ni,1≤i≤ℓ)be the basis ofEℓ.Then

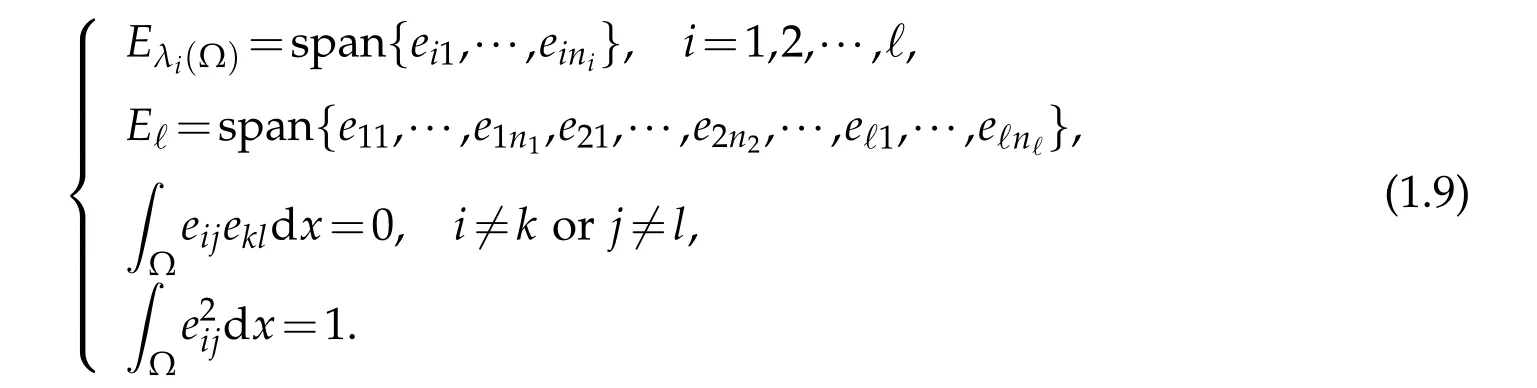
Similar as in[19],we define

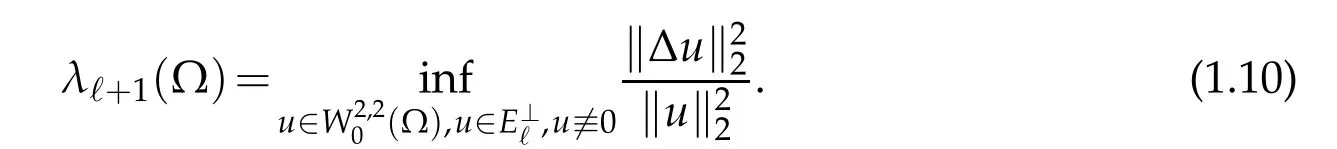
Ifsatisfiesthen we denote

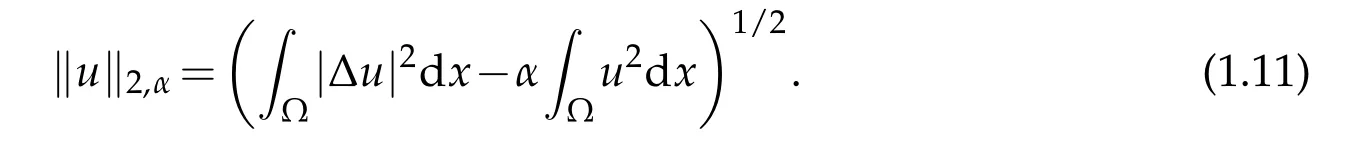
In this paper,we prove the following:

Theorem 1.1.LetΩbe a smooth bounded domain inR4,ℓbe a positive integer, and λℓ+1(Ω)be defined as in(1.8)and(1.10)respectively.Then for any0≤α＜λℓ+1(Ω),the supremum

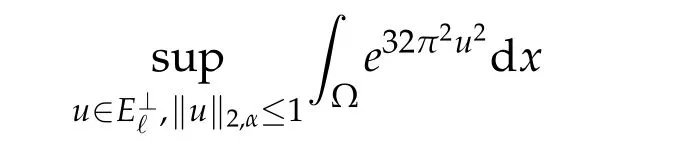
can be attained by some functionwith

Obviously Theorem 1.1 extends a result of Yang[19,Theorem 2]and includes[40,Theorem 1.3]as a special case.The proof of Theorem 1.1 is based on blow-up analysis,which is also used in[39,40,42].

The remaining part of this paper is organized as follows:In section 2,we state some results which are crucial in the subsequent analysis;We prove the existence of subcritical maximizers in section 3 and study the asymptotic behavior of these maximizers in section 4;In section 5,we will give upper bound estimates of the functionalunder the assumption of blow-up analysis;In section 6,we construct a sequence of test functions to complete the proof of Theorem 1.1.

2 Preliminary results

In this section,we state some preliminaries which would bring a great convenience during our calculation.

LetG:Ω×Ω →R be the Green function of Δ2under the Dirichlet condition.That is,for everyy∈Ω,the mappingsatisfies(in the sense of distribution)

All functionssatisfying Δ2u=f(u)can be written as

wherefdoes not depend onu.Now,we collect a property for derivatives ofG,see for example[43].There existsC＞0 such that

and

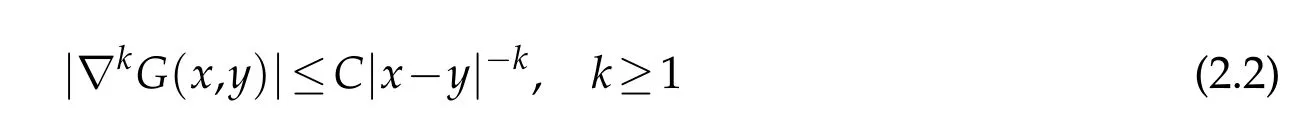
for allx,y∈Ω,We next recall the Pohozaev identity due to Mitidieri[44].

Lemma 2.1.LetΩ′be a smooth bounded domain inR4Δ2u=f(u)inΩ′.Then we have for any y∈R4,

where=v and ν is the normal outward derivative of x on ∂Ω′.

Similar to[39,40],we have the following Lion’s type result.Namely

Lemma 2.2.Letbe a sequence of functions and0≤α＜λℓ+1(Ω)Then for any

3 Extremals for subcritical Adams inequalities

In this section,we shall prove that for any 0 ＜∈＜32π2,there exists some functionu∈∈withsuch that

where‖·‖2,αis defined as in(1.11).This is based on a direct method in calculus of variations.Compared with[40],we will derive a different Euler-Lagrange equation on which some new analysis is performed.

For any 0＜∈＜32π2,we take a sequence of functionssatisfying that

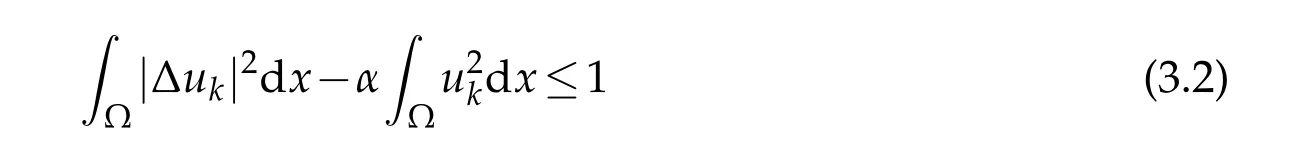
and that

It follows from(3.2)and 0≤α＜λℓ+1(Ω)thatukis bounded inThen there exists some functionsuch that up to a subsequence

Sincewe have

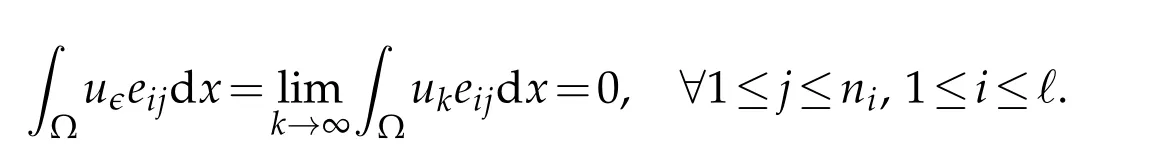
HenceBy Lemma 2.2,we haveis bounded inLr(Ω)for somer＞1.Therefore

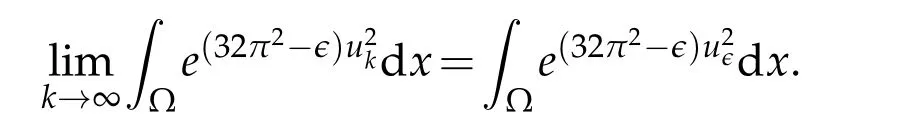
This together with(3.3)immediately leads to(3.1). Obviously the supremum(3.1)is strictly greater than the volume of Ω.ThusIfwe have

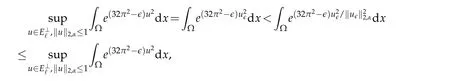
which is a contradiction.Then we obtain‖u∈‖2,α=1.

A straightforward calculation shows thatu∈satisfies the following Euler-Lagrange equation:

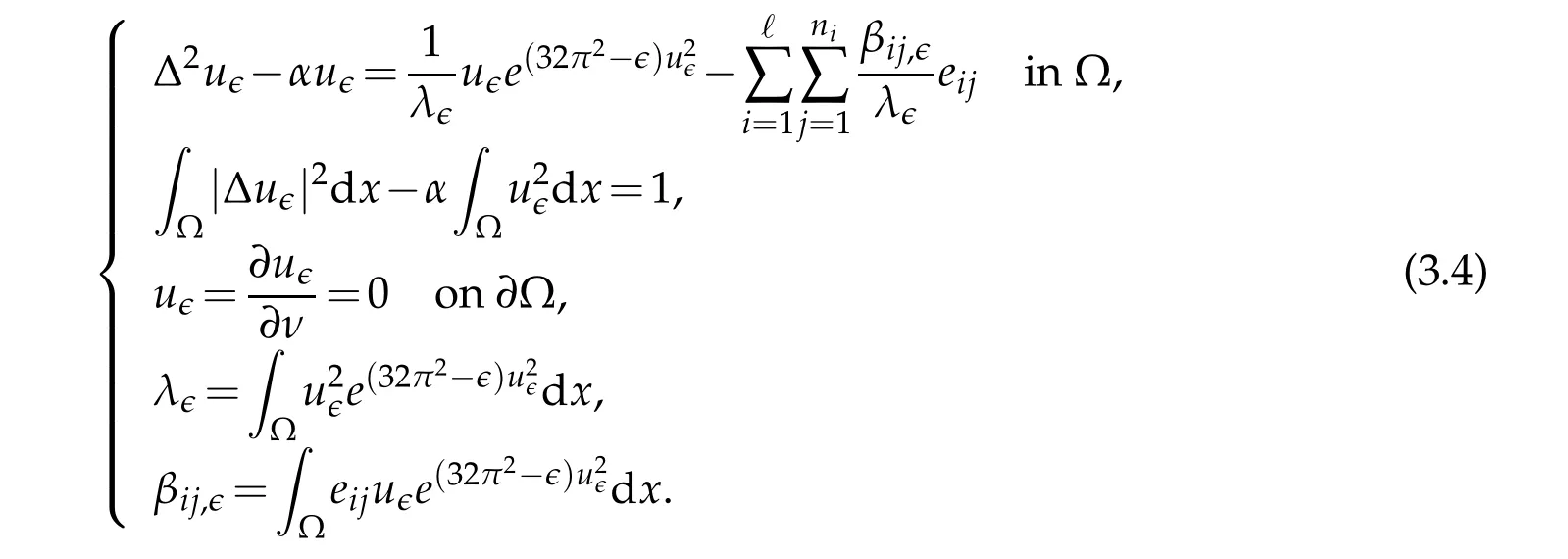
Applying the standard regularity theory to(3.4),we obtainSinceu∈is bounded inwe can assume without loss of generality,

Sincethen

Hence we get

DenoteIfc∈is bounded,thenis bounded inL∞(Ω). Clearlyis also bounded inL∞(Ω). Thus for anywith‖u‖2,α≤1,we have by(3.1)and the Lebesgue dominated convergence theorem

This implies that

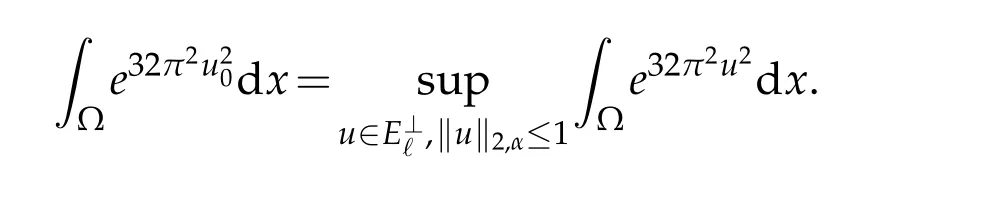
Hence

Applying the standard regularity theory to(3.4),we obtainThereforeu0is a desired extremal function.

Without loss of generality,we assume there exists some pointsuch that

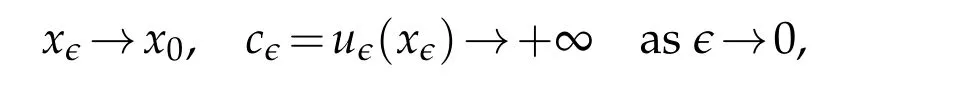
or we will replaceu∈by-u∈instead.In the sequel,we do not distinguish sequence and subsequence,the reader can understand it from the context.

4 Asymptotic behavior of extremals for subcritical functionals

In this section,we consider the asymptotic behavior of the maximizersu∈near the blowup point and away from the blow-up point. When the high order eigenvalues are involved,we can also proceed as in[40]and get similar results.

First,we shall prove thatu0=0 and obtain the following Lions type energy concentration result:

in the sense of measure,whereδx0is the usual Dirac measure centered atx0.

SupposeIn view of Lemma 2.2,we haveis bounded inLr(Ω)for any fixedrwithNote also thatis bounded inL∞(Ω).Applying the standard regularity theory to(3.4),we getu∈is uniformly bounded in Ω,which contradicts withc∈→∞as∈→0.Hence

Similar to[39,40],we can deriveWhenx0∈Ω,suppose(4.1)is not true.We can findr0＞0 and 0＜η＜1 such that

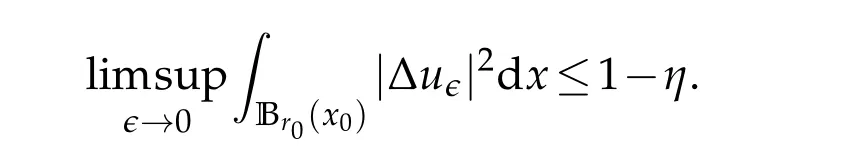
Choose a cut-off functionwhich is equal to 1 onsuch thatand

By the Adams inequality(1.5),is bounded inLr(Br0(x0))for somer＞1 and thusis bounded inLr(Br0/2(x0))provided that∈is sufficiently small.On the other hand,is bounded inL∞(Ω).Applying the standard regularity theory to(3.4),we derive thatu∈is bounded incontradictingc∈→∞.Hence we obtain(4.1).

Let

Then for any 0＜γ＜32π2,we have by the Hölder inequality and the Adams inequality(1.5),

This implies thatr∈converges to zero rapidly.To proceed,we set the following quantities

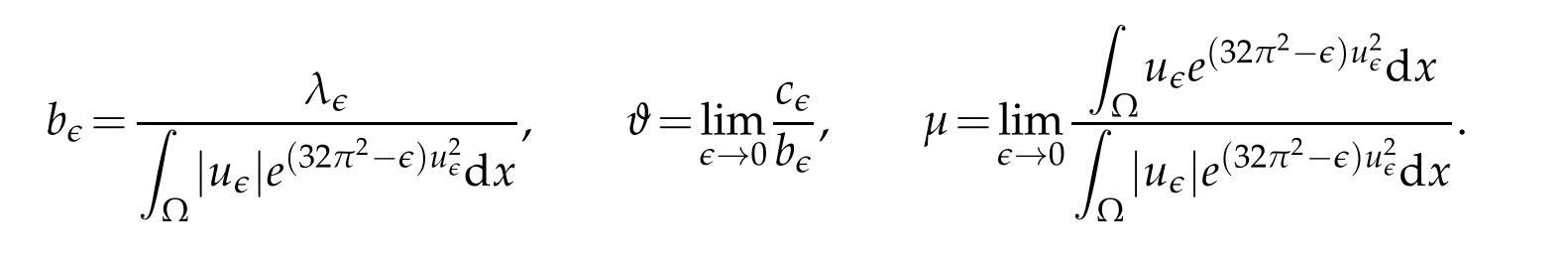
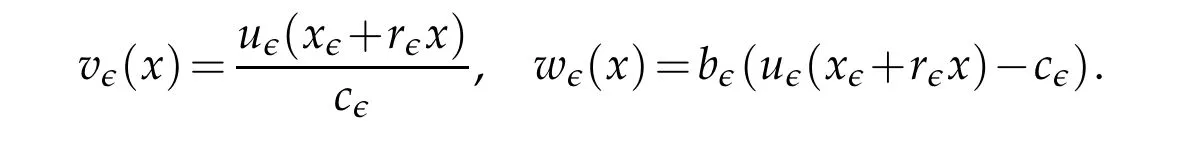
A straightforward calculation shows

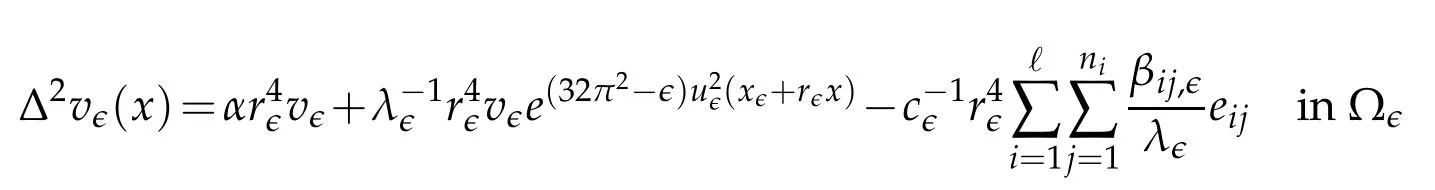
and

Obviously|v∈|≤1.Then for any fixedR＞0 andx∈BR(0),we obtain

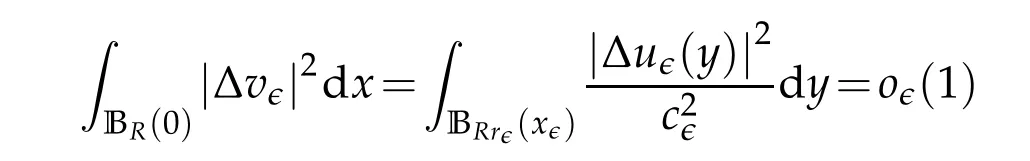
and

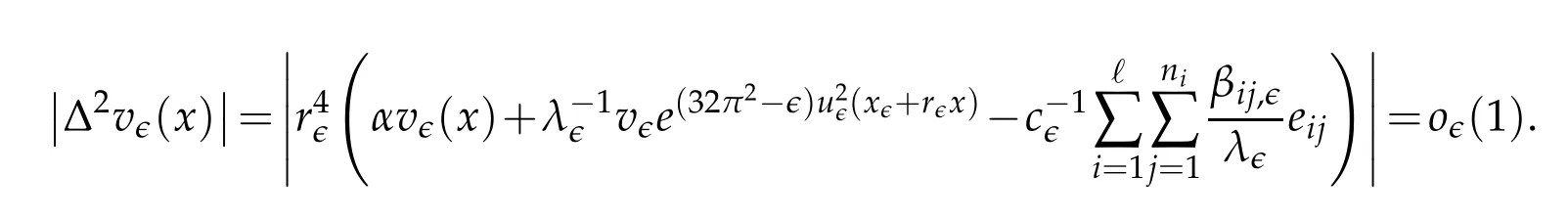
These estimates and the standard regularity theory imply

Sincewe conclude thaton R4by using the Liouville theorem.

Now we consider the convergence ofw∈. Using the Green representation formula(2.1),we get

Then form=1,2

By(2.2)and(4.2),we have for anyR＞0 andx∈BR(0)

Here we have usedb∈≤c∈and|μ|≤1.Applying the standard regularity theory to(4.3),we obtain

Ifthen we can see from(4.2),(4.4)and(4.6)thatwsatisfies

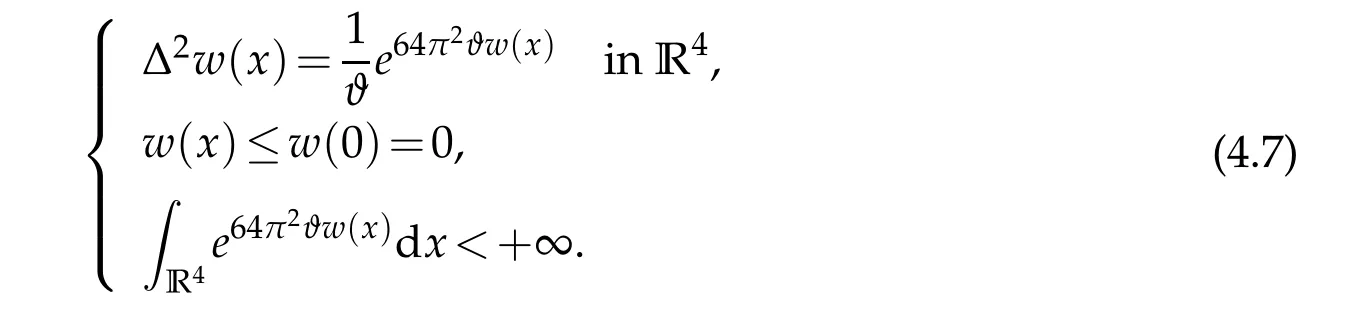
To understandw∈(x)further,we have

Hence for anyR＞0,we obtain by Fubini theorem

This together with(4.7)and the result of[45,46]implies that

Whenwe have by(4.5),.LettingR→+∞,we havew(x)is a harmonic function in R4.Sincew(x)≤w(0)=0,thenw(x)≡0 by the Liouville Theorem.

We next consider the convergence behavior ofu∈away from the blow-up pointx0.Letψ∈be a solution of the following Dirichlet problem

Using the Green representation formula(2.1),we have

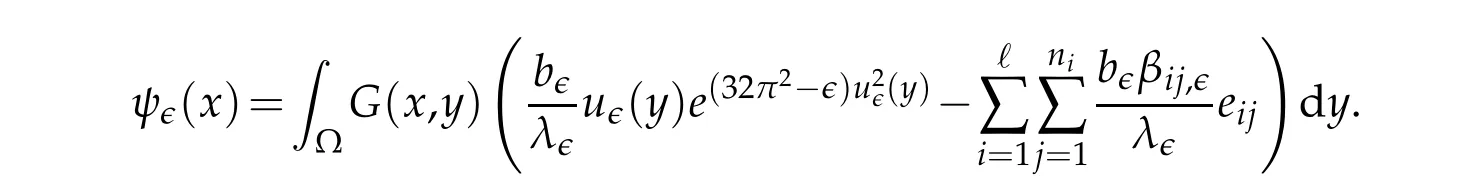
By differentiating with respect toxform=1,2,we obtain

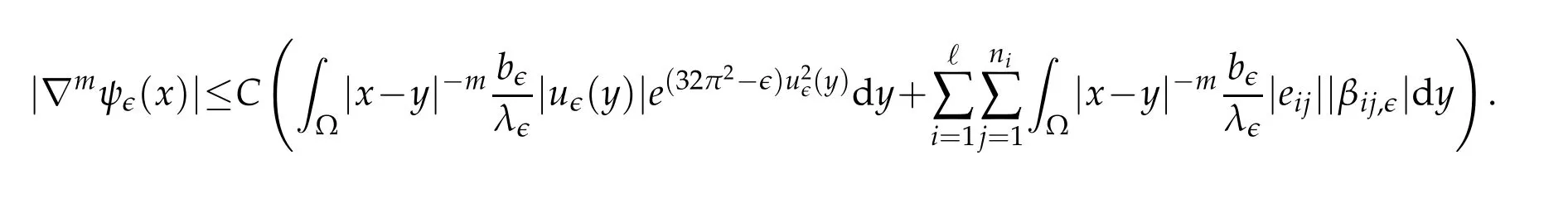
For 1＜s＜2,applying the basic inequalityfora≥0 andb≥0 and the Hölder inequality,we obtain

By the Fubini theorem,we haveform=1,2.Hence

DenoteIn view of(3.4)and(4.8),we get

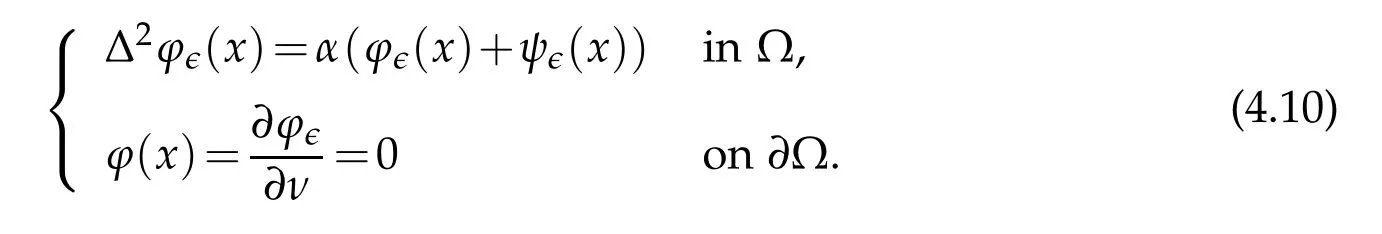
Multiplying both sides of(4.10)byφ∈,we have by the definition ofλℓ+1(Ω)and the Hölder inequality,

Then we get

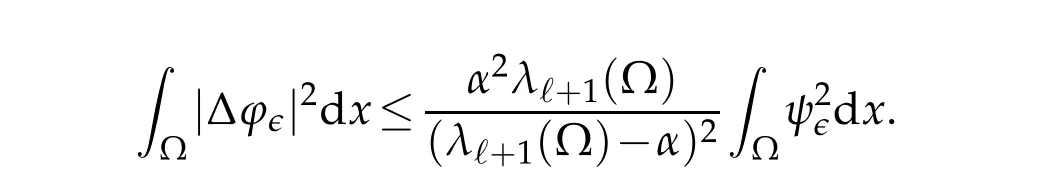
For any fixedr＞0 such that Br(x0)⊂Ω,we derive from the Adams inequality(1.5)and the cut-off function theory thatis bounded infor somep＞1.

On the other hand,is bounded inL∞(Ω).Applying the standard regularity theory we infer that

For any,we have

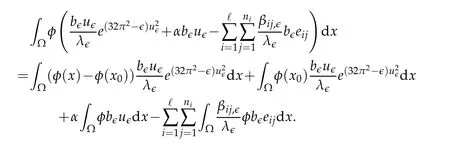
Lebesgue dominated convergence theorem implies that

Combining(3.3)and(4.12),we get

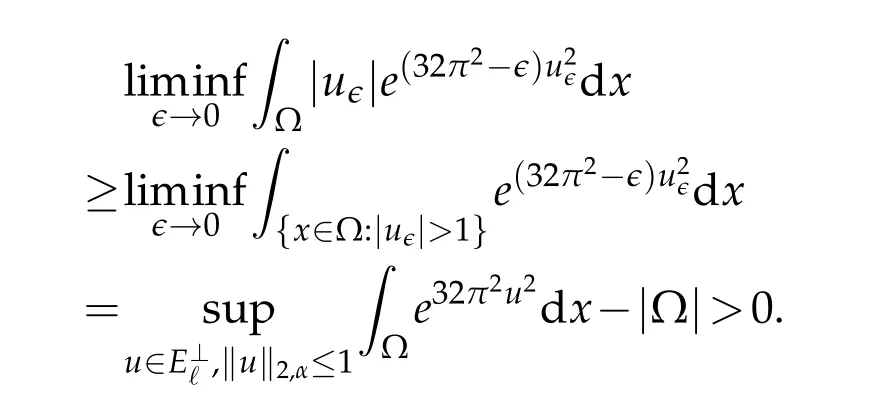
This leads to the fact thatis bounded.Using the Hölder inequality,we have

where 1/p1+1/p2=1.Here we use the factsu∈→0 strongly inLq(Ω)for anyq＞1 andis bounded infor somes＞1.By the definition ofb∈,we have

Hence

We immediately derive

On the other hand,we can easily get

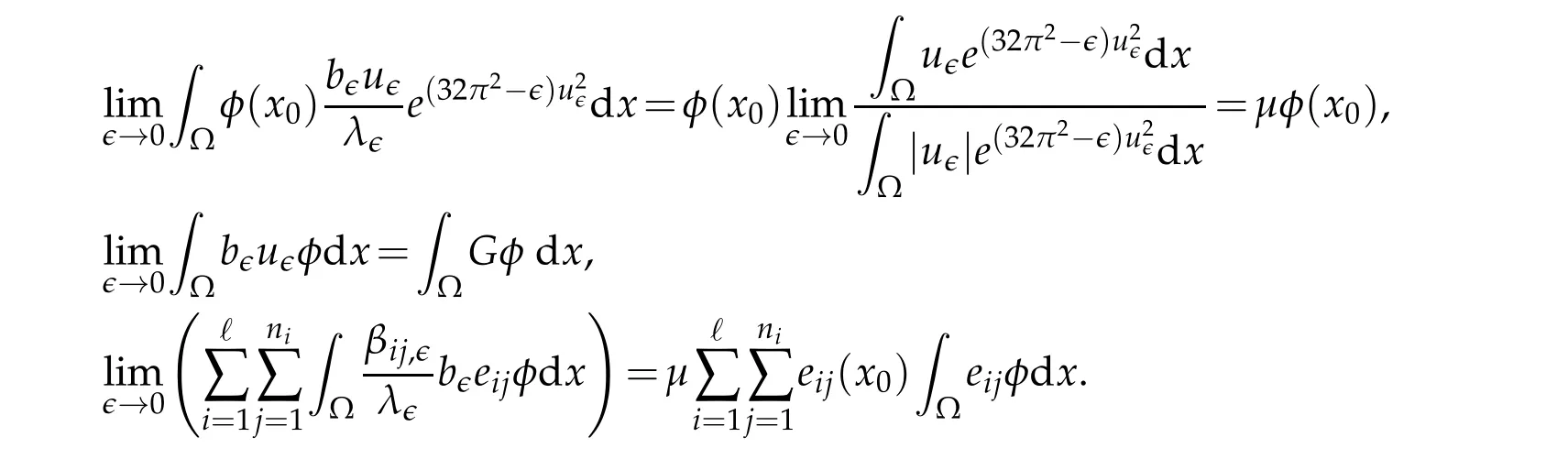
These estimates lead to

Therefore,we obtain

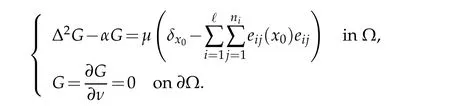
Take a cut-off functionsuch thatη≡1 onandonwhereLet

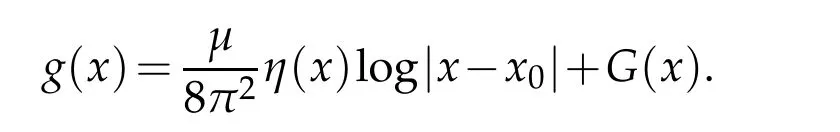
Then we have

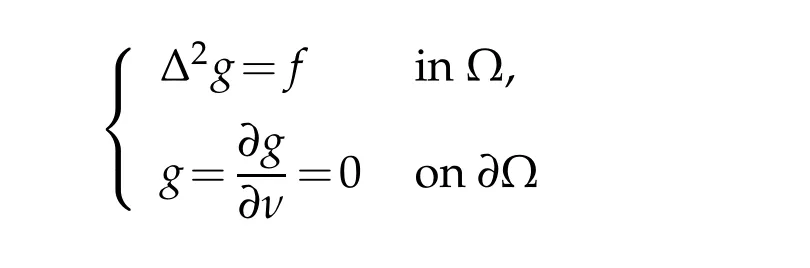
in a distributional sense,where

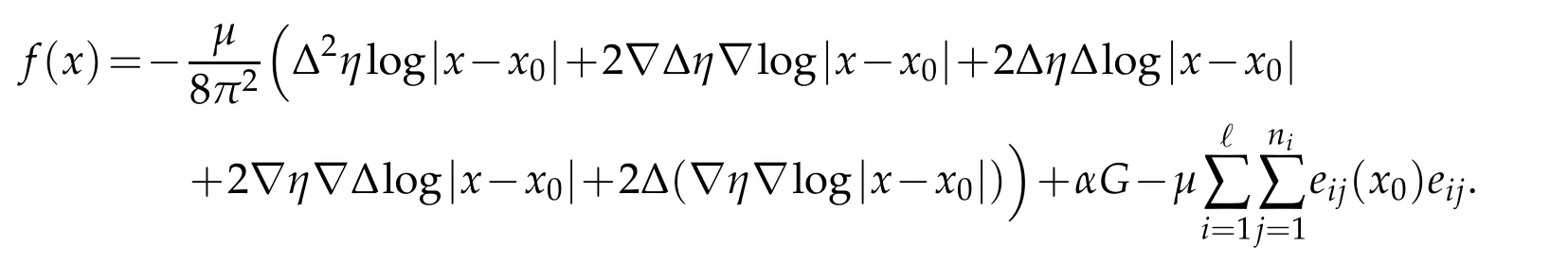
Note thatfis bounded inLt(Ω)for anyt＞1.By the standard regularity theory,we obtainSetAx0=g(x0)and

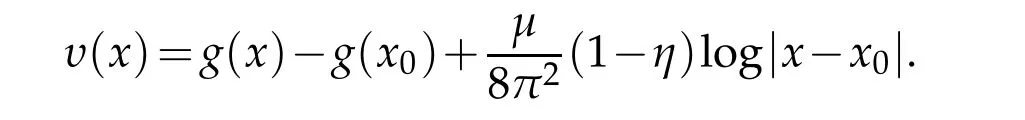
Then we get

whereis a constant depending onαandandυ(x0)=0.Sincethen

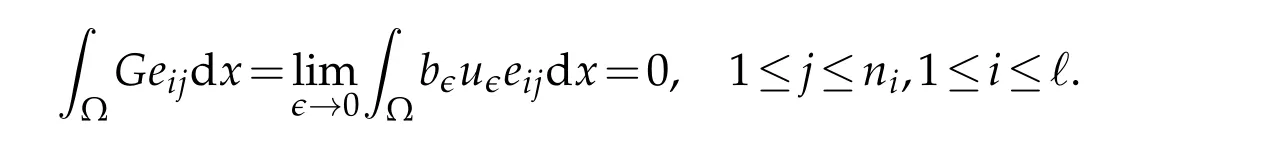
We have

5 An upper bound

In this section,we will give an upper bound of the integralThe proof is based on the Pohozaev type identity and the capacity estimates.

Set Ω′=Br(x∈),y=x∈,u=u∈and

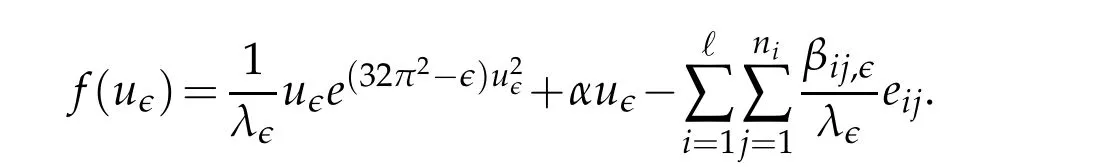
Then we have

Applying Lemma 2.1,we get for any fixedr＞0

Letting∈→0,we have

whereo∈,r(1)meansfor any fixedr＞0 andor(1)denotesBy straightforward calculation,we obtain

Therefore,we have

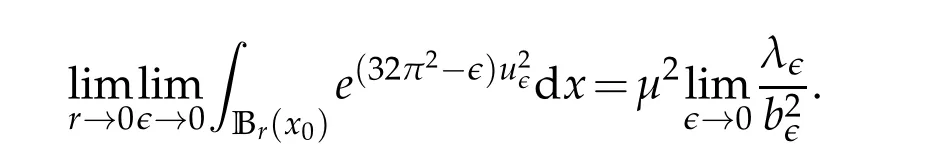
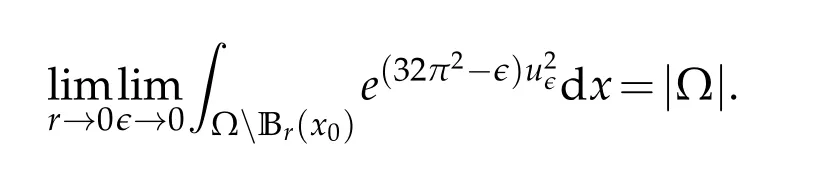
By these two identities we have

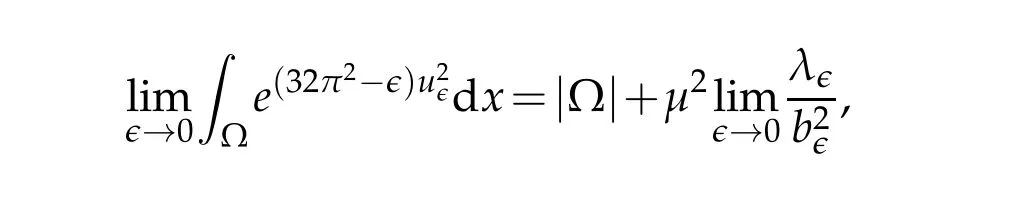
provided thatμ2＞0. Similar as that in[39,Lemma 4.6],we haveμ=1. The proof is omitted.Hence,(4.13)can be restated as

Moreover,Gcan be represented as

whereis a constant depending onx0andandυ(x0)=0.

We now point out the following results:

andis bounded.The reader can refer to[39,40]for details.In particular,b∈can be replaced byc∈in(4.11).Namely,

The technique of capacity estimates was first applied to deal with first derivatives of Moser inequality[33]. Slightly modified the proof in[40,Section 4],which is adapted from the idea of[39,Section 5],we have

Lemma 5.1.‖u‖2,α≤1,there holds

6 Test function computation

In this section,we will construct a sequence of text functionssuch thatand

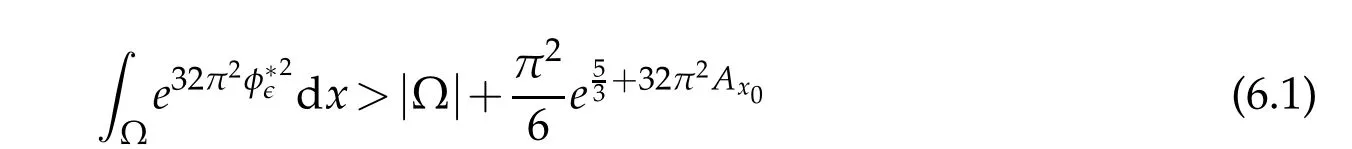
for∈＞0 sufficiently small.This leads to a contraction with(5.1).Hence,blow-up can not occur and thusc∈must be bounded.Here we must ensure that those test functions belong to the spacewhich is different from Section 7 in[40].Then the standard regularity theory leads to the existence of the desired extremal function.The proof of Theorem 1.1 is completely finished.

To prove(6.1),we writer=|x-x0|.Recall thatSet

wherea,bandcare constants of∈to be determined later,R=-log∈.In order to assure thatwe require

and

Then we have

A straightforward calculation shows

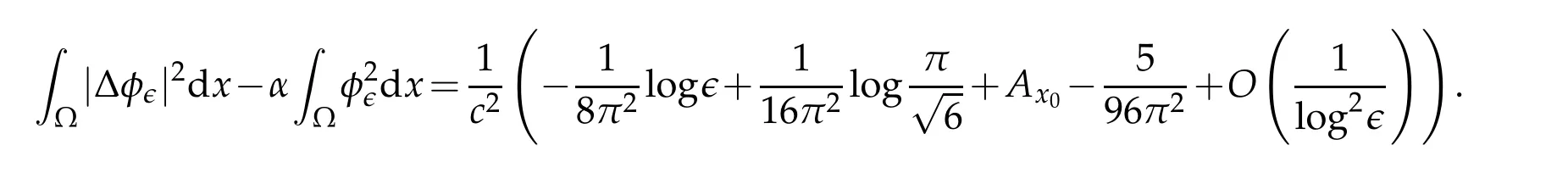
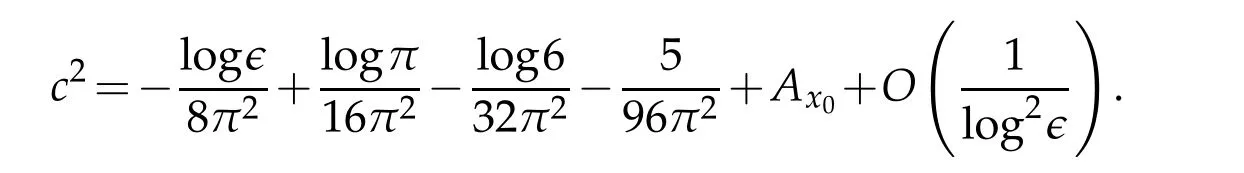
We calculate on BR∈(x0)

Hence

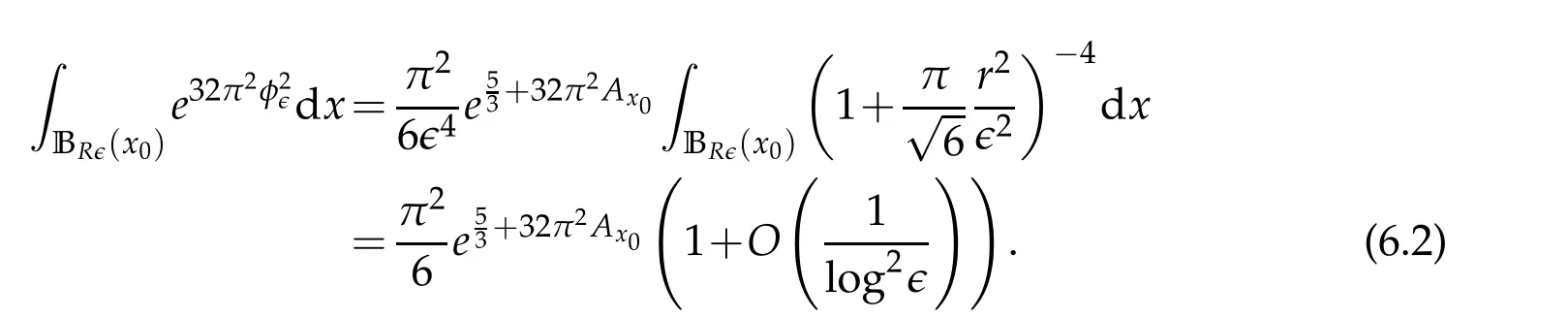
On the other hand,we get on ΩBR∈(x0)

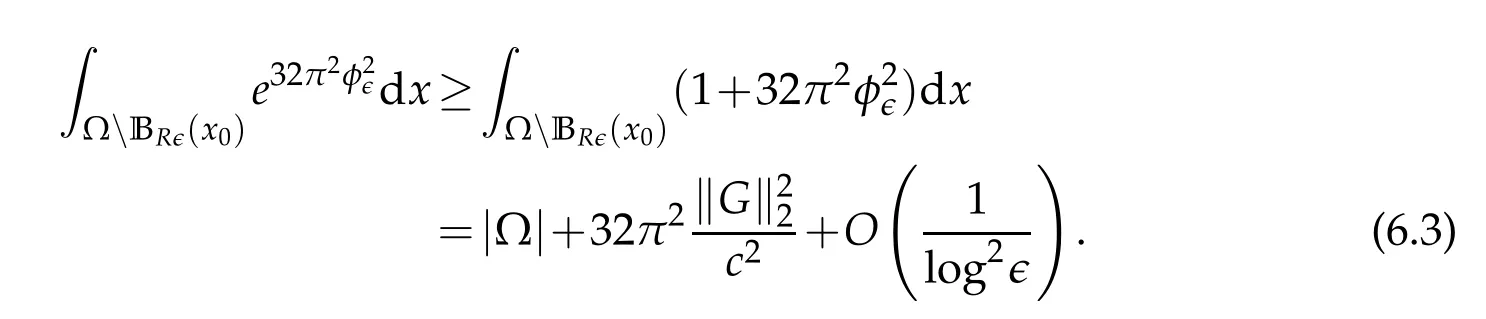
Combining(6.2)and(6.3),we conclude

where

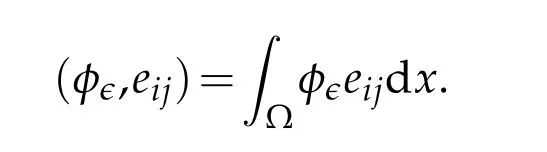
Here we have used(4.14)to obtain

Combining(6.4),(6.6)and(6.7),we derive

SetNoting thatwe getMoreoverand(6.1)holds.The contradiction between(5.1)and(6.1)shows thatc∈must be bounded.This completes the proof of Theorem 1.1.

Acknowledgement

This work was partly supported by the Outstanding Young Talents Program of the Education Department of Anhui Province(gxyq2018160).