Global Solution and Exponential Stability for a Laminated Beam with Fourier Thermal Law

RAPOSO C.,NONATO C.,VILLAGRAN O. and CHUQUIPOMA J.

1 Departamen of Mathematics,Federal University of São João del-Rei,Brazil.

2 Department of Mathematics,Federal University of Bahia,Brazil.

3 Department of Mathematics,Universidad del Bío-Bío,Chile.

Abstract.This paper focuses on the long-time dynamics of a thermoelastic laminated beam modeled from the well-established Timoshenko theory.From mathematical point of view,the study system consists of three hyperbolic motion equations coupled with the parabolic equation governed by Fouriers law of heat conduction and,in consequence,does not belong to one of the classical categories of PDE.We have proved the well-posedness and exponential stability of the system.The well-posedness is given by Hille-Yosida theorem.For the exponential decay we applied the energy method by introducing a Lyapunov functional.

Key Words:Global solution;laminated beam;Timoshenko;thermoelasticity;energy method.

1 Introduction

The one dimensional thermoelastic system is given by

In this model,ρdenotes the mass density,athe elasticity coefficient,a the stresstemperature andcthe heat conductivity.The functionsuandθare the displacement of the solid elastic material and the temperature difference.For existence and the asymptotic stability of the solutions we cite the pioneer work of Dafermos[1]where it is proven that the temperature gradient and the specific entropy always converges to zero.

As a rule,the displacement also decays to zero as time goes to infinity.Several efforts have shown asymptotic stability,specifically[2,3]and reference therein.In these studies,the authors proved that the total thermoelastic energy decays to zero exponentially as time goes to infinity for material subject to Dirichlets,Neumanns and also mixed boundary conditions.The beam deflection when subjected to transverse displacementuand rotation angleψis mathematically described by the system developed by Timoshenko[4],which is given by two coupled differential equations

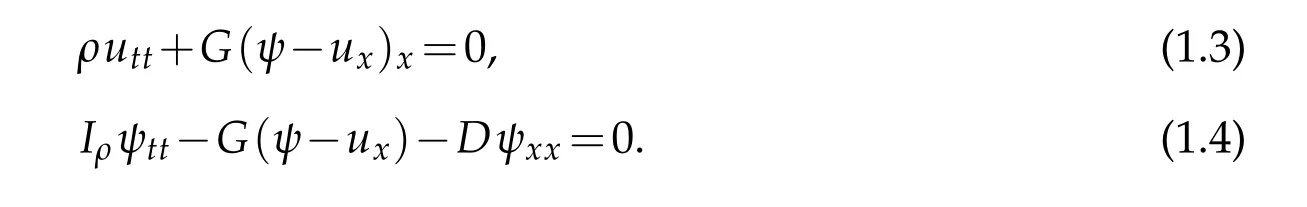
The coefficientsρ,IρandGare the mass per unit length,the polar moment of inertia of a cross section and the shear modulus,respectively.D=EIwhereEis Youngs modulus of elasticity andIis the moment of inertia of a cross section.

The model for two identical Timoshenko beams,taking into account that an adhesive of the small thickness is bonding the two layers producing the structural damping due to the interfacial slip,was proposed by Hansen and Spies[5,6]and is given by

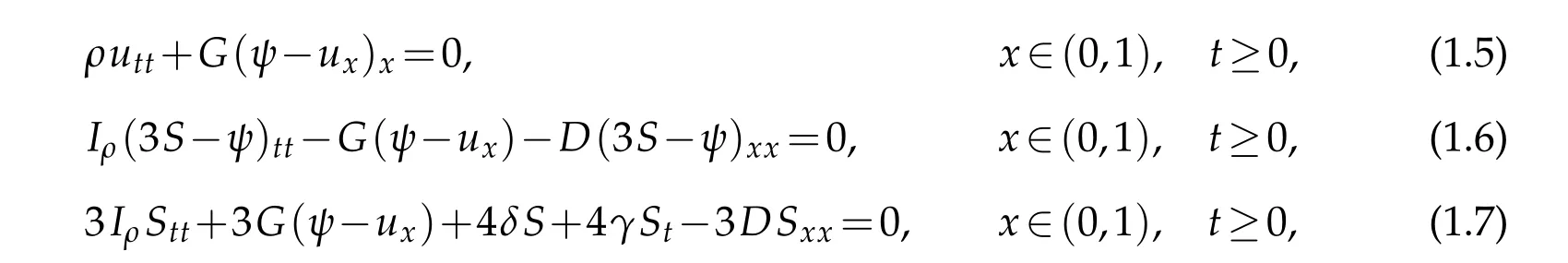
whereu(x,t)represents the transverse displacement,ψ(x,t)is the rotation angle displacement andS(x,t)is proportional to the amount of slip along the interface.The system(1.5)-(1.7)describes the dynamics of transverse displacement,rotation angle and interfacial slip,respectively.The coefficientsδandγare the adhesive stiffness and adhesive damping of the beams.

Regarding the stabilization of the system(1.5)-(1.7),we mention[7–10]and references therein.In[9],it is proven that the structural damping 4γStcreated by the interfacial slip alone is not enough to stabilize the system(1.5)-(1.7)exponentially to its equilibrium state.Reference[10]showed that when the frictional damping is present in all components,

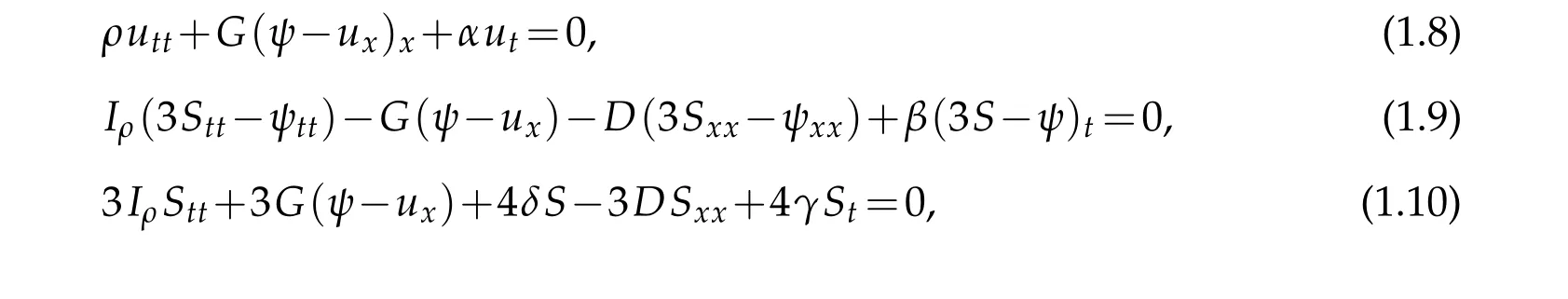
the full damped laminated beam(1.8)-(1.10)is exponentially stable without any condition on the coefficients of the system.

Authors in reference[11]considered a laminated beam with a single control in form of frictional damping in the second equation,

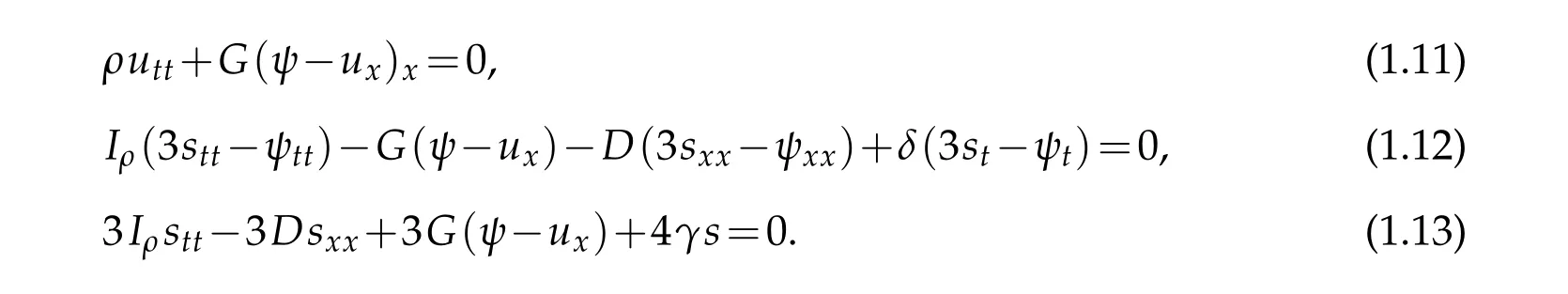
Authors improved the result obtained in[10]and proved that a unique dissipation through the frictional damping is strong enough to exponentially stabilize the model without any condition on the coefficients of the system. A good reference to wave equations with frictional damping is given in[12].

Dynamics of Laminated Timoshenko beams was studied in[13]where authors established the existence of smooth finite dimensional global attractors for the corresponding solution semigroup. Hybrid laminated Timoshenko beam model was considered in[14]where the beam is fastened securely on the left while on the right it is free and has an attached container.Using the semigroup approach and a result of Borichev and Tomilov,[15],the authors proved that the solution is polynomially stable.

The system(1.5)-(1.7)is closely related with Timoshenko theory.In[16]the exponential stability for Timoshenko system(1.3)-(1.4)with a frictional damping in each component was proven.There is extensive bibliography for thermoelastic Timoshenkos system.For instance,we cite[17]and references therein.

For analysis aspects we mention the work[18],where the property of growth determined by spectrum of operator associated with the Timoshenko system with weakly dissipation was given. This kind of approach is relevant because analytic semigroups have the spectrum determined growth property.This property presents the type of semigroup and also indicates that the best constant for the exponential stability is the upper bound of the spectrum of operator.

In[19],authors considered a thermoelastic laminated beam with structural damping,coupled to a heat equation modeling an expectedly dissipative effect through heat conduction given by Gurtin-Pipkin thermal law.Authors established the well-posedness for the problem.Furthermore,under some assumptions on the relaxation function,they proved the exponential stability and lack of exponential stability for the problem.

The main difficulty carried out in this paper is the presence of the Fourier law of heat conduction that can produce lack of exponential stability when the wave speed is different for systems partially damped(see[20]).Recent studies have lead to the existence of a second spectrum is an essential element to justify,from the physical point of view,the imposed condition of equal wave speed.For more information on this subject,we cite[21]and reference therein.

For example,in[22]the author took into account that only dissipation in the system is through heat conduction in the interfacial slip equation given by Fouriers law.In his manuscript was proved that this unique dissipation is strong enough to exponentially stabilize the system provided the wave speeds of the system are equals.

To overcome this technical difficulty,we consider in this paper a damping in each dynamic equation of the system and focus our attention to a full damped laminated Timoshenko thermoelastic system.More precisely,we deal with the system below,where the dissipative action of the temperature on the transverse displacement generates a coupling term given by the stress tensorutx,

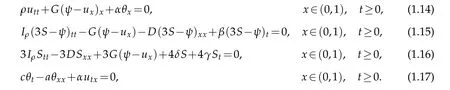
We assume that the beam is firmly clamped and thermally insulated at the end of both sides.We consider the mixed boundary conditions

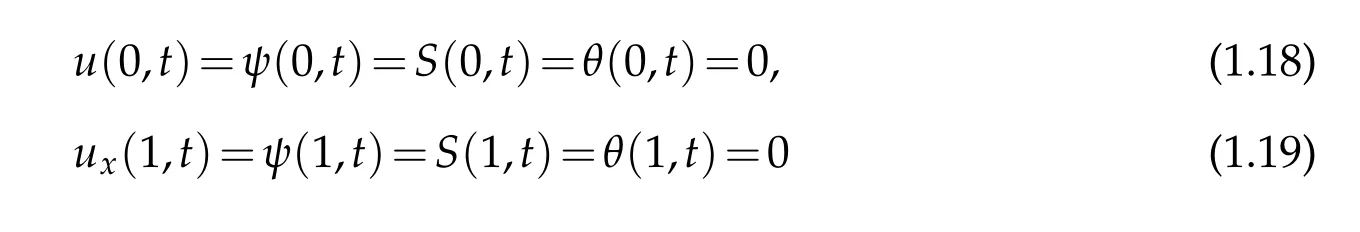
and initial data

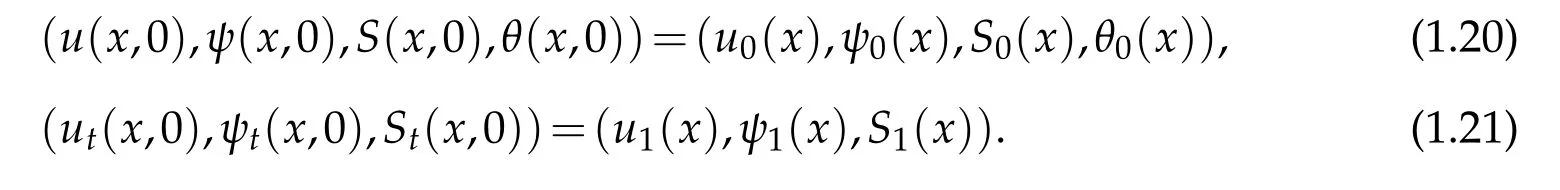
We use Sobolev spaces with its proprieties as in[23]. We shall focus here on the asymptotic behaviour of the system(1.14)-(1.17).This paper has the following sections.In Section 2 by semigroup approach we present the phase space.In Section 3 we prove the well-posedness.In the last section,we deal with the asymptotic behavior.We calculate the full energy of the system and prove its dissipative property.We present some technical lemmas and by the energy method,that consists in the use of suitable multiplies to build a functional of Lyapunov for the system,we prove the exponential stability of solution.

2 The semigroup setup

Let

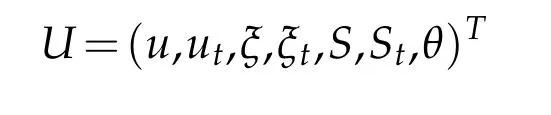
be a vector function,whereThe system(1.14)-(1.17)can be written as follows

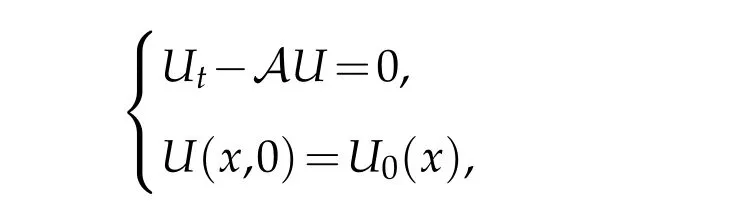
with phase space

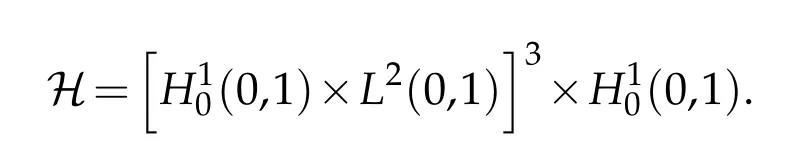
For the standardL2(0,1)space,the scalar product and the norm are denoted by

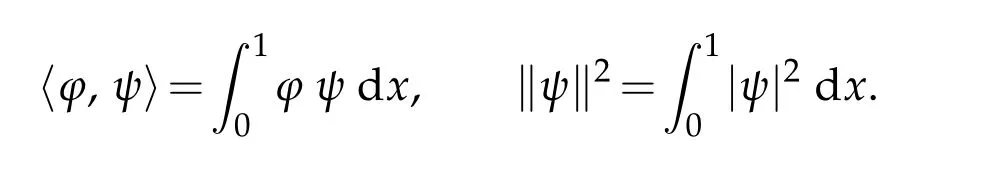
H is a Hilbert space with the following inner product

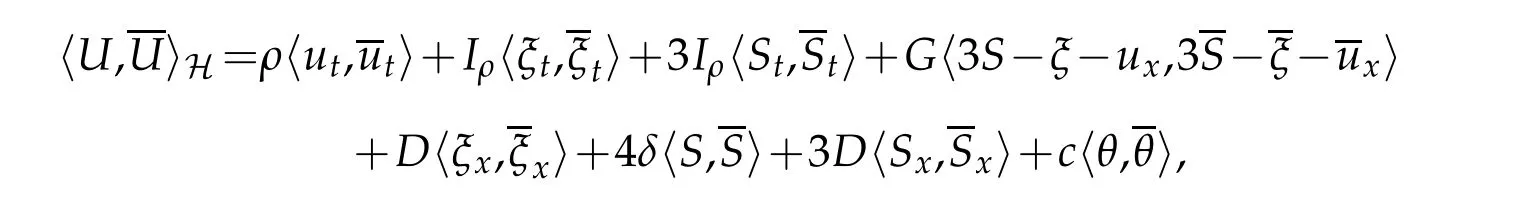
where

The domain of A is given by

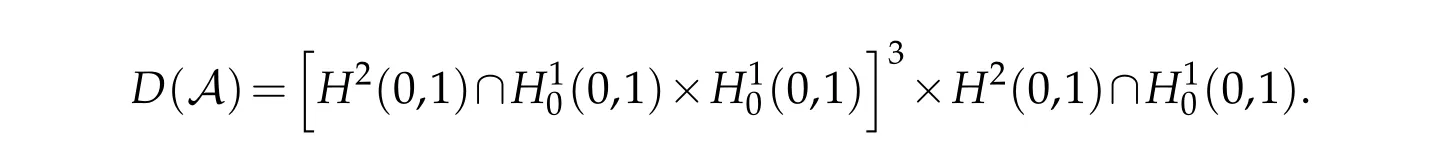
3 The well-posedness

To prove the well-posedness,we use the Hille-Yosida theorem.

Lemma 3.1.The operatorAis dissipative.

Proof.

Integrating by parts and using mixed boundary conditions(1.18)-(1.19),we obtain

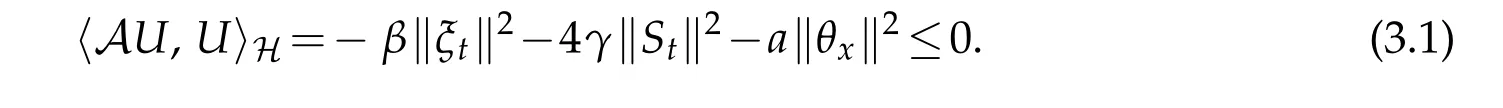
This completes the proof of the lemma.

Lemma 3.2.The operator I-Ais surjective.

Proof.For anyf=(f1,f2,···,f7)∈H andthe equation(I-A)U=fleads to

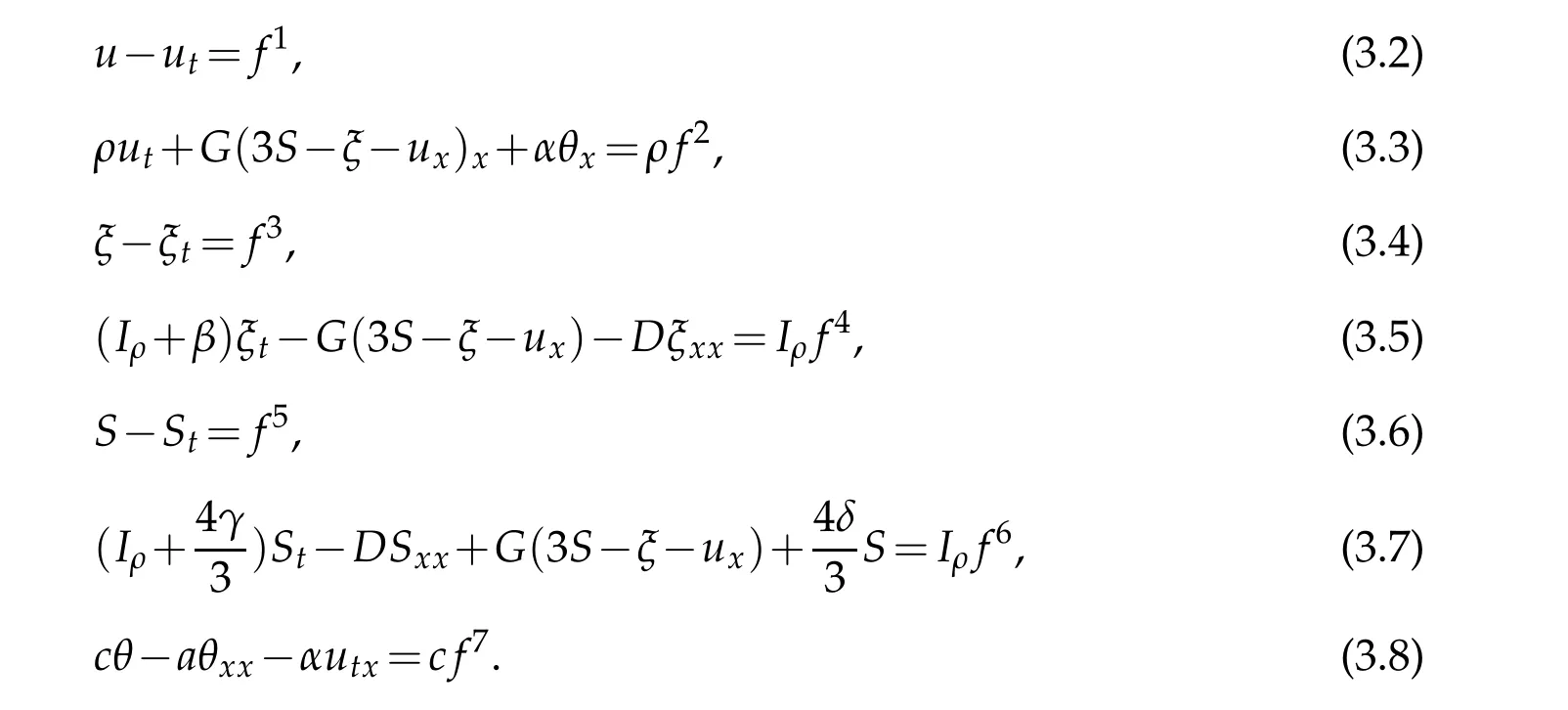
Replacing(3.2),(3.4),(3.6)into(3.3),(3.5),(3.7),respectively,we obtain

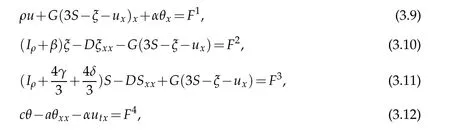
where

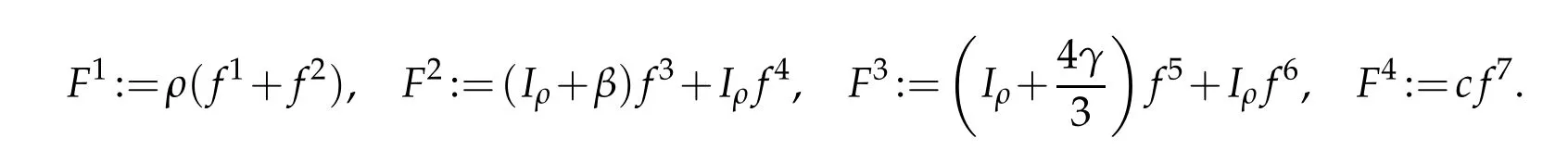
Multiplying(3.9)–(3.12)byv1,v2,v3,v4respectively and integrating by parts,we obtain

for allDenoting

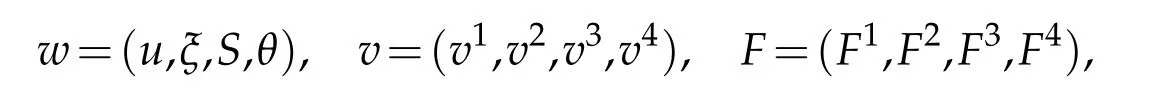
we introduce the Hilbert spaceequipped with the norm

We arrive the following variational formulation

where

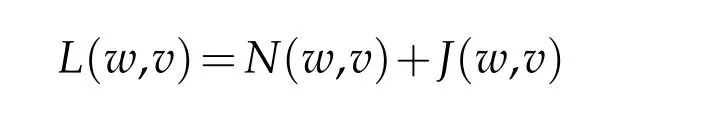
with

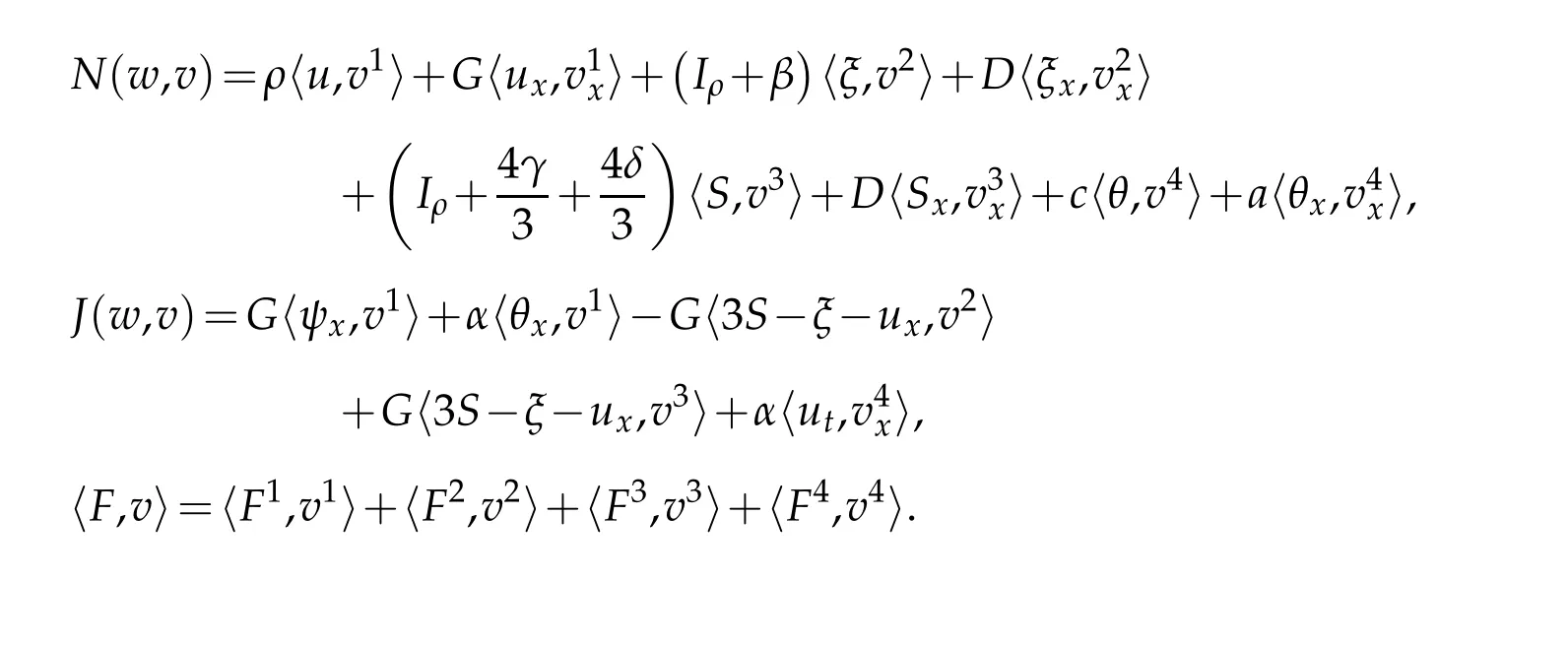
It is clear thatL(w,v)is bounded.Note thatfurthermore,from equivalence betweenN(w,w)andJ(w,w),we can obtain a positive constant∈such that

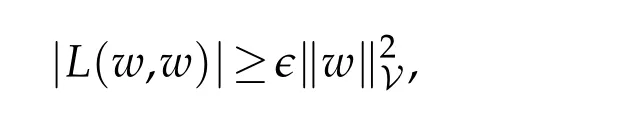
which implies thatL(w,v)is V-elliptic. Hence,we have thatL(w,v)is a bilinear,continuous and V-elliptic form on V×V. Applying the Lax-Milgram Theorem,(see[24],Theorem 3.1.4 page 115)we assert that for allF=(F1,F2,F3,F4)∈V there exists a unique solutionsuch that(3.13)holds.Consequently,the substitution ofjust obtained into(3.2),(3.4),(3.6)yieldsFrom(3.9)-(3.12),we have

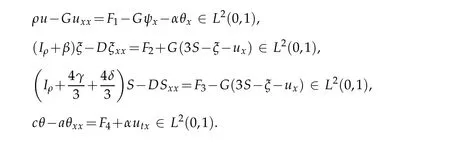
Thus,by the regularity theory for the linear elliptic equations,we have that2(0,1)and thenSoHence,the operatorI-A is surjective.

The well-posedness is given by the following theorem.

Theorem 3.1.Let U0∈H,then the system

has a unique weak solution

Moreover,if U0∈D(A)then

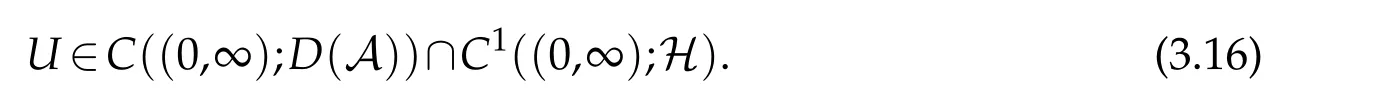
Proof.ClearlyD(A)is dense in H.As A is dissipative andI-A is surjective,then by Hille-Yosida Theorem(see Theorem 1.2.2,page 3,[25])we have thatAgenerates aC0-semigroup of contractions S(t)on H. It follows from semigroup theory thatU(t)=S(t)U0is a unique solution of(3.14)satisfying(3.15)and(3.16).

4 Asymptotic behavior

4.1 Energy of the system

In this section we deduce the full energy of the system(1.14)-(1.17)and will prove that the energy is non-increasing and uniformly bounded above byE(0).In fact we have the following result.

Theorem 4.1.The energy of the system is given by

and satisfies

Proof.Multiplying(1.14)byut,(1.15)by(1.16)byStand(1.17)byθrespectively,we obtain

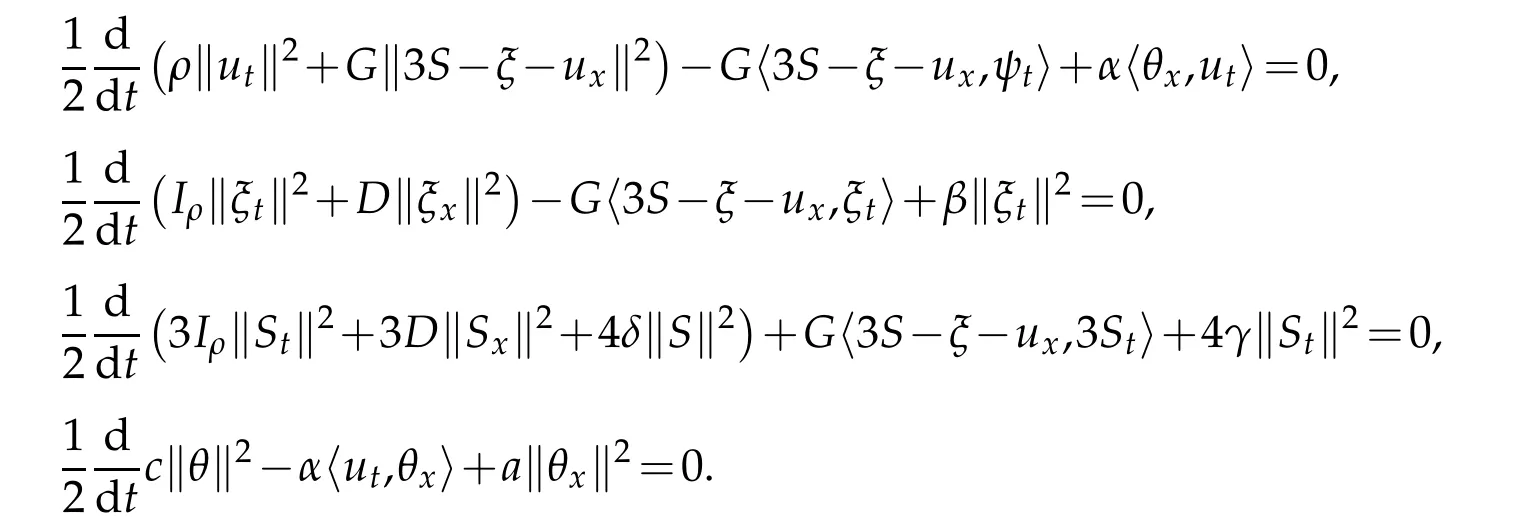
Adding these four equations our conclusion holds.

4.2 Technical lemmas

In the previous section we observe that the energy functional restores some energy terms with a negative sign.We are interested in building a Lyapunov functional that restores the full energy of the system with negative sign,and for this goal,we consider the following lemmas.

Lemma 4.1.Defining

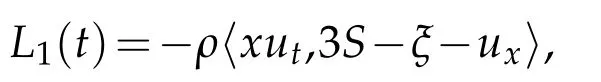
we have

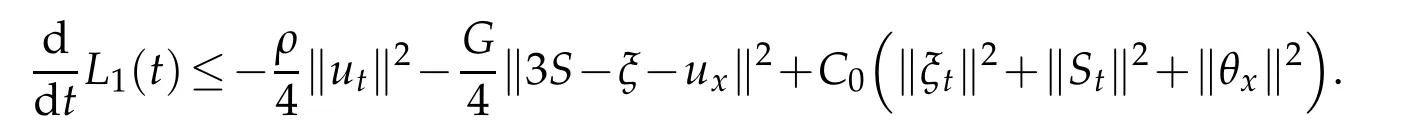
Proof.We have that

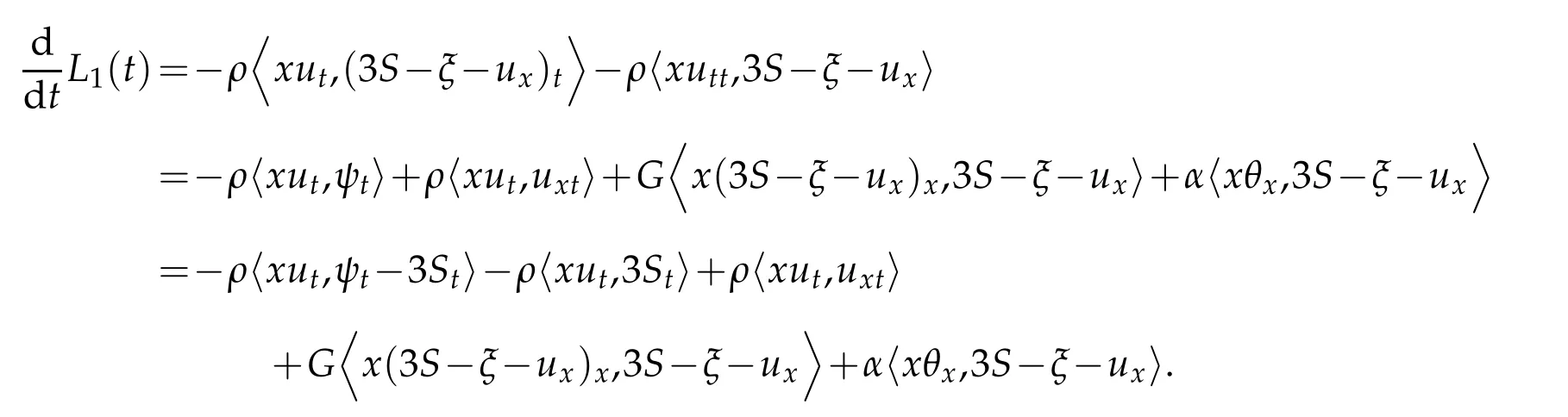
Integrating by parts and applying the mixed boundary conditions we have

From Young’s inequality we obtain

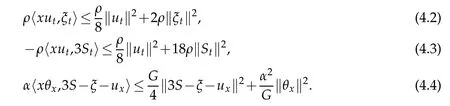
Plugging(4.2)–(4.4)with(4.1)and denotingwe conclude the prove of lemma.

Lemma 4.2.Introducing the functional

we get

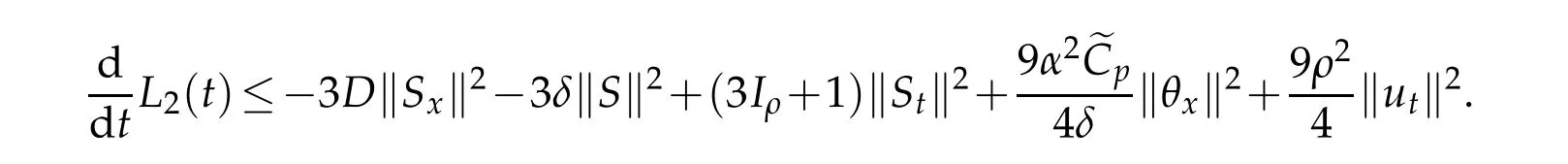
Proof.By derivative of〈St,S〉we obtain

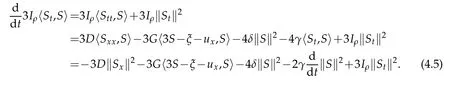
Note that

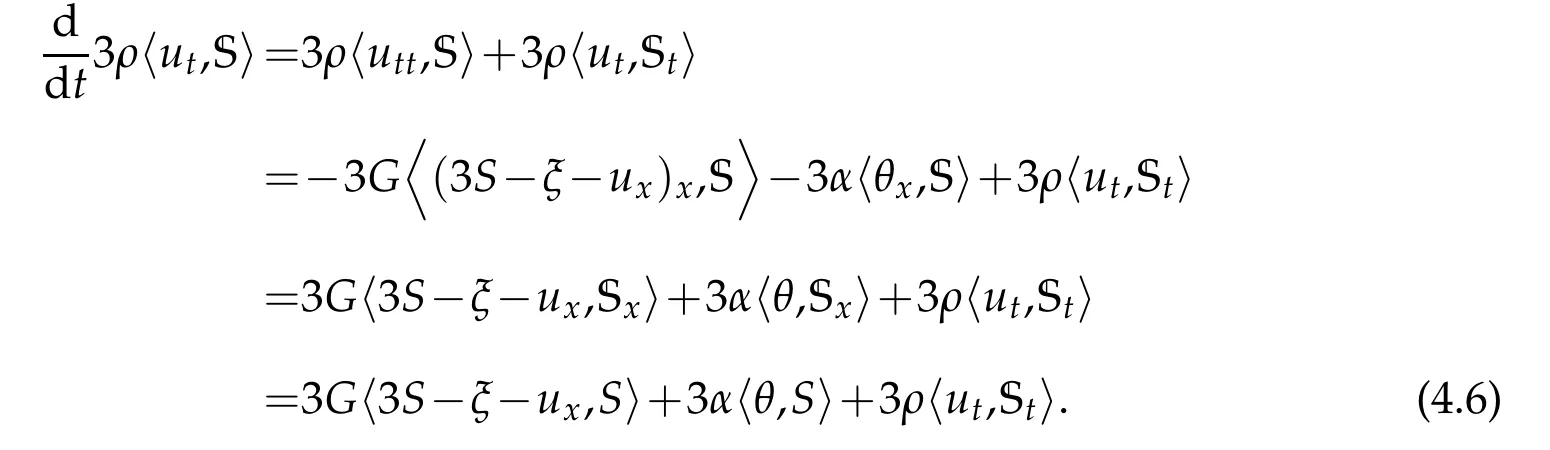
From Young’s and Poincaré’s inequalities and usingwe obtain from(4.6)that

Now let us recover the last term of the full energy,with negative signal,that is necessary to build the Lyapunov functional.In this direction,we present the last technical lemma.

Lemma 4.3.The functionalΦ(x,t)defined by

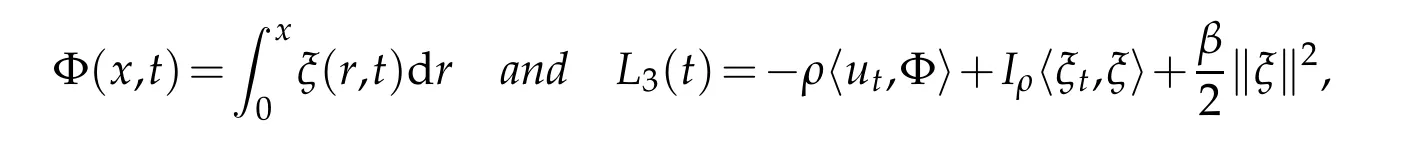
has the following property

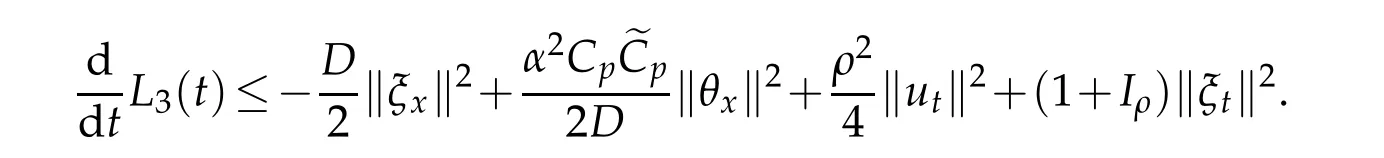
Proof.The derivative ofsatisfies

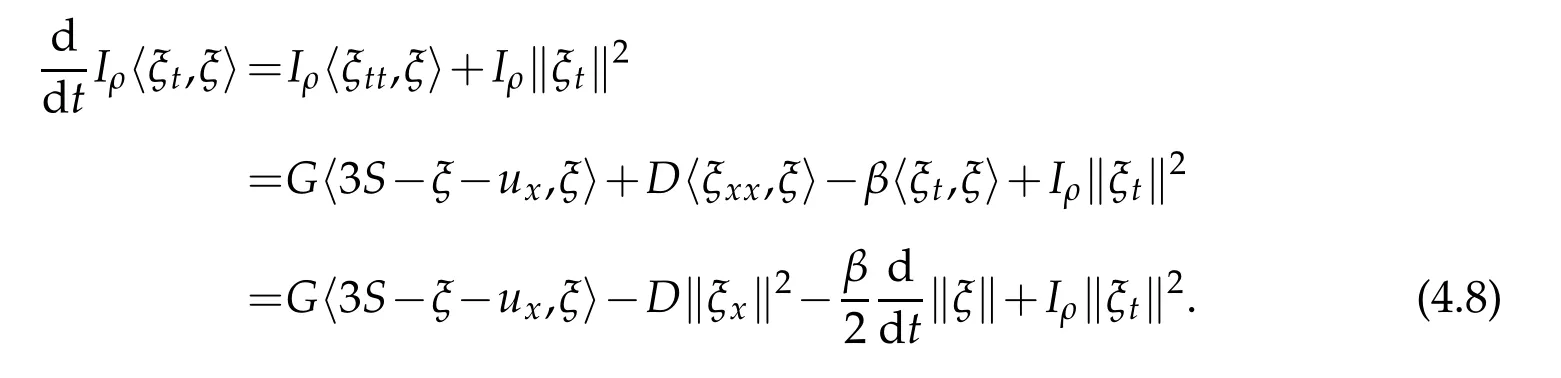
Similarly as in the previous lemmas,we deduce that

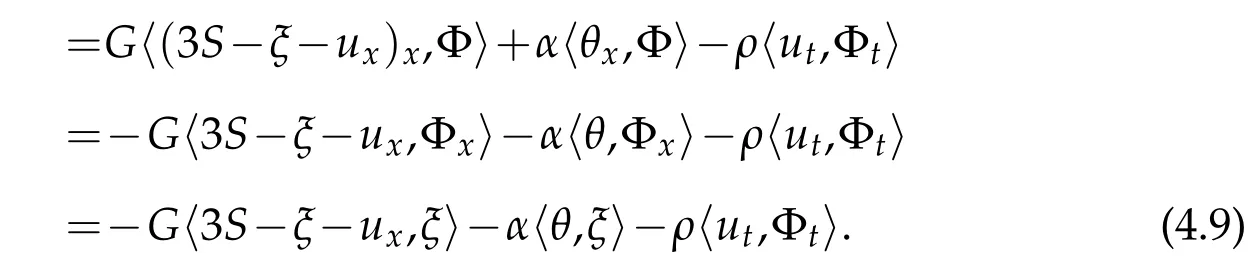
From Young’s and Poincaré’s inequalities and usingwe obtain from(4.9)that

whereCpis the Poincaré’s constant.Adding(4.8)and(4.10)we conclude the lemma.

4.3 Exponential decay

Now we are in position to prove our principal result.

Theorem 4.2.The problem(1.14)-(1.17)is exponentially stable,that is,

Proof.We will to construct a suitable Lyapunov functional L satisfying the following equivalence relation

for somec1,c2＞0 and the proof that

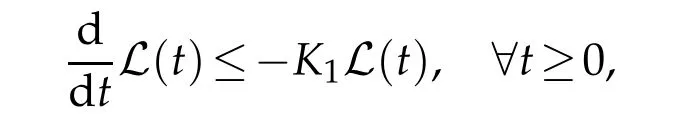
which implies that

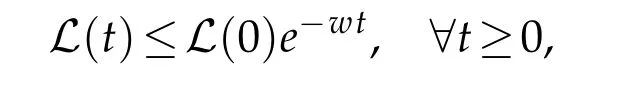
for somew＞0.

From previous lemmas,we have

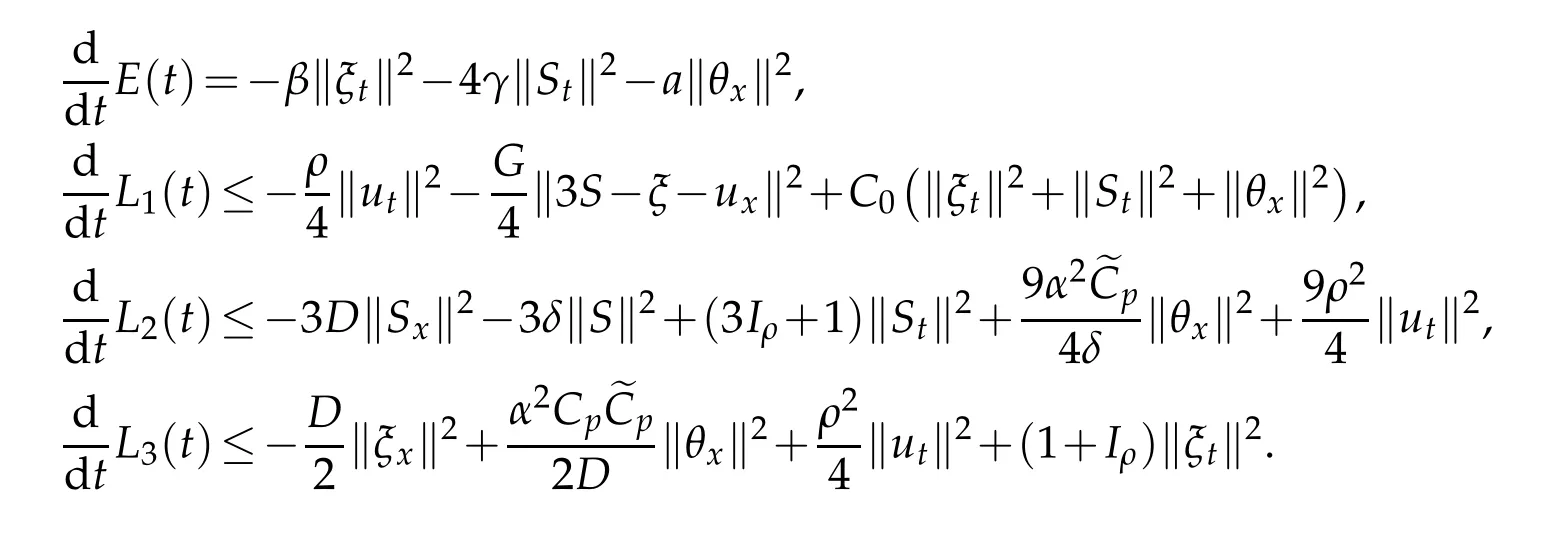
Now we define the Lyapunov functional L(t)by

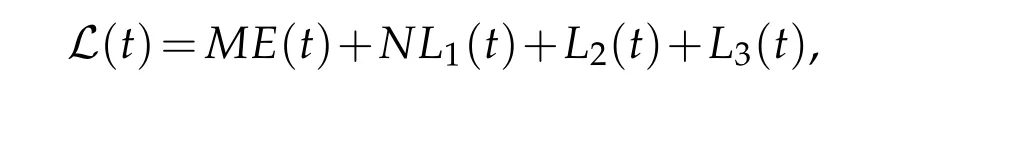
then

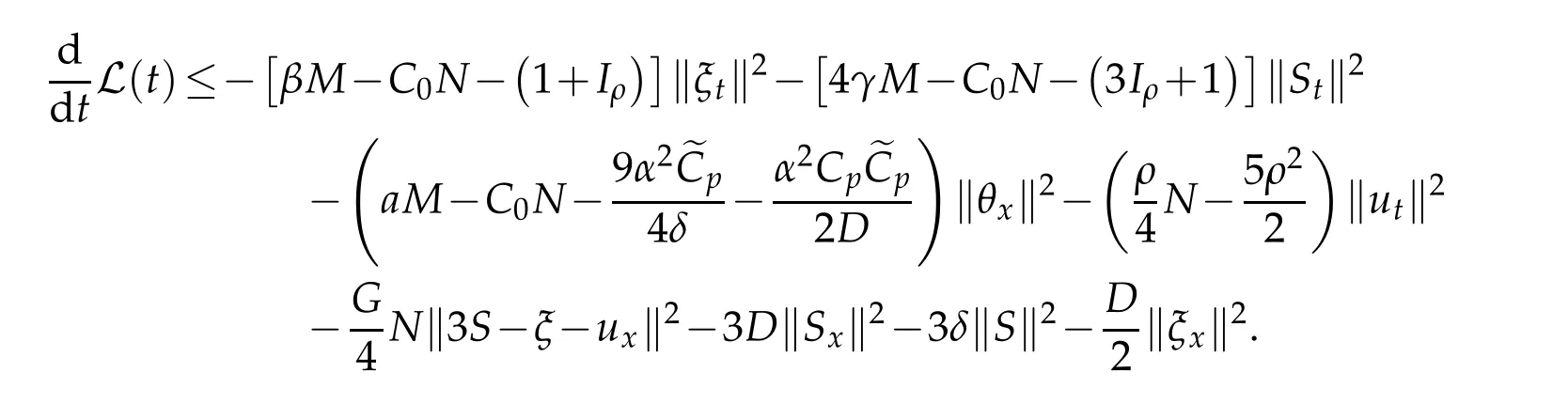
ChoosingM,Nlarge enough withM＞Nand applying Poincaré’s inequality,we obtain

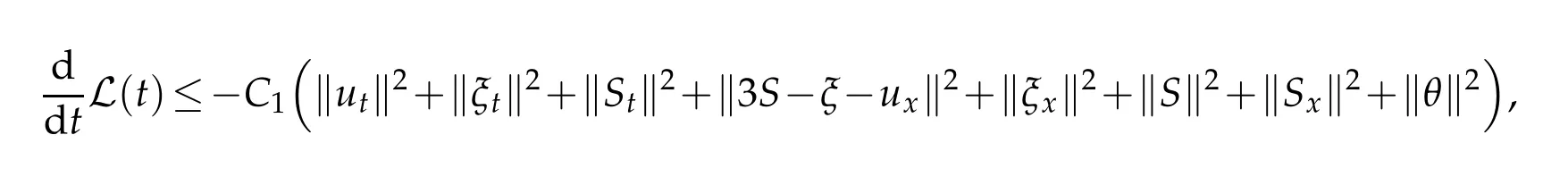
for someC1＞0.Using energy functional and(4.11),we end up with

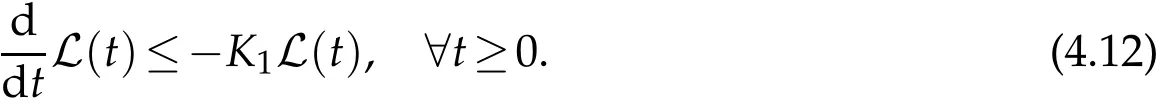
A simple integration of(4.12)over(0,t)yields

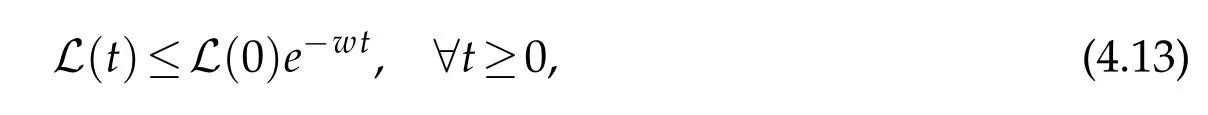
for somew＞0.From inequality(4.13)implies the exponential decay of L(t)and consequently by equivalence(4.11),the exponential decay ofE(t),then we conclude that

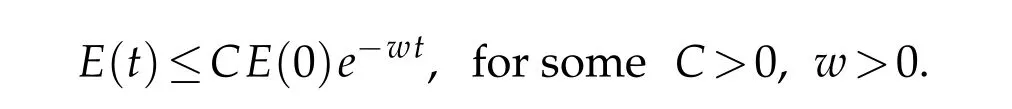
This completes the proof of the theorem.

Acknowledgments

C.Nonato was partially supported by CAPES(Brasil)and O.Villagran was partially supported by project FONDECYT/1191137.The authors would like to thank the anonymous referees for his careful reading of our work and suggestions that improved this manuscript. Also,the authors would like to express their gratitude to Professor Huy Hoang Nguyen for the fruitful discussions concerning this paper.