On a Quasilinear Degenerate Parabolic Equation from Prandtl Boundary Layer Theory

OUYANG Miao

1 School of Applied Mathematics,Xiamen University of Technology,Xiamen 361024,China.

2 Department of Mathematics,Southwest Jiaotong University,Chengdu 610000,

China.

Abstract.The equation arising from Prandtl boundary layer theoryis considered. The existence of the entropy solution can be proved by BV estimate method. The interesting problem is that,since a(·,x,t)may be degenerate on the boundary,the usual boundary value condition may be overdetermined.Accordingly,only dependent on a partial boundary value condition,the stability of solutions can be expected.This expectation is turned to reality by Kružkov’s bi-variables method,a reasonable partial boundary value condition matching up with the equation is found first time.Moreover,if the stability can be proved even without any boundary value condition.

Key Words:Prandtl boundary layer theory;entropy solution;Kružkov’s bi-variables method;partial boundary value condition;stability.

1 Introduction

The initial-boundary value problem of the quasilinear degenerate parabolic equation

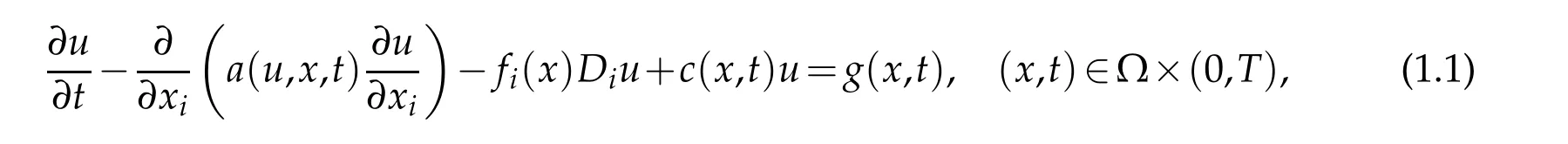
is considered in this paper,whereis a appropriately smooth open domain,the double indices ofirepresent the summation from 1 toNas usual.

Equation(1.1)arises from the boundary layer theory[1]etc.As the simplification of the Navier-Stokes equation,the Prandtl boundary layer equation describes the motion of a fluid with small viscosity about a solid body in a thin layer which is formed near its surface owing to the adhesion of the viscous fluid to the solid surface.In particular,we consider the motion of a fluid occupying a two dimensional region is characterized by the velocity vectorV=(u,v),whereu,vare the projections ofVonto the coordinate axesx,y,respectively,assume that the density of the fluidρis equal to 1,then the Prandtl boundary layer equation for a non-stationary boundary layer arising in an axially symmetric incompressible flow past a solid body has the form[1]

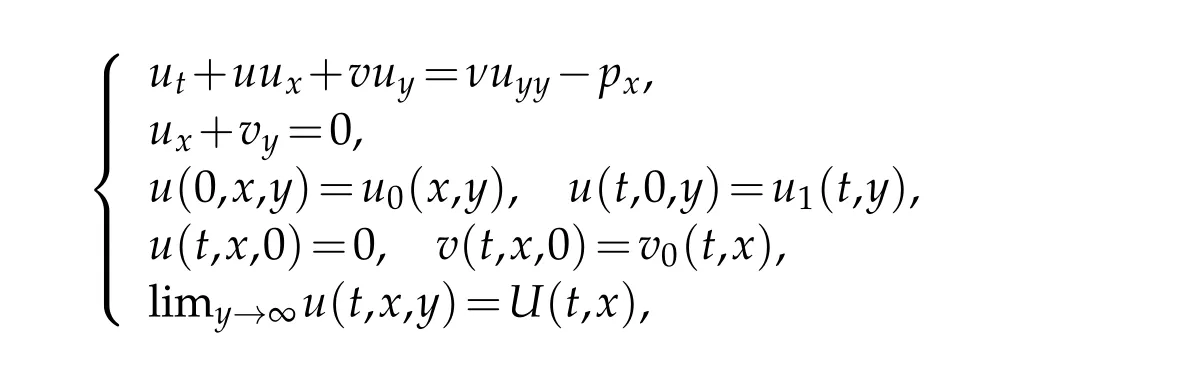
in a domainD={0＜t＜T,0＜x＜X,0＜y＜∞},whereν=const＞0 is the viscosity coefficient of the incompressible fluid,u0＞0,u1＞0 fory＞0,u0y＞0,u1y＞0 fory≥0,where,p=p(t,x)is the pressure,U=U(t,x)is the velocity at the outer edge of the boundary layer which satisfies

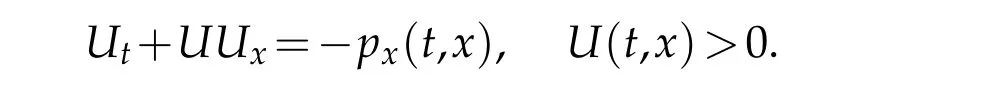
By the well-known Crocco transform,

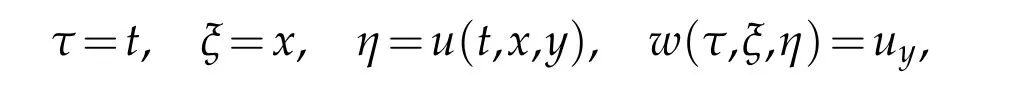
we can show thatuy=wsatisfies the following nonlinear equation

By a linearized method,Oleinik had shown that there is a local classical solution to this equation[2].Although there are some important papers to studied the global solutions of the Prandtl boundary layer equation[3-8],the related problems are far from being solved. For example,the compatibility problem between Navier-Stokes equation and Prandtl boundary layer equation.For another example,whether there is a global solution of equation(1.4)and whether this global solution can be deduced a global weak solution of the Prandtl boundary layer equation by the inverse transform of Crocco transform?In fact,if the domain is not theN-dimmensional cube,whether the inverse transform of Crocco transform exists or not is still unsolved.In addition,many reaction-diffusion problems can be summed up to equation(1.1)[2].

In this paper,we will consider the global solutions of equation(1.1).After the pioneering work[3]by Vol′pert-Hudjaev,the Cauchy problem of equation(1.1)had been studied in[10-19]etc.,the solutions to the Cauchy problem of equation(1.1)are wellposedness.Also,the initial-boundary value problem of equation(1.1)had been studied in many papers,many excellent and important results had been obtained in[20-22,23-24]etc.Shall we say,there is not important problem left?I think it is too early to make such a conclusion.Besides the problems related to Prandtl boundary layer theory,sincea(u,x,t)≥0 and may be degenerate in the interior of Ω or on the boundary∂Ω,everyone knows that the boundary value condition(1.3)is overdetermined,there is not an effective method to find a reasonable partial boundary value condition

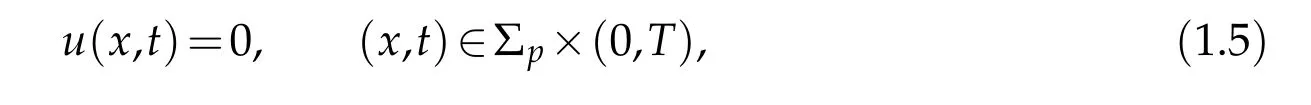
to replace(1.3),where Σpis a relative open subset of∂Ω.Here,we like to suggest that the boundary value condition(1.3)or(1.5)is understood in the sense of the trace,and we expect to find a analytic expression of Σpin this paper. The difficulty comes from that,since the equation has the nonlinearity,the partial boundary Σpin(1.5)can not be depicted out by Fichera function as that of the linear degenerate parabolic equation[25-26].

In fact,for a nonlinear parabolic equation,how to impose a reasonable partial boundary value condition has been up in the air for a long time[20-22,27-29].Let us give some details.In[20-22],the entropy solutions defined in these references are inL∞(QT)sense,one can not define the trace on the boundary,accordingly,it is impossible to express Σpin an analytic formula.Instead,the authors of[20-22]had found a kind of the entropy inequality to imply the boundary value condition(1.5)in ingenious ways.In the work by Yin-Wang[27],the degenerate non-Newtonian fluid equation

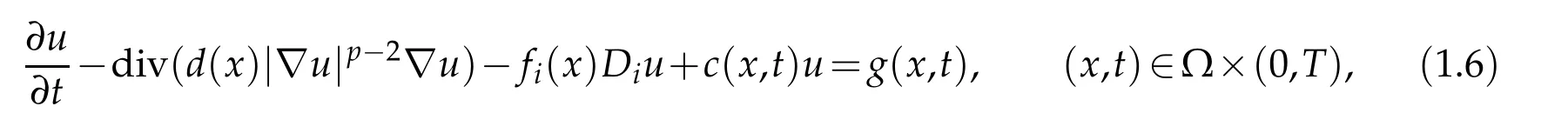
was considered. By means of a reasonable integral description,in[27],the boundary∂Ω is classified into three parts:the nondegenerate boundary Σ1,the weakly degenerate boundary Σ2and the strongly degenerate boundary Σ3.Instead of the usual boundary condition(1.3),a partial boundary value condition(1.5)is imposed,where

It is pity that,since equation(1.1)is apparently different the Non-Newtonian equation(1.6),Σpalso can not be described as(1.7).If the domain Ω is theN-dimensional cube or the half space of RN,the equation

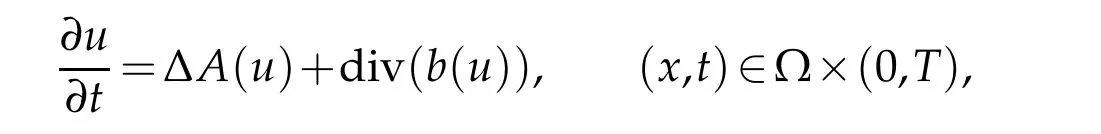
was studied in[28-29]by the author recently,a reasonable analytic expression of Σphad been found in[28-29].However,for a general domain Ω,the problem remains open.We hope to make a essential progress sooner or later.

Certainly,since the subset setD0={x∈Ω:a(·,x,t)=0}may have a positive measure in Ω,equation(1.1)has hyperbolic characteristic inD0.Thus,only in the sense of the entropy solution,the uniqueness(or the stability)of the weak solution can be obtained[1]. In this paper,with the help of the entropy solutions defined in the sense ofBVfunctions[1,11,28,30],we study the well-posed problem of equation(1.1)with the initial value(1.2)and the partial boundary value condition(1.5),the key is to find a reasonable analytic expression of Σpfirst time.

The paper is arranged as follows.After the introduction section,section 2 introduces the definition of the entropy solution and the main results. Section 3 gives the proof of the existence of the entropy solutions.Section 4 introduces the well-known Kružkov bi-variables method.Section 5 is on the stability of the entropy solutions based on the partial boundary value condition. At the end,an explanation of the definition of the entropy solution is given.

2 The definition of the entropy solution and the main results

For the completeness of the paper,we first quote the definition ofBVfunction and its properties[28].

Definition 2.1.LetΩ⊂Rm be an open set and let f∈L1(Ω).Define

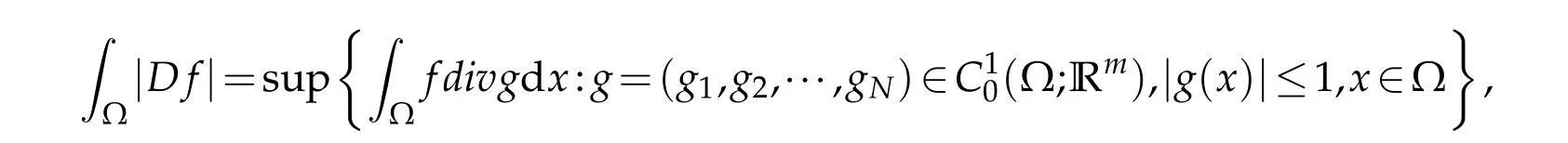
where divg=

Definition 2.2.A function of f∈L1(Ω)is said to have bounded variation inΩif

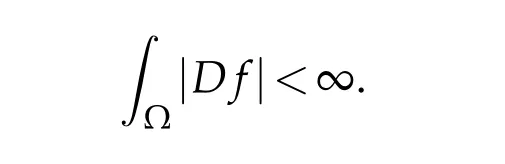
We define BV(Ω)as the space of all functions in L1(Ω)with bounded variation.This is equivalent to that the generalized derivatives of every function in BV(Ω)are regular measures onΩ.Under the norm

BV(Ω)is a Banach space.

Proposition 2.1.(Semicontinuity)LetΩ⊆Rm be an open set and{fj}a sequence of functions in BV(Ω)which converge in(Ω)to a function f.Then

Proposition 2.2.(Integration by part)Let

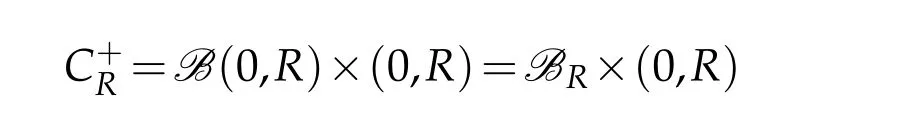
-1-almost all y∈BR,

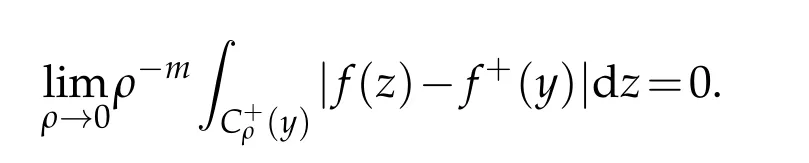
Moreover,if CR=BR×(-R,R)

whereBρ={x∈Rm;|x|＜ρ}.

Remark 2.1.The functionf+is called the trace offon BRand obviously

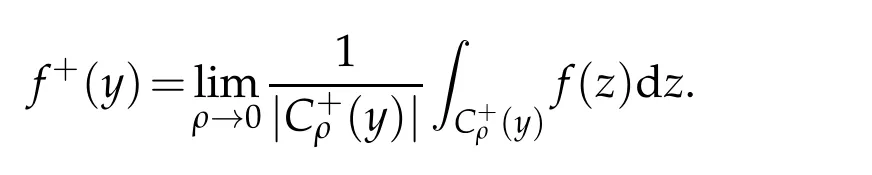
The definition of the trace is easy generalized to a general smooth domain in Rm.Secondly,we give the definition of the entropy solutions matching up with equation(1.1).For smallη＞0,let

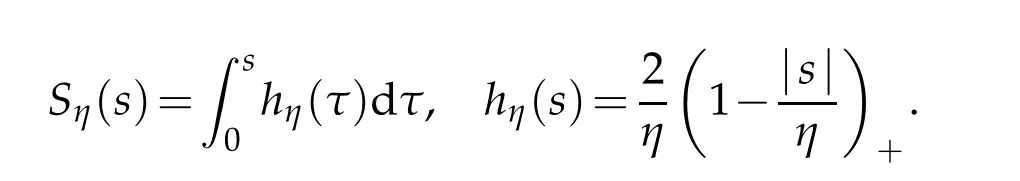
Obviouslyhη(s)∈C(R),and

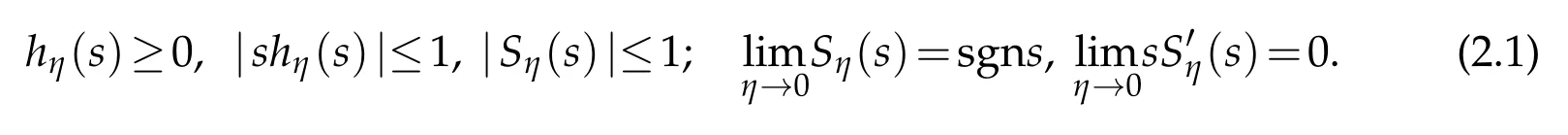
Definition 2.3.(1.1)with the initial value(1.2),provided that

1.There exist gi∈L2(QT)(i=1,2,···,N)such that for any

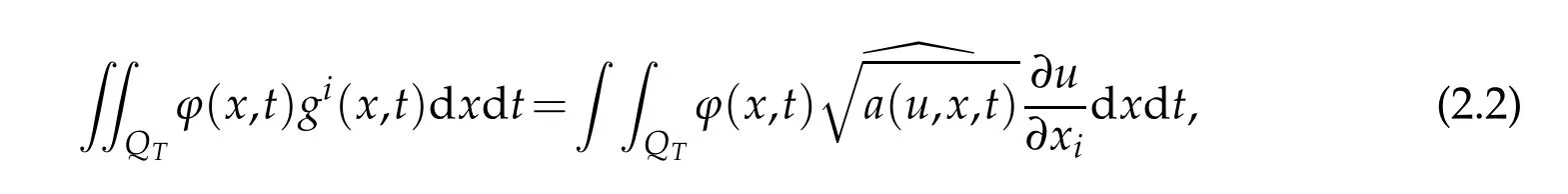
where

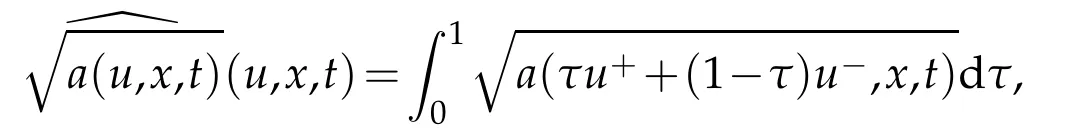
is the composite mean value of

≥0,for k∈Rand for any small η＞0there holds

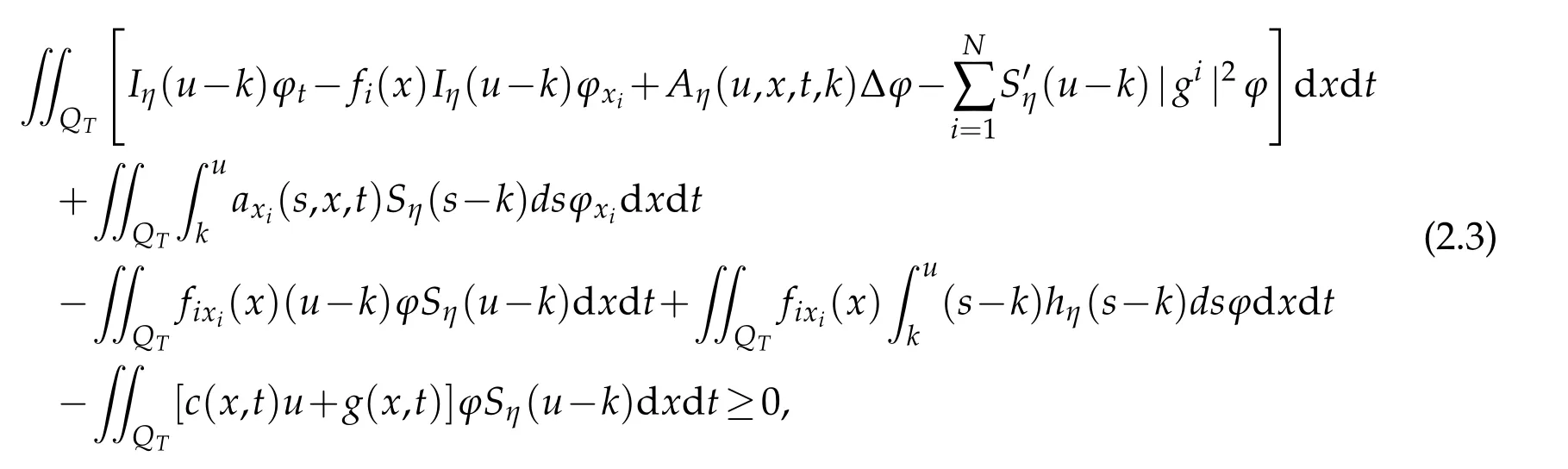
where

3.The initial value is satisfied in the sense of that

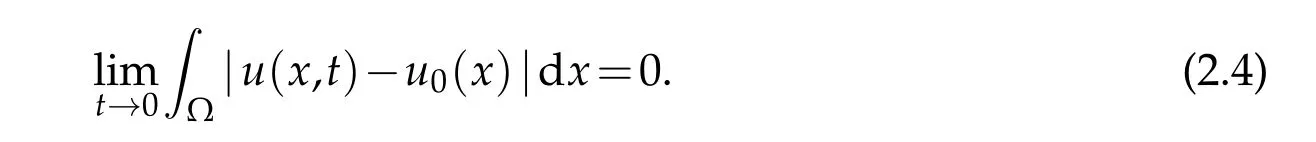
Definition 2.4.If u∈BV(QT)∩L∞(QT)is the entropy solution of equation(1.1)with the initial value(1.2),and the partial boundary value condition(1.5)is satisfied in the sense of the trace,then we say u is a entropy solution of the initial-boundary value problem of equation(1.1).Here,

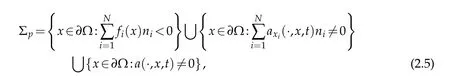
andis the inner normal vector ofΩ.

In what follows,we can show that ifthen Σpin the partial boundary value(1.5)can be depicted out as(2.5). Based on this fact,thirdly,we will prove the following theorems.

Theorem 2.1.Ifc(x,t)and g(x,t)areL∞(Ω),then equation(1.1)with the initial value condition(1.2)has an entropy solution in the sense of Definition2.3.

Theorem 2.2.If a(s,x,t)∈C1(RN×QT)with a(0,x,t)=0,(x,t)∈QT,and g(x,t)areand there is a constant δ1＞0such that

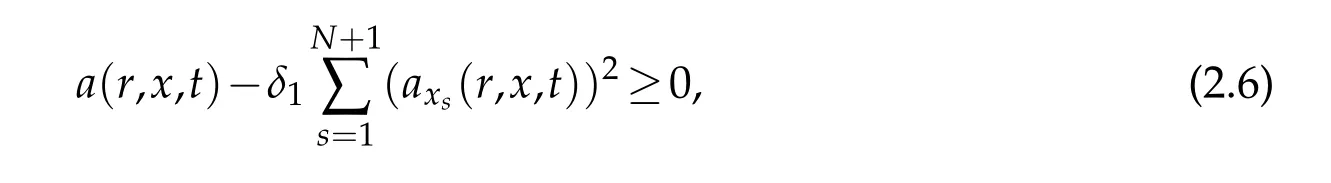
then the initial-boundary value problem of Eq.(1.1)has an entropy solution in the sense of Definition2.4.

Theorem 2.3.Suppose a(·,x,t)(s,x,t)is bounded when s is bounded,c(x,t)and g(x,t)are bounded.Suppose that when x is near to the boundary,

there exist constants δ2＞0such that

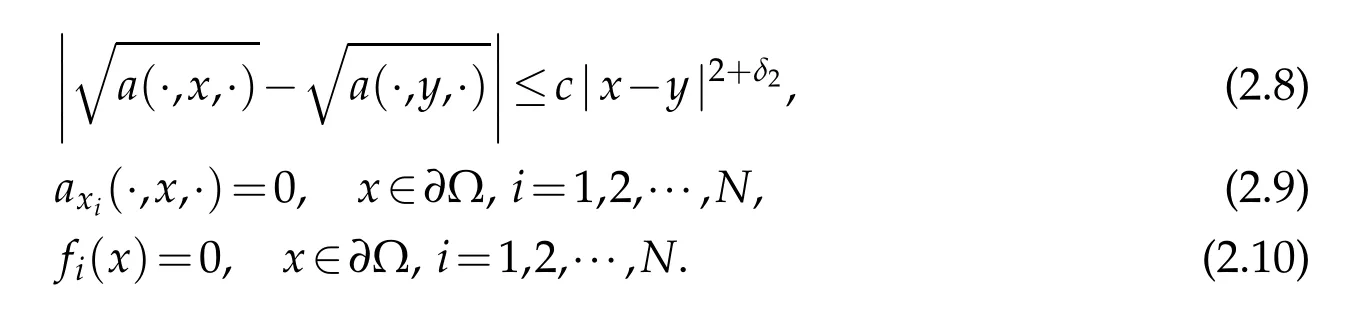
If u(x,t)and v(x,t)are two solutions of Eq.(1.1)with the different initial values u0(x),v0(x)∈L∞(Ω)respectively,then

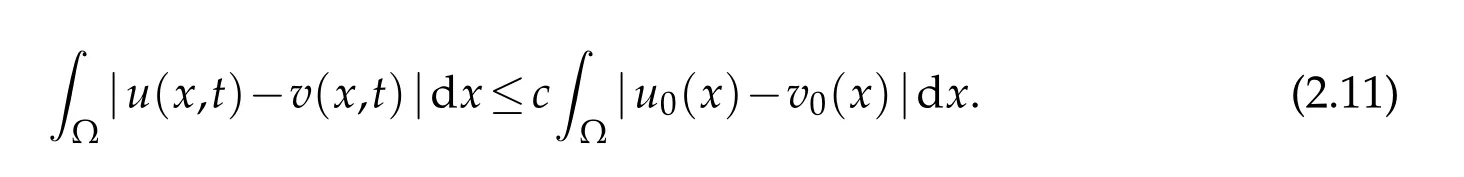
Here d(x)=dist(x,∂Ω)is the distance function from the boundary,a(·,x,t)is regarded as the function of the variables(x,t),a(·,x,·)is regarded as the function of x.

In general,the conditions listed in Theorem 2.3 are only the sufficient conditions,and can be replaced by the other assumptions.

If without the condition(2.7),we have

Theorem 2.4.Suppose that a(·,x,t)(·,x,t)|x∈∂Ω=0,a(s,x,t)is bounded when s is bounded,,c(x,t)and g(x,t)are bounded. Suppose that the conditions(2.8)-(2.10)are true.If u(x,t)and v(x,t)are two solutions of Eq.(1.1)with the different initial values u0(x),v0(x)∈L∞(Ω)respectively,thenthe stability(2.11)is true.

If the condition(2.10)is not true,we have the following stability based on the partial boundary value condition(1.5)with Σpappearing as(2.5).

Theorem 2.5.Suppose a(·,x,t)(s,x,t)is bounded when s is bounded,c(x,t)and g(x,t)are bounded.Suppose that the condition(2.7)is true.If u(x,t)and v(x,t)are two solutions of Eq.(1.1)with the different initial values u0(x),v0(x)∈L∞(Ω)respectively,and with the same partial boundary value condition

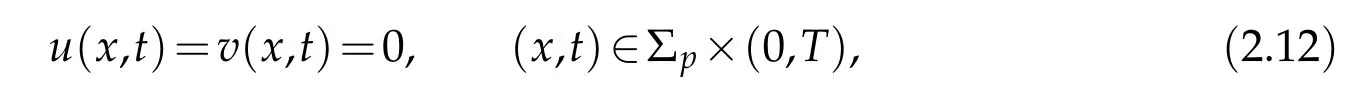
then the stability(2.11)is true,whereΣp has the form(2.5).

Now,we give a simple comment on Theorem 2.4 and Theorem 2.5. For the linear degenerate parabolic equation

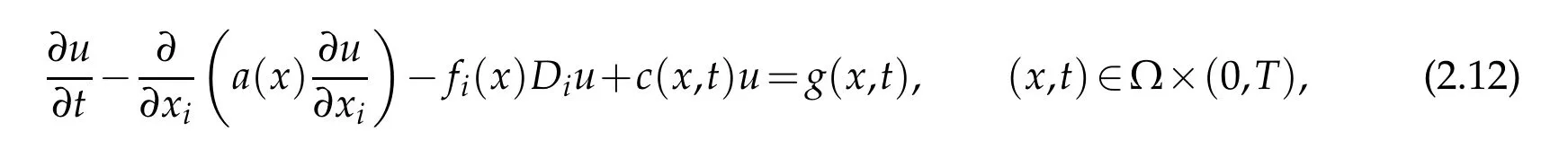
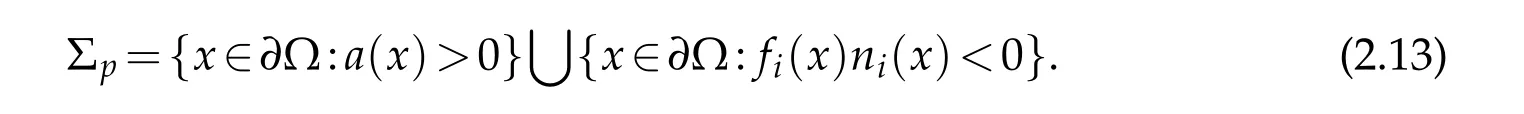
Ifand the condition(2.10)is imposed,by(2.14),we have

In the other words,the stability of the weak solutions of equation(2.13)can be obtained independent of the boundary value condition.This coincides with Theorem 2.4.

If without the condition(2.10),since(2.14)reduces to the expression(2.5).This coincides with Theorem 2.5.

Fourthly,we would like to suggest that there are many domains satisfying the condition(2.7).For examples,

i)TheN-dimensinoal cube

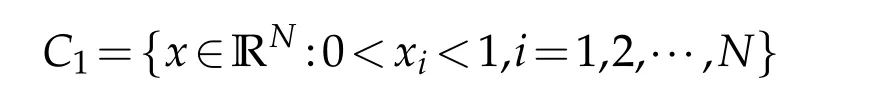
the distance functiondfrom the boundary satisfies that whenxis near to the hyperplane{x:xi=0},

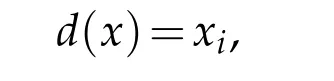
whilexis near to the hyperplane{x:xi=1},

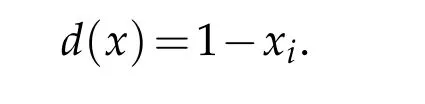
ii)TheN-dimensional unit disc

the distance function from the boundary is

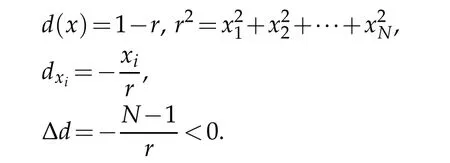
The last but not the least,we have said before the condition(2.7)is not a necessary condition.For example,in Theorem 2.4,we have used the conditionto replace the condition(2.7).This is very interesting phenomena.Condition(2.7),Δd＜0 reflects the geometric characteristic of the domain Ω,while,a(·,x,t)itself is the diffusion coefficient,the conditionimplies the diffusion process ends at the boundary∂Ω.The results of our paper show that these two different conditions both are enough to make the solutions stable.

3 The proof of the existence

The existence of the entropy solutions of equation(1.1)can be proved by the similar way as that in[28,29,32],we only give the outline of the proof in what follows.

Lemma 3.1.([33])Assume thatΩ ⊂RN is an open bounded set and fk,f∈Lq(Ω),as k→∞(Ω)(1≤q＜∞).Then we have

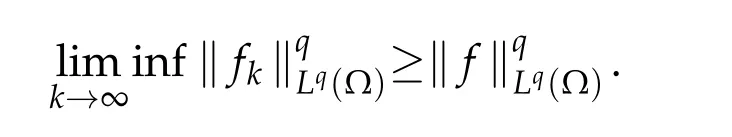
Proof.Proo f o f Theorem2.1 Consider the regularized problem

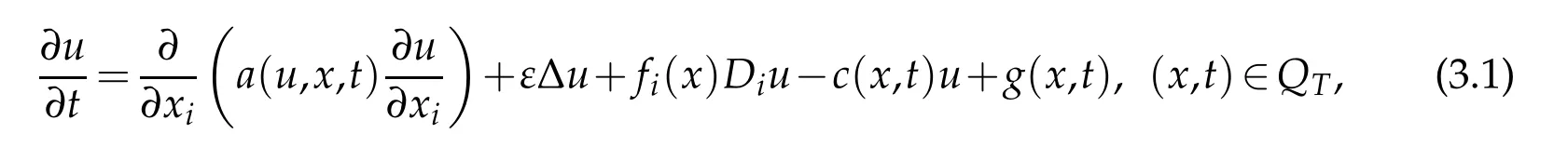
with the initial-boundary conditions

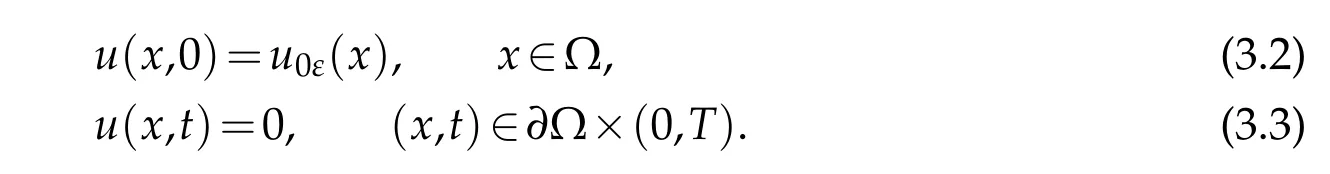
Here,u0ε(x)is a mollified function ofu0.We know that there exists a classical solutionsuε,provided that botha(u,x,t)andbi(u,x,t)satisfy the assumptions given in Theorem 2.1.For more details,one can refer to[5]or Chapter 8 of[25].Moreover,we have

Step 1Multiplying equation(3.1)withuε,it is easy to show that

usatisfies(1)of Definition 2.6.

Step 2LetMultiplying both sides of(3.1)byintegrating it by part,we can deduce that

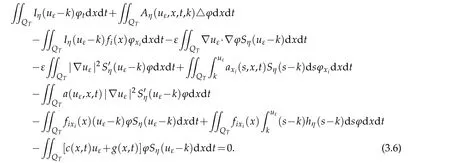
By Lemma 3.1,we have

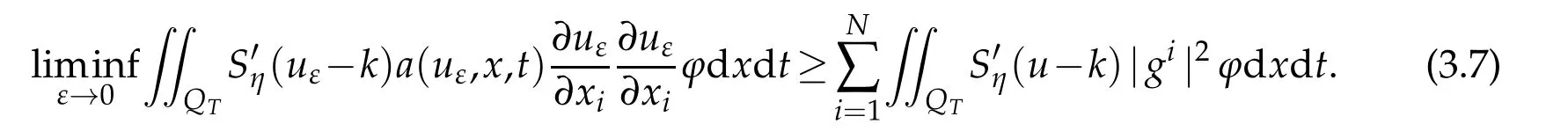
Lettingε→0 in(3.6),it is easily to obtain(2.3).

Step 3At last,the initial value(1.2)is true in the sense of(2.4),its proof can be found in[34].

Thus,the existence of the entropy solution in the sense of Definition 2.6 has been proved,Theorem 2.1 follows immediately.

Lemma 3.2.Let uε be the solution of the problem(3.1)-(3.3).If the assumptions given in Theorem2.2hold,then

where c is independent of ε,and

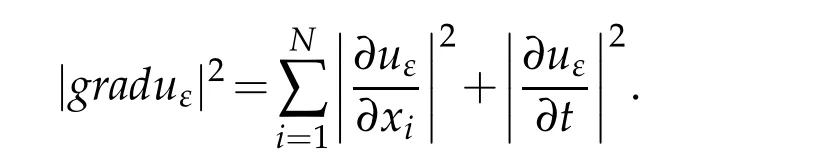
Lemma 3.2 can be proved in a similar manner as Theorem 11 of[29],we omit the details here.

By Theorem 2.1 and Lemma 2.2,we know that Theorem 2.2 is true.

4 Kruzkov’s bi-variables method

Similar as[1,22],we denote that Γuis the set of all jump points ofu∈BV(QT),vis the normal of ΓuatX=(x,t),u+(X)andu-(X)are the approximate limits ofuatX∈Γuwith respect to(v,Y-X)＞0 and(v,Y-X)＜0,respectively.For the continuous functionsp(u,x,t)andu∈BV(QT),the composite mean value ofpis defined as

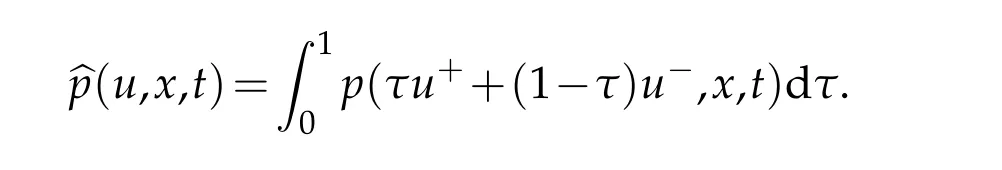
Iff(s)∈C1(R)andu∈BV(QT),thenf(u)∈BV(QT)and

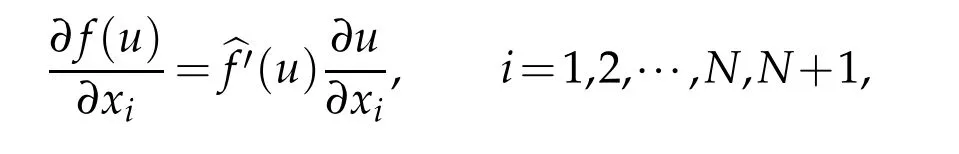
wherexN+1=t.

Lemma 4.1.Let u be a solution of(1.1).Then

which I(α,β)denote the closed interval with endpoints α and β,and(4.1)is in the sense of Hausdorff measure HN(Γu).

Proof.Denote

At first,we provea(s,x,t)=0,s∈I(u+(x,t),u-(x,t))a.e.onΓ1.Since any measurable subset of Γ1can be expressed as the union of Borel sets and a set of measure zero,it suffices to prove

whereUis a Borel subset of Γ1.For any bounded functionf(x,t),which is measurable with respect to measureLemma 3.7.8 in[1]shows that

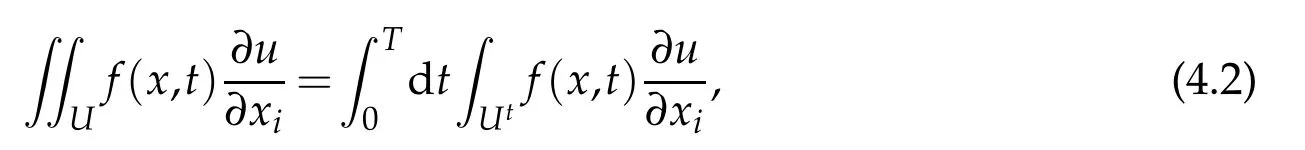
whereMoreover,for any Borel subsetfori=1,2,···,N,

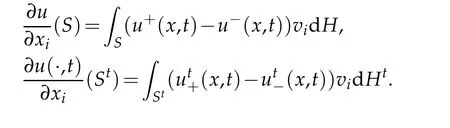
(4.2)is equivalent to

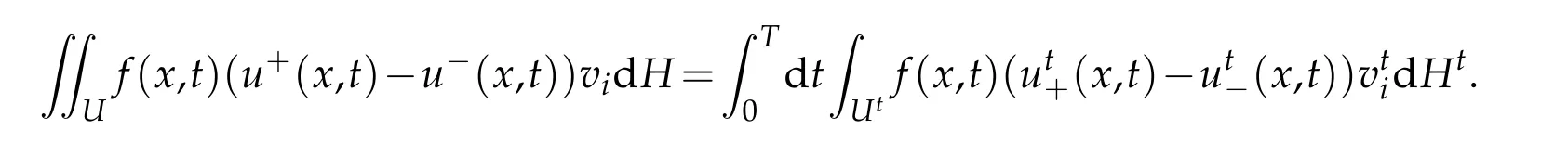
The definition of Γ1implies that the left hand side vanishes,then

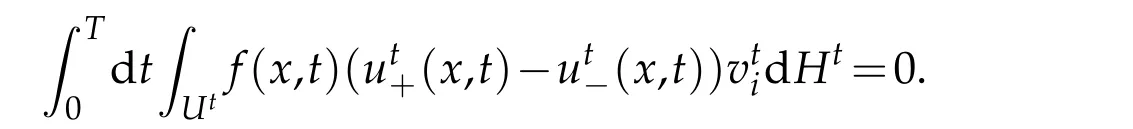
If we choosewhereχu(x,t)is the characteristic function ofU,sum up forifrom 1 up toN,then

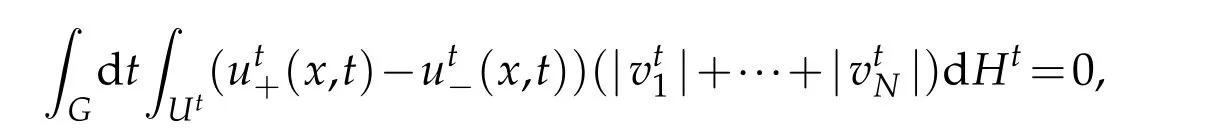
whereGis the projection ofUon thet-axis.(4.2)implies for almost allt∈G,

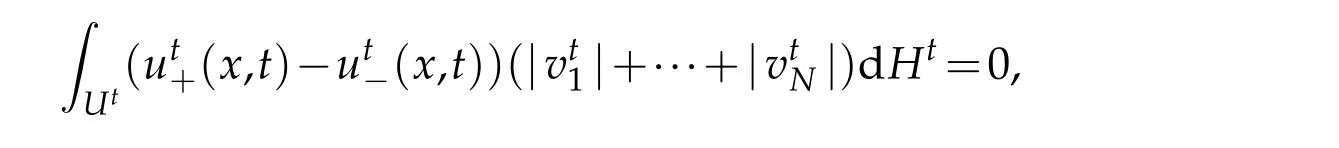
and hence for almost allt∈G,

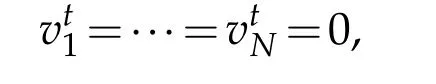
Ht-almost everywhere onUt,which is impossible unless mesG=0.

For anyα,βwith 0＜α＜β＜T,we choosesuch that

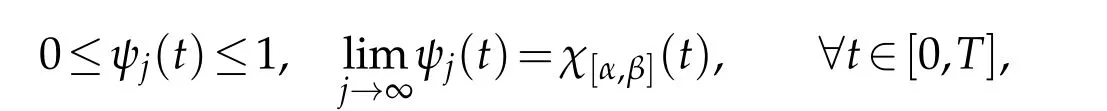
and choosesuch that

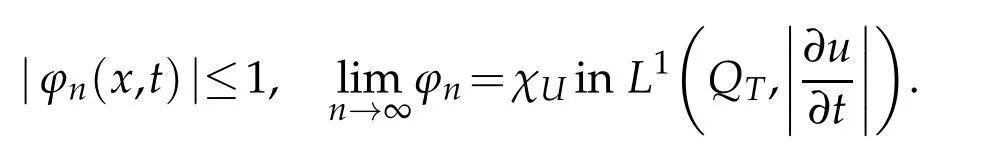
Now,denoting that

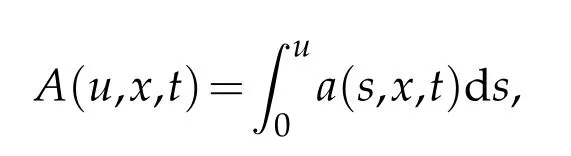
from the definition of BV-function,we have

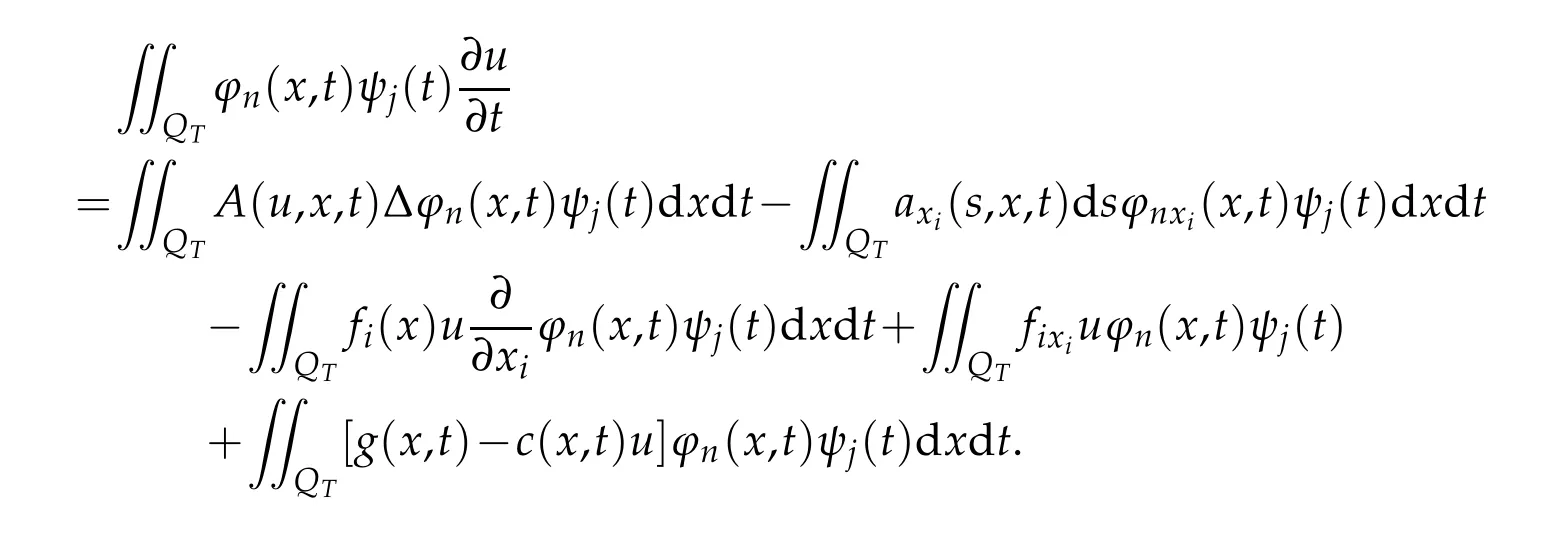
Letj→∞.Then

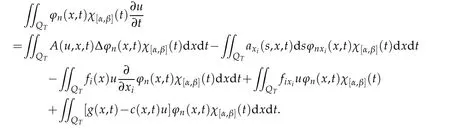
Clearly,this equality also holds if[α,β]is replaced by(α,β)and hence it holds even if[α,β]is replaced by any open setIwith.SinceGis a Borel set,by approximation we may conclude that

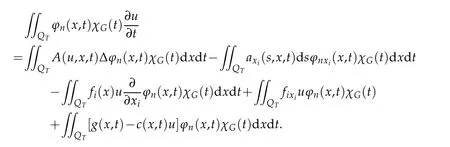
The two terms on the right hand vanish by that mesG=0,and

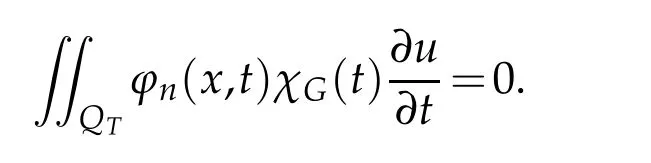
Letn→∞.Then

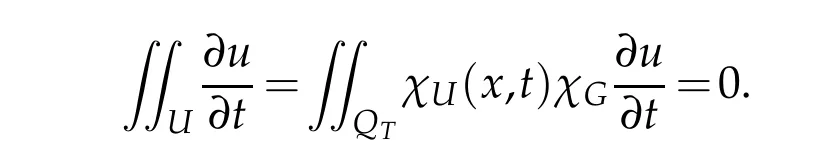
Hence

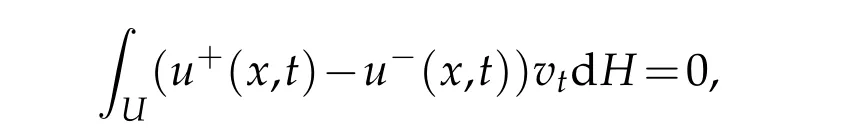
which impliesH(U)=0 andH(Γ1)=0 by the arbitrariness ofU.

Secondly,we proveH(Γ2)=0.LetUbe any Borel subset of Γ2which is compact inQT.SinceUis a set ofN+1-dimensional measure zero andwe have

and hence

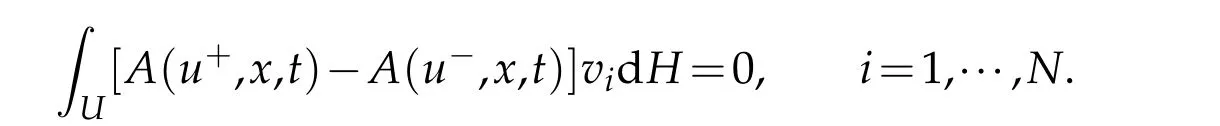
Form this fact,it follows by the definition of Γ2that

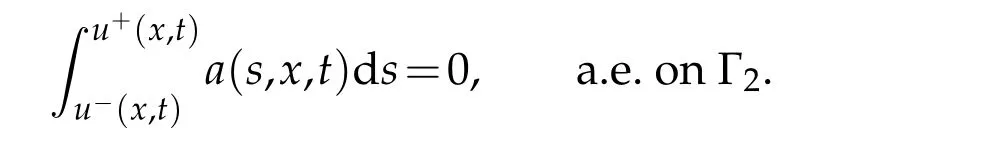
Thus the lemma is proved.

In this section,we apply Kružkov bi-variables method to the main equation(1.1).In details,letu(x,t)andv(x,t)be two entropy solutions of equation(1.1)with the initial values

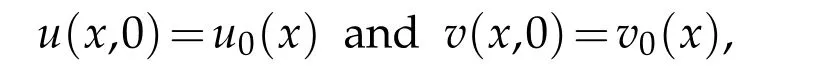
respectively.

By Definition 2.6,for any nonnegativewe have

and

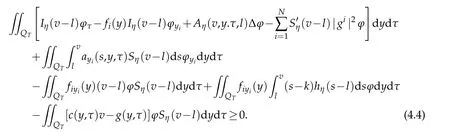
Let

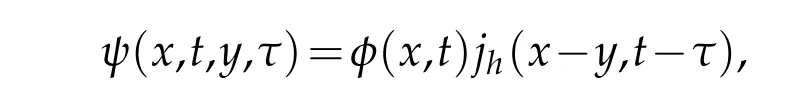
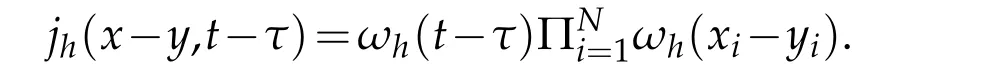
We choosek=v(y,τ),l=u(x,t)andφ=ψ(x,t,y,τ)in(4.3)and(4.4).Integrating it overQT,using the fact of thatSη(u-v)=-Sη(v-u),we have

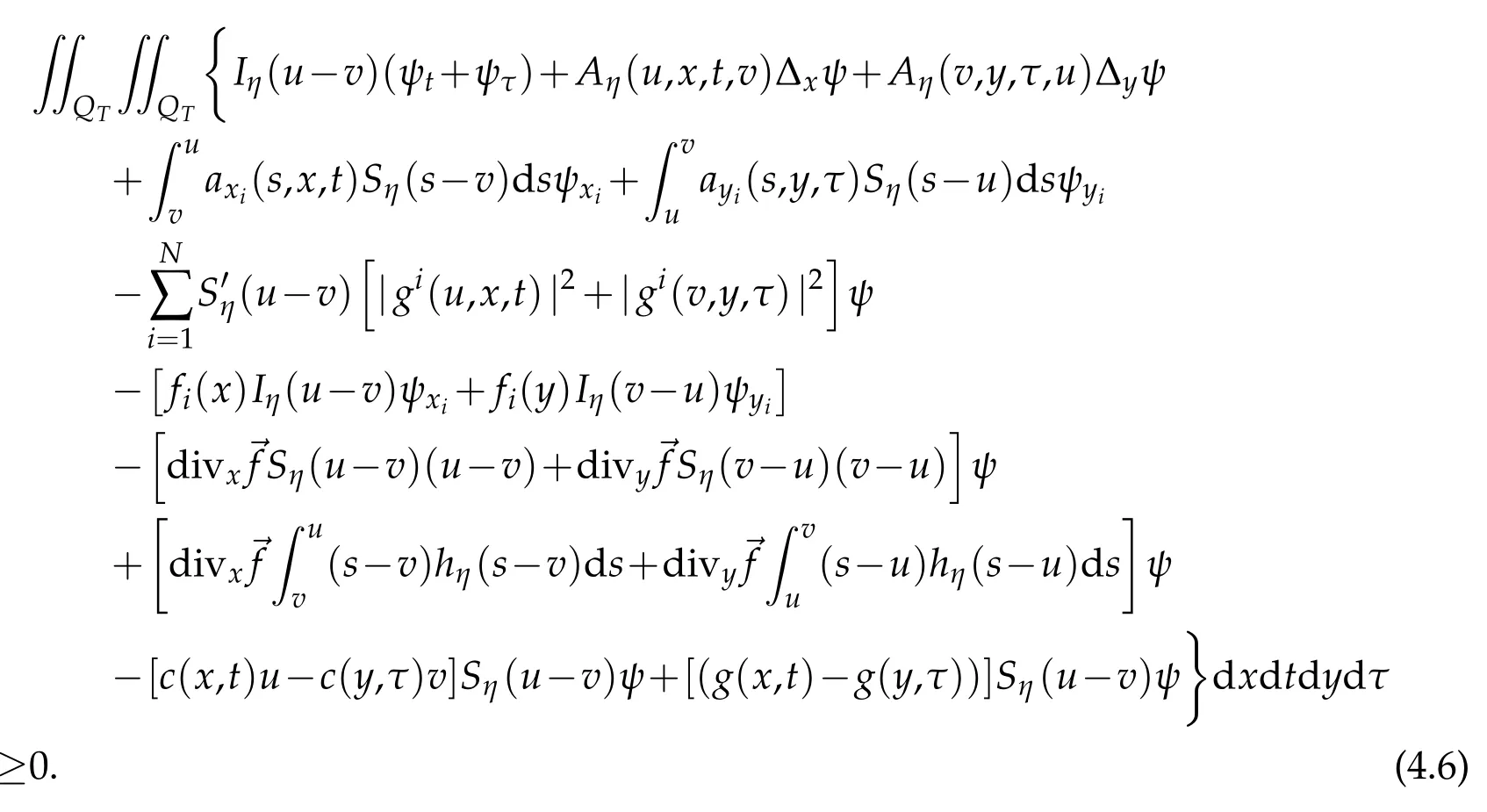
We can use the facts

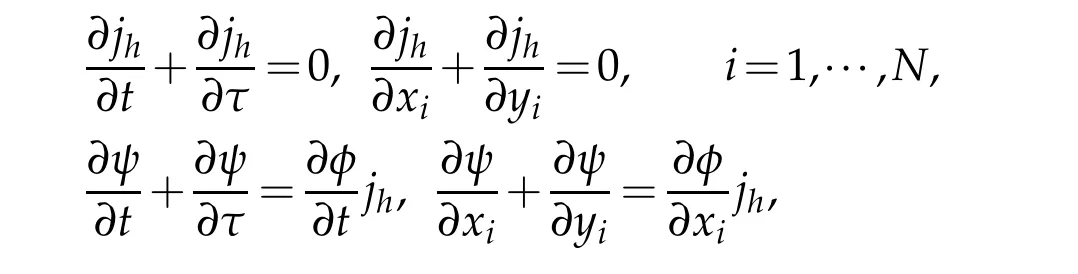
to analysis every term of the left hand side of(4.6).

The first term,we have

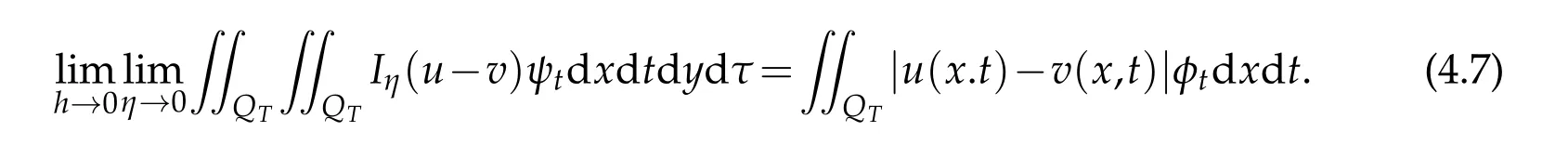
From the second term to the sixth term,by a very complicated calculations[32],by(4.1)in Lemma 4.1,using the condition(2.8)and the observation(4.5),we can deduce that

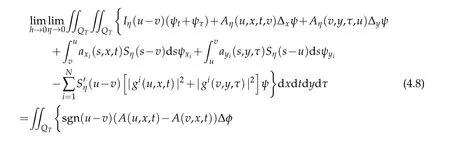
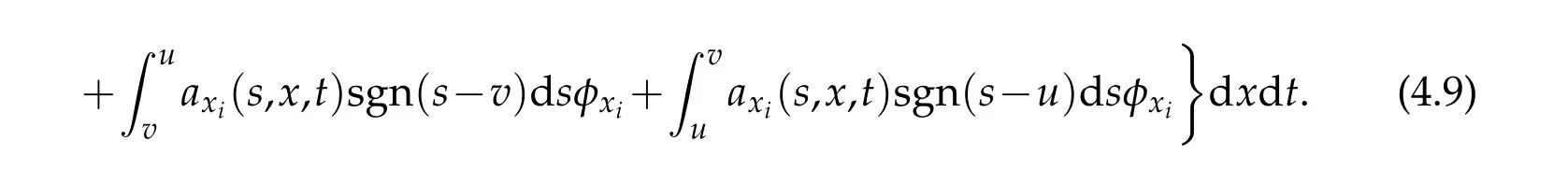
For the seventh term,by the fact

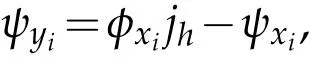
we have

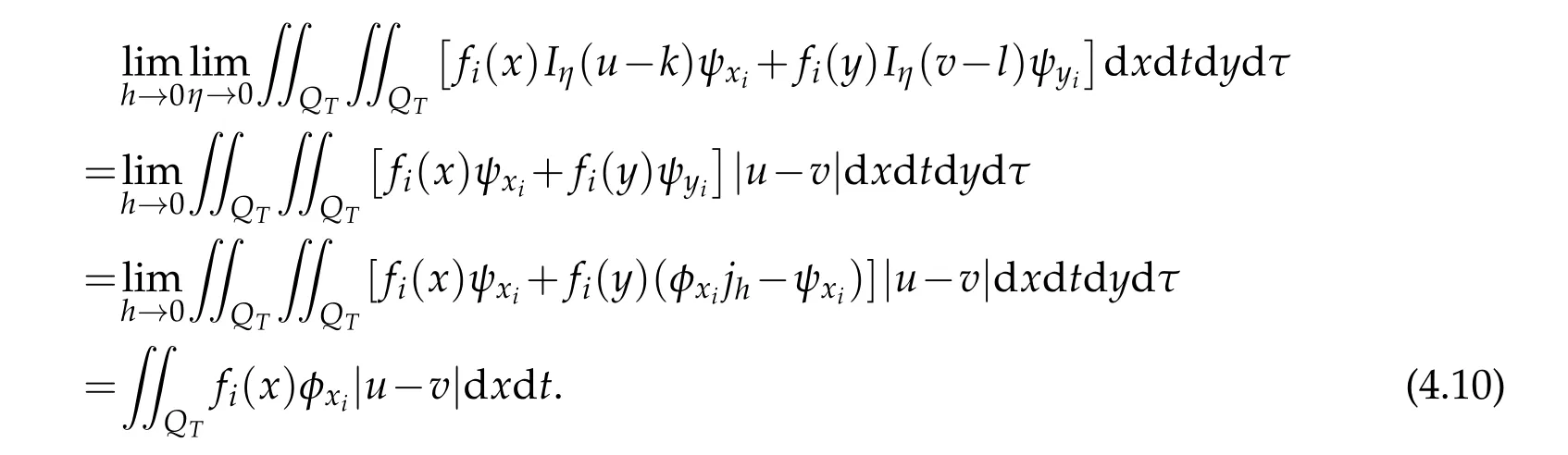
For the eighth term,it is obviously

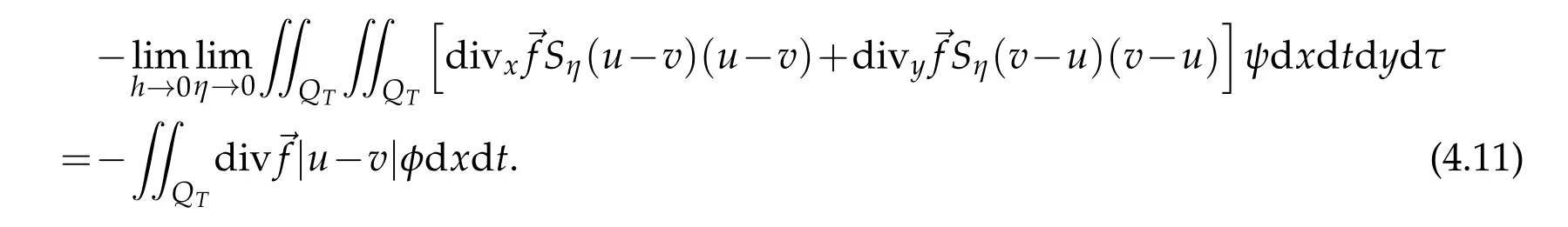
For the ninth term,it is obviously

For the tenth term,

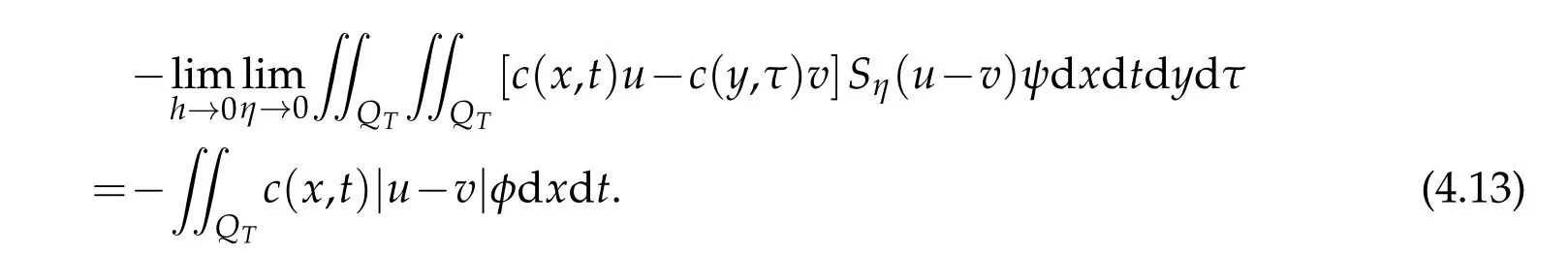
For the last term,

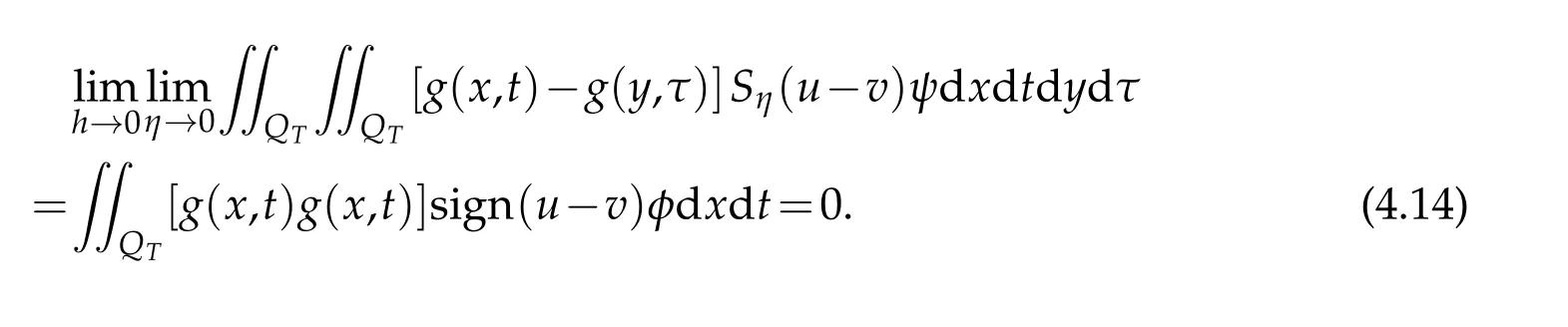
Thus,if we letη→0 andh→0 in(4.6),then we have

By choosing some special test functions or some special domains Ω,one can prove the stability of the entropy solutions according to(4.14).

5 Proof of Theorems 2.3–2.5

5.1 Proof of Theorem 2.3

For small enoughλ,we define

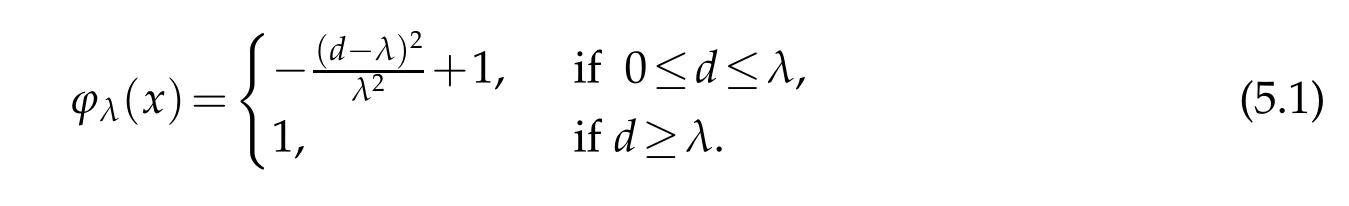
By a process of limit,we can choose the test function in(4.14)as

While in ΩΩλ,

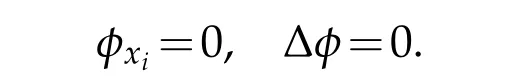
In the first place,by the assumption of that Δd≤0,choosingλis small enough,whenxis near to the boundary,d(x)＜λ,we have

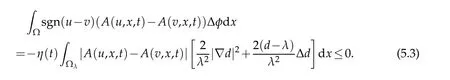
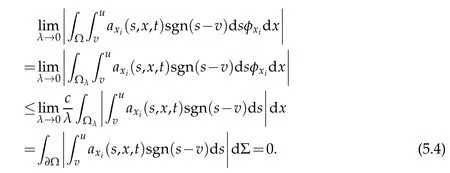
Similarly,we have

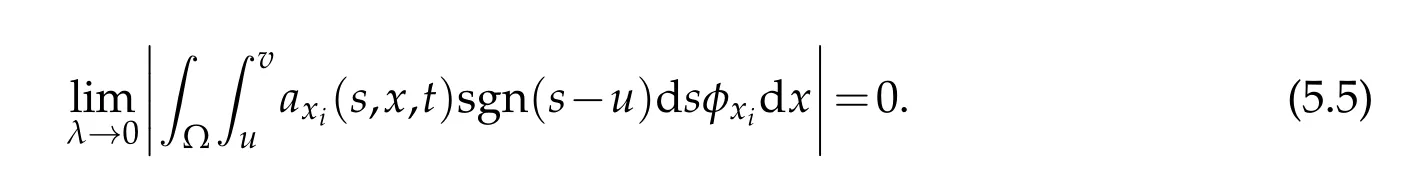
Moreover,by that|dxi|≤|∇d|=1,and by the assumption of thatfi(x)=0 whenx∈∂Ω,we have

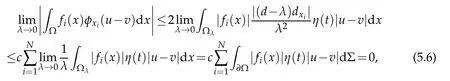
and it is clearly that

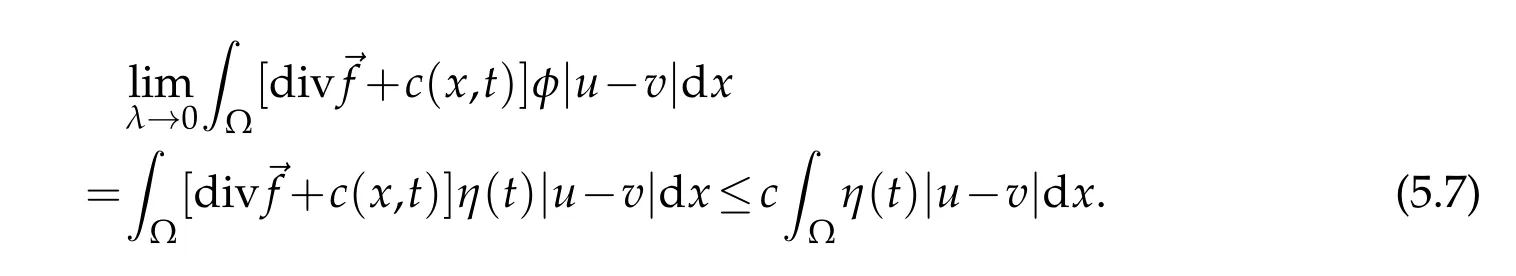
By(5.3)-(5.7),according to(4.12),we have

Let 0＜s＜τ＜T,and

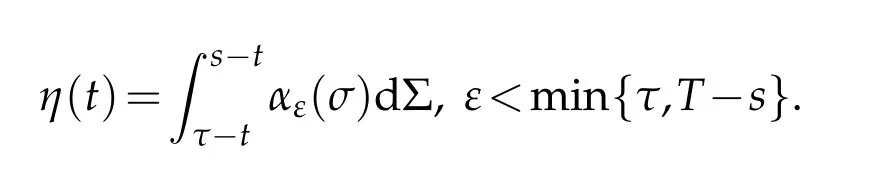
Hereαε(t)is the kernel of mollifier withαε(t)=0 forThen

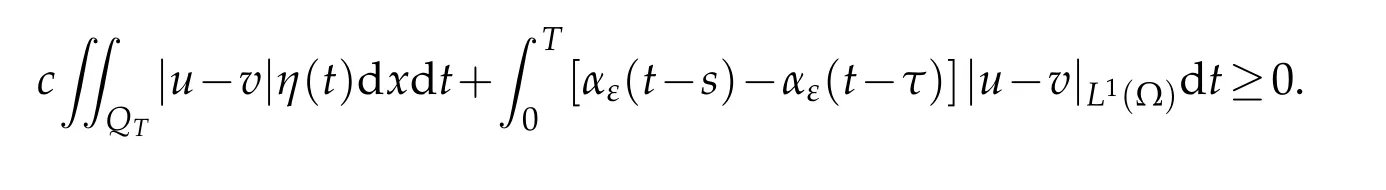
Letε→0.Then

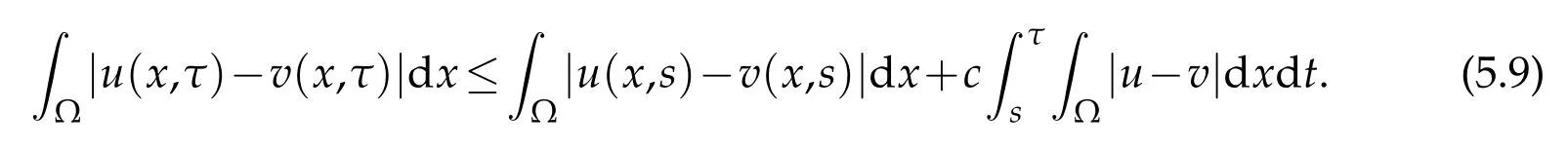
By the Gronwall inequality,we have

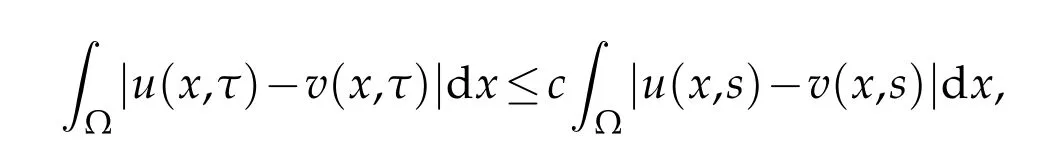
lettings→0,we have the conclusion.

5.2 Proof of Theorem 2.4

From proof of Theorem 2.3,we only need to deal with the term

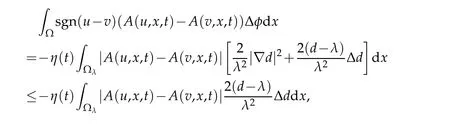
we have

Then we have the conclusion.

5.3 Proof of Theorem 2.5

Since we have imposed the partial boundary value condition

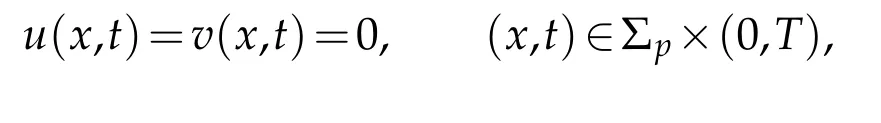
with

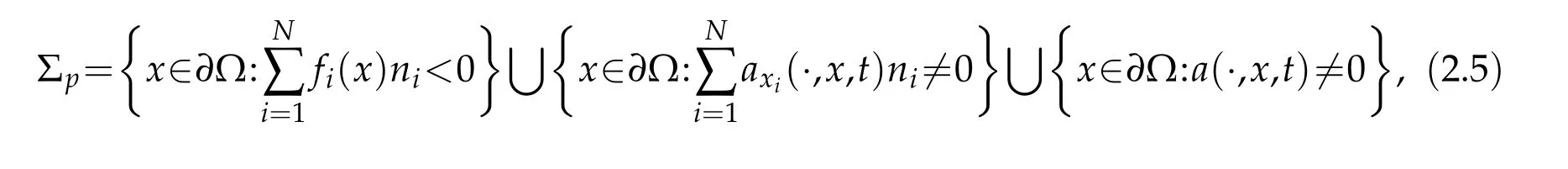
From proof of Theorems 2.3–2.5,we know(5.4),(5.5)and(5.10)are still true.We only need to deal with the term

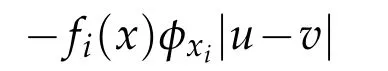
in(4.12).In other words,since there is not the condition(2.10),the inequality(5.6)is not true.Actually,by the partial boundary value condition(2.12)with the expression(2.5),if we denote that

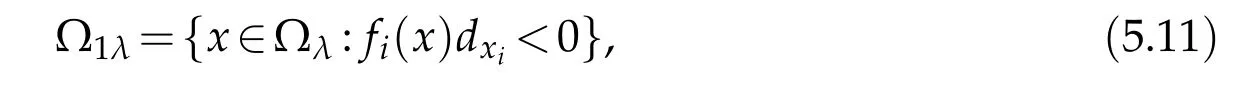
then we have

Similar as the proof of Theorem 2.4,we have the conclusion.

6 The explanation of Definition 2.3

Let us give a simple explanation of Definition 2.3 lastly.

Letuεbe the solution of the regularized equation

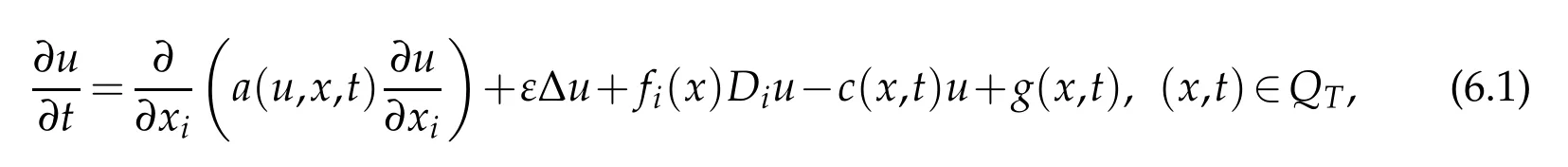
with the initial-boundary value conditions(3.2)-(3.3).Multiplying both sides of(6.1)byφSε(uε-k)and integrating it overQTyields

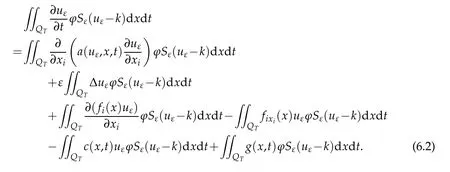
Integration by parts,(6.2)gives

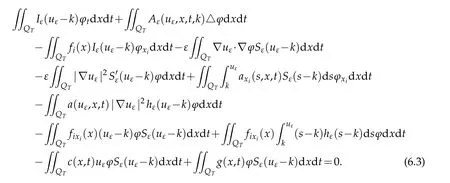
By discarding the terms

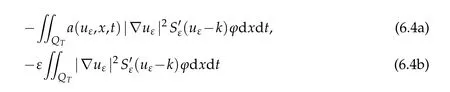
in(6.3),we have

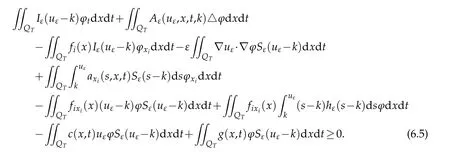
Letε→0.We can get

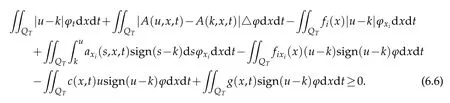
The inequality(6.6)is just the classical entropy inequality used in[9,11]etc.However,the term(6.4)can not be thrown away casually.In fact,this term includes many information of the uniqueness[15-18,28-29,30,32,34-35].The difficulty lies in that,when we letε→0,what is the limit of the term(6.4)is very difficult to depict out,so it is almost impossible to remain the limit to the end,one has to throw it away[9,11].

In order to overcome this difficulty,instead of multiplying both sides of(6.1)byφSε(uε-k),we multiply both sides of(6.1)byφSη(uε-k),whereηis a small positive constant independent ofε.Then we can employ the weak convergent theory(Lemma 3.1),the uniqueness information of the term(6.4)remains,and we can prove the uniqueness of the entropy solutions by Kružkov’s method.

Acknowledgement

The paper is supported by Natural Science Foundation of Fujian province(2019J01858),and supported by SF of Xiamen University of Technology,China.The author would like to think reviewers for their good comments.