基底隔震的多层建筑结构自振频率和振型解析
丁肇伟,陈龙珠,李庆来
(1.上海交通大学 船舶海洋与建筑工程学院 安全与防灾工程研究所,上海 200240; 2.上海东浩兰生(集团)有限公司,上海 200040)
地震是造成我国人员伤亡最为严重的一种自然灾害。根据国内外科学研究和工程实践的成果,我国于2001年修订实施的《建筑抗震设计规范》(GB 50011-2001),已涵盖了抗震、隔震和消震3大类地震防御技术[1-3]。定性来说,抗震技术适用于各种建筑结构,隔震技术多用于刚度较大、高宽比较低的多层和高层建筑,而消震技术则适用于相对柔性的结构或结构中动力响应较大的部位。基底隔震技术是通过水平刚度低且具有一定阻尼的隔震器,在上部结构与基础之间实现水平方向的柔性连接,使得由地基输入上部结构的地震能量及其产生的加速度大为降低,结构层间位移大幅减小而不易损坏和坍塌,由此大幅提高建筑结构对强烈地震的防御能力。
我国自1994年建造首座采用橡胶支座的基底隔震示范建筑[4]以来,这个地震防御技术已得到了很好的推广应用。在2008年5月汶川八级地震中,甘肃省陇南市武都区采用了基底隔震技术的北山邮政职工住宅楼完好无损,但邻近普通的多层房屋结构墙体却普遍出现了开裂[5]。四川省芦山县人民医院门诊综合楼[6],地上6层,局部地下1层,建筑设防类别为乙类,设防烈度为Ⅶ度(0.15g),设计地震分组为第2组,中硬场地土,属于Ⅱ类场地。2013年4月芦山七级地震时,该楼隔震效果显著,是我国到目前为止已被Ⅸ度实际地震考验的隔震建筑。另一方面,早期建造的部分既有隔震建筑已出现不同程度病害,为了评价隔震层及隔震建筑动力特性现状,需要研究此类建筑的检测与鉴定方法[7]。
建筑隔震设计可采用地震反应谱法和时程分析法,前者涉及结构自振频率和振型,后者需要采取数值积分计算[8]。在土木工程结构动力学中,对于多于3个自由度的建筑结构,自振频率和振型的计算,因涉及高阶超越方程而采用数值计算或近似简化理论方法[9-10]求解,这对工程设计已不构成困难,但不便于直观地了解自振频率和振型受隔震层刚度、上部结构各层刚度和质量的影响方式。对在地基简谐运动激励下的多自由度结构,文献[11]采用复数法直接得到了结构动力响应幅频关系的解析解,由此可作为参数分析考察基底隔震层参数的变化对上部结构层间位移分布特性的影响规律。
三对角Toeplitz矩阵的主对角线和2个次对角线上的元素各自为一个常数,其余位置上的元素全为0。文中参考这种特殊矩阵的特征值和特征向量的解析求法[12-13],先对多层建筑结构基底隔震层刚度取2个特定数值条件下的各阶自振频率和振型求得解析解,然后求其他数值的基底隔震层刚度,由此假设其各阶自振频率和振型的解析函数,再通过对数值计算结果的拟合分析,检验是否为自振频率和振型的精确表达式。
1 特殊条件下结构自振频率和振型解析解
图1为模拟基底隔震的6层水平剪切型建筑结构计算简图。由于其底层下方设置了可水平向大幅变形的隔震层,该基底隔震的6层建筑结构在水平方向上具有7个自由度。假设各层楼板和屋面凝聚的质点质量相同(记为m),上部结构各层的水平刚度相同(记为k),隔震层刚度为αk,其中α为隔震层刚度比。改变α值,便可观察基底隔震层刚度对隔震建筑结构自振频率及其振型的影响。
图1所示结构的特征方程可以表示为:

图1 6层基底隔震建筑计算简图Fig.1 Calculation of six-story base-isolated building
(1)
式中:λ=ω2m/k,(ω为振动圆频率);φ为振型列阵。H为三对角矩阵:
由于三对角矩阵H,其主对角线上的元素并不全部相同,不是经典的Toeplitz三对角矩阵的形式。因此,对任意的α值,不能直接套用其特征值和特征向量的解析公式来求解结构各阶自振频率和振型。采用求解三对角Toeplitz矩阵特征值和特征向量的数学方法,式(1)难以得到解析解。作为一个特例,取α=1,则式(1)可以展开为递推式和边界条件:
(2)
对式(2)第1行的方程,试取其解为φj=rj,则有rj+1-(2-λ)rj+rj-1=0,经整理后得r2-(2-λ)r+1=0。记这个二元一次方程的2个根为r1和r2,则有:
r1+r2=2-λ,r1r2=1
(3)
所以,式(2)第1行的线性递推式之解可表示为:
(4)
式中β1和β2为待定常数,j=1,2,…,7。
将式(4)代入式(2)第2行的2个边界条件,得:
(5)
由式(3)、(5)得:
(6)
式(6)的解为:
(7)
将式(7)代入式(3)中的第1式,整理得:
(8)
从而得到当α=1时,图1所示7自由度结构第s阶自振圆频率和振型的解析算式:
(9)
(10)
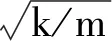
另一个特例,当α=0时(相当于6层建筑漂浮于水中),经过上述类似推导,可得到该情况下,建筑物结构各阶自振圆频率和振型解析算式(s,j=1,2,…,7):
(11)
(12)
2 任意基底隔震刚度下结构自振频率和振型算式
改变基底隔震刚度数值,α乃至H中的主对角线第1个元素的数值发生变化,从而改变结构的自振频率和振型,但此时却不易求出它们的解析解。现根据上述2个特例的理论结果,对任意α值对应的各阶自振频率及其振型,尝试采用如下表达形式:
(13)
(14)
上述2个尝试性算式的误差或适用性检验步骤如下:
1)利用常规数值方法,计算得到任意α值对应的结构自振圆频率和振型;
3)将求出的θαs代入式(14),得到尝试的振型曲线,并将其与第1步中求得的振型曲线进行比较,由相对误差大小来判定尝试性算式的适应程度。

(15)
取α=0.03~1.0内的多个数值,经上述拟合分析得知,由数值方法计算的第1阶自振圆频率和式(13)求出的θα1(图2,表1)以及用尝试性算式(14)得出的第1阶振型(图3),与数值方法所得结果的相关系数均大于0.999,表明式(13)~(15)是精确的表达式。

图2 θα1~α关系曲线Fig.2 Relation curves of θα1~α

表1 θαs与α的关系Table 1 Relation of θαs and α rad
在图3中,α=∞相当于一个6自由度的抗震结构。采用与上节α=1同样的方法,可得其各阶自振圆频率和振型的解析算式:

图3 第1阶振型拟合曲线Fig.3 Fitting curves of the first mod
(16)
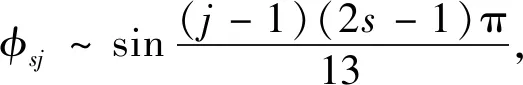
(17)
式(17)仍采用图1的质点编号,取s=1便可绘制归一化的第1阶振型曲线。
由图2可知,当α由1.0逐渐减小到约0.5时,θα1乃至基底隔震结构第1阶自振圆频率才会随α的进一步减小而加速降低。由图3可见,当α减小到0.3时,(Φ17-Φ11)已降低到抗震结构(α=∞)的1/2,而当α取为0.1时,(Φ17-Φ11)约只有抗震结构的1/4。因此,相对于上部结构的层间刚度,隔震层刚度必须足够低,才可能使得上部结构的层间位移大幅降低而接近于刚体平移,从而提高上部结构的地震防御能力。
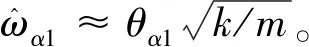

(18)
图2虚线表明,式(18)拟合效果良好:α=0~0.7,相对误差小于1%;在α=1处的相对误差最大,但也低于3.1%。
(19)
将式(18)代入式(14),则可方便地计算出基底隔震结构第1阶振型。
对于α≤1.0,表1表明,各阶自振圆频率数值均未出现sin(0.5θαs)>1的无解问题,即式(13)、(14)适用。
3 结论
1)借用三对角Toeplitz矩阵特征值问题的求解方法,推导了2种特定的隔震层刚度条件下各阶自振圆频率和振型的解析解,由此构造的任意隔震层刚度条件下的结构各阶自振圆频率和振型的解析算式,并用数值解的结果进行了验证。
2)鉴于其对基底隔震建筑结构的地震响应具有重要的影响,分析提出了第1阶自振圆频率和振型的简化算式,具有较高的精度,可用于工程设计中选定隔震层刚度。
3)参数分析表明,当隔震层刚度比α<0.1时,上部结构第1振型的累积层间位移仅约为抗震结构的1/4,已向刚体平动靠近,有利于提高结构的地震防御能力。
本文理论分析的方法可用于求解具有其他层数的基底隔震建筑结构的各阶自振圆频率和振型。

