求解FDCP模型问题的ABC算法

肖 宁,王 鑫

(1.陕西职业技术学院 人工智能学院,西安 710100; 2.太原科技大学 系统仿真与计算机应用研究所,太原 030024；3.山东省科学院 海洋仪器研究所,山东 青岛 266001)

模糊相关机会规划(fuzzy dependent-chance programming,FDCP )[1-2]，属于不确定规划中的模糊规划的子类之一，针对的是决策者在模糊环境中为了极大化模糊事件成立的机会，从而提供最优选择的一类规划。长久以来，如何能对这类模型问题进行高效求解是普遍存在于管理、工程应用、优化算法研究等领域中的热点问题。

在最优控制、电力调度等实际应用领域里，这类问题的提取很轻松，可因其具有模糊性和非线性等特点使得对它的求解或者计算并非易事，因此，进一步研究这类问题的高效求解方法很有必要。目前，智能计算有了快速发展的计算机技术平台的支持，已经可以求解常规的、传统的方法不易计算的复杂优化问题，在各个应用领域也发挥了突出效果。通过文献可知，这类模型问题主要是利用进化策略(evolution strategies)、遗传算法(genetic algorithm,GA)以及差分进化算法(differential evolution algorithm,DE)等智能计算技术和模糊模拟技术相结合求解的。大量的文献表明遗传算法[1-7]在智能算法中应用得最成熟、效果最好且最广泛，但因GA存在着遗传操作过程复杂以及计算量大、控制变量较多、耗时长等固有不足，更高效地求解或计算这类模型问题依旧是学者们的努力方向。

在真实环境中蜜蜂的自组织觅食行为启示下，人工蜂群算法(artificial bee colony,ABC)算法应运而生。它是人工鱼群算法、粒子群算法及蚁群算法之后，又一个受启于群体智能的启发式智能搜索算法。2005年，ABC算法被学者D.Karaboga为了求解含有多变量的函数的优化问题而最先提出[8]，如今已是智能计算技术的一个重要组成部分，该算法具有结构简单、需要控制的参数不多、易于编程实现、鲁棒性强等特点。与粒子群、遗传算法等智能求解算法相比，在整个寻优期间中，每一次的迭代都进行了全局、局部搜索，3种类型的蜂在不同情况下进行转换，这使ABC算法找到最优解的概率大幅度提高，同时在较大程度上避免了陷入局部等显著优点。不到15年的时间，其理论在电力系统调度、图像和信号处理、机器人行为调控、最优路径选择等众多应用领域得到应用[9-20]。从查阅的文献可知，目前尚无ABC算法在模糊规划问题求解中的报道。本文是把ABC算法与模糊模拟技术结合起来求解模糊规划中的一个子类：模糊相关机会规划模型问题，ABC算法的实效性通过经典的算例得到检验，实现了ABC算法对这一子类问题的高效求解；此外，它也为模糊机会约束规划、模糊期望值规划模型以及其他的不确定规划问题的求解提供了思路。

1 模型描述

FDCP单目标数学模型一般可以表示为以下形式

(1)

式中：C表示可信性测度;ξ和x分别表示模糊向量和决策向量；模糊不等式组{hk(x,ξ)≤0,(k=1,2,…,q)}刻画的是模糊目标事件；不确定环境用{gj(x,ξ)≤0,(j=1,2,…,p)}来表征。整个模型表达了在模糊不确定环境中使模糊目标事件的可信性最大化。在模糊不确定环境下，模糊事件的机会等于与该事件相容的可能性、可信性或必要性，这是计算FDCP模型问题的不确定原理。

在相关机会规划中，若预先给定了优先结构和管理目标，则可极小化与该目标的正或负偏差值，得到相应的目标规划数学模型

(2)

式中：gj表示模糊环境中的约束函数；Pj代表优先级权重，表示各管理目标的相对重要程度，而且，对于∀j,有Pj≫Pj+1；第i个目标高于、低于相对应的目标值的偏差分别用di+、di-表示；系统约束、目标约束的数目分别用p和m表示；bi代表第i个目标的函数值；l代表优先级的数目；hik表示目标约束中的实值函数；用uij与vij分别代表约束中的第i个目标、优先级为j的正与负偏差值的权重系数。

2 人工蜂群算法

人工蜂群算法是一种经典的仿生群体智能寻优计算方法，它源于自然界中蜜蜂的群体自组织觅食：蜜蜂可按照各自的角色或分工，通过气味、舞蹈动作等多种信息交流方式，使得蜂群总能有效地找到花蜜量最大的蜜源。该算法就是通过模拟蜜蜂寻找最大量蜜源的这个过程实现寻优。

在ABC算法模型中划分了采蜜蜂、侦察蜂、观察蜂这样3种类型的蜜蜂。采蜜蜂同正在采集的蜜源一一对应，其数量是蜂群总数的一半，而每个蜜源的所在位置代表了待优化问题的潜在解；通过跳摇摆舞等方式，采蜜蜂与其他蜜蜂共享蜜源信息，采蜜蜂总能记得它们之前的最优位置，并根据自己的记忆在邻域中进行搜索；观察蜂在舞蹈区等待，它们通过分享来自采蜜蜂提供的信息对蜜源再进行选择，其数量等于采蜜蜂的数量，在算法中主要用于提高算法的收敛速度；而那些放弃了蜜源的采蜜蜂则变成了侦察蜂，其任务就是在蜂房附近开始随机地搜索一个新的蜜源，起到了摆脱使算法陷入局部最优的作用。

设蜜源的总数为Ns，蜜源位置代表了待求优化问题的可能解向量，待求解问题的维数用D表示。在人工蜂群算法中，优化问题的求解过程实质上就是在给定的D维问题空间中搜寻最优解的过程。设蜜源i在第n次迭代时的位置用Xi=[xi1,xi2,…,xiD]表示，依据(3)式，在问题空间随机产生蜜源i的初始位置

(3)

依据(4)式，采蜜蜂在邻域中进行搜索新的蜜源

(4)

(5)

式中：pi代表第i个观察蜂的跟随概率;fi代表适应度值;Ns代表蜜源数目。

以求解最小值问题为例，解的适应度值fi按照(6)式进行计算

(6)

式中：fi、vi分别表示第i个解的函数适应度值、函数值。

(7)

在所有的采蜜蜂和观察蜂结束整个搜索空间的搜索后，若蜜源的适应值经过Ntest次到达了给定的值Nlimit后(Nlimit表示放弃该蜜源的阈值)依旧没有得到更好的蜜源时，表示该解已经陷入了局部最优。那么，fi所对应的蜜源被放弃，而与该蜜源所对应的采蜜蜂也就转变成了侦察蜂。依据(7)式，该侦察蜂随机地产生一个新的位置，一旦新的蜜源找到了，它又转变为采蜜蜂。

所以，ABC算法的核心点在于：采蜜蜂搜寻蜜源；依据采蜜蜂所提供的花蜜量信息，观察蜂以一定的选择概率再去选择蜜源；若某个蜜源被采蜜蜂和观察蜂所耗尽，则变成侦察蜂，重新随机生成一个新的位置。

3 求解FDCP模型问题的人工蜂群算法

求解FDCP问题时要通过人工蜂群算法完成寻找最优解，在整个寻优过程中，算法需要解决模糊适应度值的计算问题。适应度值的求解与模糊机会函数即模糊事件的可信性值(或者可能性、必要性)的求解紧密联系。对于模糊机会函数值的计算，若用常规的解析方法很难实现。而模糊模拟技术是在模糊系统中进行抽样的一种技术，它在多维模糊变量问题中已经广泛使用，模糊机会函数值通过模糊模拟技术可以很方便地进行求解。在利用人工蜂群算法进行寻优期间，它主要表现在：初始化阶段，要用模糊 模拟 来实现所有蜜源的机会函数值的计算；在每一次迭代时，也需要通过模糊模拟求解蜜源的机会函数值等。

3.1 模糊模拟算法

常规的解析法很难计算可信性测度，通过模糊模拟技术求解模糊事件的可信性：L=C{f(ξ)≤0}。

下面给出模糊模拟可信性估计算法的流程：

第1步θk从非空集合θ中均匀生成后使得它能满足条件Pos{θk}≥ε,其中的k=1,2,…,N;同时定义vk= Pos{θk},这里的k=1,2,…,N;ε代表一个充分小的数。

第2步计算如下式子

第3步返回计算结果L。

3.2 算法流程

求解FDCP问题的人工蜂群算法的具体流程如下：

第1步首先，对于NP个蜜源xi(i=1,2,…,NP)，在D维空间上先初始化：采蜜蜂的数目等于观察蜂的数目等于蜜源总数据的一半，在蜜源停留的最大限制次数Nlimit,算法的最大迭代次数Nmaxcycle,各个维度的上界及下界值，随机生成NP个初始蜜源，可通过(3)式计算每个蜜源的花蜜量即适应度值，也就是通过模糊模拟可信性 估计算法来计算模糊机会函数值；对观察蜂也要进行初始位置等相应的初始化工作以及对最优蜜源的初始位置、花蜜量等进行初始化等。

第3步通过(5)式，计算采蜜蜂找到蜜源被观察蜂跟随的概率，观察蜂根据该概率的大小选择蜜源。

第4步观察蜂搜寻蜜源(与采蜜蜂相同的方式)，通过上面描述的模糊模拟算法计算机会函数值、适应度值，即蜜源的花蜜量，依据贪婪选择策略，保留当前的最优蜜源。

第5步为增加蜂群的多样性，检测各蜜源是否达到了被放弃的阈值，即检测各蜜源的持续搜索次数记录变量Ntest是否到达Nlimit，若超过，则通过(7)式随机生成一个新的食物源来代替旧食物源，通过上面描述的模糊模拟算法计算模糊机会函数值、适应度值，相应的采蜜蜂变为侦察蜂，依据贪婪选择策略，保留当前的最优蜜源。

第6步结束条件判断：检查算法是否达到预先给定的停止准则(给定的计算精度或Nmaxcycle),若满足，则转向第7步，否则转向第2步。

第7步停止计算，给出最优值及相对应的解。

4 仿真测试和实验结果分析

采用算例[1]开展仿真实验以验证本文ABC算法的效果。

例1计算以下的单目标模型问题

例2求解以下的模糊相关机会规划的目标规划问题

对于例1,事件为：x12+x22+x32=1用ε表示，它的支撑ε*={x1,x2,x3}，它的相关支撑ε**={x1,x2,x3}，依据不确定原理可得到事件ε的模糊机会函数f(x)的值通过下式计算

机会函数的值可用模糊模拟技术计算得到。

算法代码中参数的取值和文献[1]相同。模糊模拟总次数：5 000；种群数量：30；迭代次数：400；运行次数：1。此外，观察蜂的数量等于采蜜蜂的数量(等于15)，阈值Nlimit=15。

对于例2，第一优先级里的事件为x1+x32=3，用ε1表示， 它的支撑为ε1*={x1,x3}，它的相关支撑为ε1**={x1,x2,x3,x4}。依据不确定原理可得到该事件ε1的机会函数f1(x)为

类似地，第二优先级里的事件为x2+x52=2，它的机会函数f2(x)为

第三优先级里的事件为x4+x62=1，它的机会函数f3(x)为

显然这3个机会函数的值可以通过模糊模拟技术计算得到。

程序代码参数的取值和文献[1]相同。模糊模拟总次数： 5 000；蜂群数量：30；观察蜂数目：15；迭代次数：400；采蜜蜂数目：15；阈值Nlimit=15。

本文的ABC算法通过Visual C++6.0编程，在inter(R) coreTMi5-7400cpu@3.00 GHz、8 GB内存、win10的计算机上运行。

在例1中，ABC算法执行一次后的最优解和最优值见表1，与文献[1]中的求解结果相对比，文献[1]的计算优势远远不如本文算法的优化结果。如图1的迭代过程抽样分析，展现了本文所提出的人工蜂群算法的整个迭代过程，我们把代码执行的迭代流程进行了80次的数据采样。人工蜂群算法求解精度高、收敛速度快，文献[1]中，GA算法进行了400次的迭代后所求得的最优结果，在本文的基于ABC的算法中15次迭代以内就可以达到；而且，从该迭代过程抽样分析图中可以看到，随着搜索的不断进行，待求问题的最大值也趋于稳定，该求解算法的稳定收敛性无需多言。另外，将该程序代码执行10次后进行最终求解结果对比，每一次所得的运行效果类似，而且全局最优值平均从第9次迭代就超过了文献[1]在400迭代时的全局最优值，平均最优解和最优值见表1。

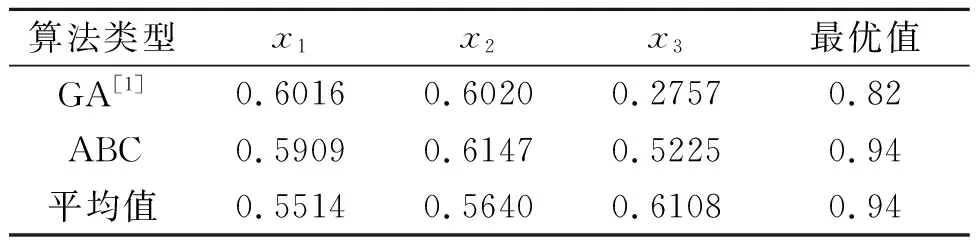
表1 实例1中不同算法的优化结果对比Table 1 Comparison of optimization results of two algorithms in case 1

表2 实例2中不同算法的优化结果对比Table 2 Comparison of optimization results of two algorithms in case 2

5 结 语

本文研究了ABC算法与模糊模拟技术相结合，即将模糊模拟技术嵌入到ABC算法中求解相关机会规划的求解算法问题，通过与以GA智能算法为核心的求解算法的实例仿真的结果对比，验证了基于人工蜂群算法的方法在求解质量和收敛速度及稳定性方面效果明显，能够很好地解决这类优化问题的计算，展现了其在该类问题上的算法的优越性，在连续空间的相关机会规划问题进行高效计算。本文所提出的方法是一种全新的方法，具有潜在的应用价值， 填补了ABC算法在模糊规划问题中应用研究的空白，而且也拓宽了ABC算法的应用研究领域。

值得说明的是，本文作者将ABC算法也对其他2种模糊规划和随机规划问题进行了求解，得到了和本文类似的求解效果，它对其他的双重不确定规划模型问题的计算方法有借鉴意义，也是我们后继要开展的研究工作。