基于改进IMM算法的机场移动目标轨迹跟踪与预测*
赵文杰 汤新民* 黄忠涛 朱 盼
(南京航空航天大学民航学院1) 南京 211100) (中国民航局第二研究所2) 成都 610041)
0 引 言
目前,国内外先进的民航机场的场面监视,主要是通过场面监视雷达(SMR)实现的[1-2].但SMR容易受到外界因素的影响,抗干扰能力比较差.本文航空器监视数据是利用机载的ADS-B设备获取的.由于ADS-B技术依赖GNSS系统(全球导航卫星系统)对目标进行定位[3].因此,ADS-B技术本身缺乏对目标真实位置的验证功能[4].要得到尽量接近真实值的定位信息就需要运用交互式多模型对位置和速度方面进行误差修正.
IMM算法在各种目标跟踪问题中非常有效,使用有限数量的不同模型来描述目标的行为,并且不同模型之间的相互作用由转移概率矩阵控制[5-6].目前国内外一些学者对IMM算法进行了改进,戴定成等[7]通过重新定义模型误差压缩率之比,提出了一种改进的马尔可夫参数自适应IMM算法.封普文等[8]基于后验信息修正,扩展了一种在线更新马尔可夫概率转移矩阵的自适应跟踪算法.Samuel等[9]提出了一种改善混合系统噪声的高机动目标跟踪滤波器性能的方法,设计了有色噪声一阶离散马尔可夫系统.通过使用具有离散白噪声加速度和水平协调转弯模型的IMM滤波器来完成跟踪.以上学者仅对算法做了跟踪过程的马尔可夫参数的改进,并没有将改进的算法应用到目标轨迹的预测过程,当缺少观测值时算法失效.刘恒泽等[10]提出了运用IMM对目标进行跟踪时的航迹外推算法能够在进行记忆跟踪的时候保持目标的运动趋势,但是没有结合实际运动情况,所以在预测时会产生一定的误差.
本文旨在通过ADS-B获取机场航空器/车辆位置信息,通过改进的轨迹外推算法结合机场统计的移动目标路径选择概率对移动目标意图预测,防止车辆驾驶员和飞行员产生偏差.
利用IMM做外推的不足,必须结合先验信息,如何将先验信息修正当前状态转移矩阵.
1 机场场面信息及建模
1.1 坐标转换
由于ADS-B接收到的位置信息为经纬度信息,所以需要先将经纬度信息转换成以机场某一点为原点的平面直角坐标系.
ADS-B报文中目标位置的表示是采用椭球坐标系(φ,λ,h).其中:φ为纬度;λ为经度;h为飞行高度.经过坐标变换到地心直角坐标系(x,y,z),其坐标转换公式为
(1)
式中:a为地球的长轴半径(6 378 137 m);b为地球的短轴半径(6 356 752 m).设本地中心点的大地坐标经度、纬度、高度为(φ′,λ′,h′),根据上述转换公式,得本地中心点在地心直角坐标系中的位置为
(2)
WGS84坐标系下目标在本地直角坐标系中的坐标为
(3)
RT为旋转矩阵
(4)
经过坐标转换,可以将机场中任一点表示为相对于ADS-B地面站为原点的坐标,将跑道和滑行道等活动区域进行划分,并可以用坐标表示出来该区域的范围.
1.2 路网及先验信息建模
1) 路网建模 本文以禄口机场为背景,见图1.从机场交通路网的实际结构出发用图来表示其连接关系,见图2.图中的节点抽象为机场中道路与道路之间的交叉点,边抽象为两个交叉点之间连接的路段,两个相邻节点之间的概率作为选择该路段的量化属性,从而对跑道及滑行道进行路网建模.机场中的道路交叉口用节点表示,交叉口之间的路段用边表示.路网模型为G=(V,E,X).其中:V={na,a=1,2,…,9}为节点集合;E={Lb,b=1,2,…,10}为边的集合;X={(xa,ya)}为第a个节点机场位置的物理坐标.

图1 禄口机场部分场面地图

图2 禄口机场路网模型
2) 构建概率邻接矩阵 由机场统计的ADS-B历史数据可得每个节点之间的转换概率并可得到概率邻接矩阵.通过预计的下一节点与该节点的坐标差值(xa+1-xa,ya+1-ya)和当前航向比较,如果两点连线的矢量和速度矢量的夹角在很小的范围内认为是直行,否则转弯,进而可以得到某节点预计转弯和直行的概率.
由图2可知,共有9个结点的图G=(V,E,X),最简单的方法是使用一个n×n阶的概率矩阵A=(aij)n×n来定义,其中:
(5)
式中:1为连通;dij为机场中先验信息节点i向节点j的路径转换概率.
则该图的概率邻接矩阵可以表示为
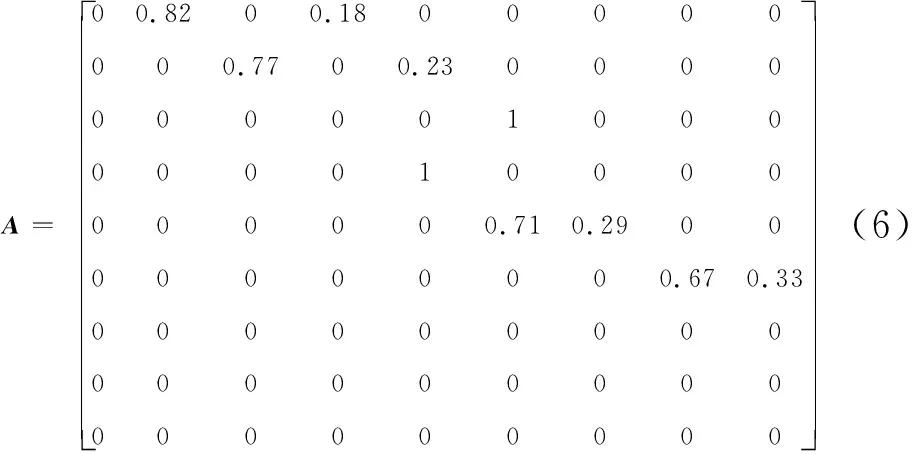
1.3 路段速度建模
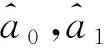
(7)
转换成矩阵为
(8)
对路网中每一条路段的移动目标速度进行统计,统计在路段Lb(b=1,2,…,10)的匀速运动与匀变速运动的概率由矩阵B表示
2 基于交互式多模型的跟踪和外推
根据机场模型对机场进行坐标转换,结合移动目标轨迹统计数据与实时处理的ADS-B数据,选取需要跟踪或预测的移动目标.然后判断目标的运动过程是否有可靠的观测值,如果存在可靠的观测值,则通过当前的观测值结合传统的IMM算法对其进行轨迹跟踪;否则,利用根据历史信息结合修正的IMM轨迹外推算法对其轨迹进行预测,具体过程见图3.
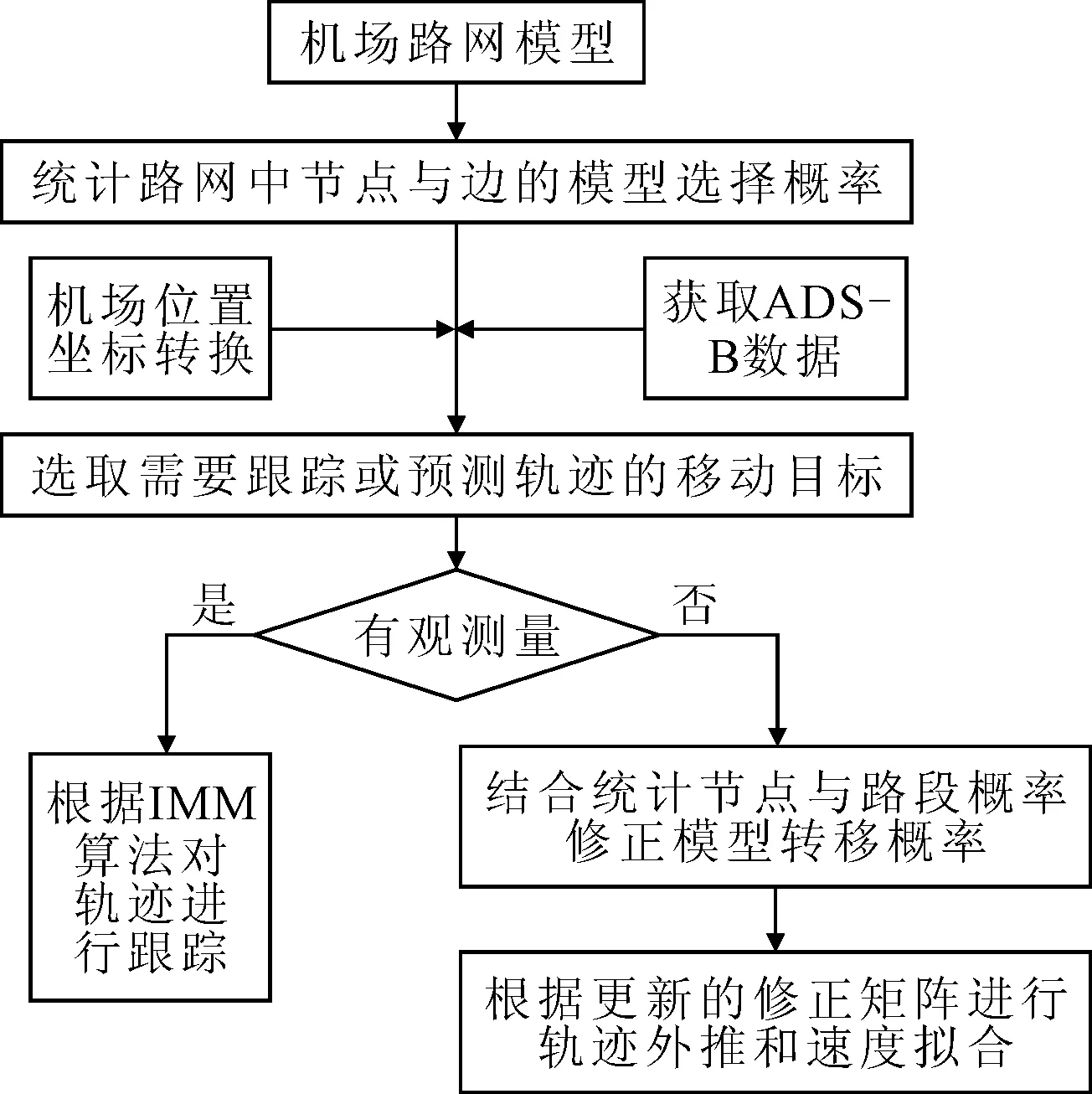
图3 基于IMM轨迹跟踪与外推过程
2.1 IMM算法
为了描述运动目标的运动状态,将对各种运动状态进行数学模型建模,分别用运动目标的运动状态模型与量测模型表示.
状态方程:
X(k)=F(k-1)X(k-1)+G(k-1)W(k-1)
(9)
观测方程:
Z(K)=hX(k)+v(k)
(10)
式中:X(k)∈Rn为状态向量;F(k)为n维系统状态转移矩阵;G(k)为噪声驱动矩阵;W(k)为状态方程白噪声;v(k)量测噪声向量;Z(K)∈Rm为量测向量.
飞机在机场场面运动一般有三种运动模式,分别为匀速直线运动模型(CV),匀变速直线模型(CA),匀速转弯模型(CT).在每一条路段(跑到、滑行道)中主要包括CV与CA模型,在路段与路段的交叉口处主要包括CT模型.
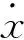
运动学公式可表示为
(11)

X(K)=FCV(k-1)X(K-1)+
GCV(k-1)WCV(k-1)
(12)
即
(13)
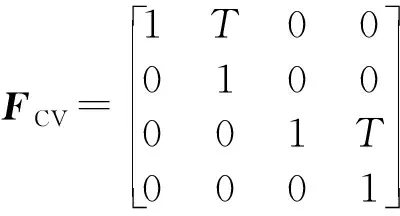
系统观测转移矩阵:


X(K)=FCT(k-1)X(K-1)+
GCT(k-1)WCT(k-1)
(14)
(15)
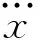
X(K)=FCA(k-1)X(K-1)+
GCA(k-1)WCA(k-1)
(16)
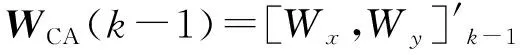
交互式多模型算法引入多个目标运动模型,具有自适应的特点,能够有效地对各个模型的概率进行调整,并按照相应的概率对每个模型的状态估计进行加权,实现对运动目标的跟踪,在实际应用中,产生良好的效果.IMM滤波算法主要包括四个步骤,分别为输入交互、并行滤波、模型概率更新和输出数据融合.
输入交互概率:
(17)
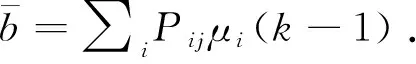
由文献[11]知IMM算法的并行滤波过程采用的是卡尔曼滤波,此处不再赘述.
似然函数:
(18)
(19)
输出数据融合:
(20)
2.2 修正马尔科夫矩阵的轨迹外推算法
在IMM算法中,输入的交互过程一般为马尔科夫过程,而模型初始转移概率由人为确定,并不会随着实际运动情况而变化.当目标实际运动与初始转移概率的偏差较大时,这种人为确定的Markov矩阵会因为情况的变化失真而不能准确反映目标的实际运动模式转换情况,鉴于此,本文利用机场中跑道与滑行道运行的概率等先验信息对其进行实时修正,使之切合目标实际运动状态.

(22)
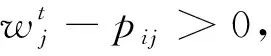
考虑到某时刻某一模型向所有的模型转移概率之和应为1.因此,需要对上式进行归一化.修正后的转移概率计算公式为
(23)
由式(23)可知,当其他模型向模型j转移的概率增大时,修正后的Markov矩阵中的第j列元素也会随之增大,那么在下一时刻的模型交互中,机场先验信息模型概率大的子模型将占据更大比重;相反,机场先验信息模型概率小的子模型所占的比重将减小.
利用该比值对概率矩阵进行修正,得
(24)
在通常情况下,当k时刻没有获得符合条件的观测值时,需要进行轨迹外推.单一模型情况下通过卡尔曼滤波建立目标轨迹模型,可以通过式(24)得到状态值的一步预测值进行轨迹外推.
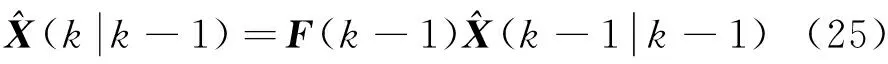
式中:F(k-1)为状态转移矩阵.在交互多模型的情况下,由于目标模型是通过多个模型相互作用得到的,因此无法获得确定的F(k-1),无法运用式(25)进行轨迹外推.k时刻初始条件Xoj(k-1|k-1)和Poj(k-1|k-1)的计算不受观测向量的影响,因此在k时刻没有可信观测信息时,可以通过式(25)和式(26)分别计算出各模型的状态预测值和预测协方差矩阵.对模型j进行外推过程如下.
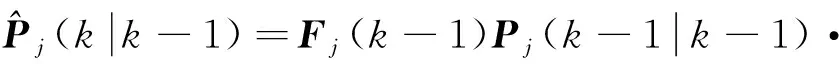
式中:G(k-1)为第j个模型的过程噪声传递矩阵;Qj为噪声协方差矩阵;T为采样周期.其中Fj(k-1)和G(k-1)可由CA,CV,CT模型分别得到.
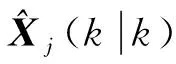
(28)
(29)
(30)
由式(30)可得的状态预测值和预测滤波均方误差阵建立目标的外推轨迹,从而实现了交互式多模算法的场面飞机与车辆的轨迹预测.
3 仿真实验与分析
飞机落地时初始位置为(0,0),在跑道上先经过一段匀变速运动接着在跑道中匀速运动,到达图2中的n2节点时转弯再经过一段匀速过程到达n5节点,在此之前为跟踪过程,从n5节点之后进行轨迹的外推,其中采样周期为1 s.其中,初始模型概率为μ=[0.3,0.3,0.4],初始马尔科夫转移概率为Pij=[0.9,0.05,0.05;0.05,0.9,0.05;0.05,0.05,0.9],观测噪声协方差为R=diag{[20,20]},过程噪声协方差矩阵Q=diag{[10,10]}.
在观测数据正常的情况下,运用交互式多模型算法进行目标跟踪,当没有符合要求的观测数据时,运用外推算法进行轨迹外推,轨迹的外推见图4.

图4 外推轨迹
为了验证修正马尔科夫矩阵的轨迹外推算法与未修正的外推算法的预测效果,分别对两种算法进行仿真实验,其中“预测一”表示修正马尔科夫矩阵的轨迹外推算法的预测轨迹,“预测二”表示未修正的轨迹外推算法的预测轨迹.仿真结果见图5.轨迹外推的次数与比例见表1.

图5 外推算法预测轨迹

表1 轨迹外推的次数与比例
为了进一步验证两种算法在轨迹选择上都预测正确的前提下,速度误差的大小,本文选取了图5a)情况下运用最小二乘法进行拟合并对速度误差进行仿真,仿真结果见图6.其中“V-1”为改进的轨迹外推算法的速度随时间变化曲线,“V-2”表示未改进的轨迹外推算法的速度随时间变化曲线.由图7可知,曲线“V-1”较曲线“V-2”更接近真实曲线,说明改进的外推算法对速度的拟合比未改进的外推算法效果要好.

图6 外推算法速度曲线
图7为两种外推算法速度误差曲线,均值与方差见表2,改进的外推算法速度误差在平均值与方差上都更接近真实值,因此速度的拟合效果更好.
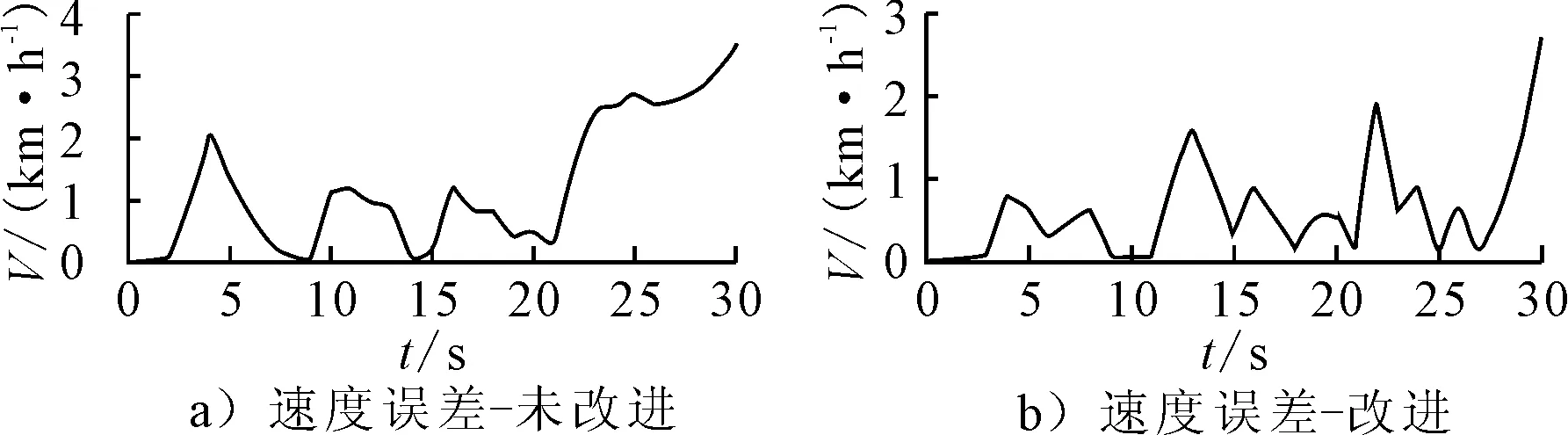
图7 外推算法速度误差曲线

表2 两种外推算法速度误差对比
本文通过设计仿真实验验证了改进的轨迹外推算法在移动目标缺少观测量时根据已有的信息对其轨道选择准确率比未改进算法有明显提高,当两种算法同时对轨道选择预测准确的情况下,改进的轨迹外推算法对于速度的拟合效果更好,因此能够对目标状态进行较好的预测.
4 结 束 语
本文根据机场路网信息和移动目标的运动模型,实现了对目标进行轨迹跟踪,在此基础上提出了IMM轨迹外推算法当缺少可靠度观测值时结合历史统计数据根据外推算法进行轨迹的预测.将过去时刻的历史信息融入到马尔科夫状态转移概率矩阵中,在移动目标每经过一个节点马尔科夫矩阵就会自动更新,使其更符合真实的目标运动状况,从而使滤波器更好地适应目标运动状态的变化,以获得更佳的目标轨迹预测效果.仿真结果进一步证明了改进的IMM外推算法比未修改的轨迹外推算法准确度更高.

