FLAC3D 中Cable 数量对锚杆拉拔模拟试验结果的影响

杜学领

（贵州理工学院 矿业工程学院，贵州 贵阳550003）

锚杆是支护工程中的主要材料之一，近年来，D锚杆、恒阻大变形锚杆、中空注浆锚杆等新型锚杆的研发、锚杆监测技术的进步及支护理论的深入研究[1-5]，进一步提升了锚杆种类的丰富性和支护设计的科学性。FLAC3D是岩土、矿业领域被广泛应用的数值模拟软件之一，断层影响、冲击地压评价及支护系统特性等问题均可在FLAC3D中进行研究[6-10]。但在FLAC3D中，依托Cable 建立锚杆的模拟效果与其数量有关。不同的Cable 数量，可能影响到模拟的准确性。尽管Itasca 公司提出了2 条建议[11]：“1. Try to provide approximately one node in each FLAC3Dzone.The reasoning here is that since the zones are constant-stress regions, it is not necessary to have more than one interaction point within a zone; 2. Try to provide two to three cable element within the development length of the cable. The “development length of the cable is determined by dividing the specified yield strength, Ft, by the grout cohesive strength, cg. By following this procedure, failure by“pull-out”can occur if such conditions arise. If the cable elements are too long, then only the yield failure mode of each element is possible”，上述建议同样适用于使用Pile 结构单元建立岩石锚杆的情况。但在已有文献中，一些研究并没有应用上述原则或者未提及数值模拟中Cable 的数量问题，例如李为腾等在拉拔模拟和支护模拟中分别设定单个Cable 长度为0.05、0.1 m，但其并未指明Cable 密度与围岩网格尺寸的关系[12]；刘少虹对单个Cable 长度的设定为0.11 m，其Cable与围岩为非均匀接触，非均匀条件下的锚杆受力是否存在尺寸效应仍需要进一步评价[13]；黄庆享等对软岩大变形巷道支护方案的模拟中，并没有给出数值模拟中锚杆所采用的物理参数和设置方案[14]；类似的未给出数值模拟中锚杆设置详情的研究还大量存在[15-17]，以至于降低了数值模拟的可信度和可重复性。尺寸效应广泛存在于PFC、UDEC 等数值模拟及物理实验中，并已有大量尺寸效应报道[18-21]。但FLAC3D中Cable 数量与围岩网格的匹配性问题，尚未引起足够重视。对于煤矿巷道支护工程而言，顶板、帮部的锚杆长度一般为1.6～2.4 m 左右，与边长为30～50 m 的数值模拟研究模型相比，Cable 数量是否影响锚杆性能还需要进一步评价。在固定网格尺寸、锚杆长度的情况下，通过在拉拔试验中改变Cable 的数量，评价FLAC3D中不同Cable数量对模拟结果的影响。

1 研究方案

借鉴已有研究成果，在FLAC3D中利用Cable 结构单元建立锚杆模型，模型尺寸及测点布置如图1。

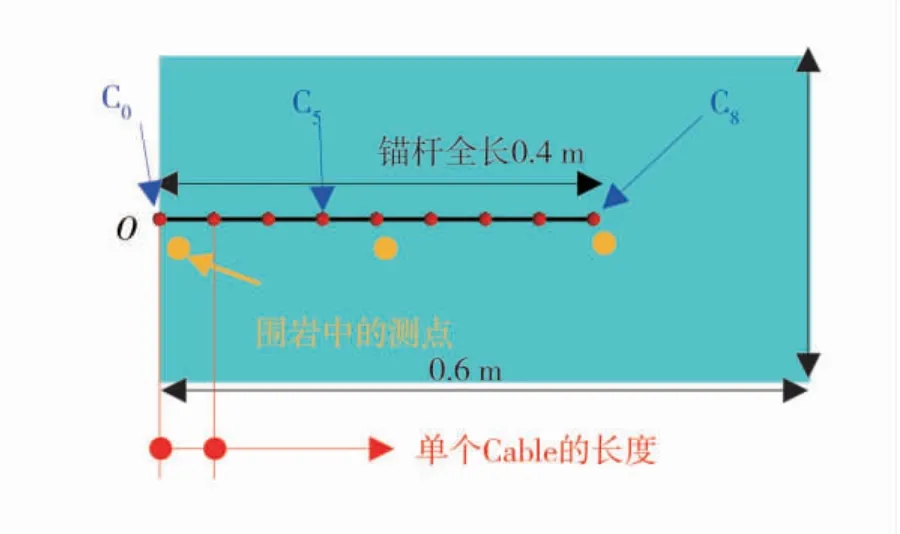
图1 模型尺寸及测点布置示意图Fig.1 Schematic diagram of model size and position of the measurement points

锚杆长度为0.4 m，起点及拉拔端均位于坐标原点O 处。围岩尺寸为x×y×z=宽×长×高=0.3 m×0.6 m×0.3 m，围岩网格密度为0.01 m 1 个网格。围岩采用应变软化模型，其参数与文献[22]中表1、表2 中所采用的煤的参数相同；锚杆采用全长锚固，Cable 的参数与文献[22]中表3、表5 中的参数相同。文献[22]未提及的grout-perimeter、grout-stiffness，本文分别设定为0.094 2 m、28 GPa。与文献[22]有所不同的是，本文仅研究Cable 数量对模拟结果的影响，因此不对锚杆施加预紧力，且由于锚杆长度、模型尺寸及网格划分与文献[22]有所不同，本文采用的拉拔速度为10-6m/step，所有模型均运行10 000步以便于对比模拟结果。拉拔结束时，拉拔端的结点（node）位移为10 mm，根据物理拉拔试验中，常规的锚杆在此位移下已达到峰值载荷并已进入峰后阶段[23-24]。模型的边界条件与FLAC3D手册中的案例“Simulation of Pull-Tests for Fully Bonded Rock Reinforcement”使用Cable 建立锚杆的边界条件相同，且不考虑密度及重力的影响[11]。沿锚杆轴向每隔0.05 m 布置1 个测点监测拉拔过程中的锚杆轴力演化，并分别编号为C0、C1、…、C8。在z=0 平面，在x=y=0.01 m 处开始沿y 轴间隔0.2 m 布置3 个测点监测拉拔过程中围岩中的应力响应，此3 个测点可反映锚杆两端及中部所引用的围岩应力变化。

根据文献[22]的参数及文献[11]的建议，本文的研究条件下锚杆的development length 为0.133 m，该长度上应有2～3 个Cable，即：约0.04 m 1 个Cable。但文献[11]同时提出，应对1 个zone 提供接近1个而无需过多的结点，围岩网格密度为0.01 m 1 个网格，按此计算则约0.01 m 1 个Cable。二者存在一定矛盾性，这种矛盾也会因研究问题的差异而出现在不同的数值模拟中。为了研究Cable 数量对模拟结果，本文以0.04 m 1 个Cable 为基准，并标记为“标准组”；分别以0.02、0.01、0.005 m 1 个Cable 为基准建立加密的Cable 研究方案；分别以0.05、0.08、0.1、0.2 m 1 个Cable 为基准建立相对疏松的Cable研究方案，此时部分轴力测点的数据完全相同，在后续分析中仅选取部分测点用于说明问题。

2 数值模拟结果及分析

2.1 拉拔端的轴力-时步演化特征

对于拉拔试验而言，常规锚杆的轴力沿拉拔反方向快速衰减，最大轴力出现在拉拔端附近[1]，因此，拉拔端的轴力在一定程度上能反映锚杆在拉拔过程中的特性。不同Cable 数量时锚杆拉拔端轴力-时步演化过程如图2，由图2 可知，尽管围岩属性、网格密度、边界条件、锚杆长度等条件均相同，但对相同长度锚杆划分为不同Cable 数量时，模拟结果有明显不同。Cable 数量与单元网格密度具有重要相关性，当单一Cable 长度与网格长度划分一致或比网格更短时，锚杆能获得较大的拉拔轴力，如0.01 m 1 个Cable 时（单一Cable 长度与网格长度划分一致）锚杆最大轴力可达到114 kN，0.005 m 1 个Cable 时（单一Cable 长度是网格长度的2 倍）锚杆最大轴力可达到锚杆的抗拉强度266 kN；而当单一Cable 长度低于网格长度时，锚杆拉拔端最大轴力要低于50 kN，该数值远小于锚杆的抗拉强度，说明此时锚杆并没有发挥出高承载的性能。由于不同的锚固条件下所获得的锚固效果是不同的，可以根据现场的拉拔试验确定锚杆的极限拉拔力，然后在数值模拟中设定单一Cable 长度为网格长度的0.5～1 倍之间，寻找与现场试验相符合的模拟方案。

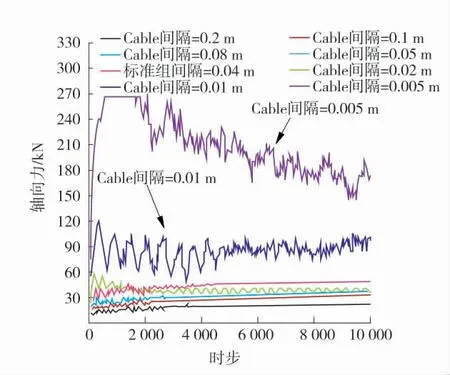
图2 锚杆拉拔端轴力-时步演化过程图Fig.2 Evolution of axial force at the pull-out end and step

2.2 拉拔引起的围岩应力演化

不同模拟方案中围岩不同位置沿拉拔方向的应力演化过程如图3。

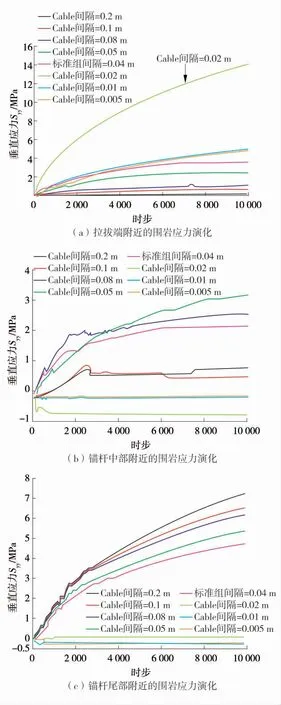
图3 围岩不同位置沿拉拔方向的应力演化过程Fig.3 Stress evolution of different positions of surrounding rocks along the pulling direction

从图3 可知，因对相同长度的锚杆设置不同的Cable 数量，导致围岩中的应力演化也会出现较大差异。当1 个Cable 的长度显著大于网格长度时（1 个Cable 长度在0.05～0.5 m 时），造成拉拔端附近的围岩应力较低（图3（a）），而锚杆尾部的应力则相对较大（图3（c）），这种情况与物理实验是不符合的。在物理实验中，锚杆尾部的轴力较小，因此其引起的附加应力场也相对较小，从这个意义而言，对于相同长度的锚杆，当Cable 数量较少时，无法正确反映出锚杆与围岩的相互作用。在单纯拉拔条件下，锚杆中部附近的围岩应力变化应体现出从拉拔端到锚杆尾部的渐变特性，其数量级一般应低于拉拔端附近的应力量级，由此观之，图3（b）中1 个Cable 长度为0.04 时的情况也与物理实验不符。

对上述不合理方案进一步检视发现，当Cable的数量较少时，围岩中的应力呈现出分散性分布的特点，标准组方案中围岩应力分布图如图4，Cable数量少于标准组时，其围岩中的应力分布均与此类似。由图4 可知，当Cable 数量较少时，围岩中的高应力以靠近结点所在位置为中心，而与拉拔位置关系不大。这显然并不符合常规全长锚固锚杆的拉拔特性。这不仅说明Cable 数量较少时所表征的工程问题极有可能是错误的，还说明按照FLAC3D帮助手册中根据development length 设置Cable 数量的建议也是不可靠的。

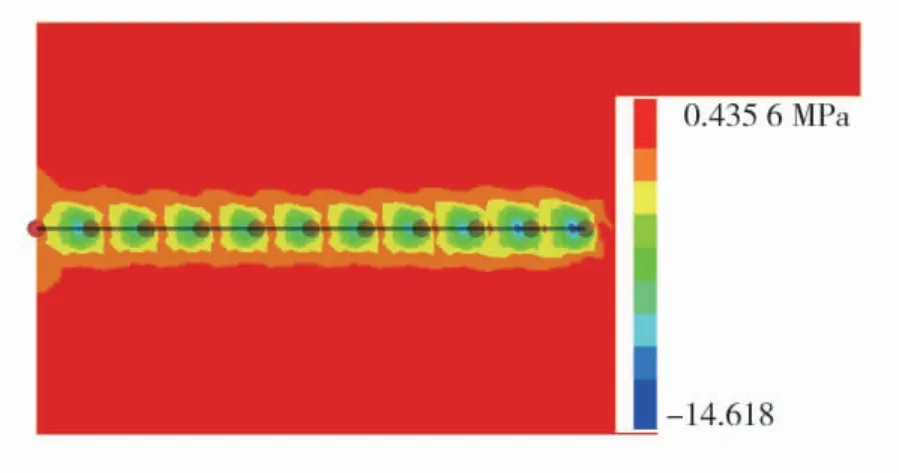
图4 标准组方案围岩中分散性应力分布Fig.4 Dispersion stress distribution in surrounding rock of the standard group

3 数值模拟讨论

3.1 单位长度锚固剂刚度问题

前述研究设定单位长度锚固剂刚度grout-stiffness（以下简称“锚固剂刚度”）为28 GPa，由于文献[22]并未明确给出锚固剂刚度的数值，本文分别设定锚固剂刚度为5、10、15、20、35、40 GPa，以单一Cable 长度与网格尺寸相一致的模型为基础，进一步观察模拟结果的差异。不同锚固剂刚度时的轴力-时步演化图如图5。

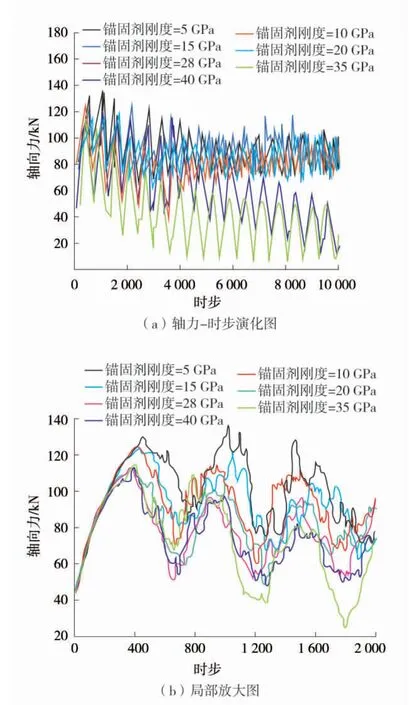
图5 不同锚固剂刚度时的轴力-时步演化图Fig.5 Axial force-step evolution with different grout-stiffness

由图5 可知，在本文的研究条件下，锚固剂刚度在5～40 GPa 之间变化时，虽然锚杆轴力随着拉拔时步的演化不尽相同，但从轴力的峰值而言锚固剂刚度变化的影响并不显著，峰值轴力约在110～130 kN 之间变化，与Cable 数量的改变相比，该变化幅值对锚杆峰值轴力的影响是相对较小的。这也说明，尽管本文指定了锚固剂刚度为28 GPa，但其对峰值轴力的分析是相对可靠的。但锚固剂刚度改变后，会改变轴力的峰后变化特征。在本文的研究条件下，锚固剂刚度低于35 GPa 时，锚杆峰后轴力波动趋稳，而锚固剂刚度不小于35 GPa 时，锚杆峰后轴力波动下降。

3.2 围岩软化特性对模拟结果的影响

本文的围岩软化特性参照文献[22]设定，以前述参数为基础，对标准试样进行单轴压缩的数值模拟测试，单轴压缩模拟结果如图6。

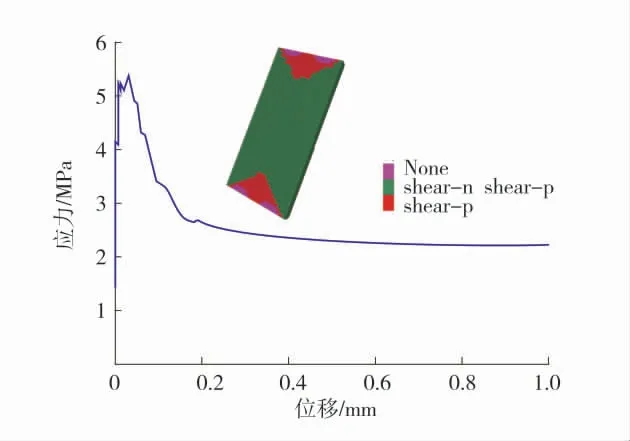
图6 单轴压缩数值模拟结果Fig.6 Numerical simulation results of uniaxial compression test

由图6 可知，数值模拟中所采用的煤的单轴抗压强度约为5.37 MPa，该数值相对于岩石而言属于软弱岩体。进一步，在模拟中受应变软化参数设置影响，煤体破坏后的强度依然保持在2.3 MPa 左右，峰后强度约为峰值强度的42.83%。在真实的物理实验中，煤岩体一般表现为脆性或塑性破坏，但破坏后的强度不会维持在较高的强度水平，而是随着位移的增加而逐渐衰减。从图6 还可以看出，围岩达到峰值载荷的位移量非常小，而在峰后则维持了较大的位移量。对于在FLAC3D中的静力学分析而言，各种物理量的叠加计算依赖于网格及其节点，由于软化后的网格依然能够承载、拉拔过程中的破坏具有非均匀演化的特点（体现在拉伸和剪切破坏有可能在不同时步发生于同一网格）等原因，就导致了拉拔模拟的轴力-时步曲线出现较为明显的波动性，这种波动性的波动幅值、波动趋势与物理实验是无法做到完全一致的。因此，尽管在数值模拟中可以通过参数校核来获得与物理实验较为吻合的结果，但实际上参数校核也只是在数值模拟中实现部分物理实验的重现，与天然煤岩体的在实验前的未知离散性表征还有一定差距。可见，在当前的技术及理论研究条件下，数值模拟完全替代物理实验而获得服务于现实的精确解是非常困难的。

3.3 数值模拟中的锚杆特性问题

文献[22]研究了利用Fish 语言实现FLAC3D中可破断锚杆的模拟问题，但从图2、图5（a）可以看出，Cable 数量、锚固剂刚度等均会对锚杆特性造成重要影响。特别是在拉拔过程中锚杆未达到极限抗拉强度的情况下，锚杆达到峰值轴力后轴力会出现衰减，此后即便发生较大的位移量锚杆也不会达到极限抗拉强度。按照文献[22]基于锚杆自由段总伸长量来进行锚杆破断判定的方法，如果数值模拟中锚杆与围岩的交互作用导致锚杆的响应本身就不合理，如图5（a），此时锚杆轴力演化本身不合理，其位移也就不具备参考价值，此时应用文献[22]的判定方法，可能也是存疑的。此外，对于锚固系统破坏时锚杆被直接拔出的情况，如软岩、矿井水影响等条件下就有可能因锚固不牢靠而发生锚杆的非破断脱锚，如何在FLAC3D中更加准确的反映出这些现象，依然需要深入研究。

4 结 论

1）对相同长度锚杆划分为不同Cable 数量时，模拟结果有明显不同。当单一Cable 长度与网格长度划分一致或比网格更短时，锚杆能获得较大的拉拔轴力，可以根据现场的拉拔试验确定锚杆的极限拉拔力，然后在数值模拟中设定单一Cable 长度为网格长度的0.5～1 倍之间，寻找与现场试验相符合的模拟方案。按照FLAC3D帮助手册中根据development length 设置Cable 数量的建议并不完全可靠。

2）从锚杆轴力的峰值而言，锚固剂刚度的变化影响并不显著，但会改变轴力的峰后变化特征。锚固剂刚度较大时，锚杆峰后轴力波动下降。

3）当前的技术及理论研究条件下，数值模拟完全替代物理实验而获得服务于现实的精确解是非常困难的。对于仅有模拟结果而缺乏模拟细节的结论，应审慎采信。