基于煤体渗透率各向异性的瓦斯抽采特性研究
张 伟,郑春山,薛 生,江丙友,王志根,刘 健,王 永
(1.安徽理工大学 深部煤矿采动响应与灾害防控国家重点实验室,安徽 淮南232001;2.安徽理工大学 能源与安全学院,安徽 淮南232001;3.中煤新集能源股份有限公司,安徽 淮南232001;4.煤矿瓦斯治理国家工程研究中心,安徽 淮南232001)
煤炭是我国的主体能源[1]。不同于浅部开采,深部的地质条件和瓦斯条件更为复杂多变,更易发生煤与瓦斯突出[2]。钻孔抽采瓦斯能够有效降低煤层的瓦斯浓度[3],减少煤与瓦斯突出事故的发生。现场确定瓦斯抽采半径的方法主要为压降法[4];梁冰等[5]通过改进传统的钻孔布置方式对压降法进行了改进,避免其他因素对瓦斯抽采效果的影响。在数值模拟方面,舒才[6]、刘三钧等[7]基于瓦斯含量建立了有效抽采半径的数学模型,并在现场得到了验证;程远平等[8]研究了抽采负压对瓦斯抽采过程的作用机理;李润之等[9-11]通过建立多物理场耦合模型,分析了瓦斯抽采过程中多种影响因素的作用,并研究了钻孔之间的相互影响,确定了合适的布孔间距;Yue G 等[12-13]使用受载煤岩瓦斯渗流试验系统对煤层各向异性渗透率进行测试,实验得出结构异性煤体的渗透率变化规律;林柏泉等[14]基于双重孔隙介质的假设,引入动态扩散理论,研究了瓦斯抽采过程中煤层瓦斯流场演化规律。综上所述,虽然多数学者针对某些因素对单个钻孔有效抽采半径的影响进行了深入的研究,但煤层渗透率各向异性对钻孔群抽采的影响却研究甚少。为此,拟采用数值模拟的方法,建立含瓦斯煤岩体的耦合模型,基于煤层的渗透率各向异性,分析钻孔群抽采过程中钻孔周围区域的瓦斯压力变化特征,分析渗透率各向异性对瓦斯运移的影响。
1 含瓦斯煤岩体的流-固耦合模型
瓦斯流动受多种因素影响,先做以下假设:①煤中只含有单组分气体;②瓦斯在煤层中流动为裂隙流动,符合达西定律[15];③视瓦斯为理想气体,其流动过程按照等温处理;④煤体骨架是线弹性体。
1.1 瓦斯渗流方程
瓦斯在煤层中流动符合质量守恒定律,其连续性方程可定义为:

式中:m 为煤体中游离瓦斯和吸附瓦斯含量,kg/m3;t 为时间,s;ρg为瓦斯密度,kg/m3;qg为瓦斯渗流速度,m/s;QS为瓦斯质量源汇项,kg/(m3·s)。
根据前人的研究[16-17],则有:
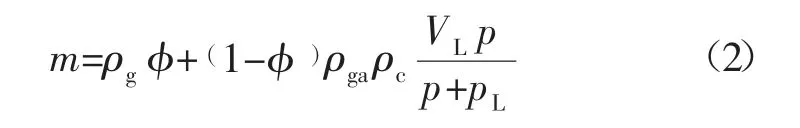
式中:ρga为标准状态下的瓦斯密度,;ρc为煤体密度,kg/m3;p 为瓦斯压力,MPa;VL为Langmuir 体积常数,m3/kg;pL为Langmuir 压力常数,MPa;φ 为煤层孔隙率,通常认为是动态变化的[18]。

式中:α 为等效孔隙压力系数;εv为体积应变;ks为煤体骨架模量,GPa。
在考虑Klikenberg 效应[19]基础之上,将式(2)~式(3)以及理想气体状态方程代入式(1)中可得瓦斯在煤层中的运移方程为:
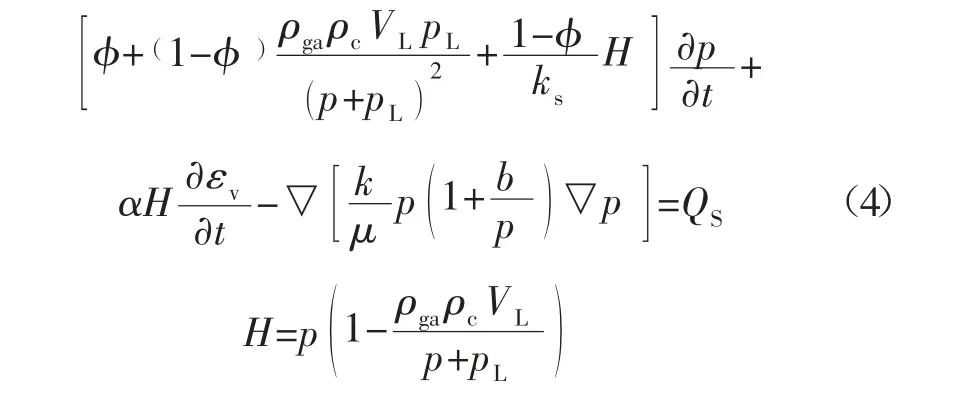
式中:k 为煤层渗透率,m2;μ 为瓦斯动力黏度系数,Pa·s;b 为Klikenberg 系数,Pa。
1.2 含瓦斯煤岩体控制方程
含瓦斯煤体是由分子颗粒及颗粒之间的间隙组成的孔隙介质,其变形符合弹性变形。
综合考虑了含瓦斯煤岩体弹性变形的本构方程[20]、煤体变形[21],以及有效应力规律[22],得到煤岩体变形控制方程:

式中:λ、G 为Lame 常数;ui、uj为i、j 方向的变形位移;v 为泊松比;σ 为总应力,MPa;fi为体积力,MPa;xi、xj为方向分量。
1.3 孔隙率和渗透率动态变化方程
在巷道掘进和钻孔施工后,煤岩体会发生变形移动,随着瓦斯抽采的时间不断增加,煤体内的瓦斯含量会不断降低,这些因素共同决定着煤层孔隙率和渗透率的变化。不考虑温度变化的影响,引入有效应力[23],同时考虑到瓦斯压力和吸附瓦斯解析引起的骨架变形[24],得到煤岩体的孔隙率变化为:
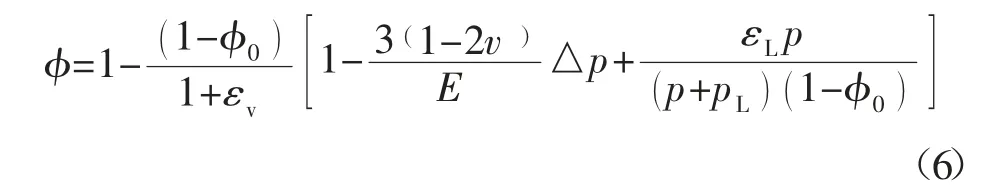
式中:φ0为初始孔隙率;△p=p-p0为瓦斯压力变化量,MPa;p0为初始瓦斯压力;E 为弹性模量,MPa;εL为Langmuir 体应变常数。
Kozeny-Carman 方程是建立渗流模型的基本依据,多孔介质的渗透率方程可以表示为:

将式(6)代入式(7),得到与孔隙率有关的渗透率方程:
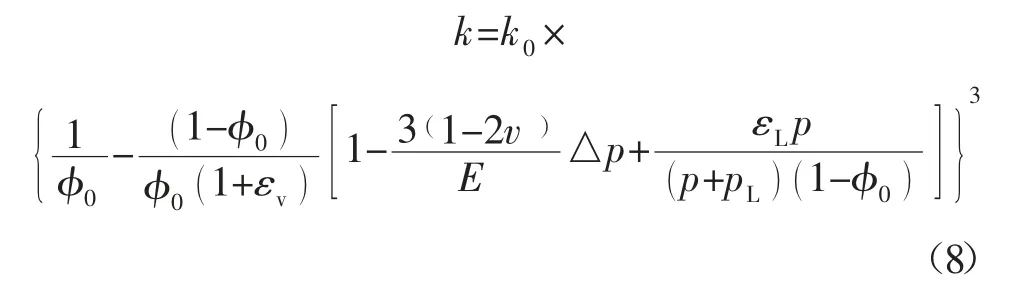
式(4)、式(5)、式(6)、式(8)即为瓦斯流动过程中的流-固耦合模型。
2 数值模型
2.1 几何模型
基于保德煤矿现场参数,利用COMSOL Multiphysics 软件建立几何模型,几何模型如图1。

图1 几何模型图Fig.1 Diagram of geometric model
模拟基本参数如下:①上部载荷:18 MPa;②动力黏度:1.08×10-6Pa·s;③弹性模量:2.59 GPa;④煤岩体密度:1 250 kg/m3;⑤瓦斯密度:0.716 kg/m3;⑥孔隙率:0.04;⑦泊松比:0.27;⑧瓦斯压力:1.21 MPa;⑨抽采负压:13 kPa。为表征煤层的渗透率各向异性,选取渗透率kx=1.645×10-15m2,ky=0.989×10-15m2。该模型长20 m,宽6 m,在模型中部施工3个钻孔,分别为1#、2#、3#钻孔,钻孔半径0.047 m。
2.2 初始条件与边界条件
1)初始条件:t=0 时,煤层瓦斯压力为1.21 MPa,初始位移ui=0(i=1,2),瓦斯在煤体内为层流流动。
2)边界条件:设四周边界无流动,模型的底部设置固定边界,两侧设为辊支撑,上部载荷σ=18 MPa。抽采负压为13 kPa。
3 模拟结果
为了更好地考察钻孔周围的瓦斯压力变化情况,在2#钻孔周围设置了监测线和监测点,监测线与监测点位置如图2。

图2 监测线与监测点位置Fig.2 Locations of monitoring lines and monitoring points
3.1 钻孔周围瓦斯压力变化特征
根据最新《防治煤与瓦斯突出规定》,选取瓦斯压力不大于0.74 MPa 的区域为有效抽采区域。
随着抽采时间的不断增加,煤层瓦斯压力也在随之降低,不同时间瓦斯压力变化高程图与等值线图如图3。

图3 不同时间瓦斯压力变化高程图与等值线图Fig.3 Elevation maps and contour maps of gas pressure change at different time
从图3 可以看出压力等值线图呈现出椭圆形状,表示不同位置的瓦斯压力不同,这种差异是由渗透率各向异性所导致的。渗透率大的地方瓦斯流动快,瓦斯压力的下降速率也快;渗透率小的地方瓦斯流动慢,瓦斯压力的下降速率相对缓慢。另外从高程图可以看出,钻孔形成后钻孔周围一定范围瓦斯压力迅速下降到0.74 MPa 以下,受后续抽采时间的影响小,这是由于在钻孔形成后钻孔周围形成了小范围的破碎区,瓦斯流动无阻碍。
监测线1 瓦斯压力随时间变化曲线如图4。从图4 可以看出,在30 d 时,2#钻孔周围仅有很小范围瓦斯压力小于0.74 MPa,其余位置的瓦斯压力均大于0.74 MPa;360 d 时,2#钻孔周围的瓦斯压力均都降到0.74 MPa 以下,以上现象表明距离钻孔中心越远,瓦斯压力越大,且随着抽采时间的增加,监测线上整体的瓦斯压力都随之降低。

图4 监测线1 瓦斯压力随时间变化曲线Fig.4 Changes of gas pressure with time on monitoring line 1
3.2 渗透率各向异性对瓦斯运移的影响
考虑渗透率各向异性和未考虑渗透率各向异性的不同时间瓦斯压力变化分别如图5 和图6。

图5 未考虑渗透率各向异性的不同时间瓦斯压力变化Fig.5 Variation of gas pressure at different time without consideration of permeability anisotropy
由图5 和图6 可知,在抽采30 d 时,由于抽采时间短,边界区域瓦斯压力未得到降低,存在最大瓦斯压力为1.21 MPa,即原始瓦斯压力;抽采90 d时,2 种情况下的瓦斯压力分布出现差异,未考虑渗透率各向异性时的抽采影响区域大,最大瓦斯压力为1.18 MPa,而考虑渗透率各向异性时的抽采影响区域相对小,最大瓦斯压力为1.19 MPa;在360 d时,未考虑渗透率各向异性情况下,2#钻孔周围的瓦斯压力全部降低至0.74 MPa 以下,抽采效果明显,整个模型左右边界区域最大瓦斯压力为0.87 MPa,而考虑渗透率各向异性时,在2#钻孔靠近模型上下边界区域内,瓦斯压力仍高于0.74 MPa,模型左右边界最大瓦斯压力为0.94 MPa。

图6 考虑渗透率各向异性的不同时间瓦斯压力变化Fig.6 Variation of gas pressure at different time with consideration of permeability anisotropy
为了研究渗透率各向异性对某一点抽采效果的影响,现分别对监测点1 和监测点2 的瓦斯压力变化情况进行分析,监测点1 和监测点2 上的瓦斯压力变化分别如图7 和图8。

图7 监测点1 上瓦斯压力变化Fig.7 Gas pressure change at monitoring point 1
从图7 中看出,在前100 d 的同一时刻,考虑渗透率各向异性情况的瓦斯压力pk略低,100 d 以后,未考虑渗透率各向异性情况的瓦斯压力pw小于pk,pw降低速率大于pk,在400 d 时,两者以相同的速率降低,有pk-pw=0.09 MPa,在抽采初期,2 个钻孔的共同抽采使得监测点1 的瓦斯压力迅速下降,在考虑渗透率各向异性时,其他方向上的瓦斯很难运移到监测点1,瓦斯的补充量低于未考虑渗透率各向异性时,故而在前100 d 有pw>pk;100 d 以后,渗透率各向异性对瓦斯运移所产生的作用越来越明显,渗透率越低,瓦斯在煤层中运移越慢。

图8 监测点2 上瓦斯压力变化Fig.8 Gas pressure change at monitoring point 2
从图8 可知,在同一时间有pk>pw,在300 d 以前,pk-pw不断增大,300 d 以后,pk-pw基本保持不变,有pk-pw=0.14 MPa。由于监测点2 在2#钻孔正上方,受渗透率各向异性影响最直接,且1#钻孔和3#钻孔对监测点2 的影响较小。比较图7 和图8 中的曲线可以发现,在考虑渗透率各向异性时,监测点1 的瓦斯压力达到0.74 MPa 需要270 d,监测点2的瓦斯压力达到0.74 MPa 需要350 d,因此在监测点1 瓦斯压力达标时,监测点2 瓦斯压力还未达标。
由于渗透率各向异性的存在,水平方向上渗透率大于垂直方向,由达西定律可知渗透率与达西速度qg成正比,即渗透率越大,达西速度随之增大。达西速度分布云图如图9,渗透率各向异性使得qg呈椭圆形分布,且越靠近钻孔中心,qg越大。在时间为30 d 时,qg最大值为0.82 m/s;90 d 时,qg最大值为0.7 m/s;180 d 时,qg最大值为0.61 m/s;360 d 时,qg最大值为0.48 m/s,由此可以看出,qg随着时间的增大而减小。达西定律直接表征了瓦斯在煤层中的流动,图9 中水平方向的达西速度大于垂直方向,表明p4>p3;qg随时间的增大而减小,这就使得整体瓦斯压力下降速率随时间增加而减小。
4 渗透率各向异性下的有效抽采区域
由以上分析可得到钻孔周围不同位置处的瓦斯压力分布规律。钻孔有效抽采区域分布图如图10。
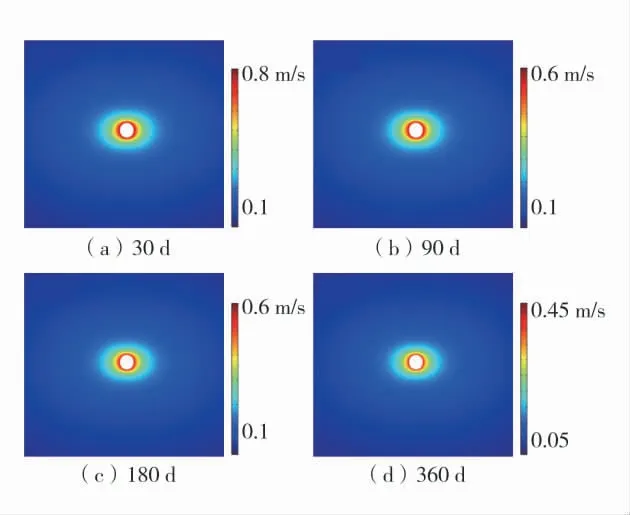
图9 达西速度分布云图Fig.9 Cloud map of Darcy velocity distribution
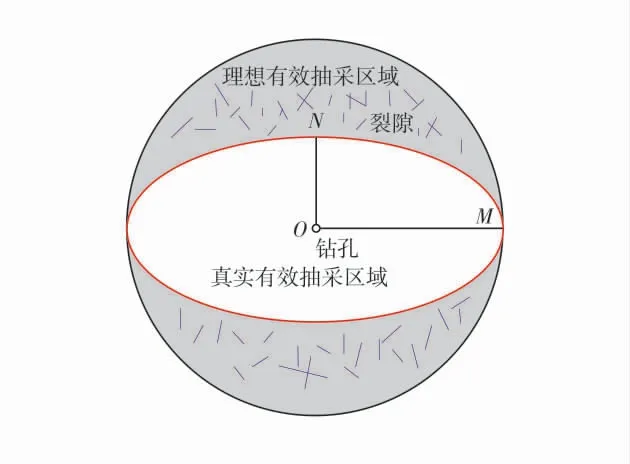
图10 有效抽采区域分布图Fig.10 Distribution of effective extraction areas
从图10 可知,椭圆形区域为根据模拟结果所得出的有效抽采区域,结合瓦斯压力分布云图5 和监测线2,监测线3 的瓦斯压力,可得最大抽采半径为椭圆长轴OM,最小抽采半径为短轴ON。以往的研究往往把以OM 为半径的圆形区域认为是钻孔的有效抽采区域。灰色区域为圆形区域与椭圆形区域之间的差集,由于煤体的渗透率各向异性,导致该区域并未处在有效抽采区域,即瓦斯抽采空白带。
在现场施工过程中应当充分考虑到上述问题,由于在垂直方向上渗透率较小,可以在钻孔施工过程中对垂直方向的煤体进行增透处理,增加煤体裂隙,增加其垂直方向上的有效抽采区域;还可以实施多层钻孔抽采,对下部钻孔进行卸压,可以有效降低灰色区域的瓦斯压力,降低瓦斯突出的风险。多层钻孔抽采如图11。
5 结 论
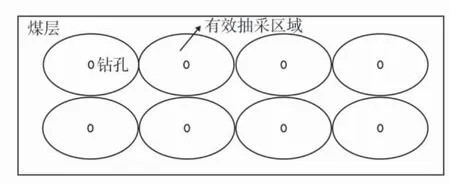
图11 多层钻孔抽采Fig.11 Multi-layer drilling
1)建立了瓦斯渗流方程、含瓦斯煤岩体控制方程、孔隙率和渗透率动态变化方程,在此基础上,得到含瓦斯煤岩体的流-固耦合模型。
2)钻孔周围不同位置处的瓦斯压力不同,瓦斯压力等值线图呈现出椭圆形状。钻孔周围小范围区域内处于完全卸压状态,瓦斯压力在短时间内下降到到0.74 MPa 以下。
3)在考虑渗透率各向异性时,监测点1 的瓦斯压力达到0.74 MPa 需要270 d,而在270 d 时,监测点2 的瓦斯压力为0.83 MPa,监测点2 的瓦斯压力达到0.74 MPa 需要350 d。
4)由达西定律可知渗透率与达西速度qg成正比,即渗透率越大,qg越大。30 d 时,qg最大值为0.82 m/s;90 d 时,qg最大值为0.7 m/s;180 d 时,qg最大值为0.61 m/s;360 d 时,qg最大值为0.48 m/s,故qg随着时间的增大而减小。
5)考虑渗透率各向异性的情况下,左右有效抽采区域大,上下有效抽采区域小,增透或采用多层钻孔抽采,可以增加有效抽采区域的范围。

