深部采空区煤层底板滞后破坏特征
张风达
(1.天地科技股份有限公司 开采设计事业部,北京100013;2.煤炭科学研究总院 开采研究分院,北京100013;3.中煤科工开采研究院有限公司,北京100013)
我国华北地区随着浅部煤炭资源的日趋枯竭,深部煤炭资源开采逐渐成为趋势,深部煤炭资源安全开采多面临着奥陶系承压灰岩水害的威胁。强烈采动扰动应力挤压部分底板岩体向采空区滑移变形,尤其是采空区周边因顶板“楔形”结构的存在而产生持续稳定的挤压作用,在一定程度上增大了煤层底板变形破坏程度,弱化了煤层底板阻水性能。当底板破坏区域与底板承压水导升区域连通时,将产生导水通道;在高承压水压力渗流和冲刷作用下导水通道的宽度逐渐增大,最终形成突水通道,诱发矿井底板突水。国内外学者针对煤层底板变形破坏展开了大量研究,主要代表性成果包括基于滑移线场理论建立的煤层底板剪切滑移破坏力学模型[1-3]、基于半无限体理论建立的煤层底板剪切破坏力学模型[4-7]、基于断裂力学理论建立的采场附近剪切破坏力学模型[8],以上研究主要从煤层底板岩体剪切破坏的角度进行了分析。关于工作面滞后变形破坏机理研究相对较少,目前主要有李海龙等[9]根据现场实测指出煤层底板存在二次扰动破坏;张风达[10-11],李春元[12-13],李浩[14]等通过理论计算、数值模拟等手段分析了深部煤层底板卸荷破坏机制。与此同时,部分学者对煤层底板突水机理也进行了研究,主要建立了隔水关键层[15]、十字交叉梁[16]、薄板[17-18]等力学模型和“下三带”[19]“下四带”[20]等概化模型,以上研究成果主要集中在煤层底板采动剪切滑移阶段和采空区卸荷破坏阶段,涉及采空区压实阶段的研究内容较少。采空区压实阶段的底板应力逐渐恢复,随着顶板垮落岩体的不断压实,原处于塑性阶段的煤层底板岩体存在再次发生破坏的可能性。为此,从理论分析、实验室试验、现场实测3 个方面探讨采空区煤层底板变形破坏特征。
1 采空区底板岩体破坏特征理论
受超前支承压力影响,一定范围内煤层底板的岩体产生压缩、剪切或拉伸变形,甚至发生破坏,该部分岩体以采动应力产生的滑移剪切变形为主,尤其是煤壁附近的煤层底板在超前支承压力的挤压和采空区卸荷膨胀的共同作用下产生剪切应力,加剧了煤层底板的变形破坏程度。随着距煤层底板距离的不断增加,底板岩体受采动应力影响程度和变形破坏程度不断减弱。处于塑性状态的煤层底板随着工作面不断开采,煤层底板采动卸荷影响程度不断增加,采动卸荷过程和采动卸荷后重新加载的过程中,煤层底板岩体仍存在变形破坏的可能性,为此,针对采动剪切滑移、采动卸荷和采动卸荷后重新加载3 个阶段的变形破坏特征进行分析。
1.1 基础力学模型
底板岩体内随机分布有不同角度的原生裂隙,在采动应力作用下,原生裂隙逐渐向某一固定角度进行扩展。假定采动裂隙与最大主应力方向的夹角为α,α=αm[21],αm=0.5arctan(1/f),f 为裂纹面的内摩擦系数。假定岩体最大主应力为垂直应力σ1,煤层底板岩体受力状态分析如图1。

图1 煤层底板岩体受力状态分析Fig.1 Stressed state analysis of coal seam floor
在最大主应力σ1、最小主应力σ3共同作用下,裂纹面的法向应力σn和剪切应力τn分别为:

式中:σ1为最大主应力,MPa;σ3为最小主应力,MPa;σn为法向应力,MPa;τn为剪切应力,MPa;α 为采动裂隙与最大主应力方向的夹角,(°)。
裂纹面所承受的剪切应力τ∞为:

式中:τ∞为裂纹面所承受的剪切应力,MPa;f 为裂纹面摩擦系数。
当岩体处于塑性临界状态时,其内部的部分原生裂纹发生扩展,但未形成贯穿裂纹,即采动应力已对岩体产生一定程度的损伤破坏。同时考虑到岩体在地层沉积过程中由多种矿物组成,且矿物晶体强度不同,因此,在裂纹面剪切变形过程中,出现沿晶破坏或穿晶破坏,致使剪切滑移变形过程中所形成的裂纹面往往不是1 个光滑的平移面,将裂纹面的粗糙突起定义为锁固段,将锁固段之间的平滑区域定义为滑移段。为此,将局部产生滑移变形且未贯穿破坏的裂纹面假定为由数个锁固段和滑移段组成,滑移变形裂纹示意图如图2。

图2 滑移变形裂纹示意图Fig.2 Schematic diagram of slip deformation crack
由图2 可以知道,剪切滑移变形过程中,锁固段是决定裂纹面滑移变形破坏的关键。为了简化计算,将图2 的某1 个锁固段(红色圆圈标示的A)简化为悬臂梁,忽略裂纹面爬坡对剪切应力的影响,分析其在裂纹面滑移过程中的变形破坏特征。悬臂梁模型如图3。

图3 悬臂梁模型Fig.3 Flexural cantilever model
根据弹性力学的悬臂梁模型,剪切应力τ∞对悬臂梁产生弯矩的M 为τ∞hbL(h 为悬臂梁高度,m),梁的截面惯性矩J 为:

式中:J 为截面惯性矩,m4;L 为悬臂梁宽度,m;b 为悬臂梁厚度,m。
距梁固定端距离y 的截面应力σ 为:

式中:σ 为悬臂梁距梁中心不同位置的应力,MPa;M 为悬臂梁弯矩,MN·m;x 为距悬臂梁中性轴的距离,m。
悬臂梁的最大拉应力位于梁的最外侧,最大拉应力σL为:

式中:σL为悬臂梁承受的最大拉应力,MPa。
由式(6)可知,梁截面宽度越大,最外侧拉应力越小;剪切应力和悬臂梁高度的越大,拉应力越大。
1.2 采空区底板岩体破坏特征
1.2.1 采动剪切滑移阶段
为直观分析采动应力对裂纹面锁固段完整范围的影响,假定原岩应力状态下的岩体已处于塑性临界,当剪切应力增大时,锁固段的局部将发生塑性破坏,此时悬臂梁最大拉应力σL=σb,σb为抗拉强度,MPa。悬臂梁模型在加载过程中变形破坏示意图如图4。在剪切变形程度进一步增大时,悬臂梁抵抗剪切变形的部分区域将发生塑性破坏,此时,悬臂梁抵抗剪切变形侧(图4 右侧)部分区域将因达到抗拉强度而发生拉伸破坏后,而未发生拉伸破坏的宽度为L′,梁的中性层向左侧移动。在悬臂梁塑性变形破坏过程中,消耗部分能量,实现了应力和应变相平衡。

图4 悬臂梁模型在加载过程中变形破坏示意图Fig.4 Deformation and failure of cantilever beam model during loading
为分析超前支承压力影响,并从计算简化的角度出发,假定超前支承压力作用下煤层底板岩体所承受的最大主应力为原岩应力ρgH 的2 倍,最小主应力由ρgH/2 增大至ρgH,将最大主应力2ρgH 和最小主应力ρgH 分别代入式(1)、式(2),并联立式(3)可得煤层底板岩体裂纹面锁固段承受的剪切应力τ∞′为:
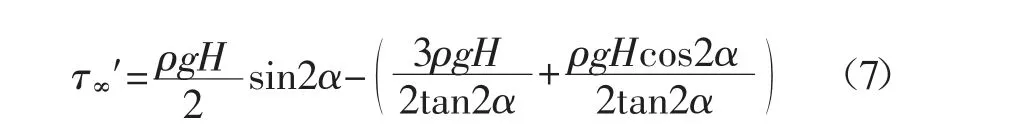
式中:τ∞′为超前支承压力作用下底板岩体裂纹面剪切应力,MPa;ρ 为上覆岩层平均密度,t/m3;H 为埋深,m;g 为重力加速度,m/s2。
相比于原岩应力状态下,锁固段所承受的剪切应力增量为:

式中:△τ∞为超前支承压力作用下锁固段所承受的剪切应力增量,MPa。
考虑到优势裂纹角α 小于45°,剪切应力增量恒大于0,说明受采动扰动应力影响下裂纹面承受的剪切应力增加,即已处于塑性临界状态的悬臂梁部分区域因达到抗拉强度而变形破坏,而悬臂梁未损伤区域L′断面处于塑性临界状态,根据理想弹塑性模型可知,塑性破坏区域的拉应力等于抗拉强度,联立式(4)~式(6)、式(7)得出未损伤区域L′:

式中:L′为超前支承压力作用下悬臂梁未损伤范围,m。
1.2.2 采动卸荷破坏阶段
随着工作面不断推进,处于超前支承压力影响范围内的底板岩体逐渐进入采空区,其应力状态由加载逐渐向卸载转变。煤层底板岩体在采场超前支承压力作用下产生一定程度的损伤破坏,随着卸荷程度的不断增加,部分岩体由三轴应力状态逐渐转变为双轴应力状态,垂直方向由原有的最大主应力逐渐转变为最小主应力,此时最大、最小主应力方向发生变化,剪切应力方向也随之发生变化。当剪切应力大于裂纹面滑动变形所需的滑动阻力时,将产生与原有滑动方向相反的滑动变形,裂纹面滑移变形与反方向滑移变形对比图如图5。

图5 裂纹面滑移变形与反方向滑移变形对比图Fig.5 Comparison of deformation crack surface between sliding and reverse sliding
由图5 可知,受采动卸荷影响,裂纹面向另1 个方向滑移,裂纹面间的锁固段原为拉伸变形的区域转变为压缩变形,为简化计算,忽略塑性变形区域对锁固段承载能力的弱化影响。
受采动剪切滑移变形影响,悬臂梁的有效承载宽度L′在卸载过程中,裂纹面发生反向滑移,当悬臂梁最左侧区域部分岩体拉应力达到抗拉强度并发生破坏时,悬臂梁有效承载厚度将进一步减小至L′′,悬臂梁模型在卸载过程中变形破坏示意图如图6。
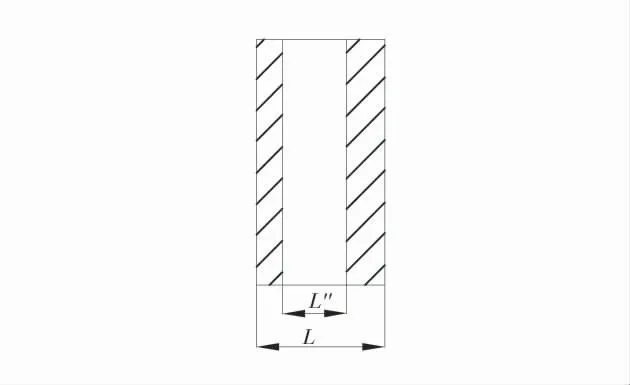
图6 悬臂梁模型在卸载过程中变形破坏示意图Fig.6 Deformation and failure of cantilever beam model during unloading
当裂纹面垂直应力卸载至0,而水平应力恢复至ρgH/2 时,水平应力变为最大主应力,最小主应力为0,将最大主应力、最小主应力分别代入式(1)、式(2),并联立式(3)可得此阶段锁固段所承受的剪切应力为:

式中:τ′∞为采动卸荷作用下底板岩体裂纹面剪切应力,MPa。
联立式(7)和式(10)可知,锁固段所承受的剪切应力增量为:

式中:△τ′∞为采动卸荷作用下锁固段所承受的剪切应力增量,MPa。
联立式(4)~式(6)、式(10),得出采动卸荷影响下完整的梁厚度L′′为:

式中:L″为采动卸荷作用下悬臂梁的未损伤范围,m。
1.2.3 采空区重新压实阶段
在采空区重新压实的过程中,煤层底板岩体受到二次采动影响,此阶段裂纹面滑动方向与采动剪切滑移阶段一致、与采动卸荷阶段相反。锁固段未损伤范围由L 减小至L″,此阶段的锁固段右侧损伤破坏区域经历了拉伸、压缩再拉伸的变形过程,锁固段左侧损伤破坏区域则经历了拉伸、压缩的变形过程。从能量耗散的角度出发,裂纹面剪切滑移或反向滑移变形过程中因锁固段部分区域拉应力达到抗拉强度而发生破坏,同时释放了部分能量,使得因外部载荷施加至锁固段所积聚的能量与之相平衡。在采空区重新压实的过程中,尽管从拉应力变化的角度分析,岩体不再发生变形破坏,但从能量积聚与耗散的角度分析,底板岩体仍存在变形破坏的可能性。为此,结合实验室试验和现场实测进一步分析采空区煤层底板变形破坏特征。
2 岩石变形特征力学试验
考虑底板岩体内部赋存有原生裂隙,承载能力原小于岩石。为分析深部采空区煤层底板加载至塑性状态后卸荷并重新加载过程中的变形破坏特征,结合峰峰某矿底板的砂岩开展岩石三轴力学试验,岩体平均埋深650 m,结合所处的应力状态,设定围压为8 MPa,将轴压加载至峰值强度的85%后(进入塑性阶段),卸载至20 MPa 并重新加载至破坏。卸载后重新加载偏应力-体积应变如图7。以压缩变形为正,膨胀变形为负。当体积变形量由压缩状态转为膨胀状态时,认为岩石进入塑性状态[22-23]。
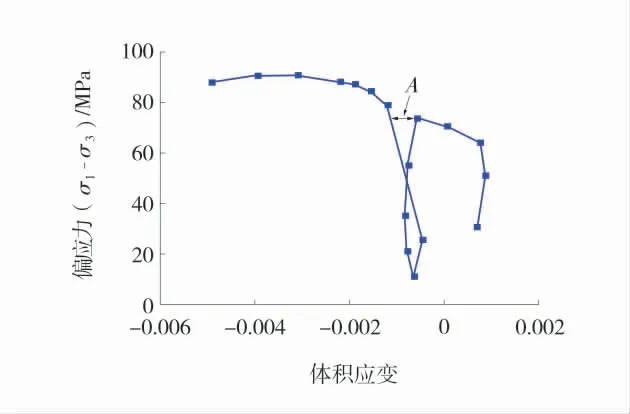
图7 卸载后重新加载偏应力-体积应变Fig.7 Deviator stress volume strain during unloading-reloading
由图7 可知,在岩样加载至塑性状态的过程中,随着轴向应力的不断增加,岩样的体积应变为先压缩后膨胀;在进入塑性状态后进行卸载,卸载时的偏应力为73.61 MPa(轴向应力81.61 MPa),岩样体积应变为-0.000 56,在偏应力由73.61 MPa 卸载至12 MPa 的过程中,体积应变整体略有减小;在重新加载至卸载时偏应力73 MPa(轴向应力81 MPa)左右时,体积应变约为-0.001 1,体积应变膨胀量约为-0.000 55,具体如图7 中的A。根据弹性力学可知,相比于卸载前的变形模量,卸载后再加载至相同应力的变形模量产生了明显劣化。即在重新加载至相同应力时,岩样的损伤程度明显增加。说明岩样加载至塑性阶段后卸载再加载的过程加剧了岩样损伤程度及其变形破坏的可能性。
3 深部底板破坏特征实测
煤层底板岩体内部在采动应力作用下产生大量的裂隙,导致其丧失部分或全部的阻水能力,即认为此状态的煤层底板岩体发生破坏。为此,通过峰峰矿区某矿112145 工作面开展的注水试验研究煤层底板变形破坏特征。该工作面平均埋深636 m,煤层平均厚度为4.2 m,煤岩层平均倾角为20°,工作面平均斜长为170 m。仅分析典型的、水平方向上距开切眼25 m 左右(初次来压影响范围)、垂直方向上距煤层底板18.19 m 的注水试验数据[24],将观测单位时间内钻孔漏失量换算为渗透系数,当渗透系数增量△K*≥0.2 m/d 时,认为底板岩体发生破坏[25]。随着工作面不断推进,距煤层底板18.19 m 处的岩体渗透性能不断变化,煤层底板注水钻孔渗透系数变化与其距工作面间距离的关系如图8。

图8 煤层底板注水钻孔渗透系数变化与其距工作面间距离的关系Fig.8 Variation of permeability coefficient of water injection hole of floor with different distances from panel
由图8 可知,当工作面推过钻场3.6 m 时,超前支承压力挤压煤层底板部分岩体向采空区方向滑移,煤层底板岩体产生部分采动裂隙,在一定程度上弱化了底板岩体的阻渗性能;随着工作面继续推进,采空区底板岩体受超前支承压力影响逐渐减弱,但底板所处的应力环境由高应力迅速转变为低应力,在超前支承压力作用下产生的采动裂隙在应力卸载过程中发生反向滑移变形,而且底板岩体在垂直应力逐渐卸载的过程中裂隙扩张,底板岩体的渗透性能进一步增大。当工作面推过钻孔15.8 m 时,采空区的覆岩未充分垮落,煤层底板岩体的应变变化与其应力变化基本协调一致,因此,在工作面推过钻孔15.8~24.7 m 的范围内,煤层底板采动扩展的裂隙逐渐恢复,此阶段的渗透性能基本恢复且无明显变化。当工作面推过钻孔24.7~30.9 m 的范围内,基本顶垮落重新压实采空区,对煤层底板岩体再次产生一定程度的应力扰动,煤层底板的渗透系数也随之变化。此现象验证了理论分析和实验室试验给出的岩体在塑性阶段卸载再重新加载的过程中,仍存在进一步变形破坏的可能性。
4 结 论
1)采用理想弹塑性力学本构模型,运用悬臂梁力学模型分析得出加载至塑性状态及卸载过程中锁固段的损伤范围呈逐渐增大的趋势。
2)轴压卸载前和卸载后重新加载至81 MPa 左右,岩样体积应变由原来的0.000 56 增大至0.001 1,说明加载至塑性状态后卸载再加载作用加剧了岩样内部损伤程度。
3)工作面推过钻场3.6~15.8 m 的范围内,煤层底板岩体在剪切变形和采动卸荷作用下发生裂隙扩张、变形破坏;工作面推过钻场24.7~30.9 m 的范围内,煤层底板岩体在采空区重新承载作用下再次破坏,验证了理论分析和实验室试验。

