考虑膜片弹簧非线性的干式离合器位置闭环控制*

张明远，陈 俐

（上海交通大学动力装置与自动化研究所，海洋工程国家重点实验室，上海 200240）

前言

干式离合器效率高、结构简单，作为传动控制部件广泛应用于机械式自动变速器、双离合器自动变速器和混合动力多能源耦合器等［1－2］。干式离合器的压力执行器大多通过膜片弹簧作用于压盘与摩擦片。为确保离合器部件发生一定程度磨损后仍具有足够的转矩传递能力，将膜片弹簧刚度设计成非线性，且在部分行程中为负值［3－4］。研究表明，负刚度会引起系统动力学失稳［5－7］，因而会降低离合器位置控制精度、引起摩擦片压力波动［8］，是降低离合器接合品质的一个重要因素。

针对离合器接合过程的控制，近年来，多种先进控制方法得到研究，比如，H∞鲁棒控制［9］、滑模控制［10］、模糊控制［11］、优化控制［12－13］和模型参考控制［14］等，这些研究未建立膜片弹簧特性模型，并假设离合器传递力矩或正压力可理想实现。文献［15］和文献［16］中基于离线实验获得膜片弹簧的非线性刚度，采用求逆函数的方法计算膜片弹簧的变形量，该方法利用了膜片弹簧的静态特性，但无法反映强非线性特性对动态响应的影响。文献［17］中将非线性特性嵌入位置控制回路，基于三步法设计了非线性控制策略；文献［18］中基于Udwadia-Kalaba理论，将离合器的接合规律视为约束设计了约束力的求解方法。这两种非线性控制算法较复杂，且缺乏对膜片弹簧负刚度的处理。

考虑膜片弹簧的非线性刚度直接影响离合器位置控制闭环的系统刚度与阻尼比，而膜片弹簧刚度特性可通过离线测量或在线辨识得到［19］，本文中提出了根据膜片弹簧局部刚度调整闭环反馈增益的思路，动态配置控制系统的极点，既防止因刚度为负导致失稳，又能使刚度非线性变化时控制系统能保持极点不动，算法较简单，却能使位置跟踪获得较好的动态性能。此外，考虑离合器位置控制系统满足微分平坦条件，为缩短响应时间，提高跟踪精度，本文中基于微分平坦理论设计了非线性前馈环节［20］。在MATLAB／Simulink平台上进行仿真，分别给出线性刚度、非线性正刚度和非线性负刚度3种特性下的开环响应和闭环控制结果，并将本文提出的非线性控制方法与两种未考虑膜片弹簧非线性刚度的传统控制方法相比较。以某大客车用干式离合器为试件进行实验，结果显示，由于负刚度的影响，膜片弹簧开环响应失稳。实施闭环控制，本文提出的非线性控制方法可克服失稳，且比传统控制方法精度高。

1 系统建模

本文中研究的干式离合器及其机电执行机构如图1所示，膜片弹簧中部被固定在离合器盖上，执行电机通过滚珠丝杠推动杠杆，杠杆推动推力轴承产生轴向位移，从而推动膜片弹簧的小端产生形变，大端相应产生压力，作用于压盘，控制压盘与摩擦片的分离与接合。

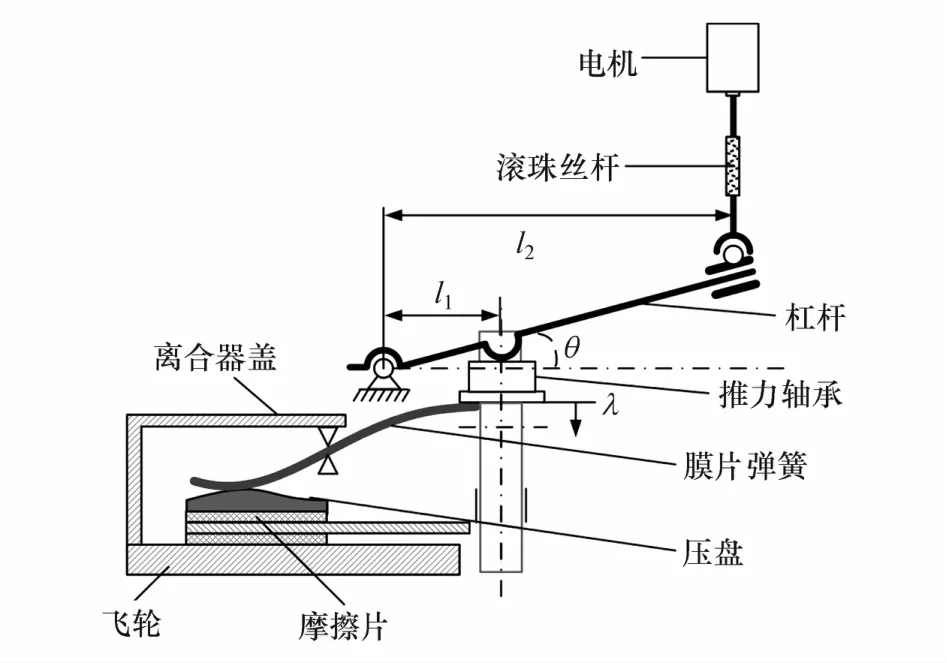
图1 干式离合器位置控制执行机构

1.1 动力学模型

电机驱动滚珠丝杠，带动杠杆绕支点转动的系统动力学方程［21］为

式中等效转动惯量J、等效阻尼系数c和等效力矩臂r的表达式如下：

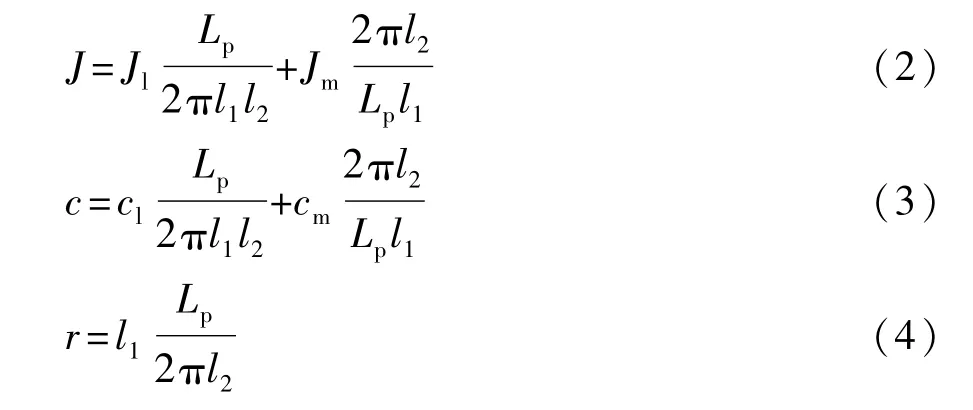
式中：Jl、Jm分别为杠杆、电机的转动惯量；cl、cm分别为杠杆、电机的阻尼系数；l1为推力轴承到支点的水平距离；l2为滚珠丝杠到支点的水平距离；Lp为滚珠丝杠的导程；Am为电机的转矩系数；Im为电机电流；λ为膜片弹簧小端的轴向位移，亦即小端变形量；F（λ）为膜片弹簧小端压力，随着小端变形量λ非线性变化。

膜片弹簧小端压力F（λ）与膜片弹簧变形量λ的非线性关系可通过实验测量得到，一款大客车用离合器的膜片弹簧小端压力的实测值见图2（a），可用三次多项式拟合：

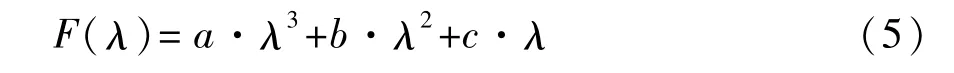
将压力F（λ）对膜片弹簧变形量λ求导，可得到膜片弹簧局部刚度的表达式为

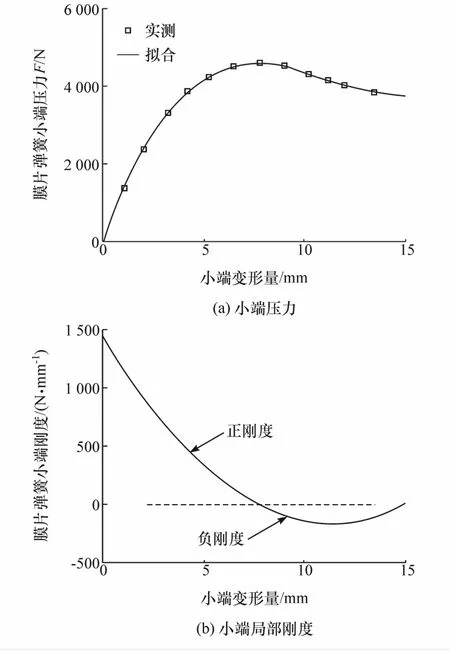
图2 膜片弹簧特性（a＝4.228，b＝－143.1，c＝1 445）

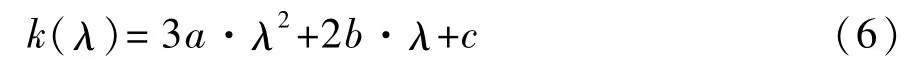
可见，膜片弹簧局部刚度k（λ）是膜片弹簧变形量λ的非线性函数，如图2（b）所示。当小端变形量约大于7.6 mm时，膜片弹簧局部刚度为负。

1.2 状态方程描述

令状态变量 x1＝λ，x2＝，控制输入量 u＝Im，根据式（1）方程写出被控对象的状态方程：

1.3 被控对象的稳定性

根据式（8）推导雅克比矩阵A的特征多项式：

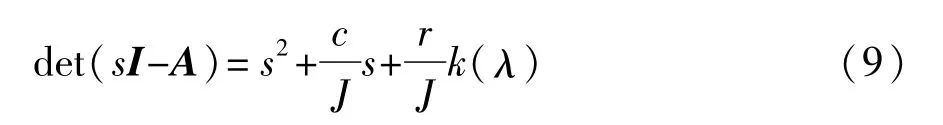
根据李雅普诺夫稳定性判据，如果矩阵A的所有特征值均具有负实部，则原非线性系统渐进稳定；如果A的特征值至少有一个正实部，则原非线性系统不稳定［22］。式（9）二次方程式有两个特征根，记为s1、s2，根据伟达定理，两根具有负实部需满足如下条件：

可见，当膜片弹簧局部刚度 k（λ）为正时，式（11）条件满足，离合器执行机构系统稳定；当k（λ）为负时，式（11）条件不满足，系统不稳定。

当系统不稳定时，需要设计合适的反馈增益使控制系统稳定，当系统稳定时，需要设计合适的前馈与反馈增益使控制系统实现快速、高精度的位置跟踪。

2 非线性控制器设计

本文中提出的离合器位置闭环控制框图如图3所示，包括前馈环节和反馈环节。基于微分平坦理论，本文中根据期望位置和膜片弹簧力与变形量之间的非线性关系设计前馈环节。基于极点配置方法，根据膜片弹簧非线性局部刚度k（λ）与位置反馈λ设计反馈增益的自调整机制。

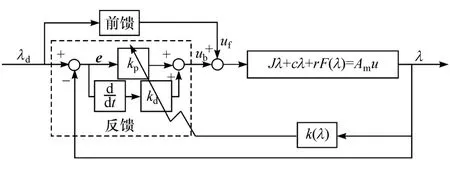
图3 离合器位置闭环控制框图

2.1 基于微分平坦理论的前馈设计

微分平坦理论提供了一种根据期望输出来设计前馈控制输入的方法。微分平坦理论在20世纪90年代针对非线性系统提出，并给出非线性系统动力学特性平坦输出的存在性［23］。

首先判断膜片弹簧离合器位置控制系统是否为微分平坦系统。选择系统输出量为膜片弹簧的小端变形量λ，即

根据式（7），系统的所有状态变量可用输出量y及其导数表示，即

因此，膜片弹簧离合器位置控制系统的所有状态变量和控制输入量均可由输出量及其有限阶微分表示。根据微分平坦理论，对于任意非线性系统，如果系统的状态变量和输入变量可由一组输出及其有限阶导数决定，则该系统为微分平坦系统［20］。

于是，按照微分平坦理论，可根据期望的输出轨迹λd，设计前馈输入为

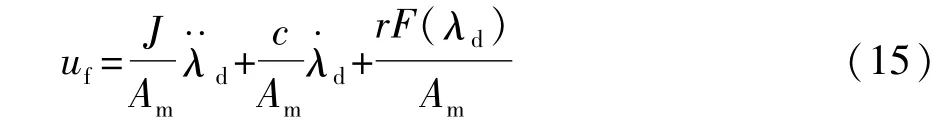
2.2 增益自调整的反馈设计

本节首先推导离合器位置闭环控制系统的稳定条件，然后应用极点配置方法，在稳定域中设计反馈增益的调整机制，使控制系统具有良好的动态性能。

2.2.1 闭环稳定性条件

定义位置闭环控制系统的误差向量e＝［e1e2］，且

考虑离合器位置控制的跟踪精度与快速性需求，选择比例、微分反馈控制，控制算法表达为

式中K＝（kpkd），kp和kd分别为比例反馈增益和微分反馈增益。

闭环系统的误差方程推导如下：

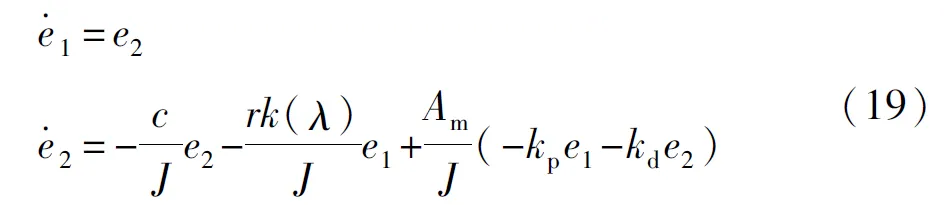
其矩阵形式为

根据李雅普诺夫稳定性判据，可得反馈增益kp、kd须满足如下条件：

按照上述条件选择反馈增益kd和kp，可使控制系统所有极点的实部位于负半平面，从而收敛。

2.2.2 增益自调整机制

调整闭环系统的阻尼比和固有频率，配置系统极点的位置，以期获得良好的动态性能。由式（22）特征方程可知，该系统是一个2阶系统，写成2阶系统的标准型式：

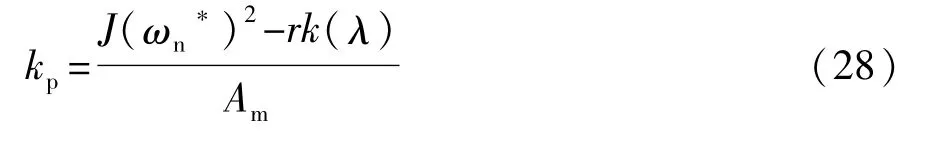
3 仿真结果与分析

本节给出 MATLAB／Simulink仿真结果。首先在开环控制下，使用3种不同刚度特性的膜片弹簧进行开环位置控制。其次，采用本文提出的控制方法对“快慢快”参考曲线进行离合器位置跟踪，控制结果与两种不考虑膜片弹簧非线性的传统控制方法相比较。

仿真用到的参数及取值见表1。

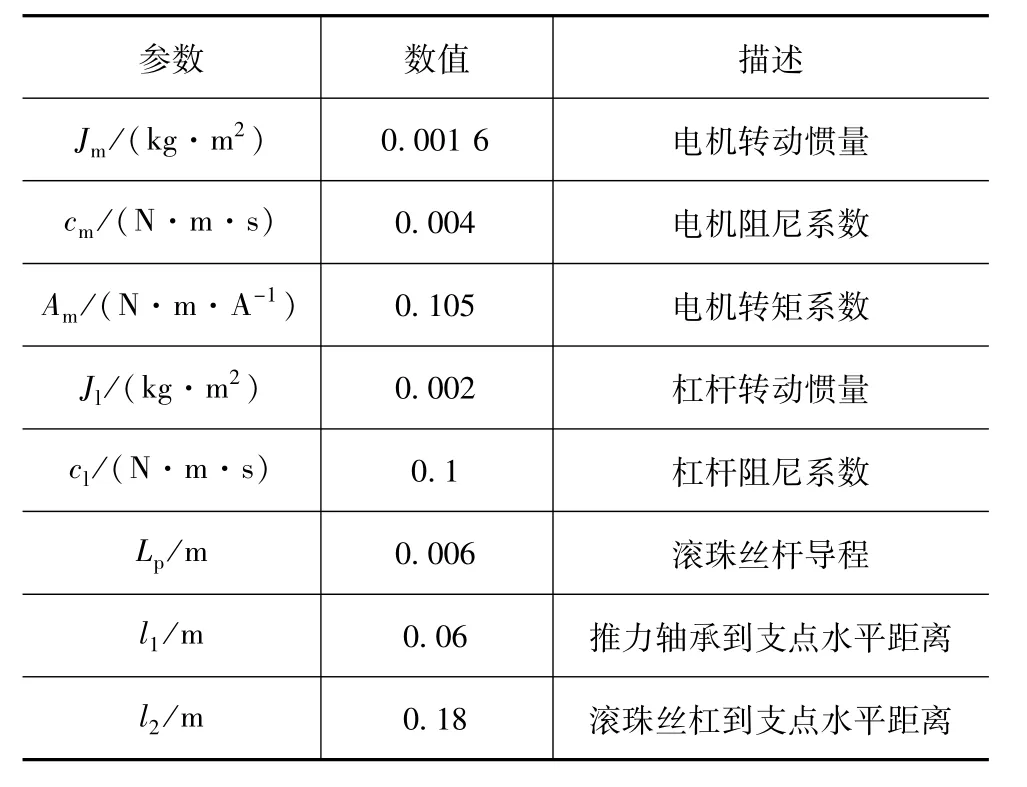
表1 执行机构仿真参数

3.1 开环控制位置响应

本节使用3个不同刚度特性的膜片弹簧进行仿真，其特性如图4所示，弹簧1具有非线性刚度，且具有局部负刚度区，弹簧2具有非线性，但全程刚度为正，弹簧3为线性，刚度为常数。

图4（b）给出在开环控制下，不同刚度特性的弹簧跟踪至6 mm位置的响应结果，开环位置控制对应的输入由微分平坦理论计算得到。开环结果表明，弹簧1没有稳定在目标位置，弹簧2、3虽然存在较大的超调振荡过程，但最终稳定在6 mm目标位置。弹簧1由于存在不稳定的负刚度区域，在超调振荡过程中进入了负刚度区域，使系统失去了稳定性，最终偏离参考位置。弹簧2、3的刚度始终为正，系统稳定，因此能收敛到目标位置。

3.2 位置闭环控制跟踪结果

以闭环系统稳定时间小于0.3 s、超调量小于5%为目标，确定系统参数 ζ*＝0.78＝12.82 rad／s［24］，然后按式（28）和式（29）计算自调整增益。本文提出的非线性控制算法的结果与两种传统的未考虑膜片弹簧非线性刚度的线性控制方法相比较。一种为前馈与比例微分反馈相结合的控制算法，增益按照初始位置的刚度设置；一种为广泛使用的PID反馈控制算法，增益未考虑膜片弹簧局部刚度变化。

为了比较，本文中给出了这3种方法对于3种不同刚度特性的膜片弹簧离合器位置跟踪的闭环控制结果，如图5～图7所示。当膜片弹簧刚度为非线性且含有负刚度区时，如图5所示，图5（a）中膜片弹簧小端变形量逐渐增大，但是从图5（b）可知，膜片弹簧小端压力在1.9 s后不增反降，反映了膜片弹簧负刚度的影响。从图5（c）可知，本文提出的非线性控制方法在整个行程中误差一直很小；而传统前馈结合反馈的控制方法，其微分与比例增益无法补偿负刚度引起的失稳，使误差在进入负刚度区域后急剧增大；固定增益PID方法，其比例增益可以补偿负刚度的影响，但由于缺少前馈，以及固定增益对动态参考输入的适应性欠缺，存在较大的稳态误差和较明显的滞后。

当膜片弹簧刚度为非线性但全部为正刚度时，结果如图6所示，非线性控制的跟踪误差最小，传统的前馈结合反馈的控制方法产生的误差仍然受到刚度变化的影响，固定增益PID反馈控制，存在较大的稳态误差和滞后。

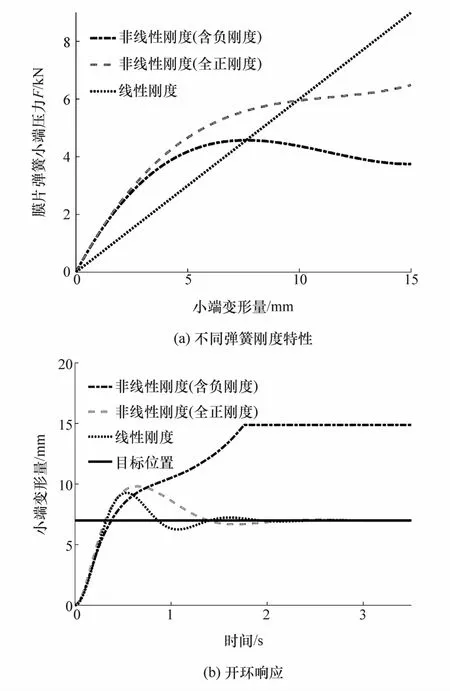
图4 弹簧刚度与位置跟踪开环响应的比较

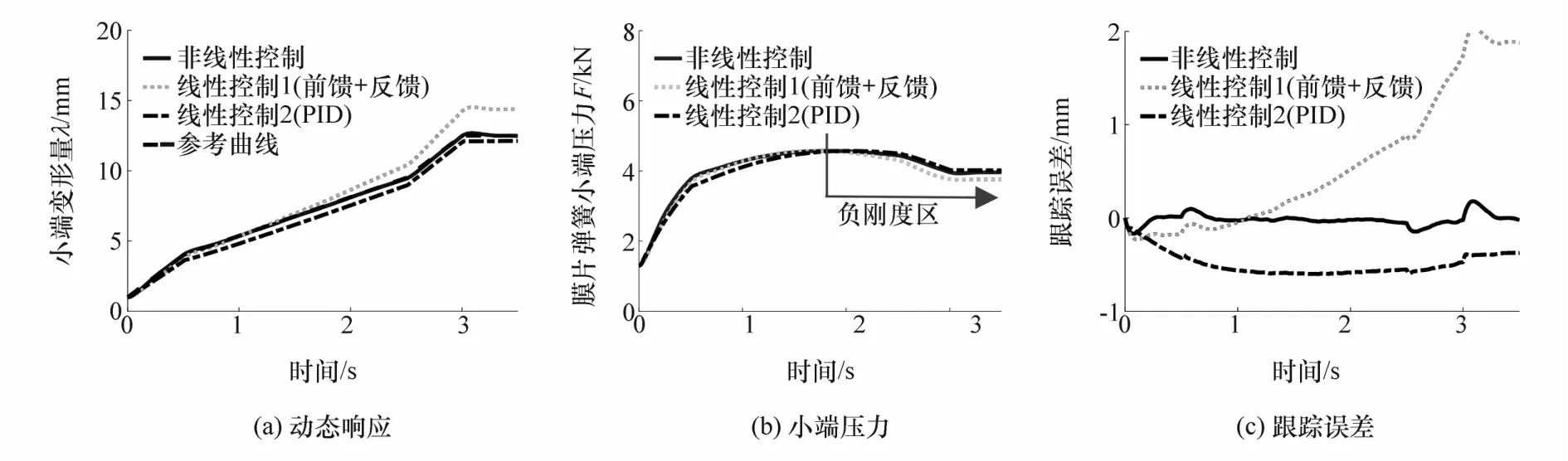
图5 非线性刚度（含负刚度）弹簧的离合器位置闭环跟踪

图6 非线性刚度（全正刚度）弹簧的离合器位置闭环跟踪

图7 线性刚度弹簧的离合器位置闭环跟踪

当膜片弹簧刚度为线性时，结果如图7所示。非线性控制与传统前馈结合反馈的控制方法得到的跟踪误差均较小，而固定增益PID反馈控制，仍然存在稳态误差以及时延较大的缺点。

由上述可知，由于考虑了非线性刚度的影响，本文提出的非线性控制方法在正刚度、负刚度和线性刚度情况下均能取得良好的跟踪精度；而由于不考虑非线性刚度的影响，传统的前馈结合比例微分反馈的方法仅在线性刚度情况下才取得较好的跟踪精度，固定增益PID方法的跟踪精度提高受到局限。

4 实验验证

本节以具有负刚度特性的膜片弹簧离合器为试件，实验装置如图8所示，控制算法在 MATLAB／Simulink中建立，通过快速原型控制器（dSPACE MicroAutoBox）自动生成代码下载至电机控制器，在上位机软件ControlDesk中可实时进行实验控制。采用压力传感器和位置传感器记录膜片弹簧小端压力和位置。

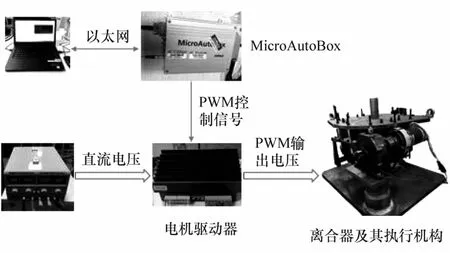
图8 离合器位置控制实验装置

开环控制结果如图9所示，膜片弹簧跟踪目标位置为6 mm，但膜片弹簧小端变形量偏离预期目标，反映了负刚度引起的局部失稳现象。

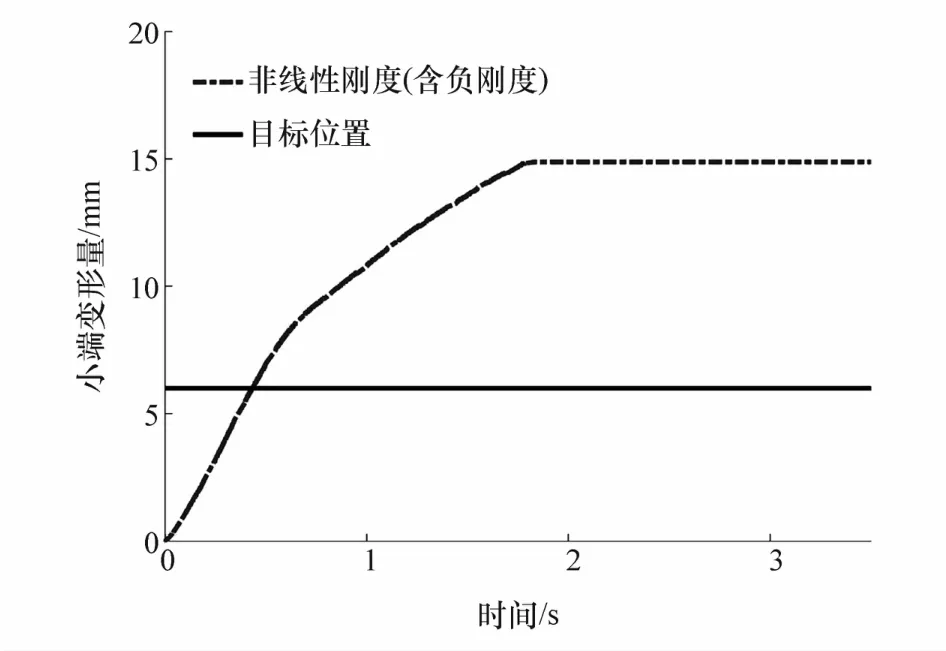
图9 开环响应实验结果

实施位置闭环控制，跟踪“快慢快”参考输入的实验结果如图10所示，反映的基本规律与仿真结果图5一致。本文中考虑膜片弹簧非线性刚度设计的控制策略跟踪误差最小，而不考虑膜片弹簧非线性刚度的前馈结合比例微分反馈控制表现出失稳，跟踪误差在进入负刚度区域后迅速增大，固定增益PID控制也受到负刚度影响有所增大。

跟踪正弦参考输入的实验结果，如图11所示，从图11（b）可观察到负刚度的明显影响，图11（c）表明，本文中设计的非线性控制策略跟踪误差也达到最小。

5 结论

本文中考虑离合器膜片弹簧刚度为非线性且在部分行程中局部刚度为负，首先建立了离合器位置控制执行机构的动力学模型，分析膜片弹簧负刚度对系统稳定性的影响，然后，考虑膜片弹簧的非线性，提出基于微分平坦理论设计前馈，并根据膜片弹簧局部刚度设计增益自调整反馈。仿真和实验结果均揭示了膜片弹簧进入负刚度区域的失稳现象。离合器位置闭环控制的仿真与实验结果表明，与传统的未考虑膜片弹簧非线性刚度的控制方法相比较，本文提出的控制方法可克服失稳，并具有较小的跟踪误差。

图10 跟踪“快慢快”参考输入的实验结果

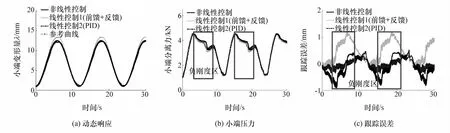
图11 跟踪正弦参考输入的实验结果