基于BP神经网络的不凝性气体对脉动热管传热影响的分析

陈静妍，徐荣吉，吴青平，王瑞祥，许淑惠

（1 北京建筑大学，建筑用能国家级虚拟仿真实验教学示范中心，北京100044；2 西安交通大学环境与能源工程学院，陕西西安710049）

作为高效换热元件，脉动热管（pulsating heat pipe，PHP）在电子器件散热[1-2]、太阳能热利用[3]、空调制冷[4]、余热回收[5]以及航空航天[6-7]等领域具有很大的应用潜力。而脉动热管的传热性能受诸多因素的影响，为提高其传热性能，从提出至今，国内外学者进行了深入研究[8]，主要包括工质热物性[9-12]、充液率[13]、不凝性气体[14-15]等因素对脉动热管的影响。Mohammad 等[10]认为应用表面活性剂可改善工质的性能，充液率为40%～60%时，脉动热管会有较好的传热性能。Ayel等[16]等实验论证了平板型脉动热管在垂直条件下具有更好的性能。在针对不凝性气体对脉动热管的研究实验中，曲伟等[14]通过可视化实验，研究了工质为二次蒸馏水的脉动热管运行特性，实验结果表明，不凝性气体的含量会显著影响脉动热管蒸发段和冷凝段的运行温度，从而对脉动热管的热阻产生影响。Raffles等[17]将乙醇作为工质，搭建了管径为1.5mm的一维双管段脉动热管物理模型，假定脉动热管为光滑直管段，壁面温度恒定，将热导率λeff作为脉动热管传热性能指标，将不凝气体含量较高时与不凝气体含量较低时λeff的减少量Δλeff作为不凝气体对传热影响的评价指标。通过数值模拟的方法对不凝性气体存在导致的脉动热管内部气泡的形成、气液塞的振幅以及Δλeff的影响做了研究。结果表明，随着不凝气体的增加，Δλeff呈线性减小的趋势，脉动热管内部气液塞的振幅和频率会减小，导致脉动驱动力减小，从而对其传热性能产生不良的影响，并实验论证了不凝性气体的存在会弱化脉动热管的传热性能[18]。尹大燕等[19]以无水乙醇为工质，通过改变不凝气体分压，对脉动热管热阻变化进行了研究。结果表明，不凝气体的增加会使脉动热管热阻的增大。郝婷婷[20]研究了超亲水表面及不凝性气体对脉动热管液弹脉动的振幅、速度和气液界面长度的影响，结果表明，随着不凝性气体含量的增加，脉动热管启动功率升高，液塞脉动振幅和速度降低，且冷凝段传热系数下降的振幅大于蒸发段传热系数下降的振幅，整体传热性能下降。在模型选择方面，Tafarroj 等[21]基于神经网络的方法对微通道的传热系数进行了研究。崔晓钰等[22]用神经网络方法搭建了脉动热管传热模型，论证了神经网络模型的可靠性。Wang 等[23]将蒸发段长度、热流密度等参数作为输入，搭建神经网络模型，对热阻进行预测。结果表明，实验和神经网络模型结果有较高吻合度，模型预测效果较好。张义林等[24]在对热管真空管集热器热性能的研究中，搭建了能够实现对其出口温度较为精准预测的BP 神经网络预测校正模型。颜卫国等[25]搭建了热管中冷器的BP 神经网络模型，对热管的传热阻力性能做了研究，研究结果表明，网络预测最大误差为8%。以上研究表明，BP神经网络模型在脉动热管传热系统中有较好的应用研究前景。

综上所述，不凝性气体的存在一方面会占据脉动热管内部有效空间，弱化流体的换热过程；另一方面会降低工质脉动强度，从而降低脉动热管的传热性能。因此有必要对其如何影响脉动热管传热性能的机理做出进一步研究。而且，脉动热管在实际应用过程中，存在一个安全的运行温度范围。而不凝性气体的存在会对脉动热管管内压力产生影响，继而对热阻以及蒸发温度产生影响。基于此，本文研究了工质为去离子水和聚丙烯酰胺（PAM）溶液时，不凝性气体对脉动热管传热和运行特性的影响规律，分析了影响机理。并将PAM 溶液作为研究对象，搭建了BP 神经网络模型，针对管内压力对脉动热管热阻和蒸发温度的影响作出了回归预测分析，同时对模型的可靠性做出了验证。基于神经网络的回归预测模型的建立，能够实现不同压力条件下对蒸发温度的预测，据此评估脉动热管内不凝性气体的含量，从而判断脉动热管是否失效。对于给定的脉动热管，在已知不凝性气体对其传热性能的预测模型后，可根据简单的运行参数，判断脉动热管的性能及是否失效，降低脉动热管实际应用成本。

1 实验系统及数据处理

1.1 实验系统

设计并搭建了半可视化脉动热管传热性能实验系统，如图1 所示，主要由脉动热管、电加热系统、恒温水浴冷却循环系统、数据采集系统组成。实验系统示意图如图2所示。其中，脉动热管主体部分为铜板，在铜板上铣出2mm×2mm的槽道，在其上部由厚度15mm的石英玻璃压紧，形成密封管路。在下部和上部分别贴紧加热模块和冷却模块，作为脉动热管的蒸发段和冷凝段，中间为绝热段（如图2所示）。脉动热管拼装完成后用玻璃丝棉保温并罩外壳，然后安装在可调节角度的支架上。

图1 脉动热管实验装置图

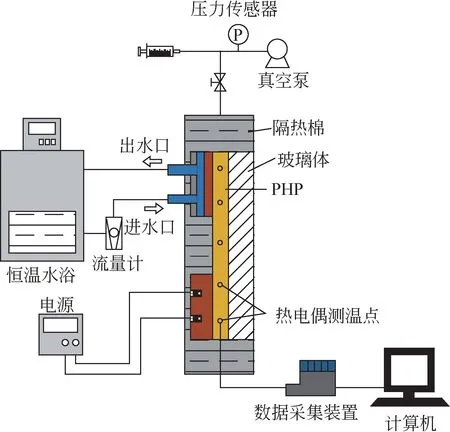
图2 脉动热管实验系统示意图

蒸发段采用电加热方式，供电电源为可编程直流电源M8853（75V/8A），通过调节输入电压来改变输入功率，脉动热管可实现的热流密度为40W/cm2。冷凝段采用恒温水浴提供的冷却水对脉动热管进行冷却，冷却水流量通过转子流量计（精度为2.5%）测得。压力传感器WIKAP-30（精度为0.05%）设在脉动热管冷凝段上部，可对抽真空后热管内部压力进行实时监测。采用安捷伦34972A 数据采集装置（精度为±0.1℃）和计算机实时对测温点温度进行采集。

图3 脉动热管实验系统示意图（T1～T10为测温点）

温度传感器采用精度为±0.1℃的T 形热电偶（OMEGA），共12只，在脉动热管铜板侧部设有深度为25mm的热电偶测温孔。其中脉动热管冷凝段设4只，编号为1～4；绝热段设2只，编号为5～6；蒸发段设4 只，编号为7～10；冷却水进水口和出水口各设一个测温点，如图3所示。

1.2 数据处理

脉动热管运行时的传热热阻R定义为式(1)。Te和Tc分别由脉动热管稳定运行时相应测点的平均值来确定，如式(2)和式(3)。

式中，Q 为加热功率，W；Te为蒸发段平均温度；Tc为冷凝段平均温度。

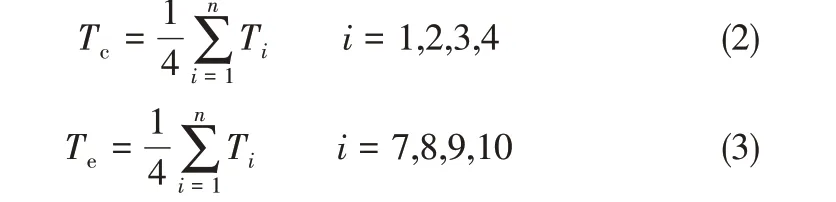
1.3 实验方法及工况

为了研究不凝性气体对脉动热管传热性能及运行特性的影响，保持充液率、倾斜角度、冷却水等实验条件不变，对脉动热管抽真空后充注工质，通过对脉动热管上部阀门的控制，使其内部混入一定量的不凝性气体来改变脉动热管内部压力，并用压力传感器对其进行实时监测和记录。脉动热管槽道内部为工质液体和工质蒸汽与不凝性气体的混合气体，由理想气体的分压定律，管内压力pPHP等于不凝性气体分压pa和饱和工质压力pW之和。充注完成后，脉动热管温度为20℃，水蒸气的饱和压力为2.338kPa。此时，不凝性气体的分压Pa如式(4)。

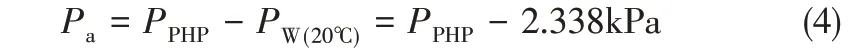
随着温度的变化，脉动热管管内压力、工质压力和不凝性气体的压力均会发生变化，且变化规律相似，为了清楚表述问题，认为充注完后不凝性气体分压力（20℃时）为不凝性气体分压力。充注完工质后脉动热管压力及实验设定工况如表1所示。

表1 实验设定工况

2 回归预测模型

2.1 BP神经网络模型

作为多层前馈神经网络，BP（back propagation）神经网络模型基于误差反向传播训练方式，包括输入端、隐层和输出端。其中，隐层是介于输入端和输出端的结构。通过输入n重样本数据，与隐层的连接权重产生结果，并作为输出层的连接权重和隐层间的输入，最后在输出端输出，这是正向传播过程。通过正向传播，可以在输出端节点处得到误差，误差作为输出端的输入进行反向传播，传播过程中模型能够对权重做出训练，得到最优结果，这个过程即为反向传播，如图4所示。

图4 BP神经网络传播原理简图

使用Matlab 软件进行模型的搭建，在此过程中，将管内压力和蒸发温度作为输入端变量，输入实验测得的管内压力数据和蒸发温度数据作为输入数据集（即样本），热阻作为输出参数，中间层（即隐层）为输入端和输出端的对应关系。实验测得的管内压力数据、蒸发温度数据和热阻数据作为用来训练的数据集，通过网格训练过程，对参数进行更新，从而使模型逼近真实的关系。输入与输出的关系可以表示为式(5)。

式中，P为管内压力；T为蒸发温度。

为了防止回归预测过程中的过拟合问题，对模型做出了噪声处理。最大训练次数设为5000，为了更加清楚地观察能量函数值的变化情况，结果中只呈现前1000次的训练情况。

2.2 训练过程

通过实验研究了PAM溶液分别在50～290W这7 个不同加热功率、5 个不同压力条件下的热阻和蒸发温度变化规律，得到5组实验数据（样本总数为35），并将此5 组数据作为研究神经网络模型的样本。在研究过程中，将其中的4 组作为训练集，1组作为验证集。在网络结构的设计上，将蒸发温度和管内压力值作为输入，热阻作为输出，因此输入层节点数为2（m），输出层节点数为1（n），根据式(6)，求得隐含层神经元数为5，其中a 为[1，10]之间的常数。网络结构如图5所示。

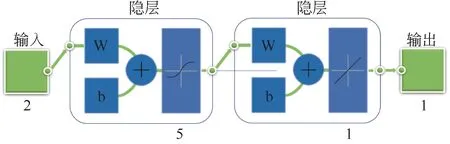
图5 网络结构

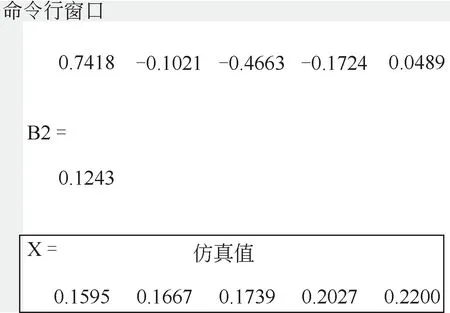
图6 命令行输出结果

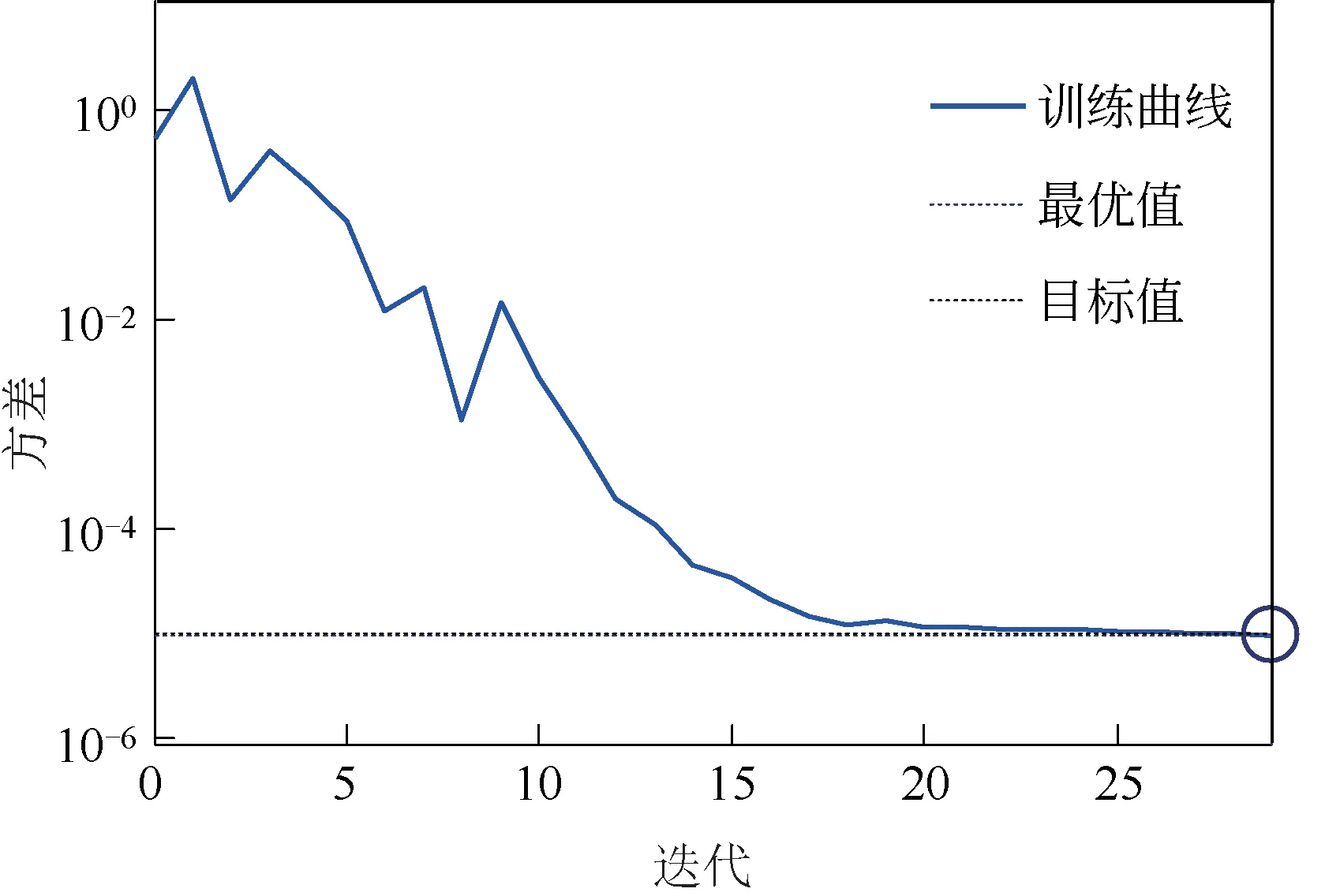
图7 29次训练后的误差期望曲线

以130W为例，输入训练集，通过tansig和purelin函数构建神经网络，网络训练函数为弹性梯度下降法trainrp函数。在网络参数的设定上，迭代次数设为5000 次，期望误差为1.0×10-5。图6 为训练后的命令行输出结果，其中X 为BP 神经网络仿真值，对比输出值可以看到二者非常接近。图7为网络经过29次重复训练，达到期望误差并完成训练。

2.3 反馈校正与评价

实际（实验）输出结果与神经网络训练结果会有误差存在。假设在n时刻，实际（实验）输出结果为y(n)，神经网络训练结果为ym(n)，二者之间的误差可表示为式(7)[26]。

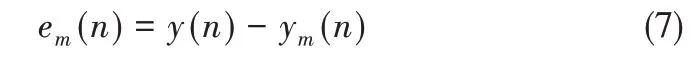
在误差较大的情况下，训练时间增加，训练结果收敛性较差，因此，在此情况下，需要根据实际（实验）输出结果对训练过程做出优化与修正。设α为优化系数，可根据实际情况做出调整，则修正后的结果可表示为式(8)[27]。

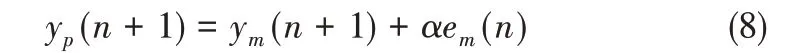
为了达到最优的预测训练结果，将能量（误差）函数作为评价预测结果的标准，将其函数最小值定为约束条件。图8 为加热功率为170W时，PAM 溶液的能量函数在训练神经网络过程中的变化图，能量函数图像结果显示了较好的预测结果。

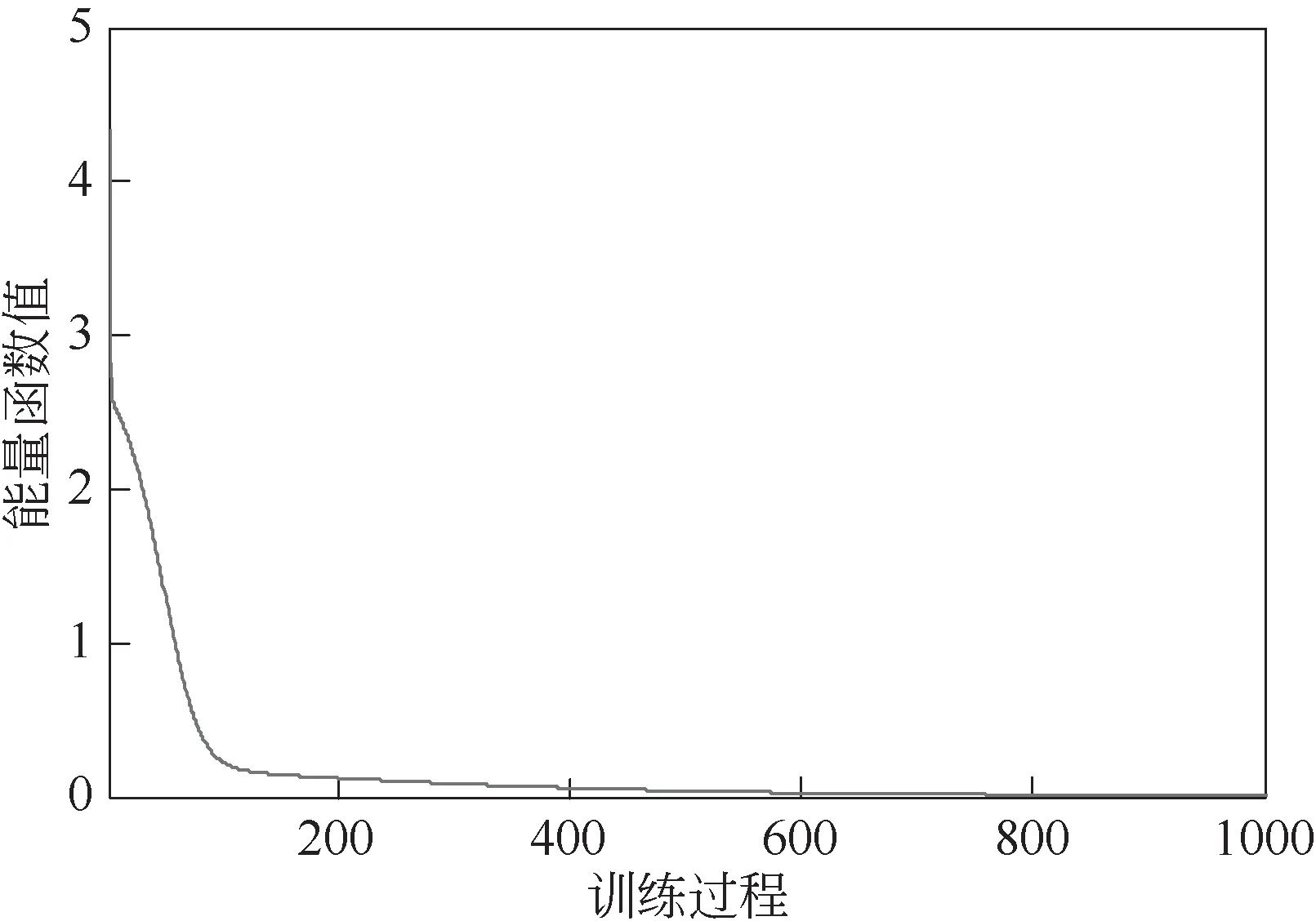
图8 能量函数在训练神经网络过程中的变化图

3 实验结果与讨论

3.1 不凝性气体对热阻的影响

图9是在不同加热功率条件下，分别以去离子水和PAM 溶液为工质的脉动热管热阻变化规律。由图可以看出，随着加热功率的增加，脉动热管的热阻逐渐减小。加热功率为290W时，充注了两种工质的脉动热管的最小热阻分别达到0.069℃/W 和0.075℃/W。在不同加热功率条件下，不凝性气体分压的增加使热阻增大。以去离子水为工质，在加热功率为250W 的条件下，不凝性气体分压由0.892kPa 变化为1.212kPa 时，热阻由0.079℃/W 变化为0.094℃/W。

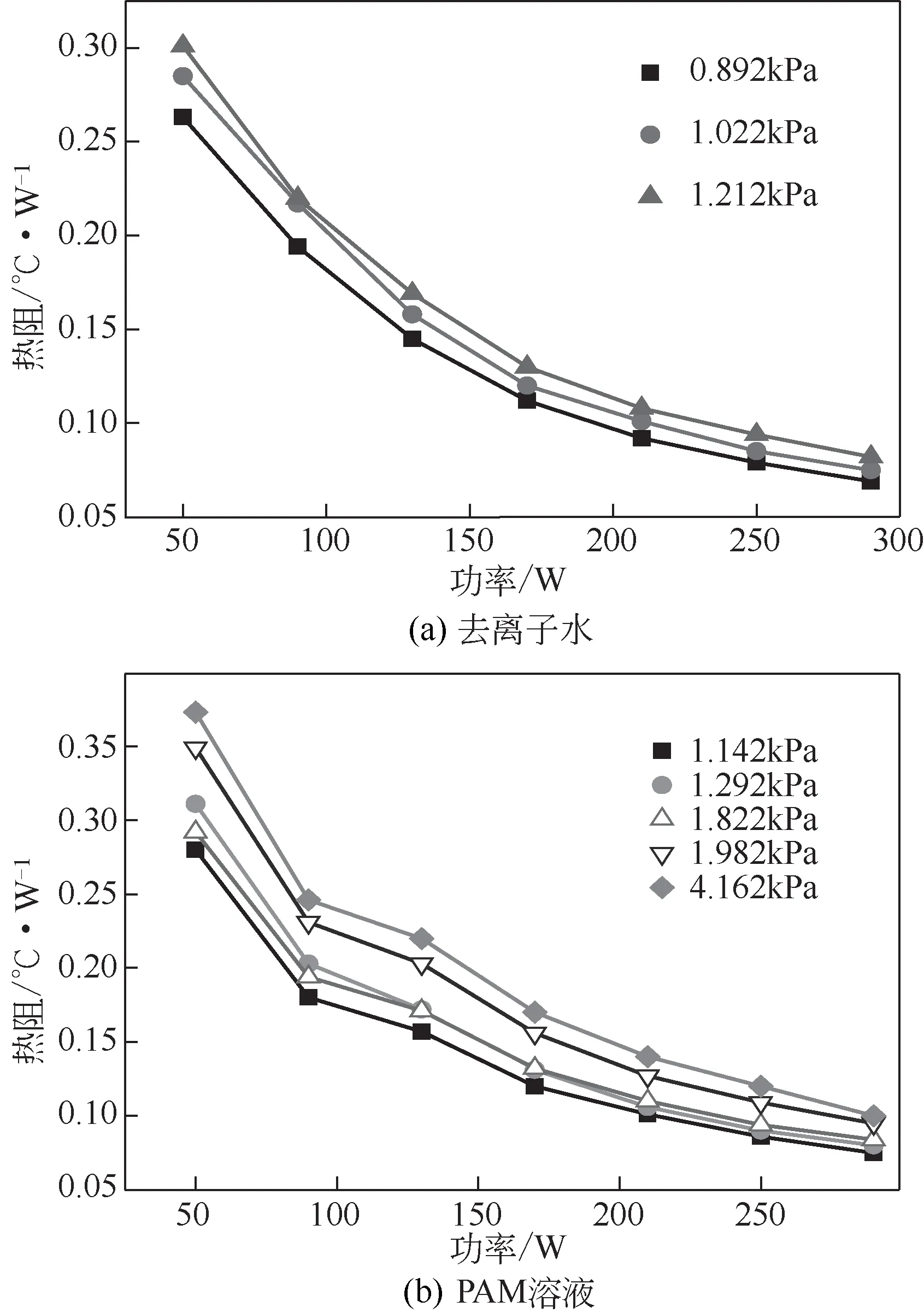
图9 不同加热功率条件下不凝性气体对脉动热管热阻的影响

图10 是分别以去离子水和PAM 溶液为工质，在不同不凝性气体分压力条件下，不凝性气体对脉动热管的热阻影响规律。从图中可以看出，不凝性气体的存在对热阻有较大影响。随着不凝性气体分压力的增加，脉动热管的热阻呈增加趋势，斜率随着加热功率的增加而减小，也就是说在加热功率较高的条件下，不凝性气体对脉动热管热阻的影响减小，与文献[11]研究结论相同。在加热功率为290W、以PAM溶液作为传热工质且不凝性气体分压力为1.142kPa 时，脉动热管热阻最小，为0.075℃/W。从传热学角度来分析，气体的热导率小于液体，不凝性气体的存在限制了流体的换热，导致有效换热量减小，换热效率降低，热阻增大。

图10 不同压力条件下不凝性气体对脉动热管热阻的影响

3.2 不凝性气体对脉动热管蒸发温度的影响

图11(a)为加热功率为210W、以去离子水为工质的脉动热管在稳定运行时，不同不凝性气体分压力条件下脉动热管蒸发温度变化曲线。从图中可以看出，不凝性气体的存在对脉动热管蒸发温度影响较大。当脉动热管的不凝性气体分压力为0.892kPa时，脉动热管蒸发段温度最小，平均温度为59.2℃；当不凝性气体分压为1.212kPa 时，脉动热管蒸发温度最大，平均温度62℃。

图11 不同压力条件下不凝性气体对脉动热管蒸发温度的影响

图11(b)是以PAM 溶液为工质的脉动热管在稳定运行时不同不凝性气体分压力条件下脉动热管蒸发温度。由图可以看出，当不凝性气体分压力为1.142kPa时，脉动热管蒸发段温度最小，平均温度为60.9℃；当不凝性气体分压力为4.162kPa时，脉动热管蒸发段温度最大，平均温度为69.4℃。

不凝性气体的存在对蒸发温度的影可以从两方面考虑。一方面，由于不凝性气体的存在使脉动热管管内压力高于工质的饱和蒸汽压，因此需要更高的蒸发温度来驱动运行过程。另一方面，不凝性气体占据了脉动热管内部空间，液体汽化做功（吸热量）增加，因此导致了蒸发温度的升高。

3.3 回归预测与验证

3.3.1 模型预测

将脉动热管管内压力、蒸发温度样本集作为神经网络的训练集，基于训练后的神经网络模型对热阻做出预测，得到网络输出热阻。图12 为加热功率为170W，工质为PAM溶液时的网络输出热阻与实际热阻对比以及预测（预测管内压力为7kPa 和8kPa）。通过式(7)计算预测误差，在170W 的条件下，通过神经网络模型预测得到的网络输出热阻与实际热阻之间的误差分别为0.05%、0、0.02%、0.07%、0.02%，网络输出热阻与实际热阻一致性较好，因此不需要通过式(8)对模型做出优化与修正。

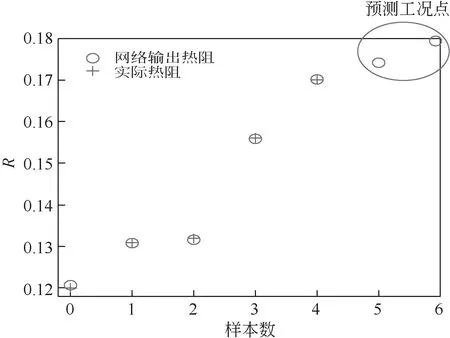
图12 网络输出热阻与实际热阻对比以及预测图像

从图中可以看出，在加热功率为170W时，设定不同的管内压力（7kPa 和8kPa）工况，可以对热阻做出预测，管内压力为7kPa 时，热阻预测结果为0.174℃/W；管内压力为8kPa时，热阻预测结果为0.178℃/W。

3.3.2 验证分析

为了验证回归模型的可靠性，对模型做出了反向预测，即通过热阻对脉动热管管内压力做出预测（验证）。表2 为加热170W 时，反向预测误差检验结果。表中P-R 表示通过设计压力对热阻预测结果，R-P表示通过预测热阻对管内压力预测（反向检验）结果。

表2 加热功率为170W时，反向预测误差检验

从表2可以看出，设定管内压力分别为7kPa和8kPa 时，通过两种预测模型下的预测值之间的差值分别为9.92%和3.87%，误差在可接受范围内，证明BP神经网络预测是可靠的。

3.3.3 不同加热功率、不同管内压力脉动热管热阻预测

基于实验数据对低加热功率（50W、90W、130W、170W）和高加热功率（210W、250W 和290W）7 种工况条件下，管内压力为7kPa 和8kPa时，应用PAM 溶液的脉动热管传热性能进行了预测，结果汇总于表3。由表3可以看出，BP神经网络在不同加热功率下，均能对不凝性气体对脉动热管传热性能影响作出较为准确的预测，特别是在训练值范围外，显示出BP神经网络的广泛适用性。

表3 不同加热功率下PAM溶液脉动热管传热性能预测

3.3.4 不同加热功率、不同管内压力脉动热管蒸发温度预测

基于实验数据，选用低加热功率（50W、90W、130W、170W）和高加热功率（210W、250W 和290W）7 种工况条件，在管内压力（预测压力）为7kPa和8kPa时，应用PAM溶液的脉动热管的蒸发温度进行预测。基于预测结果，并对管内压力和蒸发温度之间的关系作出了线性拟合。图13 分别为低加热功率和高加热功率条件下管内压力与蒸发温度的拟合图。

通过使用Matlab软件，分别对低加热功率和高加热功率时，脉动热管蒸发温度随管内压力变化做出了预测，结果表明，随着管内压力的增加，蒸发温度升高。进一步地，为了实现较为精确的预测，对二者之间的关系作出了线性拟合。从图13 可以看出，低加热功率时，蒸发温度的线性变化呈现出较为一致的增加趋势。当采用高加热功率时，管内压力与蒸发温度的线性关系呈现出加大的增加强度。结果表明，高加热功率脉动热管的蒸发温度更容易受到管内压力变化的影响，而低加热功率能够弱化管内压力变化对脉动热管传热的影响。在低加热功率时，线性拟合可分别表示为式(9)～式(12)。

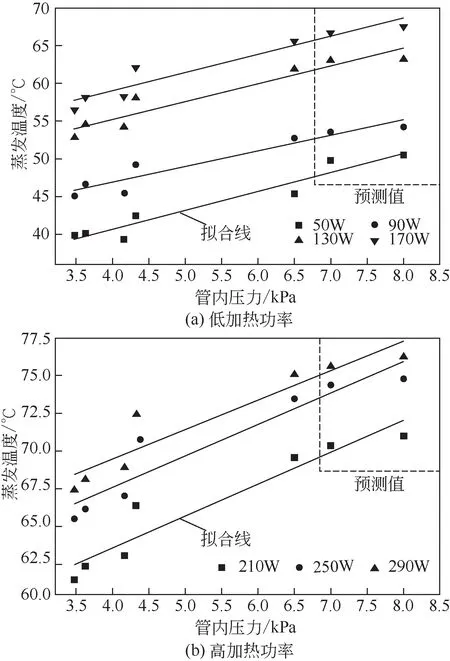
图13 管内压力与蒸发温度的预测与回归

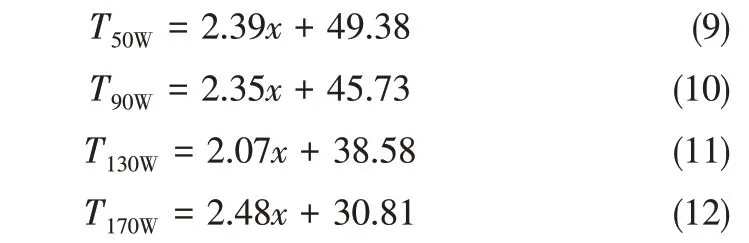
在高加热功率时，线性拟合结果可分别表示为式(13)～式(15)。

式中，T 为脉动热管蒸发温度；x 为脉动热管管内压力。

4 结论

（1）不凝性气体影响脉动热管传热性能。以去离子水作为传热工质时，随着加热功率的增加，脉动热管热阻减小。当加热功率增加到290W时，最小热阻达到0.069℃/W。不同加热功率下，随着不凝性气体分压力的增加，脉动热管热阻增大。

（2）以PAM 溶液为加热工质时，随着不凝性气体分压的增加，脉动热管热阻增大，且在较高加热功率下，不凝性气体对脉动热管影响减小。当不凝性气体分压为1.142kPa时脉动热管热阻最小，为0.075℃/W。

（3）不凝性气体对脉动热管蒸发温度影响较大。不凝性气体的存在使脉动热管管内压力高于工质的饱和蒸汽压，提高了其对应的蒸发温度。

（4）BP 神经网络模型的预测结果表明，脉动热管管内压力与热阻、管内压力与蒸发温度都存在正向的相关关系，且关系是可靠的。通过回归预测模型，可以较好地对热阻和蒸发温度（管内压力）作出预测，并且对脉动热管的运行状态作出预判。

符号说明

a—— [1，10]之间的随机数

em—— 误差

l—— 隐含层神经元数

m—— 输入层节点数

n—— 输出层节点数

p—— 压力，kPa pa，pW，pPHP—— 分别为不凝性气体分压力、工质压力和管内压力，kPa

Q—— 加热功率，W

R —— 传热热阻，℃/W

T —— 温度，℃

Te，Tc—— 分别为蒸发段平均温度、冷凝段平均温度，℃

Y(n)—— 实际（实验）输出结果

Ym(n)—— 神经网络训练结果

α—— 优化系数