基于重要度分析的数据预处理方法及风机有功功率预测研究

葛滨

基于重要度分析的数据预处理方法及风机有功功率预测研究

葛滨

（河北工业大学 人工智能与数据科学学院，天津 300401）

以风力发电机的有功功率预测为研究对象，在考虑了功率损耗及环境因素的情况下选取17组参数指标作为输入，以功率负荷等级为分类指标，采用随机森林分类算法进行参数属性的重要度分析，根据权重系数的阈值设定构建功率预测的样本数据库。基于集成学习Bagging算法的思想，分别选择支持向量机（Support Vector Machine，SVM）、极限学习机（Extreme Learning Machine，ELM）和随机森林回归算法为基学习器。提出了一种基于遗传算法的动态加权的集成学习策略，构建基于集成算法的有功功率预测模型。分别根据正常功率和限功率样本数据库，进行集成算法模型的实例验证和性能分析比较。

风电；随机森林；基学习器；集成学习算法

风能作为无污染的可再生能源，被广泛应用于发电领域。实现风电机组发电功率的准确预测，对提高风电机组的并网发电效率和促进电力系统平稳安全运行都具有非常重要的现实意义。

中国在许多重要的风电技术上还处于探索和积累阶段，但近些年在新增和累计装机容量上已保持了高水平发展。目前中国有中国电力科学院在2008年推出的首个自主研发预测系统WPFS Ver1.0、国网南瑞研发的WPFS系统和由华北电力大学开发的SWPPS系统。虽然国内外对风电功率预测的研究工作已较为成熟，但参考现有方法预测输入仍为以风速为主的少数因素，缺乏对多维输入因素的研究。

本文基于随机森林算法对参数属性进行重要度分析，选取SCADA中的重要输入参数，提出利用集成学习算法构建风电功率预测模型，该模型速度快、泛化能力强、收敛速度快、准确度高，并通过实验数据验证了该预测方法的可 靠性。

1 基于随机森林算法的特征重要性评估

常见的计算方法有两种，一种是平均不纯度的减少（mean decrease impurity），常用Gini、entropy、information gain测量，现在sklearn中用的就是这种方法；另一种是平均准确率的减少（mean decrease accuracy），常用袋外误差率去衡量。

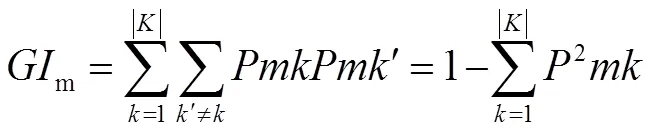
在式（1）中，表示有个类别；表示节点中类列所占的比例，即随便从节点中随机抽取两个样本，其类别标记不一致的概率。特征j在节点的重要性，即节点分支前后的Gini指数变化量。

式（2）中：l和r分别为分枝后两个新节点的Gini指数。

平均准确率的减少即对每个特征加噪，看对结果的准确率的影响。影响小说明此特征不重要，反之重要。具体步骤如下：①对于随机森林中的每一棵决策树，使用相应的OOB（袋外数据）数据来计算它的袋外数据误差，记为1。②随机地对袋外数据OOB所有样本的特征X加入噪声干扰（即随机的改变样本在特征X处的值），再次计算它的袋外数据误差，记为2。③假设随机森林中有棵树，那么对于特征X的重要性计算如公式（3）所示。若给某个特征随机加入噪声之后袋外的准确率大幅度降低，则说明这个特征对分类结果影响大，重要程度较高。

Σ（2－1）/（3）

2 基于集成学习算法的风电功率预测模型

集成学习模型的构建通常可以分为两个步骤：个体模型生成与模型融合。

本文选用SVM、ELM和RF作为个体学习模型。对于SVM模型，利用SVM+GA的形式，通过GA算法对SVM惩罚参数和径向基核函数的参数进行寻优求解，利用得到的最优参数完成SVM模型的训练。ELM和RF模型利用与SVM相同的数据完成回归模型的训练，并对三种模型的训练结果进行分析，总结各个模型的优缺点，为集成策略的选择提供前提。

本文利用基于PSO动态加权融合的方式。首先从验证集集合中选取与测试集相似的若干样本，将其作为个体模型的输入，根据输出结果，评估个体模型在这些数据上的预测误差。预测输出值公式为：

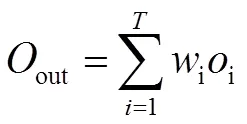
式（4）中：out为预测值集成后输出的向量；为参加训练的个体模型数；i为权值；i为每给个预测结果。

将这些数据的真实功率与预测功率作为PSO算法的一个输入，将真实功率与预测功率的均方差误差作为PSO目标函数。目标函数为：

式（5）中：为预测个数；out_i为第个数据的预测值输出；i为实际功率值。

基于PSO算法可以很方便地找到一组各个模型间的融合加权系数。假设得到的动态加权系数为，则可以利用对各个模型的预测结果经动态加权集成，得到最终结果。

3 实验结果及分析

本论文选用河北某风电集控中心在2019-03—2019-12 SCADA系统采集的824组历史数据，进行初步预处理后保留803组数据。利用随机森林算法对全部样本进行功率分类预测误差分析，得到最终分类预测分析结果准确率为89%。此时利用随机森林算法根据公式（3）对17种输入参数进行基于平均准确率减少的重要性评估。

根据影响预测结果的重要因素风机运行状态，将全部样本分为限功率和正常功率两组，重复上述数据处理流程，决策树迭代次数分别达到20次和40次时函数收敛，分类预测准确率为95%和98%。预测准确率较全部样本分析时得到显著提高。根据样本参数属性重要度数据及权重，样本取权重大于0.05的参数作为最终输入因素。构建正常功率预测决策表，如表1所示。

表1 正常功率预测决策表

属性类别实时风速风轮转速风向与轴夹角实际扭矩空气密度线圈电流 权系数0.270.2660.1330.120.080.05

将414个正常功率样本数据随机分成两部份，选取300个作为训练样本数据并完成SVM、EML和RF基础学习器的训练，剩余114个作为检测样本数据完成对算法模型的验证。首先对SVM模型进行训练，本文利用GA算法对SVM分类器进行最优求解。在实验中，设置GA算法的最大迭代次数为150，种群最大数量为40。利用寻找到的最优参数对SVM进行训练，设置为3.002 8，gamma为0.138 38。通过对比误差量，表明训练模型在训练集上实现了很好的训练。训练样本平均误差为3.51%，检测样本为5.95%，极差相差较大，训练样本集为17.238%，检测样本集为13.549%，表明模型对奇异值的抗干扰能力较弱，但算法整体预测效果较好。

ELM和RF模型验证流程同上。ELM在训练集上平均方法的相对误差为0.7%，在检测集为1.3%。极差在训练与检测分别为4.2%和8.2%。通过对比可以发现模型在训练集上的结果表现较好，但在检测集上较差，说明网络模型泛化能力较差。使用随机森林模型对数据进行训练，设置子节点数为5，最大深度为200，基尼系数设为0.938 8。训练集与检测集的回归误差值均在100以内。训练集的相对误差在 [﹣0.1，0.1]，验证集在[﹣0.05，0.1]，表明模型在训练集与验证集上的表现相差不大。平均误差在训练集和检测集上分别为3.812%和4.256%，极差分别为16.024%和15.894%。也证明模型在训练接与验证集上都能得到较好的检测效果。通过对比SVM+GA和极限学习机模型可以发现，随机森林的平均相对误差大于SVM和ELM，但是极差小于SVM和ELM，整体预测效果较弱，但是对奇异值的抗干扰能力较强。

集成学习算法模型：本文将SVM、ELM和BF进行集成使用，使得模型可以自适应地针对多种数据作出更加准确的回归。集成学习模型检测集上训练测试结果如图1所示，训练样本的误差在20之内，相对误差字在0.005以内，远小于单独使用当个学习器的误差。在检测集上，误差值也在20之内，相对误差也0.005以内，表明集成学习算法无论是在训练集还是检测集上，都具有更小的误差。

集成学习模型在训练集和检测集上的绝对误差与相对误差的最大值、最小值、平均值、标准差和极差如表2所示，训练集的平均相对误差为0.49%，检测集为0.194。在训练集上的极差为4.55%，检测集为4.277 7%。无论是平均误差、极差、标准方差都远小于单独使用三种学习器，表明了集成学习算法具有最好预测能力。在其他三种模型中，平均误差最小的是SVM，其次为极限学习机，最差的是随机森林，但随机森林具有最小的极差。集成学习集合了三种模型的优势，既能降低平均误差，又能避免极差大导致奇异值造成的干扰。

集成学习模型在正常功率的预测回归上取得了很好的效果，同样在限功率的回归预测中，也取得了很大的成功，误差和相对误差都很小。训练集和检测集的表现没有很大差别，说明模型具有很好的泛化性。

集成学习模型在限功率训练集上平均值的相对误差为0.1451%，检测集为0.227%，极差训练集为7.81%，检测集为6.363%。可以发现模型不仅在训练集上取得了很好的效果，在检测集上表现也比较出色，这证明了集成学习模型具有良好的鲁棒性。

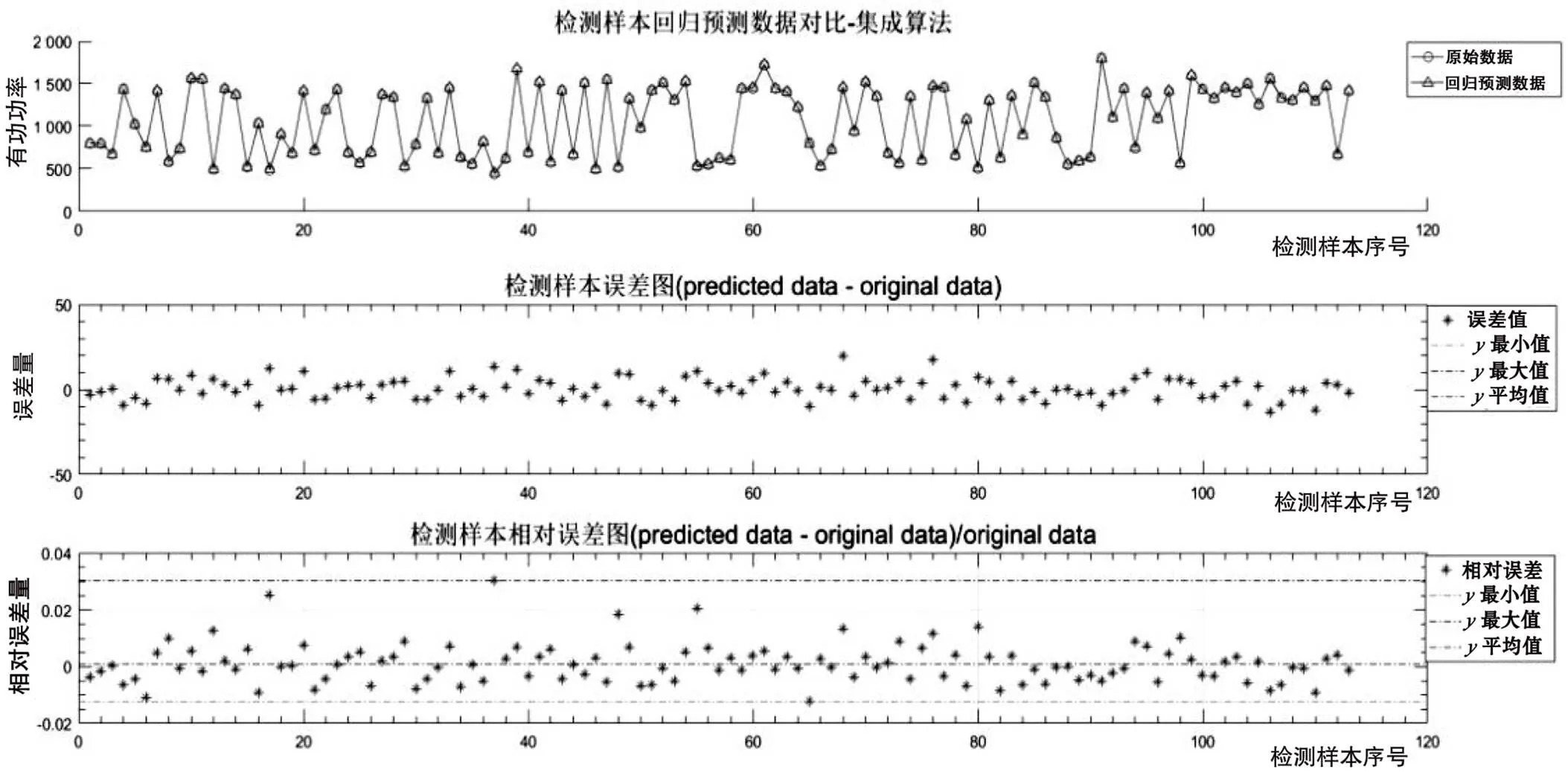
图1 集成学习检测样本测试结果

表2 集成学习综合输出结果

集成学习算法 训练检测 绝对误差相对误差/（%）绝对误差相对误差/（%） 最小值﹣15.371.244﹣13.181.246 最大值15.633.30719.383.031 平均值﹣0.057 630.490 50.334 40.194 7 标准方差6.1220.639 76.2860.706 6 极差314.5532.564.277

4 结语

本文针对风电场SCADA历史数据的数据特性，利用随机森林算法对样本数据进行分类预测，以提高分类预测准确率。同时利用平均准确率减少的重要性评估对输入参数的属性重要度进行计算，对输入因素实现降维的同时得出各重要因素的权重值并给出决策表。然后利用SVM、ELM和RF组成集成模型，运用正常功率数据进行实验对比，SVM的平均误差最小但极差较大，RF的平均准确率较低但极差小，可避免奇异点的影响，ELM介于两者之间。本文构建的集成学习算法综合了三种学习器的优点，精度远远优于单独使用每个学习模型。最后，将模型应用于限功率数据集进行检测，也取得了很好的效果，也证明了本文提出的集成学习模型具有很好的泛化性和适应性。

［1］钱政，裴岩，曹利宵，等.风电功率预测方法综述［J］.高电压技术，2016，42（4）：1047-1060.

［2］薛禹胜，雷兴，薛峰，等.关于风电不确定性对电力系统影响的评述［J］.中国电机工程学报，2014，34（29）：5029-5040.

［3］刘强，胡志强，周宇，等.基于CEEMD和随机森林算法的短期风电功率预测［J］.智慧电力，2019（6）：71-76.

［4］LIU H，MI X，LI Y.Smart multi-step deep learning model for wind speed forecasting based on variational mode decomposition，singular spectrum analysis，LSTM network and ELM［J］.Energy Conversion & Management，2018（159）：54-64.

［5］李军，闫佳佳.基于KELM-AdaBoost方法的短期风电功率预测（英文）［J］.控制工程，2019（3）：492-501.

［6］刘爱国，薛云涛，胡江鹭，等.基于GA优化SVM的风电功率的超短期预测［J］.电力系统保护与控制，2015（2）：90-95.

［7］WU W Z，CHEN K J，QIAO Y，et al.Probabilistic short-term wind power forecasting based on deep neural networks［J］.IEEE Probabilistic Methods Applied to Power Systems，2016（12）：1-7.

［8］南晓强.风功率预测技术水平分析及改进措施研究［J］.山西电力，2019，214（1）：3-7.

［9］朱乔木，李弘毅，王子琪，等.基于长短期记忆网络的风电场发电功率超短期预测［J］.电网技术，2017，41（12）：3797-3802.

TM614

A

10.15913/j.cnki.kjycx.2020.14.003

2095－6835（2020）14－0010－03

葛滨（1993—），男，硕士研究生，研究方向为感知互联与协同计算。

〔编辑：王霞〕