基于小波理论的混凝土坝变形PCA-IPSO-SVM预测模型

柳志坤，周兰庭

(河海大学水利水电学院，南京 210098)

0 引 言

混凝土坝变形监测数据能直观可靠地反映大坝的运行状况，监测序列是一种随时间变化的数据信号，主要受到水压、温度和时效的影响，二者之间是一种非线性映射的关系，加之监测过程中常带有一定的系统噪声和观测噪声，往往会掩盖实际变形值，这使得变形监测序列具有较强的非线性和不确定性，增加了资料分析的困难度。目前常采用的监控模型主要有统计型、混合型、确定型及其衍生的各种改进模型，随着智能算法的发展，遗传算法(GA)、神经网络(BP)、支持向量机(SVM)等均被应用到大坝安全监控中。在处理大坝变形监测数据这类高维数、非线性的问题上，SVM是一种较为理想的模型，钱秋培等[1]应用SVM建立了混凝土坝变形监控模型，论证了其短期预测能力优于长期预测能力，合理选择测试集数目对模型预测影响明显；孙小冉等[2]将粗集理论与SVM结合，简化了大坝变形影响因素和效应量之间的映射关系，优化了模型输入使模型更能体现大坝的运行机制；赵二峰等[3]基于结构风险最小化原则和提升算法强化学习的思想，提出一种稳定性好的AdaBoost-SVM变形预测模型，增强了模型的泛化能力和预测精度；杜传阳等[4]利用马尔科夫链(MC)对原始数据的残差进行处理，并基于SVM理论建立大坝变形监测模型；黄梦婧等[5]利用差分自回归移动平均模型(ARIMA)来处理非平稳时间序列，对SVM模型的残差进行处理，改进了原有大坝变形监控模型；张海龙等[6]将极限学习机(ELM)用于混凝土坝变形监控模型的构建中，并通过改进粒子群算法进行参数寻优，提高了模型的学习能力；针对大坝变形影响因子繁多，因子之间关联性强的问题，陈斯煜等[7]利用主成分分析(PCA)对监测数据降维，将提取的主元影响量作为径向基神经网络(RBF)的输入量，建立了混凝土坝位移趋势性预测模型。本文在前述研究的基础上，通过对实测数据进行去噪，并利用主成分分析提取影响因子的主元，采用支持向量机对非线性问题进行预测，但考虑到模型参数的合理选择对预测精度有较大的影响，本文利用粒子群算法的全局搜索能力及鲁棒性强的特点，采用改进的粒子群算法对模型参数进行寻优，建立了基于PCA-IPSO-SVM的组合预测模型。

1 理论方法

1.1 小波理论

小波分析理论[8,9]是在Fourier的基础上发展起来的一种时频分析方法，克服了传统变换的缺点，通过小波基函数的伸缩变换实现对信号的多尺度分析，大坝变形监测数据就是一个时间序列，小波理论凭借良好的时频局部化和多分辨率分析的能力，在大坝监测数据处理领域得到广泛应用。

大坝变形监测数据为一离散的时间序列，故在应用小波理论时采用其离散形式：

(1)

式中：f(t)为变形时间序列；φ*为小波基函数的复共轭；a0、b0均为实常数；j、k为整数。

小波分析的实质是对信号根据尺度大小由粗到细地分解，不断地将低频信号进一步分解为低频和高频信号，分解N层后即可得到N个高频信号和1个低频信号，进而实现把信号分解为任意频率上的高频和低频。

大坝变形监测序列本身包含着大坝实际运行状态的信息，但在监测过程中往往受到环境、仪器等因素的影响，序列中的噪声会给建模分析带来一定的偏差，故将监测序列视为一维信号进行去噪处理，以提高数据分析的精度。小波去噪的关键在于控制阈值的选取，阈值过小会保留过多噪声，阈值过大则会产生失真现象，此处采用使最大风险最小化的极大极小值阈值法来确定阈值，公式如下：

λ=σ(0.393 6+0.182 9log2n)

(2)

σ=median(|ωj|)/0.674 5

(3)

式中：σ为标准差；n为数据个数；median(|ωj|)为小波系数绝对值中值。

选定阈值后，采用式(4)的软阈值法去噪，当小波系数的绝对值大于或等于阈值时，将两者相减，符号保持不变；而小于阈值时直接置为零，最后对小波系数重构可得去噪后的监测数据。

(4)

式中：λ为阈值；ω为小波系数；ωλ为阈值处理后的小波系数。

1.2 主成分分析(PCA)

在建立混凝土坝变形的预测模型时，需要将与变形相关的各影响因子作为模型的输入量，但因子数量繁多且因子间相互关联性复杂，不仅降低模型的精度还增加了运算时间。因此，借助主成分分析法[10,11]提取主要因素作为模型的输入量，将原始高维数据转化成低维数据，消除原数据间的相关性，并能在最大程度上反映原数据包含的信息。

设大坝变形预测模型有p个影响因子，每个因子有n个监测数据，则数据集X：

(5)

式中：xi=(x1i,x2i,…,xni),i=1,2,…,p。在对变形影响因子进行主成分分析时，按式(6)～(8)对数据集进行标准化处理，并按式(9)计算相关系数矩阵。

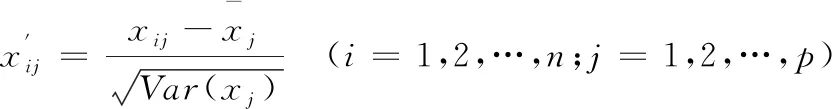
(6)

(7)

(8)

(9)

最后根据特征方程求出各特征值和对应的特征向量，并将特征值从大到小排列，此即主成分的排序，根据式(10)、(11)计算各主成分的贡献率和累计贡献率，并选取累计贡献率大于85%的主成分作为最终的主元来代替原始数据。

(10)

(11)

式中：λi为特征值；γi为各主成分贡献率；Mk为主成分累计贡献率。

1.3 改进的粒子群算法(IPSO)

粒子群算法[12,13]最早起源于群鸟觅食的现象，算法中的每一个粒子代表优化问题的一个可能解，并通过速度和位置两个指标来刻画粒子的行为，粒子的优劣通过适应度值来判断，而适应度函数则根据具体情况而定，粒子在寻优中通过分析个体极值和群体极值的情况决定是否更新，通过不断迭代搜寻到全局最优解。

设在一个N维搜索空间中，群体粒子数为m，第i个粒子的位置为xi=(xi1,xi2,…,xin)，速度为vi=(vi1,vi2,…,vin)，个体极值为pi=(pi1,pi2,…,pin)，群体极值为gi=(gi1,gi2,…,gin)，则经过k次迭代后PSO算法按下述公式对粒子的位置和速度进行更新：

vidk=ωvidk-1+c1r1(pidk-1-xidk-1)+c2r2(gidk-1-xidk-1)

(12)

xidk=xidk-1+vidk

(13)

式中：i=1,2,…,m，d=1,2,…,n，c1、c2为加速常数；r1和r2是[0，1]内的随机数；ω为惯性权重。

粒子群算法中最需要关注的参数是惯性权重ω，这直接关系到算法寻优的效果，ω越大其全局寻优能力越强，局部寻优能力较弱；ω越小其局部寻优能力越强，全局寻优能力较弱。在标准粒子群算法中，ω常取为1，但考虑到实际寻优中，算法在不同时期对全局和局部寻优的需求程度不同，ω不能一成不变，此处规定其初值为0.9，终值为0.4，采用式(14)的线性递减惯性权重来控制ω的大小，对粒子群算法进行改进，使算法在前期加强全局寻优，后期注重局部寻优。

ω(k)=ωs-(ωs-ωe)(T-k)/T

(14)

式中：ωs为权重初值；ωe为权重终值；T为最大迭代次数；k为当前迭代次数。

1.4 支持向量机(SVM)

支持向量机[14,15]源于模式分类研究，后推广至回归问题，通过选定的非线性映射函数将输入量转化到高维空间中，并在该空间中构造最优决策函数，它基于结构风险最小化准则，并具有全局最优性和较好的泛化能力，对于大坝变形序列这种复杂的非线性问题，采用该方法能取得较为理想的结果。

给定样本数据(xi,yi)，i=1,2,…,n，xi∈Rm，yi∈R。采用非线性映射φ(x)将数据映射到高维空间中，并构造线性拟合函数f(x)=ωφ(x)+b，其中ω为权值向量，b为常数。基于结构风险最小化原则求解ω和b，寻优过程等价于下式：

(15)

式中：C为惩罚因子；ξ为松弛变量。

对上述问题建立拉格朗日函数求解：

L(ω,b,ξ,α)=

(16)

式中：αi为拉格朗日乘子。根据KKT条件可求得：

(17)

消去ω和ξi，核函数K(x,xi)取为高斯径向基函数(RBF)，通过求解方程组最终得到支持向量机的回归方程，分别见式(18)、(19)。

(18)

(19)

1.5 组合预测模型

根据1.1～1.4的理论分析，基于小波理论的混凝土坝变形PCA-IPSO-SVM预测模型建模步骤如下，流程图见图1。

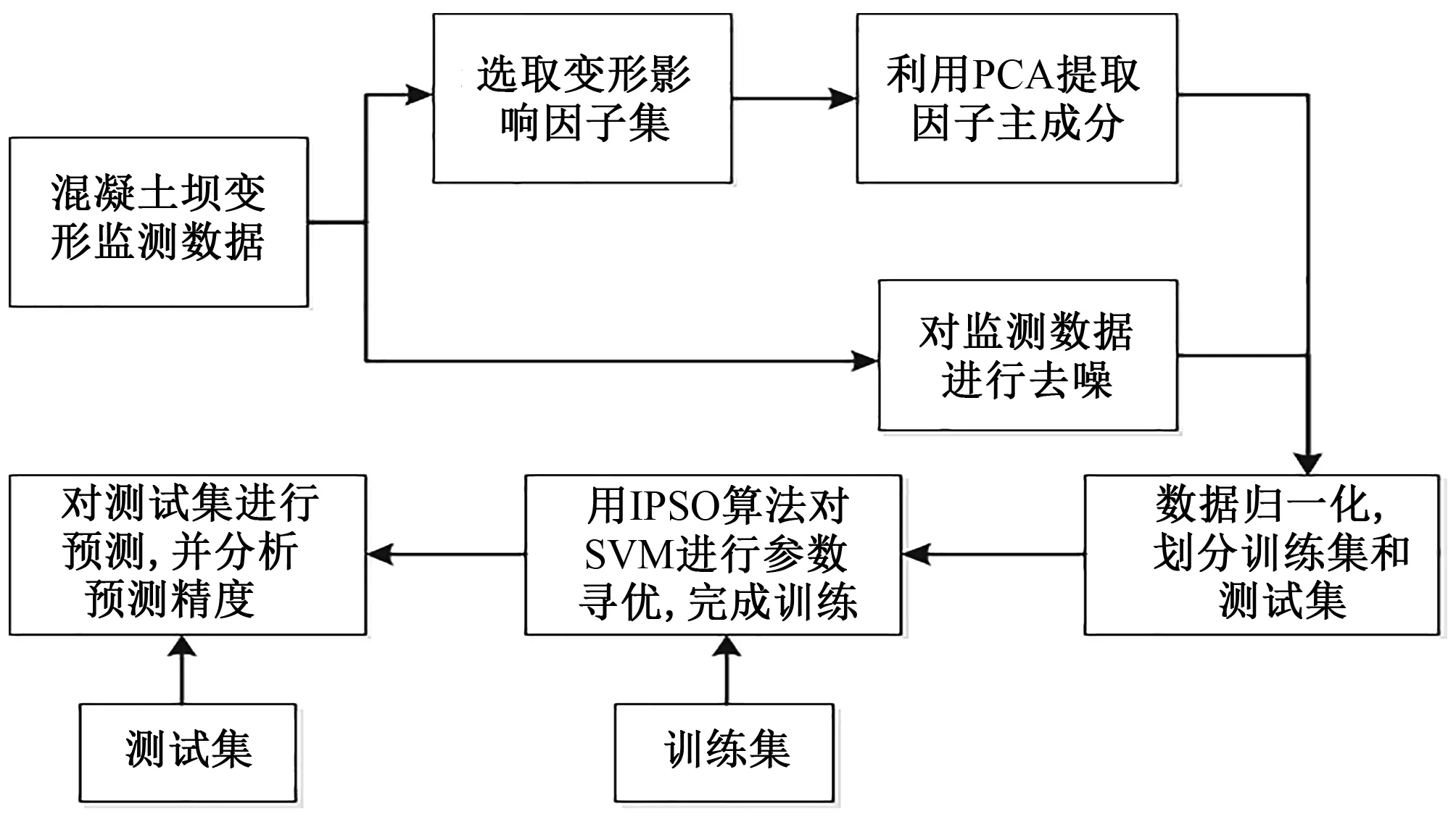
图1 建模流程图

(1)对混凝土坝变形监测序列Y采用极大极小值的软阈值法进行去噪处理，记去噪后序列为Y1；

(2)根据影响大坝变形的水压、温度、时效三大主因素以及大坝安全监控统计模型选取适当的影响因子，记为D1,D2,…,Dn；

(3)对(2)中选取的影响因子进行主成分分析，并提取累计贡献率大于85%的因子作为主成分，记为Z1,Z2,…,Zm；

(4)将主成分序列进行归一化处理，并相应的划分训练集和测试集。将主成分作为SVM的输入量，将去噪后序列作为SVM输出量；

(5)采用IPSO算法对SVM的参数进行寻优，求解最优的C、σ值，并代回SVM中，完成模型训练；

(6)用训练好的模型对测试集进行预测，并分析预测精度。

2 工程实例

某水电站由拦河大坝、坝后溢流式厂房、埋设于坝内的输水系统、泄水底孔及过木筏等组成，大坝类型为混凝土重力坝，坝顶高程280 m，最大坝高78 m，坝顶全长253 m，本文为分析其位移变化情况，选取该坝的9号坝段引张线测点EX7自2012年12月6日至2013年12月26日的监测数据为样本，样本实测位移和上游水位过程线如图2所示，其中以2012年12月6日至2013年12月6日的数据为训练集，以2013年12月7日至2013年12月26日的数据为测试集。

图2 EX7测点实测位移及上游水位过程线

2.1 数据预处理

在实际位移的监测过程中，由于噪声等因素的影响，实测位移数据往往存在一定的偏差，从而影响建模分析，故对图2中的实测位移运用小波原理进行去噪处理，以增加数据的真实度。首先，使用正则性较好的db4小波对原始监测数据进行分解，分解层数为4，分解之后的低频序列和高频序列见图3，高频序列为d1、d2、d3、d4，低频序列为a4。从图3中可以看出由于噪声的存在使得高频序列波动较为剧烈，因此有必要采用软阈值法进行去噪处理。

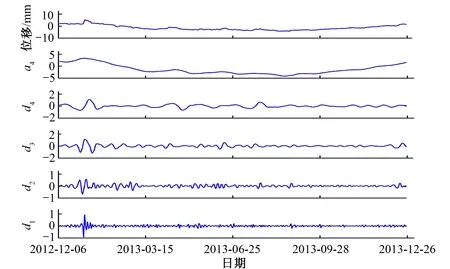
图3 小波分解过程线

然后通过调用matlab函数库中的wnoisest函数，提取第一层的细节系数来估计噪声的标准偏差，通过“极大极小值阈值法”确定阈值，并采用全局阈值处理，即对近似系数不做处理而对细节系数进行处理，最后将处理后的数据进行重构，得到去噪后的变形序列如图4所示，由图4可以看出去噪后的数据相对光滑，利于下文建模分析。

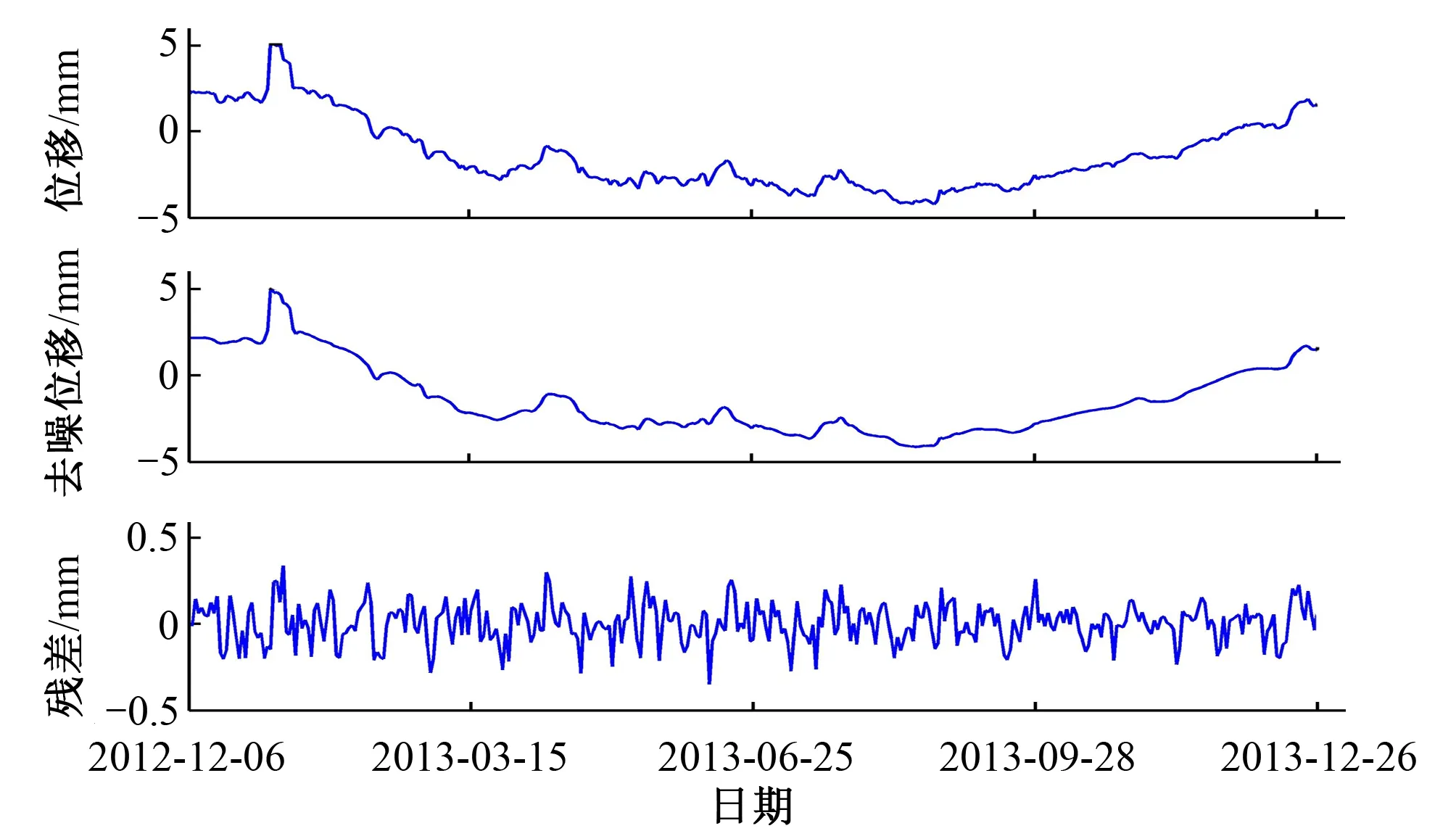
图4 去噪前后数据过程线

2.2 建模分析

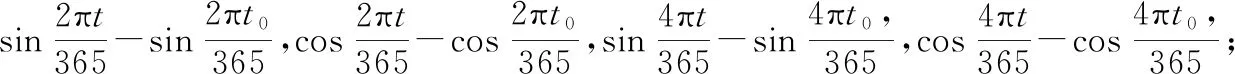
运用SPSS对上述9个影响因子进行主成分分析，得到其特征值及方差贡献率如表1所示。

表1 影响因子贡献率表

由表1可知，前4个主成分的累计贡献率为94.425%，可以反映原数据的大部分信息，故选择前四个主成分作为模型的输入向量，并得到前4个主成分的评分系数，如表2所示。由式(20)计算主成分，并将归一化后的数据作为模型输入变量。

表2 主成分评分系数

Fi=mi1Y1+mi2Y2+mi3Y3+mi4Y4+

mi5Y5+mi6Y6+mi7Y7+mi8Y8+Mi9Y9

(20)

式中：Fi为主成分(i=1,2,3,4)；Y1～Y9为变形影响因子；mi1～mi9为对应的各主成分的评分系数。

基于选定的样本数据，划分训练集和测试机，并利用IPSO算法对SVM的参数C和σ进行寻优。设定粒子个数为20，种群迭代次数为200，C的范围为[0.1,100]，σ的范围为[0.01,10]，加速常数c1、c2为1.2，惯性权重采用式(14)的确定方式，适应度函数为SVM输出值与样本实测值的均方误差。

由图5可以看出，IPSO-SVM模型的最佳适应度要优于未改进模型的最佳适应度，改进后的最佳适应度稳定在0.013附近，此时C=38.398，σ=0.29。将划分好的训练集主成分输入到SVM中进行学习，将测试集主成分输入到已训练好的预报模型里，分别得到拟合和预测结果，并与单一SVM模型和BP神经网络的拟合和预测结果进行对比，各模型拟合和预测曲线见图6、图7。

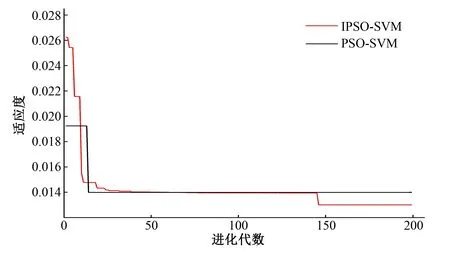
图5 改进前后适应度比较曲线

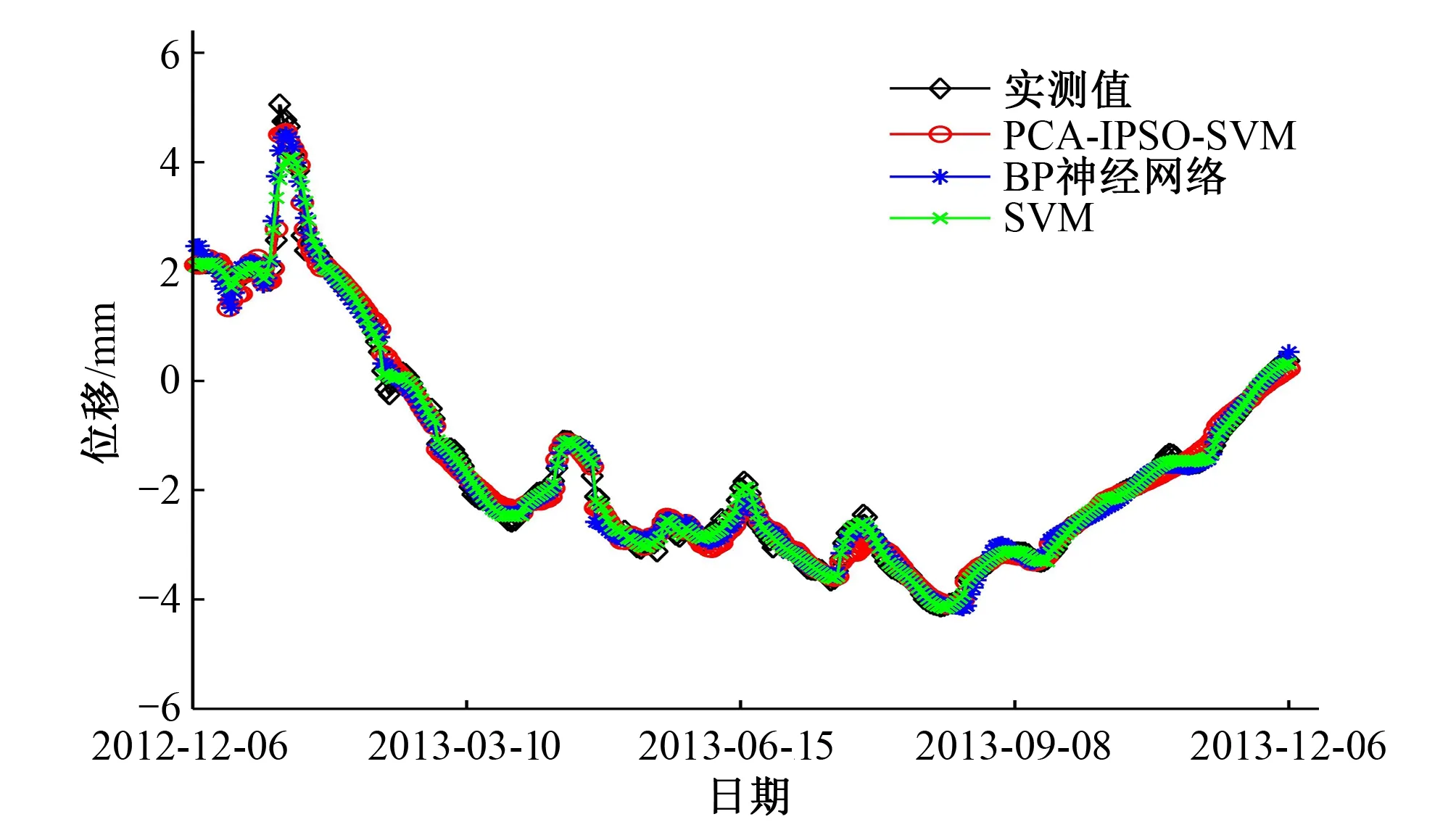
图6 各模型拟合曲线

图7 各模型预测曲线

根据预测结果，基于均方根误差(RMSE)、平均绝对百分比误差(MAPE)和平均绝对误差(MAE)三项统计指标定量比较各模型的预测精度，计算公式如下，计算结果如表3所示。

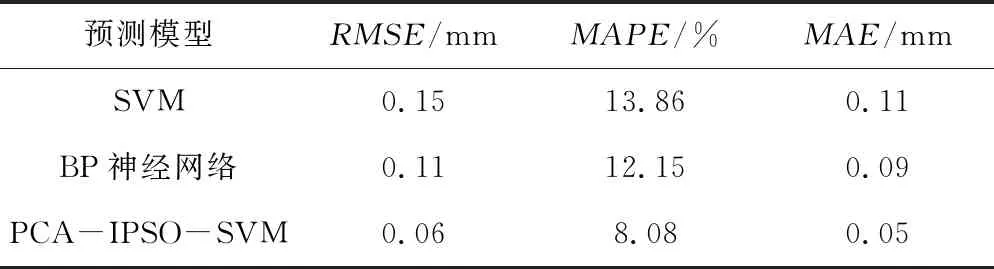
表3 各模型预测精度

(21)

(22)

(23)

从表3可以直观发现，相比于单一的SVM模型和BP神经网络，本文提出的PCA-IPSO-SVM模型的预测精度较高，三项误差指标均较小。由于影响混凝土坝变形的各个因素之前往往具有较强的非线性，因此本文提出的模型在混凝土坝变形预测方面有着较强的合理性和优越性。

3 结 论

本文充分考虑实际中混凝土坝变形序列的非线性特征及含噪特性，基于复合建模思想将小波理论、粒子群算法、主成分分析和支持向量机应用到大坝变形预测中，该方法在消除监测噪声影响的同时也降低了因子之间的关联性对预测精度的影响，并采用IPSO算法对SVM的参数进行寻优，减少其陷入局部最优的概率，提高了预测精度，弥补了传统方法数据分析量大、精度欠佳的缺点。工程实例表明，本文提出的方法能较好地进行混凝土坝变形预测，相较于传统的预测模型，具有更高的实用价值。