改进小波阈值函数在水电机组振动信号降噪中的应用

安周鹏，肖志怀，章品勋，吴景辉，廖文亮，仝建伟

(1.国网新源浙江缙云抽水蓄能有限责任公司,浙江 缙云 321400；2.武汉大学动力与机械学院,武汉 430072)

在水电机组的状态监测和故障诊断中，通常需要对采集到的信号进行分析处理，才能提取到信号的真实特征信息，由于水电机组所处的环境和其本身的运行特性，决定了所采集到的信号往往含有大量的噪声信号，因此首先必须要对采集的信号进行降噪，再提取信号特征。相关研究表明：大约80%的机组故障都在振动信号中有所反映[1]，因此监测和诊断水电机组的振动信号，及时发现和排除故障，对水电厂机组的安全稳定运行极其重要。

信号降噪的传统方法是基于傅立叶变换的降噪方法。傅里叶变换(DFT)将时域信号转换到频域，是一种全局的信号处理方法，清楚展现信号所包含的各种频率[2]，具有低通性，平滑信号突变点等特点，而水电机组非平稳的振动信号所包含的振动信息是突变的和局部的，傅里叶变换对非平稳信号具有很大的局限性；为了解信号的局部信息，Gabor于1946年提出了窗口傅里叶变换(STFT)，窗口傅立叶变换由于加了固定的窗函数可以反映信号的局部特征，但是窗函数的固定,不可避免存在频谱泄露而产生失真现象[3]，因此窗口傅里叶变换不能自适应信号的变化[4]；小波变换(DWT)是一种时-频联合分析方法，在时间域和频率域都有良好的局部分辨率，其将信号分解到尺度和时间的相平面上，且尺度和时移参数对信号的突变具有自适应性，因此小波非常适合分析水电机组非平稳信号。

小波降噪方法有很多种，其中以D.L Donoho在小波变换的基础上提出的小波阈值函数去噪算法最为常用[5]，在信号降噪中表现出一定的优势，但传统的软、硬阈值函数存在着的不足之处，硬阈值函数去噪后的信号出现突变不连续现象，发生局部的振荡[6]；软阈值函数去噪后的重构信号精度不及原始信号。因此本文提出一种改进的阈值函数，经过仿真信号的验证表明其降噪效果好，可大幅提高信噪比，并降低均方根误差；经过电厂采集的振动信号验证表明其能更好的保留振动信号的能量，并将高频噪声干扰消除，降噪效果优于经典阈值函数。

1 小波阈值降噪的原理

1.1 小波变换原理

对于实际信号f(t)∈L2，在小波变换中都可以按分辨率和有限精度来分解，即：

(1)

式中：φ(t)为尺度函数；V(j,k)为低频空间的尺度系数；U(j,k)为高频空间的小波系数；φ(t)为尺度函数；ψ(t)为小波函数。

多尺度分析基于小波分析产生，其变换特性可逆、算法快速且具有高阶消失矩，因此在实际应用中，常用在小波离散多尺度分析基础上形成的Mallat算法对信号进行小波分解。

V(j+1,k)=V(j,k)⊗h(j,k)

U(j+1,k)=U(j,k)⊗g(j,k)

(2)

式中：h和g分别是多尺度分析对应的低通和高通滤波器；V(0,k)为原始信号f(k)，相应的去噪后的小波逆变换重构公式为：

(3)

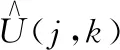
1.2 小波阈值去噪

设采集的含噪离散信号为：

f(t)=s(t)+n(t)

(4)

式中：s(t)为原信号；n(t)是服从N(0,σ2)分布的Gaussian白噪声。其小波阈值函数除噪的具体步骤如下：

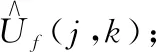
SNR的定义为[1]：

(5)

MSE的定义为：

(6)

2 改进的阈值函数及阈值选择

经典的硬、软阈值函数表达式如下：

硬阈值函数(hard Threshold Function)：

(7)

软阈值函数(Soft Threshold Function)：

(8)

式中：λ为阈值，sign(*)为符号函数，即：

(9)

硬、软阈值函数降噪算法的原理是，利用Mallat算法将信号分解后，把分解的小波系数绝对值小于阈值的点置0，而大于阈值的点不变或者收缩[8]。在实际应用中表明，经典阈值函数都有一定的降噪效果，算法简单，但是硬阈值函数降噪后存在着局部震荡[9],重构信号不如原信号光滑，软阈值函数降噪后重构的信号与原信号之间存在着恒定的偏差，重构信号的精度受到影响[10]。本文提出了一种改进的阈值函数同时克服经典阈值函数降噪的缺点，其表达式如下：

(10)

其中a=2，m=5,阈值λ通常采用固定阈值方法计算[11]：

(11)

式中：N为采样信号的长度；σ为噪声标准差，实际应用中σ是未知的，需要进行估计，利用小波系数估计噪声标准差σ[12]：

(12)

式中：Median |x|为小波高频系数的中值。3种阈值函数示意如图1。

图1 各阈值函数示意图

3 验证与分析

采用仿真信号和电厂采集信号分别进行不同阈值函数下的去噪实验，以对比检验各阈值函数的降噪效果。

(1)Heavy sine信号：选择固定阈值及db4小波函数分解3层，分别采用软、硬阈值函数和改进的阈值函数对Matlab中Heavy sine信号,加SNR=20的噪声，然后降噪，如图2所示，降噪后的信噪比及均方根误差见表1。

图2 各阈值函数对Heavy sine信号的去噪图

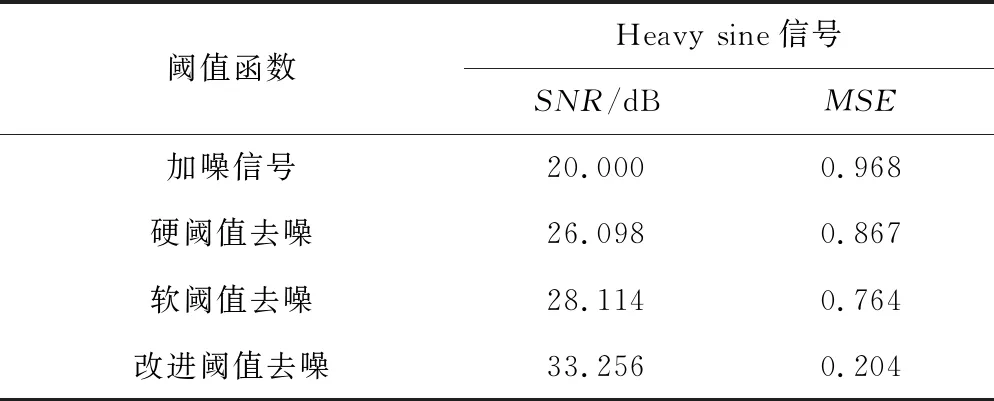
表1 Bumps和Heavy sine信号的SNR和MSE对比表

从图2和表1可得出：经典阈值函数都有一定的去噪效果，硬阈值函数去噪后的波形存在振荡，连续性不及原信号，软阈值函数去噪效果要好于硬阈值函数去噪，但此两者的均方根误差都较大，说明重构信号相比原信号误差较大，而改进的阈值函数去噪后重构信号更接近于原始信号，不仅信噪比提高较大，均方根误差也有大幅减小。

(2)实测信号：某抽水蓄能电厂机组为立式，额定转速为500 r/min，在一次大修后的调试过程中，发现一台机组振动较为严重。振动传感器的采样频率为250 Hz，采集到的信号及各阈值函数降噪后的效果如图3所示,依然采用固定阈值和db4小波函数对采集信号进行3层分解。

从图3可知，硬阈值函数去噪后存在局部突变和连续性不及原信号的问题，软阈值函数去噪相比原信号振幅降低，波形存在恒定偏差,而改进阈值函数不仅除掉了噪声，而且波形更加接近于采集信号[10]。

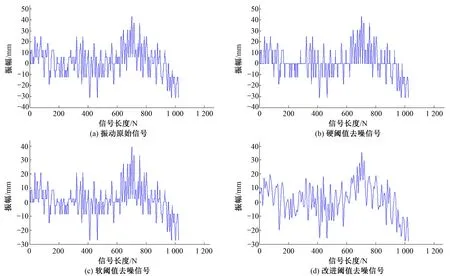
图3 振动信号的去噪效果图

从电厂采集的振动信号，没有办法得到原始无噪声信号，其降噪效果无法用性噪比和均方根误差衡量[13]。将信号分解后，其时频域内的所有故障信息就包含在了各频段信号的能量特征中[12]，因此本文衡量去噪效果标准是对振动特征的能量保留。先计算各频段内的信号能量，再将各频段的能量进行归一化处理，就得到了反映故障信号的能量特征[10]，各频带的能量计算公式见文献[14]。

从机组的额定转速可知其转频为fn=8.33 Hz。根据奈奎斯特定理，采样频率为fs=250 Hz时分析数据的上限频率为125 Hz。小波分解三层后的各频段的频率范围见表2。

表2 三层小波分解后各频段频率范围

由机械不平衡引起的振动特征频率主要是转频和多倍频[15]。图4-图7是采集信号和各方法降噪信号能量谱，表3是其相应各频带的能量对比，从各能量谱中看出振动特征能量主要存在于频带1和频带2，而根据采集信号的特点其1倍频、2倍频都在频带1中，3倍频在频带2中，这也符合振动特征信号的能量分布。与采集信号相比，经典阈值函数降噪后频带1的能量都有所减弱，频带2的能量有所增强，但两种方法没有完全消除高频干扰；而改进的阈值函数降噪极大增强了有振动特征频带，同时消除了高频噪声干扰。因此改进阈值函数降噪与软、硬阈值函数相比，不仅很好的保存了振动特征的能量，而且将高频噪声干扰消除，是一种优于传统小波函数的降噪方法。

表3 几种阈值函数降噪后能量比较

图4 采集信号能量谱图图

图5 硬阈值函数降噪能量谱图

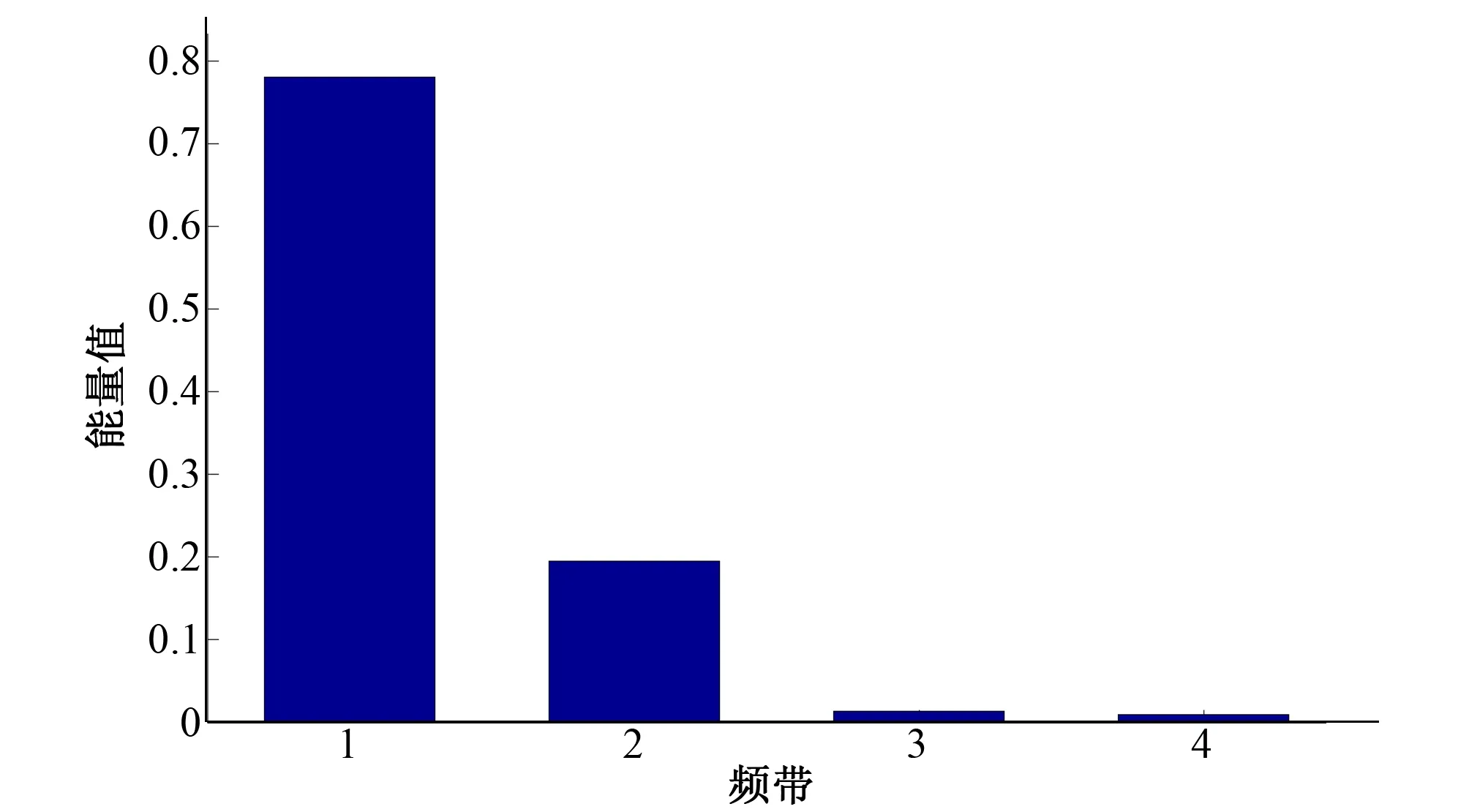
图6 软阈值函数降噪能量谱图图

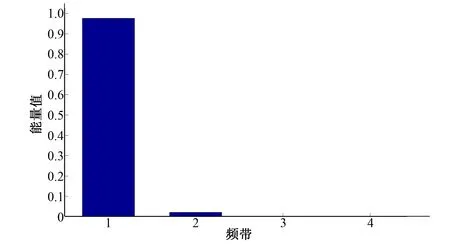
图7 改进阈值函数去噪能量谱图

4 结 语

信号降噪对于准确的提取振动信号的特征极为重要，Donoho在小波基础上提出的经典阈值函数降噪算法有一定的去噪效果，但是各自存在一些不足之处，本文在分析了传统函数降噪的缺点之后，提出了一种改进小波阈值函数算法，经过仿真信号的验证表明其克服了经典阈值函数的缺点，可以大幅提高信噪比，并降低均方根误差，降噪效果好；经过电厂实际采集振动信号的验证表明其降噪效果是优于经典阈值函数，对振动特征能量保存好，更有利于故障特征提取，拥有较好的实用性。