基于先导发展法的绝缘子串伏秒特性研究

马博翔

(国网北京市电力公司电缆分公司，北京 100022)

伏秒特性曲线是指在冲击电压波形不变的情况下，绝缘的冲击放电电压幅值与相应的放电时间的关系曲线。对于持续作用的直流或工频电压来说，绝缘的击穿电压一般有1个确定值，但对于脉冲性质的电压，气隙的击穿电压与电压波形(即作用的时间)有关。对输电线路的绝缘子而言，其承受的各种雷电和操作过电压均为持续时间短的冲击电压，绝缘子串的击穿电压与电压作用时间有紧密的联系，因此绝缘子串伏秒特性曲线研究对于输电线路防雷保护和电力设备的绝缘配合设计具有十分重要的意义[1-5]。

目前输电线路绝缘子串在冲击电压下的伏秒特性曲线主要通过冲击试验获得[6-9]，但输电线路绝缘子型号众多，相同型号的绝缘子不同串长下的伏秒特性也不一样，考虑到试验成本，无法逐个对不同型号绝缘子的伏秒特性曲线进行测量。为了更加方便地进行输电线路的防雷设计，M.Darveniza等人提出了不同串长的绝缘子在标准雷电波下的伏秒特性通用公式[10]，该公式只需统计绝缘子长度信息，方便线路运行部门进行统计分析与仿真计算，因此IEEE推荐其作为绝缘子雷电冲击闪络电压的计算公式[11]，但由于此公式是在标准雷电波的情况下得到的，其在绝缘子串上施加非标准雷电波情况下得到的伏秒特性的正确性还有待研究。

因此，本文提出了1种基于先导模型发展法的绝缘子串的伏秒特性计算方法，此方法可以方便计算不同串长下绝缘子的伏秒特性曲线，并且可以考虑绝缘子串施加不同电压波形的影响。本文还将此方法计算得到的标准雷电波下的伏秒特性与试验结果进行对照，两者的差异在误差允许范围内，表明此计算方法可以较为准确地模拟绝缘子串的伏秒特性曲线。

1 绝缘子串伏秒特性的计算模型

1.1 基于先导发展法的伏秒特性计算原理

根据文献[12-13]，冲击电压下，绝缘子串闪络路径大多为沿空气闪络，并通过试验证明了绝缘子串和相同长度的棒-棒空气间隙的冲击放电行为相似，因此可以将绝缘子串的冲击闪络过程等效为相同长度的棒-棒空气间隙击穿过程。

先导发展法是一种结合长空气间隙放电的试验研究和基本理论，通过研究间隙先导发展的物理过程判断间隙闪络的计算方法[14]。先导发展法将空气间隙的放电过程分为流注、先导放电和最终跃变3个物理过程。

根据Raether-Meek判据及临界电场理论，空气间隙中的电场达到23 kV/cm时，会发生流注起始放电[15]。对空气间隙而言，当间隙绝缘上的平均电场梯度超过流注起始的临界条件时，认为流注发生起始，流注发展的时间ts可以用式(1)表示[16]

(1)

式中：E—间隙上最大电场梯度(kV/m);

E50—间隙击穿的平均场强(kV/m)。

当流注发展到一定程度后,随着外加电压的增加，流注会向先导进行转化，根据文献[17]，连续先导的起始电压可以用式(2)表示：

(2)

式中：U1c—连续先导的起始电压，kV；

D—间隙长度，m。

连续先导起始后，在间隙场强满足先导发展最低场强E0的条件下,会以速度v向前方发展。先导发展的速度v的计算公式有很多，不同的先导发展模型采用的公式均不相同[18]，本文模型中采用文献[15]提出的先导发展速度公式，如式(3)所示：

(3)

式中：v(t)—连续先导t时刻的发展速度；

k—先导速度发展系数；

U(t)—t时刻加在间隙两端的电压；

UZ(t)—t时刻剩余间隙两端的电压；

D—间隙长度；

E0—满足先导发展的最低场强。

由于先导通道电导率远高于流注，可以将先导通道视作电弧，把剩余间隙上的电压简化为外加电压U(t)减去先导通道场强产生的压降，因此可以将式(3)改写成式(4)，其中Ez为先导通道的平均场强：

(4)

当剩余间隙的场强大于先导发展的最低场强E0时，先导头部会一直向前继续发展。在间隙先导快要发展到对侧电极时，先导发展的速度会快速增加，可以认为先导的头部瞬间到达对侧极板，这个过程也被称为先导发展的最终跃变阶段。最终跃变过程与剩余间隙的长度hs有关，其中hs的表达式可以用式(5)表示[15]：

(5)

式中:D—间隙长度，m。

先导发展的时间tx可以用式(6)求得：

(6)

绝缘子串的击穿时间t为流注发展时间ts和先导发展时间tx之和，如式(7)所示：

t=ts+tx

(7)

1.2 绝缘子串伏秒特性计算流程

本模型采用双指数函数模拟不同波头下的冲击电压波形，双指数函数如式(8)所示：

u=U0ξ(e-αt-e-βt)

(8)

式中：U0—电压峰值；

a—波尾时间系数；

ξ—电压系数；

β—波头时间系数。

不同参数表示的冲击电压波形如表1所示。

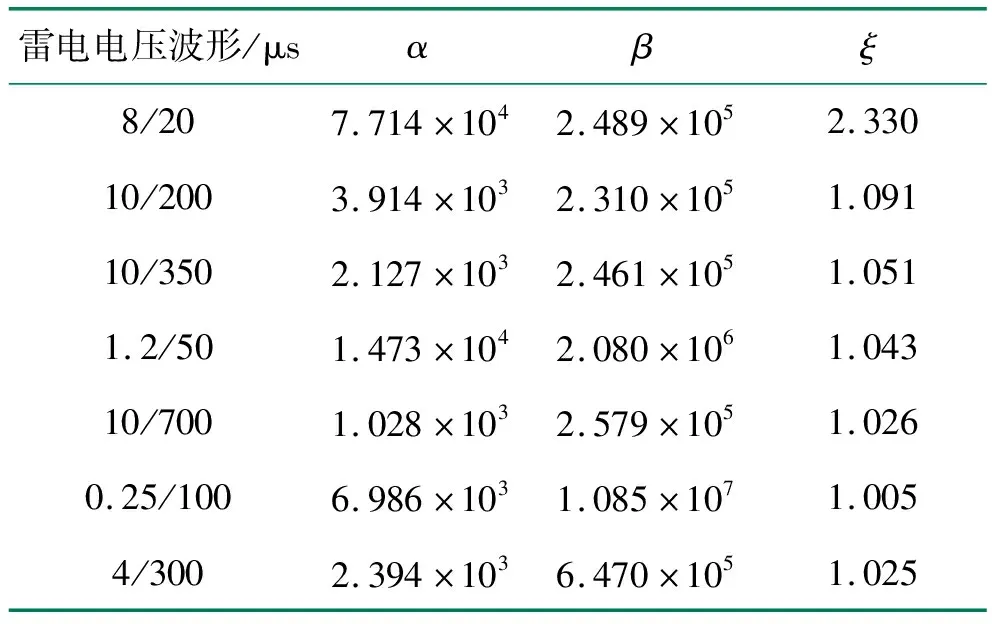
表1 不同参数下的冲击波形

在时间步长Δt较小的情况下，可以认为t+Δt时刻的先导发展长度l(t+Δt)为

l(t+Δt)=l(t)+v(t)Δt

(9)

由式(4)和式(9)可得t+Δt时刻的先导发展速度公式，如式(10)所示

(10)

由式(9)和式(10)可以得出先导在不同时刻下的先导发展长度和发展速度，当先导发展长度l(t)为D-hs时，绝缘击穿，并记录此时的击穿时间，施加固定电压下求取绝缘子串击穿时间的流程如图1所示。

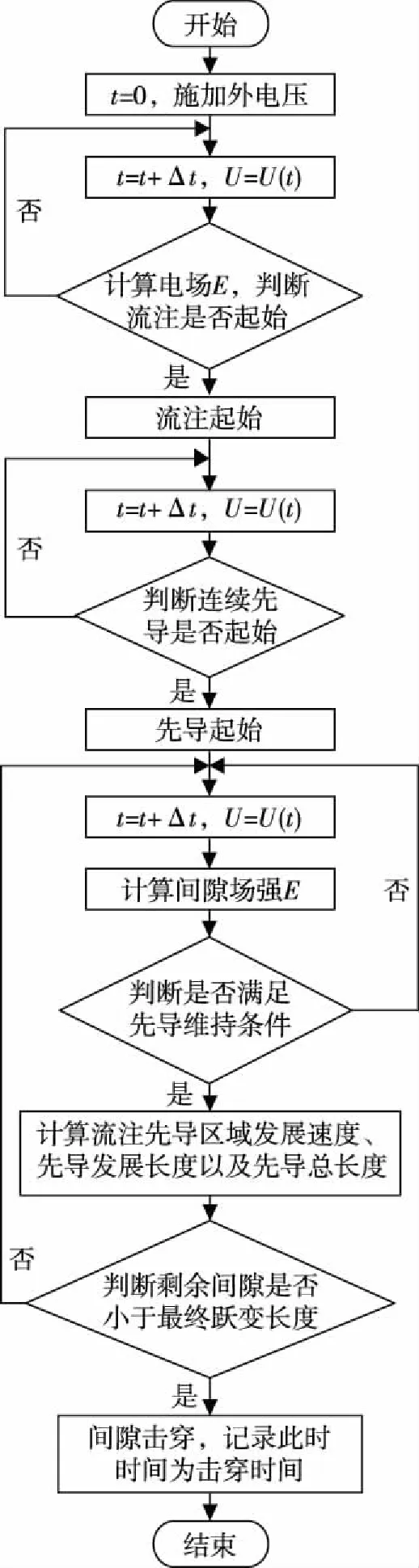
图1 求取绝缘子串击穿时间流程

仿真时，首先令绝缘子两端的电压u为初始值U0，求取绝缘子在施加电压U0情况下的击穿时间t0；然后令绝缘子两端电压U0增加ΔU(U1=U0+ΔU)，求得绝缘子在U1情况下的击穿时间t1，依次类推，可以得出绝缘子在不同电压下的击穿时间，进而得出绝缘子的伏秒特性曲线。

2 模型验证

为验证模型的正确性，根据前文建立的伏秒特性计算方法，计算25片XP-160绝缘子在波形为1.2/50 s。标准雷电波下的伏秒特性曲线，如表2所示。

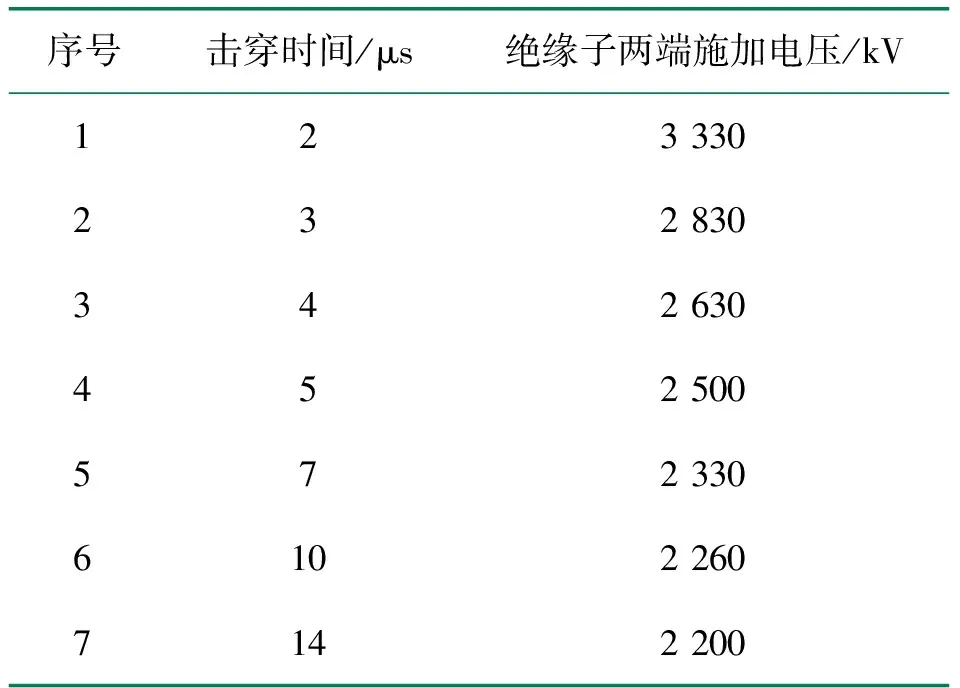
表2 25片XP-160绝缘子伏秒特性实测数值

对这些数据进行拟合，即可得到25片XP-160绝缘子的实测伏秒特性曲线表达式为

u(t)=2.168×106+1.023×106×e-t/4+

6.08×105×e-t/1.5+4.628×106×e-t/0.8

(11)

由表1可得，加在绝缘子两端的电压表达式为

u=1.043U0(e-1.473×104t-e-2.08×106t)

(12)

分别用本文的先导发展法和IEEE推荐公式法求取25片XP-160绝缘子的伏秒特性曲线，并与伏秒特性的实测数据进行比较，结果如图2所示。

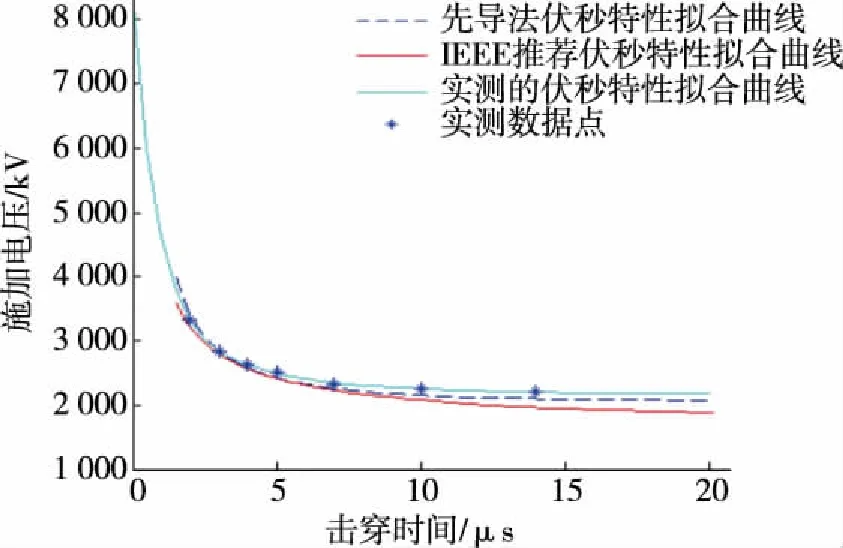
图2 不同方法求解的绝缘子串伏秒特性曲线对比

由此可见，先导法比IEEE推荐公式更加符合绝缘子的实测伏秒特性，先导法可以更为准确地模拟绝缘子串的伏秒特性曲线。

3 结 论

(1)结合长空气间隙放电过程及其闪络计算方法，考虑绝缘施加不同波头下的雷电冲击电压，建立了基于先导发展法的绝缘子串伏秒特性计算方法。通过对比，该方法计算得到的绝缘子串伏秒特性曲线相较于IEEE推荐公式计算得到的特性曲线更加逼近绝缘子串的实测特性。

(2)与IEEE推荐的伏秒特性计算方法相比，本文提出的基于先导发展法的伏秒特性计算方法因考虑了绝缘上施加电压的影响，可以用来模拟不同电压波形下绝缘子串的伏秒特性曲线。

(3)基于先导发展法的伏秒特性计算方法可较准确地模拟绝缘子串的实际放电行为，可作为模拟绝缘子串伏秒特性曲线的一种新的计算方法。