基于奇异谱分析和极限学习机的风速多步预测
董朕,殷豪,
(1.广东电网有限责任公司肇庆供电局,广东 肇庆 526000;2.广东工业大学自动化学院,广东 广州 510006)
风能作为一种可再生的环保能源,在世界能源结构中发挥着越来越重要的作用。随着整个能源网络中风能比例的增加,准确的风速预测结果对于管理人员日常配电和降低储备能力起着关键作用。为保护风电不受破坏,风速的准确预报结果也是必不可少的[1],然而,因非平稳和非线性波动,风速被认为是最难预测的天气参数之一[2]。
近几十年来,风速预报方法已经有很多种,这些方法可以分为4类:(a)物理模型;(b)统计模型;(c)空间相关模型;(d)人工智能模型。基于物理参数(如地形,温度和压力)的物理模型通常应用于长期风速预测[3]。统计模型则基于历史数据,通过建立统计方程挖掘出相应的变化趋势[4-5]。空间相关模型主要考虑不同地点风速的空间关系,在某些情况下,它可以获得更高的预测精度[6]。随着人工技术的快速发展,人工智能预测方法在风速预测领域得到广泛应用,包括人工神经网络[7],模糊逻辑方法[8],支持向量机[9]和极限学习机[10]。
此外,为减少单一模型固有的负面影响,提出了许多混合风速预测模型。为得到更高的预测精度,一些数据处理算法,如小波分解[11]、小波包分解(wavelet packet decomposition,WPD)[12]、经验模式分解[13]、集合经验模态分解(ensemble empirical mode decomposition,EEMD)[14]及快速集合经验模式分解[15]已被用于构建混合模型。这些数据分解方法可以减少原始数据的非平稳特征,间接地提高了模型的预测性能。
极限学习机(extreme learning machine,ELM)由于具有良好的预测性能而在预测领域得到广泛应用,但ELM的输入权重和隐含层偏置是随机生成的,而不是使用传统的优化方法获得,存在非最优参数的情况,故引力搜索算法[16],粒子群算法(particle swarm optimization,PSO)[17],进化算法[18]和布谷鸟搜索算法[19]等智能优化算法被广泛用于ELM的输入权值和隐含层偏置的参数优化。萤火虫算法(firefly algorithm,FA)由Yang[20]在2008年开发,是一种基于萤火虫使用荧光信号吸引其他萤火虫作为潜在伴侣行为的元启发式算法,具有自动细分,适用于高度非线性优化问题的优点,且该算法具有多模态特征,能以更快的收敛速度有效地处理多模态问题,已被广泛用于解决许多实际问题:如Mohanty[21]将FA用于管壳式换热器的设计优化,以最大限度地减少总成本,与遗传算法、粒子群算法、人造蜂群、生物地理学优化和布谷鸟搜索算法等其他方法的比较表明,FA表现出更优良的优化效果。
基于上述,提出一种基于奇异谱分析(singular spectrum analysis,SSA)和活性竞争萤火虫算法(active competitive firefly algorithm,ACFA)优化极限学习机的风速预测模型。将一种奇异谱分析的数据分解方法用于风速时间序列的分解与重构,对分解得到的序列建立极限学习机预测模型,为避免极限学习机的非最优参数问题,将一种新颖的活性竞争萤火虫算法用于极限学习机的输入权值和隐含层偏置优化,以2个不同风电场的实测风速数据为例,实验结果表明本文所提风速预测模型的精度优于其他预测模型。
1 奇异谱分析
SSA是一种新颖的结合多变量统计和概率理论的非参数方法,常被用于时间序列分析,从原始数据中识别和提取周期性,准周期和振荡分量。标准的SSA包括4个步骤,即嵌入、奇异值分解、分组和对角平均[22]。前2个步骤也称为时间序列分解,后2个则又被称为信号重构。
1.1 步骤1,嵌入
假设时间序列Y=[y1,y2,…,yN]T共有N个样本点,SSA的嵌入维度由L表示,L又称为窗口长度,令K=N-L+1,则滞后L阶的向量可被定义为
Xi=[yi,yi+1,…,yi+L-1]T,i=1,2,…,K
(1)
轨迹矩阵可定义为
1.2 步骤2,奇异值分解
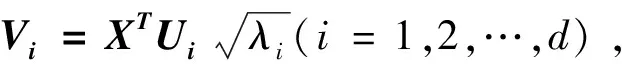
X=E1+E2+…+Ed
(3)
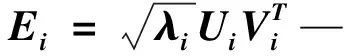
矢量V1,V2,…,Vd—其主成分;
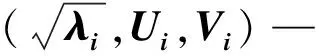
1.3 步骤3,分组
奇异值分解后,可将指数集合J=(1,…,d)分成m个不相交的组I1,I2,…,Im。将I=(i1,i2,…,ip)表示为1组指数。然后,对应于组I的合成矩阵XI可以定义为XI=Xi1+Xi2+…+Xip,此过程完成了轨迹矩阵X的后续分解。
X=XI1+XI2+…+XIm
(4)
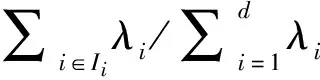
1.4 步骤4,对角平均
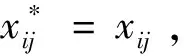
2 ACFA-ELM预测模型
2.1 活性竞争萤火虫算法
2.1.1 基本FA的位置更新算子
在FA中,每只萤火虫均被荧光强度所吸引,假设某一萤火虫有选择的向2只萤火虫中的1只飞行,则萤火虫会被亮度更高的吸引,并朝着高亮度的方向移动。荧光强度根据式(6)确定:
I(r)=I0e-γr2
(6)
式中:r—解空间中两只萤火虫间的距离;
γ—I(r)的吸收系数。
定义r=0处的萤火虫自身的荧光亮度为最大荧光亮度I0,每只萤火虫的亮度由其对应的适应度函数值来决定:
(7)
式中:Ffitness—算法寻优的目标函数,Ffitness越小,则I0越高。
萤火虫间的吸引度β则是通过式(8)计算:
β=β0e-γr2
(8)
式中:β0—距离为0时的吸引度。
2个萤火虫Xi和Xj之间的距离r可以计算如下:
(9)
式中:D—优化问题的维度。
对于每个萤火虫,其位置更新公式如下:
Xi(t+1)=Xi(t)+β(Xj(t)-Xi(t))+αεi
(10)
式中:εi—随机值。
由式(10)可知,FA中个体位置由3个因素决定:萤火虫个体当前所处的位置,对另一个萤火虫位置的可取性,以及随机数εi和随机因子α。
2.1.2 活性变异算子
区别于基本FA,ACFA在执行完基本FA的位置更新算子后增加最优粒子的局部搜索机制。设定1个变异概率Pa,随机生成1个0~1之间随机数rand,若rand>Pa,则对最优个体Xbest执行高斯扰动策略,以增强最优个体活性。该策略通过对最优解附近的解空间进行局部开发,可有效增强萤火虫算法的局部寻优能力。执行如下:
(11)
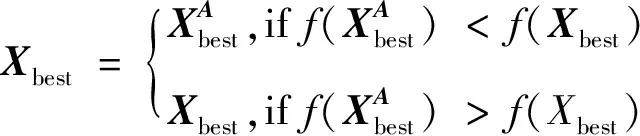
(12)

N(0,1)—服从标准正态分布的随机量。
2.1.3 概率维度竞争算子
与大多数智能算法相似,FA在寻优后期不可避免地会出现局部最优问题,而智能算法的局部最优往往是由待优化参数的某一维或某几维陷入局部最优解造成的,故为FA增加1个概率维度竞争算子。当FA的最优个体的适应度值连续10代保持不变时,则转而执行概率维度竞争算子,使算法顺利跳出局部最优。
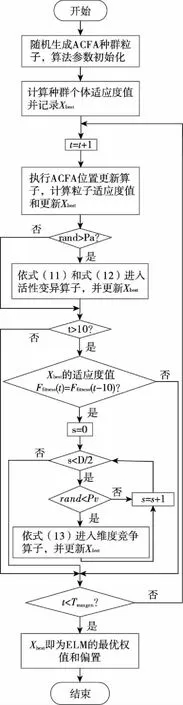
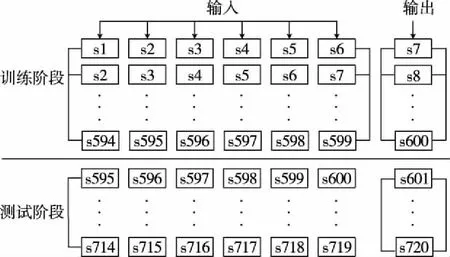
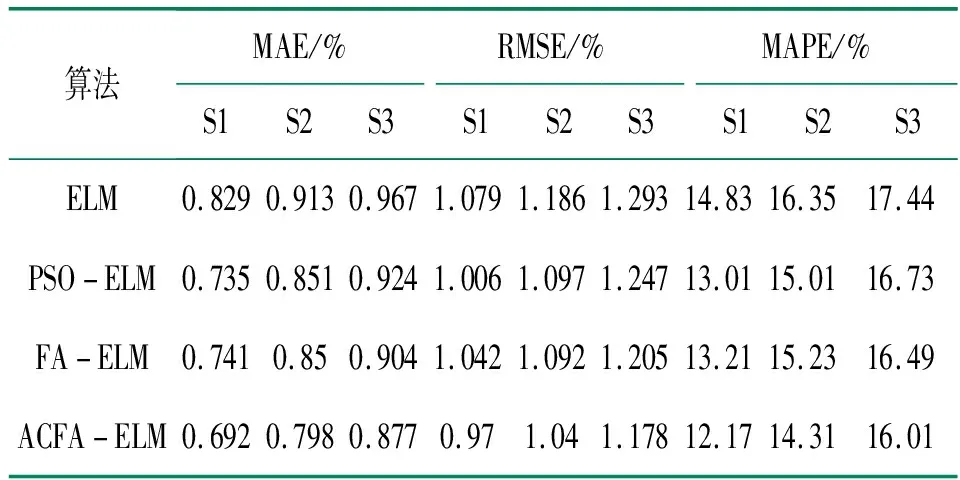
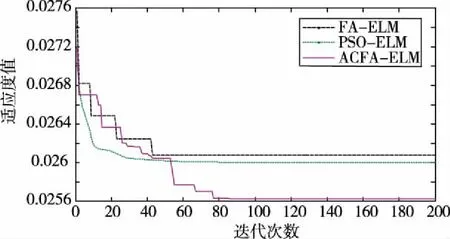
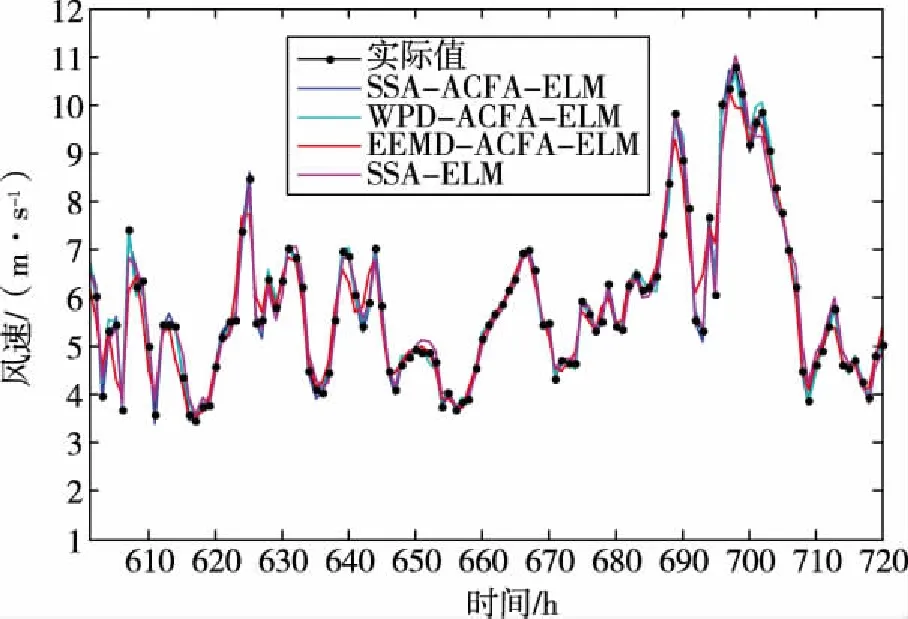
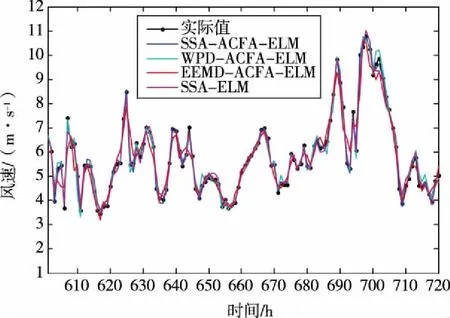
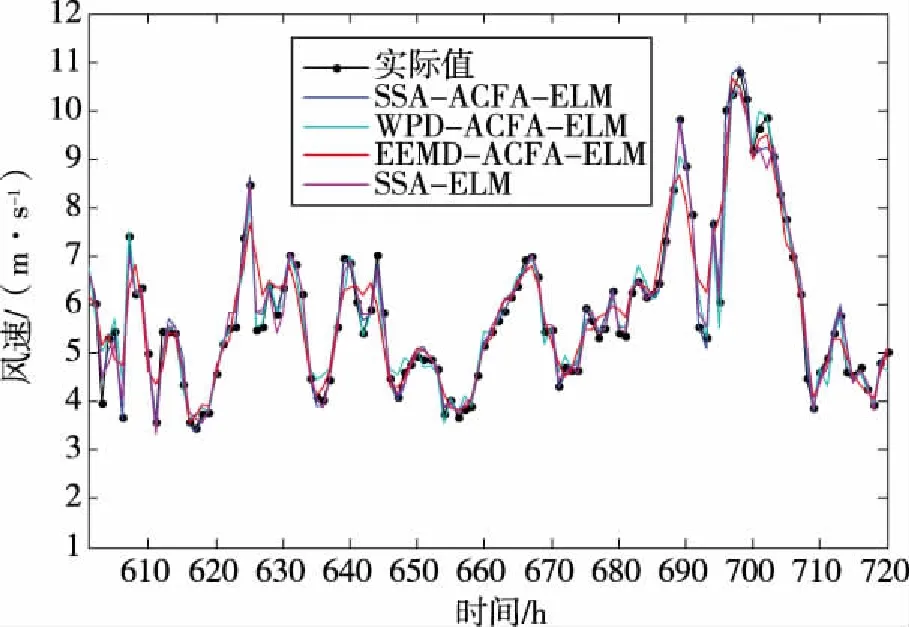
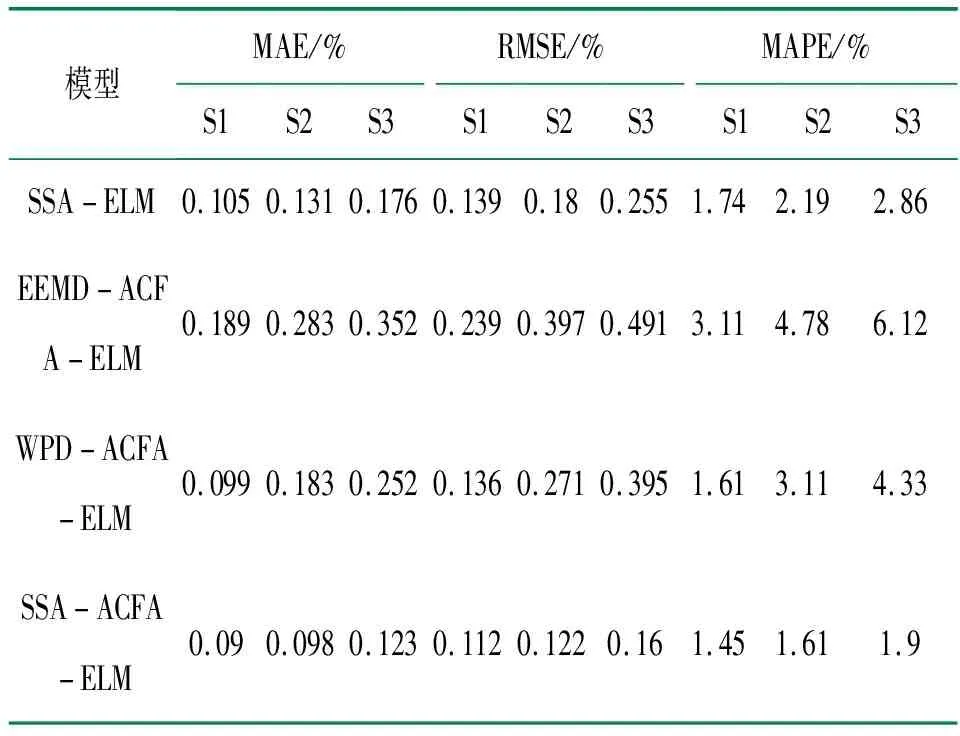
首先对种群中个体所有维(即所优化问题的维度D)进行两两不重复随机组合,共D/2对组合。根据每对组合,对种群中全部个体依维度竞争概率Pv执行维度竞争算子。假设(d1,d2)是其中的一对组合,对于个体X(i)的第d1维和第d2维,若rand Mvc(i,d1)=r·X(i,d1)+(1-r)·X(i,d2) (13) i∈N(1,M);d1,d2∈N(1,D);r∈[0,1] 式中:Mvc—折中解矩阵,用于保存概率维度竞争算子产生的新个体。 值得注意的是在执行完概率维度竞争算子后,需根据式(18)计算Mvc中所有个体的适应度函数值,并与X中对应的粒子进行适应度值竞争,以优胜劣汰原则保存适应度值更优的粒子,并更新Xbest。 (14) 式中:wi=[wi1,wi2,…,win]T—第i个隐含层神经元与n个输入神经元之间的连接权重矩阵; βi=[βi1,βi2,…,βim]T—第i个隐含层神经元与m个输出神经元的连接权重矩阵; bi—第i个隐含层神经元的偏置。 ELM的结构如图1所示。 图1 ELM的结构 上述等式的矩阵形式可以表示如下: Hβ=T (15) 式中:H—隐含层的输出矩阵; T—目标输出矩阵。 ELM的网络初始参数即输入权值和隐层偏置是随机生成,这些参数是介于0~1之间的随机数。由于ELM样本数据的输入和输出已经确定,若网络初始参数一经确定,则隐含层神经元的输出矩阵H就保持不变,通过式(17)计算ELM隐含层与输出层连接权重矩阵的过程即为模型的训练过程。 β=H+T (17) 式中:H+—隐含层神经元输出矩阵H的摩尔-彭罗斯(Moore-Penrose)广义逆矩阵。 由式(15)和(17)可知,ELM的网络初始参数决定了ELM的预测性能,ELM随机生成网络初始参数会导致非最优参数的问题,故为提升ELM的预测精度,降低网络参数选择的随机性对预测结果的影响,本文将所提ACFA用于ELM网络初始参数的优化。ACFA的适应度函数是预测误差的MSE,定义如下: (18) y(t)—实际值; N—训练集数据总数。 ACFA优化ELM的流程如图2所示。 图2 ACFA优化ELM的流程 (1)初始化ACFA的种群和参数。在ACFA算法中,包括最大迭代次数Tmaxgen,萤火虫数M,随机因子α,吸收系数γ,距离为0时的吸引度β0,活性变异概率Pa,维度竞争概率Pv。 (2)设置迭代变量,当前迭代次数t=t+1。 (3)根据当前萤火虫和其他萤火虫之间的距离,计算其他萤火虫荧光强度。 (4)根据荧光强度的吸引力,依据式(10)更新萤火虫位置,并使用公式(18)计算每个个体的适应度值,在每次迭代中找到适应度值最小的萤火虫,记为全局最优个体Xbest。 (5)进入活性变异算子,若rand>Pa,则根据式(11)和(12)对最优个体Xbest进行高斯变异,进入局部搜索,并更新Xbest,否则转6)。 (6)若t<10,则转(7);若t>10,则判断种群最优个体Xbest的适应度值是否连续10代保持不变,若Ffitness(t)=Ffitness(t-10),则进入概率维度竞争算子,根据维度交叉概率Pv和式(13)更新萤火虫个体位置,否则,转(7)。 (7)判断终止条件是否满足。如果当前迭代次数t大于Tmaxgen,则迭代终止,将Xbest转换为ELM的输入权值和隐层偏置,生成最佳的ACFA-ELM预测模型,否则转(2)进行新一轮迭代。 本文实验由2个部分组成:第一部分为算法性能比较;第二部分为预测模型对比分析。实验样本为西班牙(风电场1)和荷兰(风电场2)某风电场实际采集的风速数据,选取其中720个样本进行提前1步(S1)、2步(S2)和3步(S3)预测实验,以提前1步预测为例,训练样本集和测试样本集数据构成如图3所示。本文所有的训练和仿真均在matlab R2011b版本环境下进行, 采用宏基4750 G 2.3 GHz双核处理器,3.0 G内存计算机平台。 图3 训练样本集和测试样本集数据构成 为避免随机性对预测结果的影响,每次实验独立运行20次取平均值,采用平均绝对误差(mean absolute error,MAE)、平均绝对百分比误差(mean absolute percentage error,MAPE)和均方根误差(root of the mean squared error,RMSE)。 为验证本文所提ACFA算法的有效性,分别采用粒子群和基本FA算法优化ELM,以风电场1的数据作为实验样本,进行提前1步、2步和3步的预测实验,3种算法的最大迭代次数和种群大小保持一致,Tmaxgen= 200,M=30。其他参数设置如下:ACFA中α= 0.9,γ= 1,β0= 1.0,活性变异概率Pa为0.3,维度竞争概率Pv为0.5;FA参数与ACFA相同;PSO惯性权重设为0.4,加速因子设为2。其中,本文选择Sigmoid作为ELM模型的隐含层函数,隐含层神经元数量为6个。 不同算法的预测误差如表1所示,不同算法的1步预测最优收敛曲线如图4所示。 表1 风电场1中不同算法的预测误差 图4 不同算法的1步预测最优收敛曲线 由表1可知,FA-ELM和PSO-ELM在1到3步预测中各误差指标相差不大,1步和2步预测中PSO-ELM预测精度稍好,3步预测中FA-ELM的预测精度又略占优势,但同单一的ELM相比,FA-ELM和PSO-ELM均具有更高的预测精度,说明随机生成网络参数的方式在一定程度上限制了ELM预测性能的提升,而利用智能算法优化ELM参数,可有效降低随机初始参数对ELM的影响,优化得到最优的网络参数,提高模型预测精度;ACFA-ELM 1步到3步的MAPE较FA-ELM和PSO-ELM分别提高1.04%、0.92%、0.48%和0.84%、0.7%、0.72%,结合图4的算法收敛曲线可知,ACFA通过引入活性变异算子和概率维度竞争算子,有效增强了算法的全局收敛能力,算法迭代后期能收敛到更优质的全局最优值,最大程度提高了ELM的预测性能,所提ACFA优于基本的FA算法。 为说明模型的优越性,建立WPD-ACFA-ELM(即对原始风速序列进行小波包分解,对分解得到的各子序列建立ACFA优化ELM的预测模型)、EEMD-ACFA-ELM(即对原始风速序列进行集合经验模态分解,对分解得到的各分量建立ACFA优化ELM的预测模型)、SSA-ELM(即采用SSA对原始风速序列进行分解,对各分量直接采用ELM进行预测)。其中,WPD采用“sym6”小波进行3层分解;EEMD集合数N为300,添加白噪声的标准差设置为0.3;SSA仅需设置1个参数,即窗口长度L设为12。风电场1和风电场2中不同模型的预测误差分别如表2和表3所示。以风电场1为例,不同模型的1步、2步和3步最优预测曲线如图5-图7所示。 图5 不同模型的1步最优预测曲线 图6 不同模型的2步最优预测曲线 图7 不同模型的3步最优预测曲线 从表2和表3可以看出,4种模型中,SSA-ACFA-ELM预测模型在1步到3步预测中表现出最高的预测精度。对比基于SSA、WPD和EEMD 3种不同分解方式的模型可以看出:(1)基于SSA的预测模型的精度在风电场1和风电场2的多步预测中均优于其他2种分解方式,这主要是因为SSA的分解效果相对于WPD和EEMD更加优良,最大程度降低了风速的随机波动性对预测结果的影响,提高了预测模型的精度;(2)相对于SSA-ELM,SSA-ACFA-ELM的各项误差指标同样有一定程度的降低,再次说明采用ACFA优化ELM的参数,有效提高了ELM的预测性能,能够获得更优质的预测结果;(3)SSA-ACFA-ELM的3项误差指标较其他几种预测模型均有一定程度的降低,以风电场1为例,SSA-ACFA-ELM 1步到3步预测的MAPE较WPD-ACFA-ELM分别降低了33.3%、40.3%和42.3%,较EEMD-ACFA-ELM分别降低了66.5%、66.7%和63.4%,较SSA-ELM分别降低了23%、20.9%和27.5%,较单一的ELM分别降低了90.3%、88.2%和87.2%。各模型的对比可知,本文所提SSA-ACFA-ELM的预测精度在所有模型中表现最好,在风速多步预测中优于其他预测模型。 表2 风电场1中不同模型的预测误差 表3 风电场2中不同模型的预测误差 从图5-图7可以看出,4种模型都可大致预测出风速的未来变化趋势,但基于WPD和EEMD的预测模型在风速突变的拐点处预测效果不佳,在这些峰值处的预测值与实际值存在偏差,造成预测精度不高,而基于SSA的预测模型在这些拐点处则表现出优良的预测性能,其预测值与实际值更为接近,其内在原因在于SSA对风速的分解效果更佳,WPD次之,EEMD相对较差,所提SSA优于WPD和EEMD分解算法。 针对风速随机波动性强,难以准确预测的特点,将一种新颖的奇异谱分析用于风速序列分解,并结合极限学习机进行风速多步预测,且提出一种活性竞争萤火虫算法用于极限学习机的参数优化,算例分析表明: (1)所提ACFA算法较基本FA算法具有更强的全局搜索能力,有效克服了随机选择网络参数对ELM预测性能的影响,提高了ELM的预测精度。 (2)相对于WPD和EEMD,SSA更有效降低了风速自身波动性对预测结果的影响,有效提高了模型的预测精度。 (3)所提SSA-ACFA-ELM模型在风速多步预测中表现出较高的预测精度。2.2 极限学习机


2.3 极限学习机的参数优化步骤
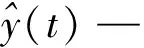
3 预测仿真实验
3.1 算法性能比较
3.2 模型预测效果对比分析

4 结 论

