各向异性电介质无界域泊松方程的定解问题

李文略

（岭南师范学院 基础教育学院，广东 湛江 524037）

陈燊年等系统研究了介质为各向异性（限于有且只有3个正交主轴方向的电介质）的电磁场，由各向异性电介质静电场的基本方程出发，导出静电势所满足的泊松方程，写出泊松方程的δ函数形式，并引进分离变量法研究各向异性电介质中有限域拉普拉斯方程的定解问题[1-2]。文献[3-8]由泊松方程出发，应用分离变量法、傅里叶变换法、格林函数法求解各向异性电介质有界域或无界域的定解问题。本研究拟由泊松方程的δ函数形式出发，应用联合积分变换法求解点电荷在无限大导体平面上方的各向异性电介质中激发的电势分布，以期为数学方法在各向异性电介质中无界域泊松方程定解问题研究中的应用提供补充。

1 各向异性电介质无界域泊松方程定解问题的确定

2 应用联合积分变换法求解无界域泊松方程的定解问题

泛定方程的等号右边计算为

第二类边界条件为

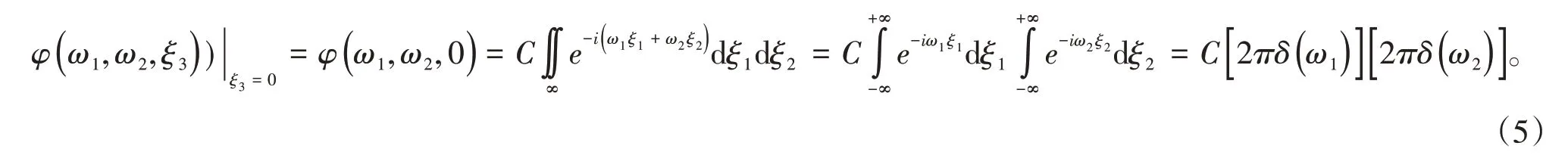
于是，式（2）写为

由求得的电势分布式（23）和（24）可知，电势分布是以分段的形式写出的，点电荷激发的电场线一部分会终止于导体的平面，另一部分会终止在x3→+∞的地方，电势分布结果符合判断预期。

3 结语

陈燊年等从各向异性电介质中静电场的3个基本方程出发，在引入静电势的基础上推导出各向异性电介质泊松方程的δ函数形式，但未对δ函数形式表示的泊松方程的应用作深入研究[1]。由本研究可知，各向异性电介质泊松方程的δ函数形式在研究各向异性电介质无界域泊松方程的定解问题时有很好的应用。将各向异性电介质主轴坐标系下泊松方程的定解问题式（1）通过变量代换转化为电各向异性坐标系下泊松方程的定解问题式（2）是研究中常用的技巧方法[1]；当无界域范围为( - ∞,+ ∞)和(0,+ ∞)或( - ∞,0)同时出现时，应用联合积分变换法能较好地求解该类无界域泊松方程的定解问题，由求得的结果式（23）、（24）亦可知，应用联合积分变化法求得的解往往是积分形式解，该解表示为傅里叶卷积或拉普拉斯卷积。